3D RECONSTRUCTION FROM LINE DRAWINGS

Lars H. Wendt

, Andr

e Stork

, Arjan Kuijper

and Dieter W. Fellner

Interactive Graphics Systems Group, TU Darmstadt, Germany

Fraunhofer Institute for Computer Graphics Research IGD, Darmstadt, Germany

Keywords:

Sketched-based modeling, Computer-aided design, 3D reconstruction.

Abstract:

In this work we introduce an approach for reconstructing digital 3D models from multiple perspective line

drawings. One major goal is to keep the required user interaction simple and at a minimum, while making no

constraints to the objects shape. Such a system provides a useful extension for digitalization of paper-based

styling concepts, which today is still a time consuming process.

In the presented method the line drawings are ﬁrst decomposed in curves assembling a network of curves. In

a second step, the positions for the endpoints of the curves are determined in 3D, using multiple sketches and

a virtual camera model given by the user. Then the shapes of the 3D curves between the reconstructed 3D

endpoints are inferred. This leads to a network of 3D curves, which can be used for ﬁrst visual evaluations

in 3D. During the whole process only little user interaction is needed, which only takes place in the pre- and

post-processing phases. The approach has been applied on multiple sketches and it is shown that the approach

creates plausible results within reasonable timing.

1 INTRODUCTION

Nowadays, digital 3D models are an important ele-

ment in design and engineering processes. They are

used for ﬁrst visual evaluations and later on they serve

as basis for Digital Mock-Ups or reﬁned CAD mod-

els. Nonetheless, in the ﬁrst phase of the product

development, style concepts still start with sketches

on paper. The problem of transferring those concepts

from paper to the digital world is not fully addressed

yet. During the styling phase a lot of sketches are cre-

ated from different objects and views. Though only

few of them are chosen for creating digital 3D models.

Creating these 3D models is complex and time con-

suming and therefore usually not done by the creator

of the sketch himself. Especially in companies where

styling is essential (e.g. in the automotive industry),

specially trained CAS (Computer Aided Styling) op-

erators create such ﬁrst 3D models. Beside the effort,

which is put in this step, the stylists intentions may

get lost.

We present a system, which a stylist can use with

little effort to create ﬁrst digital 3D models based on

multiple but few perspective 2D line drawings. The

system tolerates imprecision in the sketchy drawings

including perspective variances. To our knowledge

such a system does not yet exists.

Figure 1: Our proposed approach uses line drawings like

these of a couch for the reconstruction of 3D models.

That it is reasonable to constrain the sketch com-

plexity to line drawings is showed by (Tovey et al.,

2003). They decomposed sketches in their differ-

ent elements (form lines, components, form-shading,

non-form shading) and identiﬁed the form lines as

most important for transporting an idea of a shape.

Line drawings like in Figure 1 consist primarily of

those lines and therefore should be adequate for in-

ferring 3D shapes.

Even with reduced sketch complexity many chal-

lenges have to be faced:

• Working with non-predetermined views, for us-

ing sketches as they are;

• Handling perspective imprecision, because

sketches from the styling phase generally lack

H. Wendt L., Stork A., Kuijper A. and Fellner D. (2010).

3D RECONSTRUCTION FROM LINE DRAWINGS.

In Proceedings of the International Conference on Computer Graphics Theory and Applications, pages 65-71

DOI: 10.5220/0002818600650071

 SciTePress

perspective correctness;

• Line drawings of arbitrary freeform objects give

little geometric cues about shape;

• Little and simple user interaction, so the system

is useable by non experts with little effort;

• Handling ambiguity, which arise when inferring

3D information from 2D.

2 RELATED WORK

Extensive research is done in imitating sketching pro-

cesses to interactively create 3D models. A compre-

hensive overview and taxonomy of interactive sketch-

based modeling is given in (Olsen et al., 2008) and

(Olsen et al., 2009). These methods are excellent

for creating 3D models in an easy an intuitively way,

but they seldom address the use of prior created hand

drawn sketches.

Dealing with this (Kara et al., 2006) presented an

interactive method for transferring the shape infor-

mation from a sketch to a template model. For this

purpose a scanned image of a sketch from a non-

predetermined viewpoint is used. The Template is

then aligned with this image in an easy way by inter-

actively drawing the virtual bounding box of the ob-

ject. While redrawing the form lines of the sketch, the

shape is transferred onto the 3D template. In a newer

work Kara and Shimada (Kara and Shimada, 2008)

use ﬁducial points for aligning the template with the

sketch and for template deformation. Those ﬁducial

points are given by the user for the sketch and corre-

spond to ﬁducial nodes of the template. The above

mentioned approaches have the beneﬁt, that the user

does most of the interpretation and ﬁltering of the

strokes in the sketches. So the approach itself does

not need to cope with the heterogeneity of the input

sketches. While this is a promising and applicable

approach, in the end the user redraws his sketch.

In contrast more direct reconstruction need to

cope with the heterogeneity of input sketches and

3D models. This often results in making restrictions

to sketches and 3D models. One of the ﬁrst work,

which engages the direct reconstruction from a line

sketch was by Lipson and Shpitalni (Lipson and Sh-

pitalni, 1996). In their paper they present a method for

reconstructing a polyhedron from one orthographic

line drawing. The approach used geometric infor-

mation like parallelism and orthogonality of lines in

the sketches. This method is restricted to polyhe-

dra and does not support curved elements. (Varley

et al., 2004) propose a two stage approach where, the

user is asked to create a drawing of a curved object

and a corresponding polyhedron. In the ﬁrst stage

the polyhedron is reconstructed and serves as tem-

plate. In the second stage the edges and surface are

deformed to match the drawing of the curved object,

so that a curved object is reconstructed. A method for

elements with planar curves is presented in (Masry

and Lipson, 2005). In this paper ﬁrst the depths of

the vertices from the line drawing are determined by

checking the consistency with an underlying orthogo-

nal axis system. Planar curves are then reconstructed

by determining their plane equation by using an op-

timization function. According to the authors this al-

gorithm performs best on sketches that exhibit strong

orthogonal trends. Opposite to our approach, where

we not rely on orthogonality and aim for the recon-

struction of non-planar curves.

While the previous works used single views there

also exist approaches working with multiple sketches.

(Wang and Latif, 2003) proposed a method for in-

ferring a solid 3D model from engineering drawings,

therefore extruding 3D objects from the 2D sketches

and combining them using constructive solid geome-

try methods. Their approach is restricted to the or-

thographic front, side and top views. Zhang et al.

cover in (Zhang et al., 2004) the reconstruction of a

wireframe model consisting of conic curves. In their

work the views are restricted to the same three main

views. In contrast, we use perspective sketches from

arbitrary viewpoints.

Even though many different approaches for inter-

preting drawn sketches exist, to our knowledge, no

approach for reconstructing a 3D model, consisting

of curves, using perspective sketches with little user

interaction, has been presented so far.

3 OUR PROPOSED METHOD

We divide the reconstruction process into three main

stages (see also Figure 2). These stages will be cov-

ered more detailed in the following section.

The ﬁrst stage is vectorization. In this stage we

convert the raster image to a suitable 2D representa-

tion of the sketch, which then will be used for the re-

construction. In this vectorization stage we convert

off-line scanned images into a network of 2D curves,

which are linear approximated. We use a rather sim-

ple vectorization algorithm, because we support only

line drawings. The vectorization stage is covered in

Section 4.

The second one is the actual 3D reconstruc-

tion process where the 2D information from multiple

sketches is combined to infer a 3D wireframe model.

To receive a transformation from 2D sketch space to

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

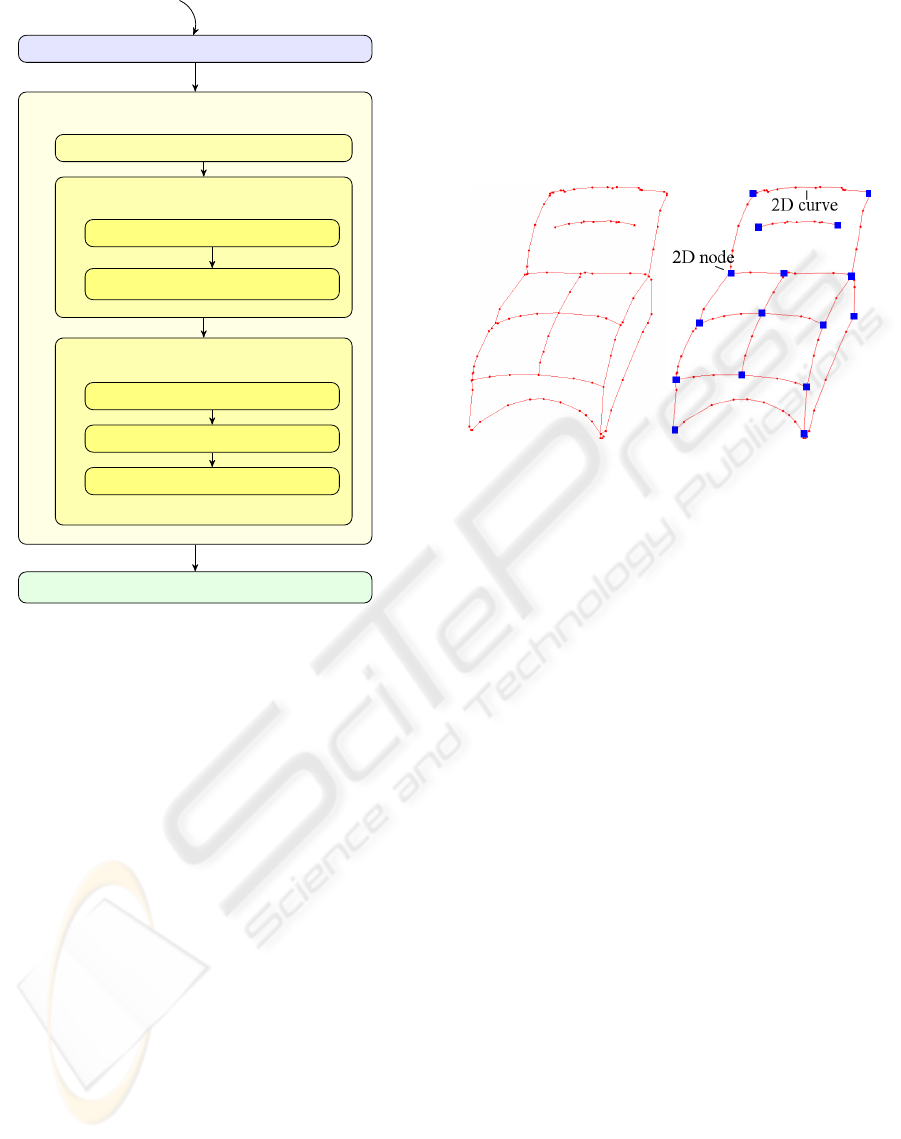
Vectorization

3D Reconstruction

Post-processing

2D network of curves

3D network of curves

Camera calibration

3D Node reconstruction

Shape reconstruction

3D edge graph

Generation of candidate nodes

Filtering of candidate nodes

Generation of 3D curves

Extrusion of 2D curves

Deformation of 3D curves

Sketches

Figure 2: Our proposed algorithm is divided in three main

stages.

3D object space we utilize a virtual camera model.

Then we determine the 3D positions to the endpoints

of the curves resulting from the vectorization. For the

transfer to 3D we are using the estimated projection

matrix from the camera model and the connectivity

information of the 2D network. In the following step

we deform the edges in 3D to the shape inferred from

their correspondent 2D curves. For this purpose we

divide the edge in 3D in a set of linear segments. The

forming is done by extruding the 2D curves into 3D

space, thus creating a surface on which the edge is

ﬁtted. Details are covered in Section 5.

The last stage is the post-process where the model

is visualized. The user has the possibility to modify

the model. Because we only reconstruct the visible

side of an object, the user can deﬁne a mirror plane to

extend symmetric objects. This is outlined in Section

4 VECTORIZATION

To get a suitable representation, the sketch is vector-

ized to a network of linear line segments (Figure 3).

This will be converted into a network of curves, where

the crossings of the drawn lines are the nodes and the

drawn lines the curves.

Figure 3: On the left: The vectorization result of the left

sketch from Figure 1. The drawn curves are approximated

polygonally. On the right: The 2D nodes from the network

of curves.

The vectorization algorithm we use is intended

for grayscale line drawings with roughly uniform line

thickness and without shading, like the two examples

shown in Figure 1. This is done with the following

image processing methods:

• First the image is converted to in a binary image

using an adaptive threshold algorithm, dividing

the raster image in foreground and background.

• With the morphological erosion operation we re-

move small artifacts created through the scan-

ning and binarization process. With the dilation

operation we close gaps between strokes.

• In a last step of morphological operations the

drawing is skeletonized. This means the lines

are thinned to a minimum while keeping the end

points.

• The skeleton, which results is now segmented in

polylines approximating the drawn curve.

• In the ﬁnal step we simplify the mesh by remov-

ing small dangling edges.

The vertices of the vectorization with a valency

higher or equal than three are considered as endpoints

of the curves. The path between two of these end-

points consist of linear edges and approximates the

drawn line polygonally. An example is shown in Fig-

ure 3. After this step the user can insert new nodes

and so additionally divide the curve. This is a use-

ful function, because in the following reconstruction

3D RECONSTRUCTION FROM LINE DRAWINGS

stage we receive better results when the topologies of

the networks of curves are similar.

5 3D RECONSTRUCTION

In the reconstruction stage we use multiple networks

of curves from the multiple sketches, for inferring a

network of 3D curves. This is done in three steps,

explained in the following sections.

5.1 Calibrating a Virtual Camera

For the calibration of a virtual camera model we pro-

ceed like previously described by Kara et al. in (Kara

et al., 2006). We ﬁrst need a set of pairs (at least 6) of

correlating 2D and 3D points. These points we get

by letting the user draw the projection of a virtual

bounding box into the sketch (see Figure 4). With

the eight corner points of the bounding box and the

approximate dimensions of the object (also given by

the user). We calculate an estimated projection ma-

trix from 3D to 2D, their inverse and the position of

the virtual camera.

Figure 4: This ﬁgure shows a bounding box given by a user -

the corners of this box are used to calibrate a virtual camera.

5.2 Reconstruction of Nodes in 3D

In this step we aim to reconstruct points in 3D, which

serve later as nodes of a network of 3D curves.

First we generate candidate nodes. A candidate

node is a node in 3D, which has the chance to become

the reconstruction of a 2D node. For the construc-

tion of those candidates, we divide the 3D space into

a voxelgrid. For each voxel of that grid, we calclulate

the 2D projection in the several sketches and deter-

mine the nearest 2D node. These 2D nodes are saved

on the voxel as witnesses, which means that this 2D

node could support the creation of a 3D node in this

voxel. After this we examine the voxels with two or

more witnesses. This implies that our algorithm needs

object nodes to be visible in more than one sketch.

Figure 5: This picture shows the 3D candidate nodes gen-

erated from the two sketches shown in Figure 1. The edges

visualize the candidates connectivity inferred from the net-

works of 2D curves.

Observing the voxelspace, we now see that clouds

of voxels have evolved. These voxel clouds contain

voxels which share the same set of witnesses. They

are compressed to their center creating a point in 3D.

This point is candidate to be the 3D representative of

its witnesses and so a candidate to be a 3D node of

the reconstruction. In Figure 5 we see the resulting

candidate nodes. An edge between two candidates in-

dicates that those two nodes have witnesses, which

are connected by a drawn curve in a sketch.

To ﬁlter the candidate nodes, we make use of the

connectivity information in the network of 2D curves.

The candidates are added to the resulting 3D network

by a greedy algorithm, which adds the nodes by a rat-

ing. The rating we applied here, reﬂects how well

a candidate is connected in the 3D network. There-

fore, we calculate the sums of lengths of all paths,

which starts at the 3D candidate node. These paths

travel over the neighbor candidates, while only using

candidates with at least two witnesses, which were

not witnesses of candidates prior on the path. Is a

candidate added to the 3D network, its witnesses are

removed from the witness list of the remaining can-

didates. Therefore it is necessary to recalculate the

rating after each addition of a candidate to the 3D net-

work.

This approach guaranties that a 3D node has only

one 2D representative per sketch and a 2D node has

only one 3D representative. So we resolved the am-

biguity by using the heuristic of connectivity of the

2D nodes. Now, we have a 3D wireframe model with

linear edges. The next step is to reconstruct the shape

information for these edges.

5.3 Shape Reconstruction

The main idea behind the shape reconstruction step

is to deform the edges in 3D in such a way that they

conform to the 2D sketch.

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

Figure 6: The candidate nodes are now ﬁltered and only the

edges between the resulting 3D nodes remain. The candi-

dates in the picture which are not connected to the network

are those which are discarded.

First we generate a 3D curve for each recon-

structed edge in 3D. Polylines serve as approximation

for the 3D curves. They are created by dividing an

edge in equally spaced linear segments.

We transfer the 2D shape information to 3D by ex-

truding a surface from the corresponding 2D curve.

We know the corresponding 2D curves for each 3D

curve from the reconstruction step of the 3D Nodes.

For extruding the surface we use the inverse of the

projection matrix from Section 5.1. With this matrix

we determine the rays from the virtual camera center

through the vertices of the 2D curve. These rays fan

the surface, like in Figure 7.

Then we deform the 3D curve by projecting the

vertices of the 3D curve onto this surface. For this

purpose we calculate for each 3D vertex a correspond-

ing interval on the 2D curve. Then the vertex is moved

to its nearest point on the part of the surface created

by the determined interval. This will allow us to adapt

extreme curves.

Figure 7: The extrusion of a 2D curve leads to a surface,

which is used for shaping the 3D curve.

Since we are working with multiple sketches more

than one corresponding curve exists. It seems sug-

Figure 8: An example for reconstructed 3D shape informa-

tion is shown. The marked curves will be deleted by the

user when he mirrors the object in the post-processing step

(see Section 6).

gestive to use the shape information of at least two

curves. This resolves ambiguity, because the 3D

curve is then well deﬁned by the intersection of two

extruded surfaces. We have implemented it by min-

imizing the distance of the 3D curve vertices to two

extruded surfaces. However, when the surfaces are

nearly parallel, the intersection prone to big devia-

tions in view direction. This is intensiﬁed by the in-

accuracy in the sketch and can lead to implausible

curves. In these cases best results were achieved by

using only one 2D curve. For this purpose, we want to

select the 2D curve which might give the best result.

So we use the longest 2D curve, under the assumption

that it contains better shape information than a shorter

one.

At this point we have a network of 3D curves like

the one showed in Figure 8.

6 POST-PROCESSING

The received 3D model from the previous section can

now be evaluated by the user. Many designed objects

are symmetric. Therefore, it seems sensible to give

the user at least the ability to extend the model by

adding the mirrored result. This gives the user a more

complete impression of the object. However, it can

lead to double curves, where curves are visible two

times in the sketch (e.g. on the near and the far side of

the object), like those marked in Figure 8. Some dou-

bled curves may be unwanted, stemming from impre-

cision or misinterpretation in the reconstruction. The

user has the possibilty to remove such curves at will.

3D RECONSTRUCTION FROM LINE DRAWINGS

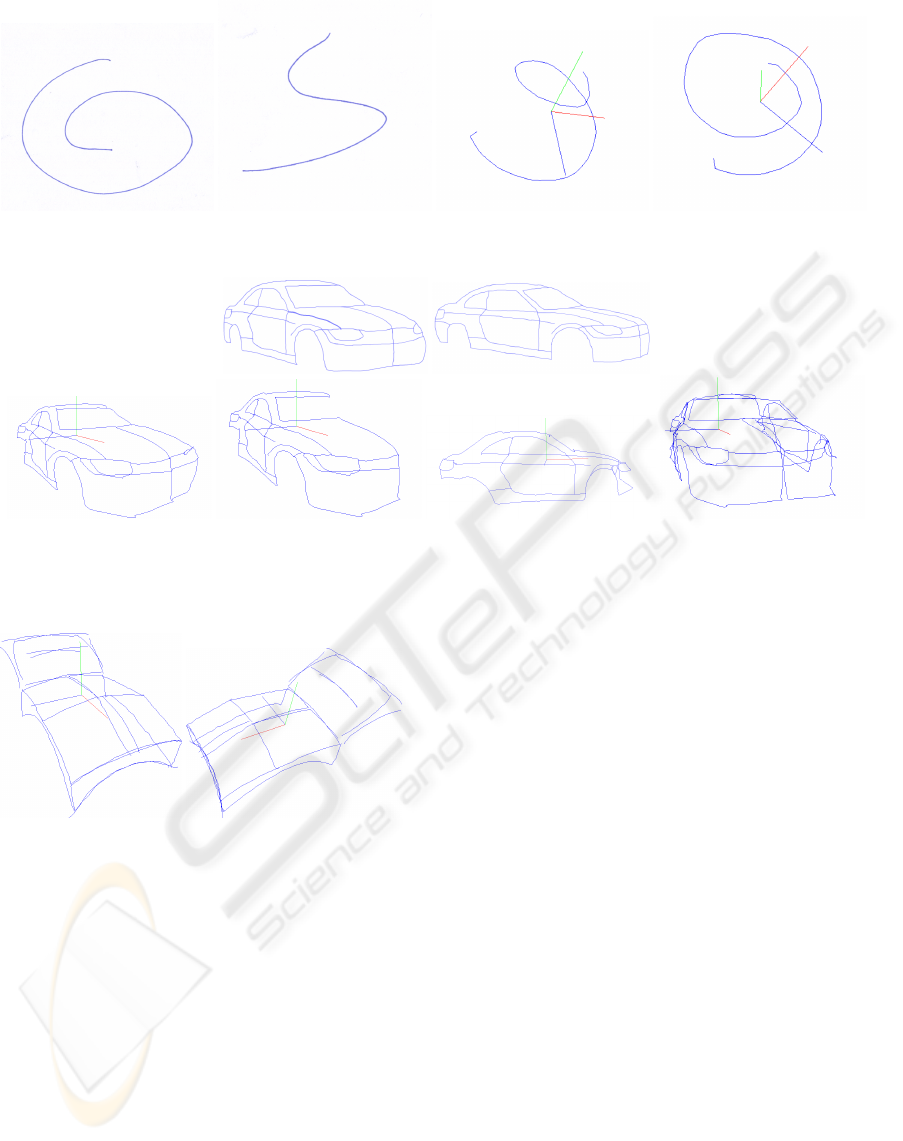
Figure 9: Result ”Spiral” a) Two line drawings of a 3D spiral on the left. One from top view the other from side view. b) The

reconstructed spiral in two views on the right. This shows that our method can reconstruct complex curves.

Figure 10: Result ”Car” a) Two line drawings of a car on top. b) On the left: The resulting 3D model with all reconstructed

and deformed edges. c) Second from left: the model without manually deleted edges as preparation for the mirroring. d)

Second from right: The side view on the model. e) On the right: A mirror plane was deﬁned to extend the model.

Figure 11: Two views of the ﬁnal result from the two

sketches shown in Figure 1 for the couch example.

7 RESULTS

We show the implementation results on sketches of

three different objects in Figures 11-10.

The couch example (result in Figure 11) accom-

panied us throughout the paper. It is a good example

for sketches that lack perspective precision. It also

contains a drawn line which is not connected to the

rest of the model but nonetheless has a plausible re-

construction. This example was mirrored in the post-

process and three curves (those marked in Figure 8)

were removed. In the pre-processing step four 2D

nodes where inserted in each sketch.

Another example - a sketch of a spiral (see Figure

9) - shows that our method is able to reconstruct non-

planar curves. This is true as long as the drawn curve

is not self-intersecting. On self-intersecting curves

our vectorization algorithm creates a 2D node which

makes a reconstruction more difﬁcult.

The reconstruction of a complex model is shown

by an example of a car (see Figure 10). Here the

user inserted 2D nodes on the contour leading to a

more suitable segmentation of the curve. Furthermore

in the post-processing step the user has removed the

edges on the farther side of the symmetry plane and

mirrored the object.

The reconstruction stage took for all models only

few (2-5) seconds on a stand-alone PC, without the

time needed for camera calibration. The time needed

for interaction varied from 2 minutes (spiral, couch)

to 5 minutes (car). These durations cover all the in-

teraction (camera calibration, insertion of 2D nodes,

mirroring, removing 3D curves). We believe that

these timings are fast enough to justify further explo-

ration of the approach in a productive styling envi-

ronment. An obvious next step is to add surface re-

construction out of the 3D curves e.g. through Coons

patches.

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

8 CONCLUSIONS AND FUTURE

WORK

We have shown an approach for reconstructing a

3D model existing of curves from multiple but few

sketches. Only little user interaction is needed and

takes place in a pre- and post-processing step. In

the automated reconstruction process, we assume that

parts of an object, which should be reconstructed, are

present in at least two views with the same level of de-

tail. The sketches used, are perspective and show the

object from different not predetermined viewpoints.

Here the chosen voxel-based approach allows us to

handle perspective imprecision of the sketches to a

certain degree.With such features this method could

be part of a system to evaluate ﬁrst styling concepts.

However we want to do more evaluations of the

system with regard to user effort and robustness. A

further object of special attention is handling silhou-

ette lines. Silhouettes in sketches convey important

shape information. However the handling is difﬁcult,

because they are varying from view to view. Another

focus of our future work is to utilize robust vector-

ization approaches like (Hilaire and Tombre, 2006)

so we can use sketches containing more complex-to-

handle content such as shading.

ACKNOWLEDGEMENTS

We want to thank the reviewers for helpful advises

and corrections. For the implementation of this work

we used the Open Source Libraries OpenCV, QGar

and OpenSG. This work is partially supported by the

European projects 3D-COFORM (FP7-ICT-2007.4.3-

231809) and FOCUS K3D (FP7-ICT-2007-214993).

REFERENCES

Hilaire, X. and Tombre, K. (2006). Robust and Accu-

rate Vectorization of Line Drawings. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

28(6):890–904.

Kara, L. B., D’Eramo, C. M., and Shimada, K. (2006). Pen-

based styling design of 3D geometry using concept

sketches and template models. In SPM ’06: Proceed-

ings of the 2006 ACM symposium on Solid and phys-

ical modeling, pages 149–160, New York, NY, USA.

ACM.

Kara, L. B. and Shimada, K. (2008). Supporting early

styling design of automobiles using sketch-based 3D

shape construction. Computer-Aided Design and Ap-

plications, 5(6):867–876.

Lipson, H. and Shpitalni, M. (1996). Optimization-based

reconstruction of a 3D object from a single freehand

line drawing. Computer-aided Design, 28(8):651–

663.

Masry, M. and Lipson, H. (2005). A Sketch-Based Interface

for Iterative Design and Analysis of 3D Objects . In

Jorge, J. A. P. and Igarashi, T., editors, Eurographics

Workshop on Sketch-Based Interfaces and Modeling,

pages 109–118, Dublin, Ireland. Eurographics Asso-

ciation.

Olsen, L., Samavati, F., Sousa, M. C., and Jorge, J. A.

(2009). Sketch-based modeling: A survey. Computers

& Graphics, 33(1):85–103.

Olsen, L., Samavati, F. F., Sousa, M. C., and Jorge, J.

(2008). A Taxonomy of Modeling Techniques using

Sketch-Based Interfaces . In Theoharis, T. and Dutre,

P., editors, Eurographics 2008 - State of the Art Re-

ports, pages 39–57, Crete, Greece. Eurographics As-

sociation.

Tovey, M., Newman, R., and Porter, S. (2003). Sketching,

concept development and automotive. Design studies,

24:135–153.

Varley, P. A. C., Takahashi, Y., Mitani, J., and Suzuki, H.

(2004). A Two-Stage Approach for Interpreting Line

Drawings of Curved Objects . In Jorge, J. A. P., Galin,

E., and Hughes, J. F., editors, Sketch-Based Interfaces

and Modeling, pages 117–126, Grenoble, France. Eu-

rographics Association.

Wang, Z. and Latif, M. (2003). Reconstruction of a 3D solid

model from orthographic projections. In Proceedings

of the 2003 International Conference on Geometric

Modeling and Graphics (CMAG’03), pages 75–82.

Zhang, A., Xue, Y., Sun, X., Hu, Y., Luo, Y., Wang, Y.,

Zhong, S., Wang, J., Tang, J., and Cai, G. (2004). Re-

construction of 3D curvilinear wireframe model from

2D orthographic views. In Computational Science -

ICCS 2004, volume 3037 of Lecture Notes in Com-

puter Science, pages 404–411. Springer Berlin / Hei-

delberg.

3D RECONSTRUCTION FROM LINE DRAWINGS