
RADIOMETRIC
RANGE IMAGE FILTERING FOR
TIME-OF-FLIGHT CAMERAS
Faisal Mufti and Robert Mahony
Faculty of Engineering and Information Technology, ANU, Australia
Keywords:
Time-of-flight camera (TOF), Reflectance model, Statistical analysis, Radiometric range criterion, Range fil-
tering.
Abstract:
Time-of-Flight (TOF) imaging devices provide distance measurements between the sensor and an observed
target over a full image array at video frame rate. An essential step in the development of these devices is an
understanding of the reliability of noisy range image data. This paper provides a unified frame work for TOF
camera measurement and a radiometric reflectance model. A statistical analysis of the radiometric model is
used to develop a range pixel reliability criterion to identify range errors. The radiometric model is verified
using real data and the proposed range criterion is experimentally verified.
1 INTRODUCTION
In recent years, the demand for 3D vision systems
has increased in a number of fields; such as; for ex-
ample, detection and recognition (Fardi et al., 2006),
3D environment reconstruction (Kuhnert and Stom-
mel, 2006) and tracking (Meier and Ade, 1997), etc.
This has lead to increase effort in the development
of range image technology and especially Time-of-
Flight (TOF) cameras (Lange and Seitz, 2001). In
general, 3D TOF cameras work on the principle of
measuring time of flight of a modulated infrared light
signal as phase offset after reflection and provide
frame rate range and intensity data over a full image
array at video frame rate (Kahlmann et al., 2007).
A key issue for TOF cameras is to evaluate the re-
liability of the range measurement from the received
signal in the presence of noise (Moller et al., 2005).
Noise due to systematic and statistical error is studied
under various calibration methods based on experi-
mental data acquired in a known environment (Kuhn-
ert and Stommel, 2006). Kahlmann et al. (Kahlmann
et al., 2006) characterized the cyclic deviation in dis-
tance measurement caused by uneven harmonics in
modulation. Calibration techniques using lookup ta-
bles (LUT) for effect of temperature, reflectivity of
the target and integration time on distance measure-
ment have also been studied (Kahlmann et al., 2007;
Radmer et al., 2008). Likewise, Lindner and Kolb
(Lindner and Kolb, 2006) proposed depth error cor-
rection based on perspective calibration and linear
adjustment but are constrained for high and low re-
flective surfaces that are closer to the camera or vice
versa. These calibration methods, however, require a
specific set of calibration experiments for each cam-
era, and the resulting calibration minimization is an
average approximation for each pixel.
The sensitivity of the distance measurement data
obtained in a Time-of-Flight (TOF) camera is highly
dependent on the signal-to-noise ratio (SNR) of ac-
tive light received by the sensor. Noisy range values
in a TOF camera are normally a result of a low inte-
gration time, a distant target or a signal received from
low reflective surface in the camera. Attenuation due
to distance is a result of classical inverse square law
of signal attenuation and is straightforward to model.
The link between integration time and noise of the re-
ceived signal has been considered (Kahlmann et al.,
2006). The effect of reflectivity on SNR, however,
is more complex to model. Reflectivity is a parame-
ter that depends on the observed scene (Lindner and
Kolb, 2007) pixel by pixel as illustrated in Figure 1.
Most real environment scenes consist of objects that
can be modelled as Lambertian surfaces (Cook and
Torrance, 1982). Since recovering reflectivity is a
common problem in Shape From Shading (SFS), the
reflectivity of Lambertian surfaces has been exten-
sively studied (Zhang et al., 1999) in computer vision.
Horn (Horn, 1977) approached this problem through
the introduction of reflectance map. Techniques based
on photometric stereo to recover surface albedo re-
quire multiple images or multiple sources to solve an
143
Mufti F. and Mahony R. (2010).
RADIOMETRIC RANGE IMAGE FILTERING FOR TIME-OF-FLIGHT CAMERAS.
In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 143-152
DOI: 10.5220/0002819601430152
Copyright
c
SciTePress

0
10
20
30
40
0
10
20
30
40
50
1.7
1.8
1.9
2
2.1
2.2
2.3
2.4
2.5
Distance in meters
(a)
(b)
Figure 1: Range data (a) obtained for the PMD 3ks TOF
camera imaging a flat board (b) pasted with nine low re-
flectivity patches. The SNR
db
varies from 44.4db (forwhite
board) to 7.3db (for the low reflective patches). The varia-
tion associated with low SNR is clearly visible in the range
error seen in (a).
ill-conditioned inverse problem (Zhou et al., 2007).
The complexity and the degree of error due to min-
imization algorithms (Zheng and Chellappa, 1991),
and imaging conditions (Zhang et al., 1999) limits the
applicability of reflectance modelling of environment
in computer vision applications. Reliability of signal
strength and range data in the presence of unknown
reflectivity is a significant challenge for TOF cameras
in real environments. To authors’ knowledge there is
little or no prior work to overcome TOF range mea-
surement error due to signal strength variation, inde-
pendent of scene reflectance.
This paper investigates the radiometric mod-
elling of TOF measurements and background light
sources by exploiting the dependencies between am-
plitude, intensity and range/phase measurements. We
consider statistical noise model of TOF measure-
ments, that along with radiometric properties of light
sources, and a Lambertian reflectance model enable
us derive a radiometric range model. Further in-depth
statistical analysis of parameters of this model is used
to formulate a radiometric range criterion. From this
criterion we can effectively evaluate pixel-by-pixel re-
liability of range measurement in TOF cameras that
is independent of scene reflectivity. For the purpose
of this conference paper, we restrict our attention to
the case of planar surfaces. The proposed reliability
criterion helps in evaluating and filtering TOF range
measurements under various SNR conditions, a key
parameter for radiometric range criterion.
The paper is organized as follows: Section 2 de-
scribes TOF signal measurement, Section 3 provides
statistical models for the measurements, Section 4 de-
scribes a reflectance model from TOF camera per-
spective and Section 5 presents a radiometric range
model. In Section 6 we provide statistical analysis of
radiometric range model, and then go on to propose a
range pixel reliability criterion in Section 7. Section
8 presents experimental results of the implementation,
and a short conclusion follows.
2 TIME-OF-FLIGHT SIGNAL
MEASUREMENT
Time-of-Flight (TOF) sensors estimate distance to a
target using the time of flight of a modulated in-
frared (IR) wave between the target and the cam-
era. The sensor illuminates/irradiates the scene with
a modulated signal of amplitude A (exitance) and re-
ceives back a signal (radiosity) after reflection from
the scene with background signal offset I
o
that in-
cludes non-modulated DC offset generated by TOF
camera as well as ambient light reflected from the
scene (see Figure 2).
There is a phase delay of the received modulated
signal proportional to the ratio of range on speed of
light of the observed point in the scene. The ampli-
A
o
A
1
D
t
time
= 20 MHz, T = 50 nsec
Signal strength
f
mod
mod
A
2
A
3
A
o
A
I
o
I
j
Figure 2: Received modulated signal in TOF camera. The
signal of modulated frequency f
mod
= 20Mhz with back-
ground illumination (exitance) I
o
, is sampled four times
A
o
,A
1
,A
2
,A
3
. These measurements are used to calculate
amplitude A (1), phase ϕ (2) and intensity I (3).
tude and phase of a modulated signal can be extracted
by demodulating the incoming signal A = A
i
cos(ωt
i
+
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
144

ϕ) + I; (t
i
= i ·
π
2ω
,i = 0,. ..3) (see Figure 2) by syn-
chronously sampling the received signal four times at
quarter wavelength intervals of the modulated source
frequency. The measured amplitude A, intensity I rep-
resenting the gray scale image and the phase of the
received signal are then respectively given by (Lange
and Seitz, 2001)
A :=
p
(A
3
−A
1
)
2
+ (A
0
−A
2
)
2
2
(1)
ϕ := arctan
µ
A
3
−A
1
A
0
−A
2
¶
. (2)
I :=
A
0
+ A
1
+ A
2
+ A
3
4
. (3)
With known phase ϕ, modulation frequency f
mod
and
precise knowledge of speed of light c, it is possible to
measure the un-ambiguous distance r from the cam-
era as
r := ϖϕ; where ϖ =
c
4π f
mod
. (4)
With a wavelength of λ =
1
f
mod
, this leads to a maxi-
mum possible unambiguous range of
λ
2
. For the PMD
3k-S TOF, the modulation frequency is 20MHz and
the maximum unambigiuos range is 7.5m.
3 STATISTICAL NOISES
MODELS OF THE
MEASUREMENTS
It has been shown (Lange and Seitz, 2001) that pho-
ton shot noise effects the optical measurement process
and is the major statistical noise process in TOF de-
vices. In (Mufti and Mahony, 2009), statistical mod-
els for amplitude, phase and intensity were proposed
that model the achievable signal-to-noise ratio (SNR)
of the sensor device.
The statistical distribution of amplitude is a Rice
distribution given by
ˇ
A ∼ Rice
³
A,
p
I/2
´
, (5)
where
ˇ
A denote the actual measurement obtained by
the TOF camera while A and I are the physical pa-
rameters of the model. The statistical distribution of
phase
ˇ
ϕ is given by
Φ(
ˇ
ϕ|A,ϕ,
p
I/2) =
1
2π
exp
µ
−
A
2
I
¶
h
1 +
A
√
I
cos(
ˇ
ϕ −ϕ)
(
√
π)exp
³
A
2
cos
2
(
ˇ
ϕ −ϕ)
I
´
n
1 + erf
³
A cos(
ˇ
ϕ −ϕ)
√
I
´oi
, (6)
where erf(.) is the error function. Here Φ is a
marginal distribution obtained by integrating over the
joint distribution function of a complex version of the
received signal (Bonny et al., 1996). The range mea-
surement can be related to phase measurement based
on the model (4) as
ˇr = ϖ
ˇ
ϕ. (7)
The statistical distribution for intensity is given by
(Mufti and Mahony, 2009)
ˇ
I ∼ N (I,I/4). (8)
The measurements
ˇ
A,
ˇ
I,
ˇ
ϕ, ˇr are thought of as the mea-
sured values of A,I,ϕ and r at pixel (x).
For a TOF camera a key performance parameter,
SNR is defined as (Lange and Seitz, 2001; B
¨
uttgen
et al., 2006; Mufti and Mahony, 2009)
SNR =
√
2A
√
I
. (9)
In (Mufti and Mahony, 2009), the relationship of
phase with SNR has been shown by noting the fact
that although the phase distribution (6) is written with
dependence on three parameters (A, ϕ,
p
I/2), in fact
only the ratio,
A
√
I/2
, appears on the right hand side in
the definition of (6). Consequently the phase distribu-
tion can be re-written as
ˇ
ϕ ∼ Φ
µ
ˇ
ϕ
A
A
,ϕ,
√
I
√
2A
¶
= Φ
µ
ˇ
ϕ 1, ϕ,
1
SNR
¶
. (10)
The model for SNR is a generic model for TOF
cameras (B
¨
uttgen et al., 2006). In practice manufac-
turers vary the configuration for customized designs
to improve performance in ways that do not funda-
mentally change the physics of the model but leads to
scaling effects that must be modelled. This process
for raw measurements is discussed in (Luan, 2001;
Mufti and Mahony, 2009) and is not further consid-
ered in this paper, although these effects must be un-
derstood to obtain experimental results.
We define a second key statistical factor for per-
formance measurement in TOF camera as signal-to-
offset ratio (SOR) of photon count. This ratio reflects
the total offset in the received signal with respect to
the amplitude of the modulated source and is given
by
SOR =
³
received signal amplitude
value of the background offset
´
=
³
A
I
o
´
. (11)
RADIOMETRIC RANGE IMAGE FILTERING FOR TIME-OF-FLIGHT CAMERAS
145
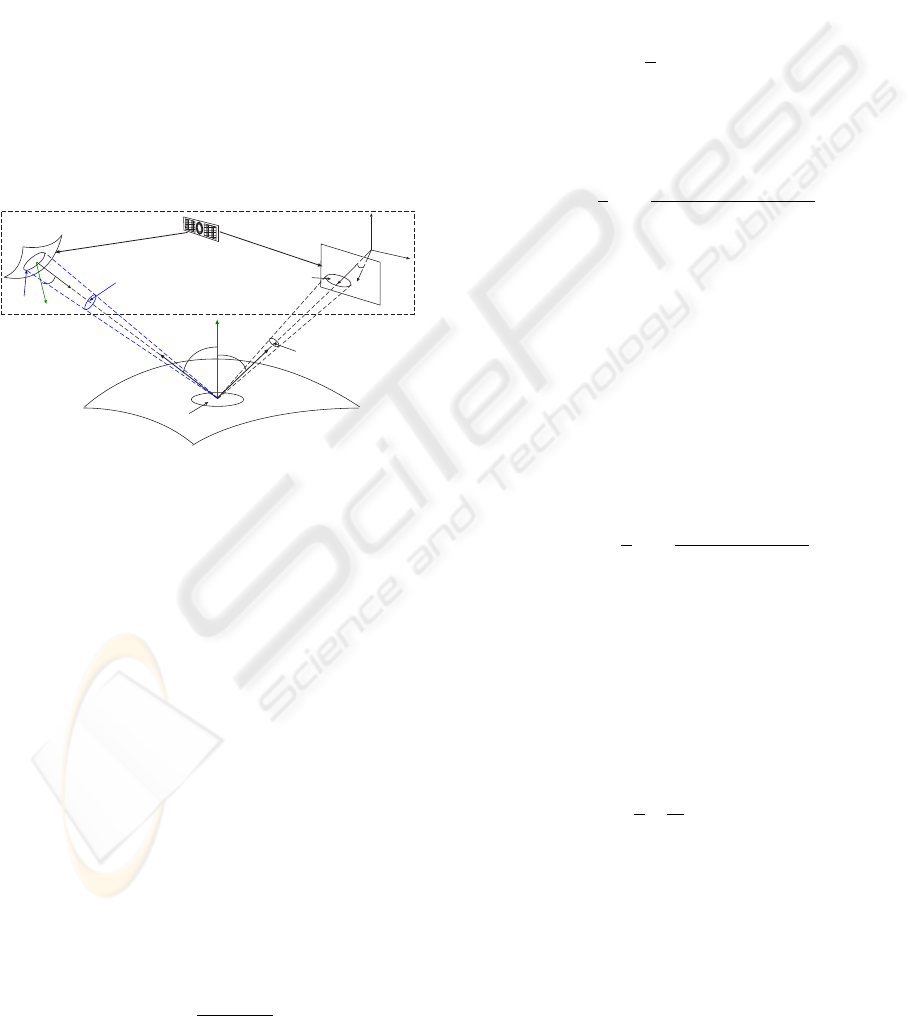
4 REFLECTANCE MODEL
The active signal of a TOF camera can be used for
measurement of amplitude A, intensity I, and range
r. These measurement parameters are not indepen-
dent but depend on the reflectance characteristics of
the scene. In order to develop reliability criteria for
TOF data it is necessary to provide background the-
ory for a reflectance model for time-of-flight (TOF)
camera and understand the signal behavior in a radio-
metric framework.
A reflectance model gives a relationship for light
emitted and received between a source, a surface and
the observer or the camera image plane. We consider
a near-field IR point source for the camera’s active
LED array and a far-field source for background illu-
mination.
n
p
S
P
dA
p
dA
s
dA
x
x
z
x
y
a
q
n
s
q
s
dw
p
qp
p
s
r
o
dw
x
p
TOF camera
Transmitter and receiver in same housing
Figure 3: Geometry of reflectance model for Time-of-
Camera. Note that although the source and receiver of a
physical TOF camera are co-located, it is difficult to pro-
vide a visualization of this geometry. Here the source is
shown separately to make is easier to see notation, however,
in practice the directional vectors r and x
p
are equal.
4.1 Reflectance Model for an IR Source
of TOF Camera
The primary source of illumination in TOF cameras
is an IR source that produces a modulated IR signal
offset by a non-modulated DC signal. The reflectance
model takes into account the modulated signal
represented by A(s) as well as the non-modulated DC
signal represented by I
c
(s).
Modulated IR Source. Let P be a Lambertian surface
in space with n
p
the normal to the each point p ∈ P
on the surface as shown in Figure 3. Let a modulating
IR point source S is irradiating the surface P then dω
denote the solid angle of dA
s
seen from point p. Then
dω =
cosθ
s
dA
s
r
2
, (12)
where θ
s
is the angle between the normal to the
source point s ∈ S and the ray of the modulated IR
signal reaching point p, and r is the distance between
source and the point p. Following the laws of radiom-
etry (Sillion and Puech, 1994) the amplitude of total
radiance A(p) (called radiosity) leaving point p due
to illumination by the modulated signal A(s) is pro-
portional to the diffuse reflectance or albedo ρ(p) and
the integral of irradiance over all the possible incom-
ing directions in a hemisphere, Ω, scaled by the cosine
of arrival angle θ
p
(Ma et al., 2003) (p. 68)
A(p) =
Z
Ω
1
π
ρ(p)A(s)cos θ
p
dω. (13)
By substituting (12) into (13) and changing the do-
main of integration to the surface, S, of the source
(Forsyth and Ponce, 2003) (p. 77), one has
A(p) =
Z
S
1
π
ρ(p)
A(s)cos θ
p
cosθ
s
dA
s
r
2
. (14)
An active TOF camera senses the received modulated
IR signal within its field of view and all the points
on surface illuminated by the camera can observe the
same source. In the present analysis, the LED point
sources of the camera are part of the compact IR ar-
ray of the TOF camera, and can be approximated by
a single virtual modulated point source (Forsyth and
Ponce, 2003, p. 78) with the center of illumination
aligned with the center of projection and the optical
axis of the camera (Kuhnert and Stommel, 2006). In
this case, the integration (14) can be re-written as a
function of the exitance of a single point source as
A(p) :=
1
π
ρ(p)
A(s)cos θ
p
cosθ
s
r
2
. (15)
Using the thin lens assumption, irradiance on an
image plane can be expressed by measuring the ra-
diosity along the direction x that depends on the ge-
ometry of the lens capturing the light (Ma et al., 2003,
p. 48) as
A(x) = ϒA(p). (16)
Here ϒ is the lens collection representing irradiance
fall-off with cosine-fourth law (Horn, 1986) (p. 208)
as
ϒ =
π
4
µ
d
f
0
¶
2
cos
4
θ
x
, (17)
where d is the diameter of the lens, f
0
is the focal
length of the lens and θ
x
is the angle of the ray from
the principle axis.
Non-modulated IR Source. The TOF camera
IR source produces a DC signal from the same IR
source LEDs. This signal will have the same re-
flectance model as has been derived for the modulated
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
146

IR source (see (15)). One has
I
c
(p) :=
1
π
ρ(p)
I
c
(s)cos θ
p
cosθ
s
r
2
, (18)
where the received signal I
c
(x) is given by
I
c
(x) = ϒI
c
(p). (19)
The effect of this signal is an added offset to the mod-
ulated signal for better illumination of the scene.
4.2 Reflectance Model for Background
Illumination
We also consider the background illumination of
the scene due to ambient light in TOF camera. In
computer vision (Alldrin et al., 2008) and computer
graphics (Cook and Torrance, 1982), a single view
point source of local shading model and an ambient
illumination model is generally preferred and we
would restrict our attention to these two models of
background illumination.
Ambient Background Illumination. Consider
an ambient background illumination of the scene i.e
an illumination that is constant for the environment
and produces a diffuse uniform lighting over the
object (Foley et al., 1997) (p. 723). Let I
a
be the in-
tensity (called exitance) of the ambient illumination,
then the received intensity I
a
(p) from a point p is
expressed as
I
a
(p) =
1
π
ρ(p)I
a
, (20)
where ρ, is the ambient reflection coefficient of a sur-
face. The irradiance on the image plane is given by
I
a
(x) = ϒI
a
(p). (21)
Far Field Background Illumination. For real envi-
ronments we also consider far-field point sources. For
a point source that is far away as compared to the area
of the target surface, the exitance does not depend on
the distance from the source or the direction in which
the light is emitted (Forsyth and Ponce, 2003) (p. 76).
The radiosity of point p due a point source q ∈ Q,
defined as I
b
(p), can be obtained by integrating each
of the sources as
I
b
(p) =
1
π
ρ(p)
Z
Q
I
b
(q)cos θ
q
dA
Q
, (22)
where θ
q
is the angle between normal to the surface
point p and the source point q, ρ(p) is the surface
albedo at point p and dA
Q
is the infinitesimal area of
a source Q. Considering a single IR far-field back-
ground point source of illumination, the radiosity per-
ceived by TOF image plane due to this IR source is
given as
I
b
(x) = ϒI
b
(p). (23)
where
I
b
(p) =
1
π
ρ(p)I
b
(q)cos θ
q
. (24)
5 RADIOMETRIC RANGE
MODEL
In Section 4, we derived the reflectance model for the
signal received by TOF camera. The perceived ra-
diosity for each pixel x is highly dependent on the
unknown diffuse reflectance ρ(p) (see (15), (18), (20)
and (24)). The value of this parameter ranges between
0 and 1. The received signal can have large fluctua-
tions corresponding to a different reflectivity of differ-
ent points p in the scene observed at pixel x. As a con-
sequence, there is a significant deviation in statistical
distribution of distance measurements for TOF cam-
era for different reflective surfaces (Lindner and Kolb,
2007; Mufti and Mahony, 2009). The received signal
obtained after reflection from object with very low re-
flectivity will lie in a region of low SNR. In 2D cam-
eras the only available measurement is intensity and
photometric stereo techniques are used to estimate re-
flectivity from multiple images or light orientations
to solve the associated under-determined system. A
TOF camera, however, measures amplitude, intensity
and phase. Hence, it is possible to create a unified
reflectance model based on all the available measure-
ment parameters that is robust against limitation of
unknown reflectivity.
From the basic principles of TOF camera signals
shown in Figure 1, we know that the intensity compo-
nent of TOF carries information for both, amplitude
of the modulated signal and the background offset I
o
.
Thus, we can represent the mean offset represented by
intensity of TOF cameras as
I := A + I
o
. (25)
The background offset I
o
is composed of DC offset
due to TOF camera I
c
and background illumination I
a
and I
b
depending upon the environment where TOF
camera is operating. One has
I
o
= I
c
+ I
a
+ I
b
. (26)
Indexing the point p in the scene by the TOF receiv-
ing pixel x and dividing (25) by A(x) and substituting
(26), one obtains
I(x)
A(x)
= 1 +
I
c
(x)
A(x)
+
I
a
(x)
A(x)
+
I
b
(x)
A(x)
. (27)
RADIOMETRIC RANGE IMAGE FILTERING FOR TIME-OF-FLIGHT CAMERAS
147

Using the local shading model for IR signal and the
background illumination of point sources (16), (19),
(21) and (23), one can re-write (27) as
I(x)
A(x)
= 1 +
I
c
(s)
A(s)
+
I
a
r
2
(x)
A(s)cosθ
p
cosθ
s
+
I
b
(q)cosθ
q
r
2
(x)
A(s)cosθ
p
cosθ
s
,
(28)
where θ
s
:= θ
s
(x) is a function of pixel.
The ratio of background ambient light I
a
to mod-
ulated TOF IR source A(s) can be defined as
κ
a
:=
I
a
A(s)
. (29)
Observe that κ
a
does not depend upon scene or cam-
era geometry and hence is a constant parameter over
the full image array. Similarly, define
κ
b
:=
I
b
(q)
A(s)
, (30)
as the ratio of far-field illumination and the TOF IR
source. The parameter κ
b
is once again a constant pa-
rameter independent of scene or pixel coordinates. Fi-
nally we define κ
c
as the ratio of TOF non-modulated
IR source I
c
(s) and TOF modulated IR source A(s)
κ
c
:=
I
c
(s)
A(s)
, (31)
Since the two sources of illumination originate from
the same IR LED source, any surface in the scene
will receive same amount of modulated and non-
modulated TOF IR source due to identical angle of
illumination. Thus we can redefine (31)
κ
c
(x) :=
I
c
(
x
)
A(x)
. (32)
where κ
c
(x) is function of a pixel x ∈R
2
and is a cam-
era based pixel parameter for an entire image. In the-
ory κ
c
(x) = κ
c
for all x that varies with the integra-
tion time. However, in practice slight variation in the
CMOS circuitry causes pixel variation in κ
c
(x) and is
modelled using calibration techniques documented in
Section 6.
The parameters (κ
a
,κ
b
) are constant over the im-
age plane. For any surface patch
1
, it is possible to
numerically compute an estimate of the angle θ
p
(x)
from the set of range measurements r(x
i
) associated
with that patch based on an estimate of the normal
vector to the surface (Pulli and Pietikainen, 1993;
Klasing et al., 2009; Ye and Hedge, 2009). For the
far field source we add two parameters (θ
az
,θ
el
) that
describe its azimuth and elevation with respect to the
camera frame. Given the estimate θ
az
,θ
el
then it is
1
The surface patch must be sufficiently large to be im-
aged by a small window of pixels.
also straightforward to compute θ
q
(x). We think of
these angles as functions of range data from pixels
corresponding to a local surface around a point in the
image. That is, denoting the local neighbourhood of x
by {x
i
}
n
i=1
used in the calculation of normal to x, one
has
θ
p
(x) := F
θ
p
[r(x
1
),··· ,r(x
n
)] (33)
θ
q
(x) := F
θ
q
[r(x
1
),··· ,r(x
n
),θ
az
,θ
el
]. (34)
Although the present spatial resolution of TOF cam-
eras have significant limitations, it is clear that future
technology will lead to TOF cameras with potentially
much higher resolution, making this process highly
effective.
Thus, using the parameters (κ
a
,κ
b
,κ
c
,θ
az
,θ
el
) of
sources one obtains a radiometric relationship as
I(x)
A(x)
= 1 + κ
c
(x) + κ
a
r
2
(x)
cosθ
p
cosθ
s
+ κ
b
cosθ
q
r
2
(x)
cosθ
p
cosθ
s
.
(35)
The above radiometric relationship is independent of
reflectivity ρ(p) and relate the measurable variables
A,I,r to constant parameters κ
a
,κ
b
,κ
c
and θ
az
,θ
el
.
5.1 Radiometric Range Model for
Planar Case
In this paper, we will only consider the case of ra-
diometric range model for planar surfaces using (35).
Consider the case of a single planar surface in the field
of view of TOF camera. Over this single surface it can
be easily seen that θ
q
is constant while θ
p
is nearly
constant for a small field of view of TOF optical sen-
sor over the surface. As a result several parameters
can be combined into a single constant. We propose
an approximate model
I(x)
A(x)
= 1 + κ
c
(x) + κ
o
r
2
(x)
cosθ
s
, (36)
where
κ
o
:=
κ
a
cosθ
p
+
κ
b
cosθ
q
cosθ
p
= constant. (37)
As a consequence of (37), a pixel measurement of κ
o
is given by
κ
o
(x) =
µ
I(x)
A(x)
−κ
c
(x) −1
¶
cosθ
s
r
2
(x)
. (38)
We will use κ
o
(x) as a radiometric criterion for range
reliability.
In practice the measurement of κ
o
(x) is a noisy
process due to noise in the statistical distribution of
measurement obtained. In the next section we provide
a detailed analysis of statistical distributions of κ
o
(x)
and parameters associated with it due to the noise in
the measurement process.
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
148

6 STATISTICAL DISTRIBUTION
OF
ˇ
κ
o
(x)
We have seen that κ
o
is a function of constant sources
(camera source and the background source of illumi-
nation) that cannot be directly measured in practice.
The relationship (38) provides a mean to measure κ
o
in practice. A statistical analysis of the measurement
of κ
o
(x) in this section will provide a significant in-
sight into radiometric range model for the planar case.
Consider a pixel x in the TOF image array and de-
fine the measurement
ˇ
κ
o
(x) as
ˇ
κ
o
(x) :=
µ
ˇ
I
ˇ
A
−
ˆ
κ
c
−1
¶
cosθ
s
ˇr
2
, (39)
where
ˆ
κ
c
is an estimate of camera based parameter for
an entire image. A
ˇ
κ
o
(x) is complex statistical distri-
bution composed of ratio of different distribution and
as such a closed form analytic solution is not possible.
However, based on the distributions of measurements
ˇ
A,
ˇ
I, ˇr and the estimate of
ˆ
κ
c
, we can represent the sta-
tistical distribution of
ˇ
κ
o
(x) in terms of independent
parameters. The statistical distributions of
ˇ
A,
ˇ
I and ˇr
have been discussed in Section 3.
The ratio of modulated and non-modulated IR
source of TOF camera, κ
c
(x), is fixed for each pixel
and is determined as a pre-processing step in TOF ra-
diometric range estimation. The estimation of κ
c
(x)
defined as
ˆ
κ
c
is a measurement process over a large
data set. For sufficient samples central limit theorem
ensures that,
ˆ
κ
c
∼ N
µ
κ
c
(x),
1
N
σ
2
[κ
c
(x)]
¶
. (40)
By knowing the distribution of dependent param-
eters we can now show that
ˇ
κ
o
(x) is sampled from
a distribution with three pixel based independent
parameters SNR, SOR and κ
o
. The two parameters κ
c
and θ
s
are camera parameters that can be calibrated in
the initial setup of the camera and are not considered
parameters of the distribution.
Lemma 1:
ˇ
κ
o
(x) Distribution Parameters.
Assume the camera parameters κ
c
(x) and θ
s
are
known and
ˇ
A(x), ˇr(x),
ˇ
I(x) are given by (5),(7) and
(8). Then the measurement
ˇ
κ
o
(x) =
µ
ˇ
I(x)
ˇ
A(x)
−κ
c
(x) −1
¶
cosθ
s
ˇr
2
(x)
, (41)
can be modelled as a random variable with distri-
bution depending on three independent parameters
SNR (9), SOR (11) and κ
o
(37).
Proof: Recall that A(x),I(x) and r(x) are the
underlying radiometric parameters of the ideal re-
ceived signal based on noise free radiometric model.
For ease of notation we drop the (x) dependence such
that A = A(x), I = I(x). Using the definition of SOR
(11) and (26), one can write
1
SOR
=
I
a
+ I
b
+ I
c
A
. (42)
Using (37), one has
κ
o
=
1
A(s)cos θ
p
(I
a
+ I
b
(q)cos θ
q
). (43)
Define new scaled measurement
¯
A :=
ˇ
A/A and
¯
I :=
ˇ
I/A then it is straight forward to verify from (5) and
(8) that
¯
A =
ˇ
A
A
∼ Rice
Ã
A
A
,
√
I
√
2A
!
= Rice
µ
1,
1
SNR
¶
(44)
¯
I =
ˇ
I
A
∼ N
µ
I
o
+ A
A
,
I
4A
2
¶
= N
µ
1 + SOR
SOR
,
1
2 ·SNR
2
¶
(45)
Using the radiometric model (16) for the true
range r, one has
r
2
=
ϒρ(p)
π
A(s)cos θ
p
cosθ
s
A
=
ϒρ(p)
π
A(s)cos θ
p
cosθ
s
A
(I
a
+ I
b
(q)cos θ
q
)
(I
a
+ I
b
(q)cos θ
q
)
= cosθ
s
µ
A(s)cos θ
p
I
a
+ I
b
(q)cos θ
q
¶
I
a
+ I
b
A
. (46)
Substituting (42) and (43), we obtain
r
2
=
cosθ
s
κ
o
µ
1
SOR
−κ
c
¶
. (47)
As a consequence of (4) one can write the true phase
as
ϕ :=
1
ϖ
s
cosθ
s
κ
o
µ
1
SOR
−κ
c
¶
(48)
Hence, using (7) and (10) we have shown
ˇr ∼
1
ϖ
Φ
µ
ˇr
ϖ
1,
s
cosθ
s
κ
o
·
1
SOR
−κ
c
¸
,
1
SNR
¶
. (49)
This shows that ˇr is a random variable with param-
eters SNR, SOR and κ
o
. From (41), using (44),(45)
and (49) one has
ˇ
κ
o
(x) =
µ
¯
I
¯
A
−κ
c
−1
¶
cosθ
s
ˇr
2
. (50)
Thus, the expression for
ˇ
κ
o
(x) is a function of random
variables
¯
A,
¯
I and ˇr. The random variables depend in
RADIOMETRIC RANGE IMAGE FILTERING FOR TIME-OF-FLIGHT CAMERAS
149

turn on the parameters SNR, SOR and κ
o
(44),(45)
and (49). Consequently,
ˇ
κ
o
(x) is a random variable
depending on parameters SNR, SOR and κ
o
.
¥
Let f
x
denote the distribution function for
ˇ
κ
o
(x). That
is
ˇ
κ
o
(x) ∼ f
x
(
ˇ
κ
o
(x)|SNR,SOR,κ
o
). (51)
The SNR is the dominant parameter of
ˇ
κ
o
(x) distribu-
tion due to the shot noise associated with Poisson ar-
rival process of photons of TOF signal and effects the
spread or tail of
ˇ
κ
o
(x) distribution. The parameters
SOR and κ
o
effect the mean value of the distribution.
0 10 20 30 40 50
0
0.02
0.04
0.06
0.08
0.1
0.12
Probaility density fucntion P(˘κ
o
)
˘κ
o
MC simulation
PMD data
Figure 4:
ˇ
κ
o
(x) Plot for Monte Carlo simulation and
real data from PMD camera (SNR
db
=12.14db, SOR
db
=-
38.61db, κ
o
=8.39).
It appears to be extremely difficult to derive an an-
alytic expression for the distribution of
ˇ
κ
o
(x). We
verify the model using Mote Carlo simulation with
model parameters A,I and ϕ to plot
ˇ
κ
o
(x) distribu-
tions (with parameters SNR, SOR, and κ
o
). A low
SNR case is plotted in Figure 4. The measured range
variation for this case is between 1.95m to 3.82m. The
simulation data matches with the experimental data,
confirming the validity of the proposed model param-
eters.
7 RADIOMETRIC RANGE
CRITERION FOR PIXEL
RELIABILITY
In this Section, we propose an algorithm for radio-
metric range filtering. The statistical analysis of
ˇ
κ
o
(x)
distribution (51) lead us to formulate a reliability cri-
teria based on a statistical test for
ˇ
κ
o
(x). That is given
estimates
d
SNR(x),
d
SOR(x) and
ˆ
κ
o
(x) of parameters
SNR, SOR and κ
o
at pixel x, let α > 0 significance
level, choose m(x) such that
P
f
x
h
(
ˇ
κ
o
(x) < m(x))|
d
SNR(x),
d
SOR(x),
ˆ
κ
o
(x)
i
= α,
(52)
where
Z
∞
m(x)
f
x
[
ˇ
κ|
d
SNR(x),
d
SOR(x),
ˆ
κ
o
(x)]d
ˇ
κ = α. (53)
Then,
ˇ
κ
o
(x) is accepted if
ˇ
κ
o
(x) < m(x).
Consider a single frame of data and note that the
estimates of
d
SNR(x) and
d
SOR(x) can be computed
pixel-by-pixel as
d
SNR(x) =
√
2
ˇ
A
√
ˇ
I
;
d
SOR(x) =
ˇ
A
ˇ
I
o
, (54)
where
ˇ
I
o
is the measured background offset. In addi-
tion, it is necessary to compute the estimate of
ˆ
κ
o
(x)
at pixel x. Based on the assumption of a flat surface
the true value of κ
o
(x) will only deviate from a con-
stant due to viewing angle of the surface θ
p
. This an-
gle is approximately constant for small field of view
cameras. Therefore, we approximate κ
o
(x) ≈ κ
o
over
pixels of the planar surface. Moreover, we find in
practice that the SNR and SOR over a single planar
surface are comparable and we can make an estimate
ˆ
κ
o
of κ
o
based on average statistics of this data set.
0 20 40 60 80 100
0
0.05
0.1
0.15
0.2
0.25
˘κ
o
Relative contribution of ˘κ
o
Figure 5: Normalized histogram of
ˇ
κ
o
(x) of a surface. Pix-
els with
ˇ
κ
o
(x) → ∞ (due to amplitude and phase) have been
scaled down to finite values.
A typical normalized histogram of
ˇ
κ
o
(x) for a sin-
gle frame of a planar surface is shown in Figure 5.
The heavy tail is associated with noisy data. We pro-
pose a pragmatic approach (a practical estimator) for
κ
o
using the harmonic mean
ˆ
κ
o
=
n
∑
n
i
1/
ˇ
κ
o(x)
i
(55)
It is reasonable to use the harmonic mean (Bodek,
1974) due to the fact that each individual
ˇ
κ
o
(x) is a
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
150

ratio distribution with different SNRs of the received
signal measured in TOF camera and the error mea-
surements of
ˇ
κ
o
(x) in denominator being greater than
that of a numerator.
The statistical test (52) can be applied to all pix-
els drawn from a planar surface. The parameters
d
SNR,
d
SOR,
ˆ
κ
o
estimated from the same data that is
then used in the test, however, the slight dependence
introduced is not believed to effect the overall valid-
ity of the test significantly if there are enough pixels
in the given observed surface (typically a 5×5) patch.
8 EXPERIMENTS AND RESULTS
We perform experiments in an indoor environment
where a TOF camera is placed conveniently at a dis-
tance of 3 meters from a flat white board while the
wall is about 6 meters from the camera as illustrated
in Figure 6. In addition there are various other objects
and lab equipment within the field of view of camera.
These objects offer different reflectivity and provide
a wide variety of characteristics for the experiments
undertaken. Our PMD 3k-S(PMD, 2002) TOF cam-
era provides 48×64 pixel resolution with a field of
view of 33.4
◦
×43.6
◦
.
Figure 6: Picture taken from a normal 2D camera for a tri-
pod mounted TOF camera setup.
The algorithm is applied to an entire frame and
a
ˇ
κ
o
(x) distribution is plotted for a planar surface (a
wall) (see Figure 5). The final range data as a function
of
ˇ
κ
o
(x) is obtained after applying the range image
filtering criterion (52) to the entire frame including
planar surface as shown in Figure 8.
The final6data after filtering is consistent with a
reliable measurement of range values. It is quite clear
that
ˇ
κ
o
(x) value is almost consistent for the entire
range (0-7.5 meters) of the camera with noisy data
pixels (see Figure 7) showing a variation in
ˇ
κ
o
(x) val-
ues as shown in Figure 8. The algorithm is neither
effected by the distance of the object from the cam-
era (within camera range) nor the reflectively/surface
X: 9 Y: 5
Range: 1.014
X: 56 Y: 9
Range: 0.077
X: 9 Y: 26
Range: 1.951
10 20 30 40 50 60
5
10
15
20
25
30
35
40
45
1 2 3 4 5 6 7
meters
Figure 7: Range image plot of a PMD TOF camera with
three marked noisy (in-correct) range pixels.
10 20 30 40 50 60
5
10
15
20
25
30
35
40
45
Figure 8: Filtered
ˇ
κ
o
(x) plot with regions of consistent
ˇ
κ
o
and noisy pixels shown in red color. Three pixels marked
with arrows relate to marked noisy range pixels in Figure 7.
texture for wide range of integration times and SNR
conditions compared to other image algorithms that
are otherwise susceptible to surface conditions. It has
been observed that in real environments the planar
model works extremely well even for non-planar sur-
faces and is robust enough for reliable range measure-
ments. Since the applied algorithm can filter the entire
frame, the algorithm is quite efficient and effective for
TOF based applications.
9 CONCLUSIONS
The use of Time-of-flight (TOF) cameras is increasing
in various applicati6ns ranging from medical to auto-
motive. TOF manufacturer companies are progress-
ing rapidly to increase the resolution and range of the
camera. However, the range pixel reliability has not
been addressed effectively in the literature. The use of
radiometric model for all the available measurement
parameters helps in formulating a robust range relia-
bility criterion that is independent of scene reflectivity
and will make a substantial difference to how range
pixel reliability is classified.
RADIOMETRIC RANGE IMAGE FILTERING FOR TIME-OF-FLIGHT CAMERAS
151

ACKNOWLEDGEMENTS
This work is supported by Seeing Machines Ltd. and
the Commonwealth of Australia, through the Coop-
erative Research Centre for Advanced Automotive
Technology.
REFERENCES
Alldrin, N., Zickler, T., and Kriegman, D. (2008). Pho-
tometric stereo with non-parametric and spatially-
varying reflectance. In Proc. IEEE Conference
on Computer Vision and Pattern Recognition CVPR
2008, pages 1–8.
Bodek, A. (1974). The mean of several quotients of two
measured variables. SLAC Technical Note.
Bonny, J.-M., Renou, J.-P., and Zanca, M. (1996). Opti-
mal measurement of magnitude and phase from MR
data. Journal of Magnetic of Resonance, Series B,
113(2):136–144.
B
¨
uttgen, B., Lustenberger, F., and Seitz, P. (2006). Demod-
ulation pixel based on static drift fields. IEEE Trans.
Electron Devices, 53(11):2741–2747.
Cook, R. L. and Torrance, K. E. (1982). A reflectance
model for computer graphics. ACM. Trans. on Graph-
ics, 1(1):7–24.
Fardi, B., Dousa, J., Wanielik, G., Elias, B., and Barke, A.
(2006). Obstacle detection and pedestrian recognition
using a 3D PMD camera. In Proc. IEEE Intell. Vehi-
cles Symp., pages 225–230.
Foley, J. D., Da, A. v., Feiner, S. K., and Hughes, J. F.
(1997). Computer Graphics: Principles and Prac-
tices. Addisin-Wesley Publishing Company, Inc.
Forsyth, D. A. and Ponce, J. (2003). Computer Vision: A
Modern Approach. Prentice Hall.
Horn, B. (1986). Robot Vision. The MIT Press.
Horn, B. K. P. (1977). Image intensity understanding. Arti-
ficial Intelligence, 8(2):201–231.
Kahlmann, T., Remondino, F., and Guillaume, S. (2007).
Range imaging technology: new developments and
applications for people identification and tracking. In
Proc. SPIE-IS&T Electronic Imaging, volume 6491,
San Jose, CA, USA.
Kahlmann, T., Remondino, F., and Ingensand, H. (2006).
Calibration for increased accuracy of the range imag-
ing camera SwissRanger. In Proc. International
Archives of Photgrammetry, Remote Sensing and Spa-
tial Information Sciences, ISPRS Commission V Sym-
posium, volume XXXVI, pages 136–141.
Klasing, K., Althoff, D.,Wollherr, D., and Buss, M. 2009
Comparison of surface normal estimation methods for
range sensing applications. In Proc. IEEE Interna-
tional Conference on Robotics and Automation ICRA
09, pages 32063211.
Kuhnert, K.-D. and Stommel, M. (2006). Fusion of stereo-
camera and PMD-camera data for real-time suited
precise 3D environment reconstruction. In Proc.
IEEE/RSJ Int. Conf. Intell. Robot. Systs.
Lange, R. and Seitz, P. (2001). Solid-state time-of-flight
range camera. IEEE J. Quantum Electron., 37:390–
397.
Lindner, M. and Kolb, A. (2006). Lateral and depth calibra-
tion of PMD-distance sensors. In Proc. International
Symposium on Visual Computing (ISVC06), volume 2,
pages 524–533. Springer.
Lindner, M. and Kolb, A. (2007). Calibration of the
intensity-related distance error of the PMD TOF-
camera. In Proc. SPIE, Intelligent Robots and Com-
puter Vision XXV: Algorithms, Techniques, and Active
Vision, volume 6764.
Luan, X. (2001). Experimental Investigation of Photonic
Mixer Device and Development of TOF 3D Ranging
Systems Based on PMD Technology. PhD thesis, De-
partment of Electrical Engineering and Computer Sci-
ence at University Of Siegen.
Ma, Y., Soatto, S., Ko
ˇ
seck
´
a, J., and Sastry, S. S. (2003).
An Inviation to 3-D Vision: From Images to Geomtric
Models. Springer Verlag. Ch. 2.
Meier, E. and Ade, F. (1997). Tracking cars in range image
sequnces. In Proc. IEEE Int. Conf. Intell. Trans. Systs.,
pages 105–110.
Moller, T., Kraft, H., Frey, J., Albrecht, M., and Lange,
R. (2005). Robust 3D measurement with PMD sen-
sors. In Proc. 1st Range Imaging Research Day, ETH
Zurich, Zurich, Switzerland.
Mufti, F. and Mahony, R. (2009). Statistical analysis of
measurement processes for time-of-flight cameras. In
Proc. SPIE Videometrics, Range Imaging, and Appli-
cations X, volume 7447-21.
PMD (2002). PMD tech. http://www.pmdtec.com.
Pulli, K. and Pietikainen, M. (1993). Range image segmen-
tation based on decomposition of surface normals. In
Proc. 8th Scandinavian Conference on Image Analy-
sis, pages 893–899.
Radmer, J., Fuste, P. M., Schmidt, H., and Kruger, J. (2008).
Incident light related distance error study and cali-
bration of the PMD-range imaging camera. In IEEE
Conf.Computer Vision and Pattern Recognition Work-
shops, 2008, pages 16.
Sillion, F. X. and Puech, C. (1994). Radiosity and Global
Illumination. Morgan Kaufmann.
Ye, C. and Hegde, G.-P. M. (2009). Robust edge extrac-
tion for SwissRanger SR-3000 range images. In Proc.
IEEE International Conference on Robotics and Au-
tomation ICRA09, pages 24372442.
Zhang, R., Tsai, P.-S., Cryer, J., and Shah, M. (1999). Shape
from shading: A survey. IEEE Trans. Pattern Anal.
Mach. Intell., 25(11):1416–1421.
Zheng, Q. and Chellappa, R. (1991). Estimation of illu-
mination direction, albedo, and shape from shading.
IEEE Trans. Pattern Anal. Mach. Intell., 13(7):680–
702.
Zhou, S., Aggarwal, G., Chellappa, R., and Jacobs, D.
(2007). Appearance characterization of linear lam-
bertian objects, generalized photometric stereo, and
illumination-invariant face recognition. IEEE Trans.
Pattern Anal. Mach. Intell., 29(2):230–245.
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
152
