SPEEDED UP IMAGE MATCHING USING SPLIT AND

EXTENDED SIFT FEATURES

Faraj Alhwarin, Danijela Ristić–Durrant and Axel Gräser

Institute of Automation, University of Bremen, Otto-Hahn-Alle NW1, D-28359 Bremen, Germany

Keywords: Speeded Up Features Matching, Split SIFT, Extended SIFT.

Abstract: Matching feature points between images is one of the most fundamental issues in computer vision tasks. As

the number of feature points increases, the feature matching rapidly becomes a bottleneck. In this paper, a

novel method is presented to accelerate features matching by two modifications of the popular SIFT

algorithm. The first modification is based on splitting the SIFT features into two types, Maxima- and

Minima-SIFT features, and making comparisons only between the features of the same type, which reduces

the matching time to 50% with respect to the original SIFT. In the second modification, the SIFT feature is

extended by a new attribute which is an angle between two independent orientations. Based on this angle,

SIFT features are divided into subsets and only the features with the difference of their angles less than a

pre-set threshold value are compared. The performance of the proposed methods was tested on two groups

of images, real-world stereo images and standard dataset images. The presented experimental results show

that the feature matching step can be accelerated 18 times with respect to exhaustive search without losing a

noticeable portion of correct matches.

1 INTRODUCTION

Matching a given image with one or many others is

a key task in many computer vision applications

such as object recognition, images stitching and 3D

stereo reconstruction. These applications require

often real-time performance. The matching is

usually done by detecting and describing key-points

in the images then applying a matching algorithm to

search for correspondences.

Classic key-point detectors such as Difference of

Gaussians (DoG) (Lowe, 2004), Difference of

Means (DoM) (Bay et al., 2008) and Harris corner

detector (Harris

& Stephens, 1988) use simple

attributes like blob-like shapes or corners.

For the key-point description a variety of key-

point descriptors have been proposed such as the

Scale Invariant Feature Transform (SIFT) (Lowe,

2004), Speeded Up Robust Features (SURF) (Bay et

al., 2008) and Gradient Location and Orientation

Histogram (GLOH) (Mikolajczyk & Schmid, 2005).

To robustly match the images, point-to-point

correspondences are determined using similarity

measure for Nearest Neighbour (NN) search such as

Euclidean distance. After that, the RANdom Sample

Consensus (RANSAC) method is applied to estimate

the correct correspondences (inliers).

The combination of the DoG detector and SIFT

descriptor proposed in (Lowe, 2004) is currently the

most widely used in computer vision applications

due to the fact that SIFT features are highly

distinctive, and invariant to scale, rotation and

illumination changes. In addition, SIFT features are

relatively easy to extract and to match against a large

database of local features. However, the main

drawback of SIFT is that the computational

complexity of the algorithm increases rapidly with

the number of key-points, especially at the matching

step due to the high dimensionality of the SIFT

feature descriptor.

In order to overcome the main SIFT drawback,

various modifications of the SIFT algorithm have

been proposed. In general, the strategies dealing

with the acceleration of SIFT features matching can

be classified into three different categories: reducing

the descriptor dimensionality, parallelization and

exploiting the power of hardware (GPUs, FGPAs or

multi-core systems) and Approximate Nearest

Neighbor (ANN) searching methods.

(Ke

& Sukthankar, 2004) applied Principal

Components Analysis (PCA) to the SIFT descriptor.

The PCA-SIFT reduces the SIFT feature descriptor

287

Alhwarin F., Risti

c –Durrant D. and Gräser A. (2010).

SPEEDED UP IMAGE MATCHING USING SPLIT AND EXTENDED SIFT FEATURES.

In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 287-295

DOI: 10.5220/0002820102870295

 SciTePress

dimensionality from 128 to 36, so that the PCA-

SIFT is fast for matching, but seems to be less

distinctive than the original SIFT as demonstrated in

a comparative study by (Mikolajczyk & Schmid,

2005).

(Bay et al., 2008) developed the Speeded Up

Robust Feature (SURF) method that is a

modification of the SIFT method aiming at better

run time performance of features detection and

matching. This is achieved by two major

modifications. In the first one, the Difference of

Gaussian (DoG) filter is replaced by the Difference

of Means (DoM) filter. The use of the DoM filter

speeds up the computation of features detection due

to the exploiting integral images for a DoM

implementation. The second modification is the

reduction of the image feature vector length to half

the size of the SIFT feature descriptor length, which

enables quicker features matching. These

modifications result in an increase computation

speed by a factor 3 compared to the original SIFT

method. However, this is insufficient for real-time

requirements.

In recent years, several papers (Heymann et al.,

2007) were published addressing the use of the

parallelism of modern graphics hardware (GPU) to

accelerate some parts of the SIFT algorithm, focused

on features detection and description steps. In

(Charriot

& Keriven, 2008) GPU power was

exploited to accelerate features matching. These

GPU-SIFT approaches provide 10 to 20 times faster

processing allowing real-time application.

The matching step can be speeded up by

searching for the Approximate Nearest Neighbor

(ANN) instead of the exact nearest neighbor. The

most widely used algorithm for ANN is the kd-tree

(Firedman et al., 1977), which successfully works in

low dimensional search space, but performs poorly

when feature dimensionality increases. (Lowe, 2004)

used the Best-Bin-First (BBF) method, which is

expanded from kd-tree by modification of the search

ordering so that bins in feature space are searched in

the order of their closest distance from the query

feature and stopping search after checking the first

200 nearest-neighbor candidates. The BBF provides

a speedup factor of 2 times faster than exhaustive

search while losing about 5% of correct matches. In

(Muja & Lowe., 2009) Muja and Lowe compared

many different algorithms for approximate nearest

neighbor search on datasets with a wide range of

dimensionality and they found that two algorithms

obtained the best performance, depending on the

dataset and the desired precision. These algorithms

used either the hierarchical k-means tree or multiple

randomized kd-trees.

In this paper, a novel strategy which is distinctly

different from all three of the above mentioned

strategies, is introduced to accelerate the SIFT

features matching step. The paper contribution is

summarized in two points.

Firstly, in the key-point detection stage, the SIFT

features are split into two types, Maxima and

Minima, without extra computational cost and at the

matching stage only features of the same type are

compared. since correct match can not be expected

between two features of different types.

Secondly, in the orientation assignment stage the

SIFT feature is extended by a new attribute without

extra computational cost. The novel attribute is an

angle between the original SIFT feature orientation

and a new different orientation

. Hence SIFT

features are divided into a few clusters based on the

introduced angle. At the matching stage, only

features of the almost same angle are compared. The

idea behined this is that correct matches can be

expected only between two features whose angles

differ for less than a pre-defined threshold.

The proposed method can be generalized for all

local feature-based matching algorithms which

detect two or more types of key-points (e.g. DoG,

LoG, DoM) and whose descriptors are rotation

invariant, where two different orientations can be

assigned (e.g. SIFT, SURF, GLOH).

2 ORIGINAL SIFT METHOD

The Scale Invariant Feature Transform (SIFT)

method, proposed by Lowe (Lowe, 2004), takes an

image and transforms it into a set of local features.

The SIFT features are extracted through the

following three stages:

1. Feature Detection and Localization: In this

stage, the locations of potential interest points in the

image are determined by detecting the extrema of

Difference of Gaussian (DoG) scale space. For

searching scale space extrema, each pixel in the

DoG images is compared with its 26 neighbors in

3×3 regions of scale-space. If the pixel is

lower/larger than all its neighbors, then it is labelled

as a candidate key-point. Each of these key-points is

exactly localized by fitting a 3D quadratic function

computed using a second order Taylor expansion

around key-point location. Hence key-points are

filtered by discarding points of low contrast and

points that correspond to edges.

2. Feature Orientation Assignment: An orientation

is assigned to each key-point based on local image

gradient data. For each pixel in a certain region

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

288

around the key-point location, the first order

gradients are calculated according to the following

equations:

(1,,)(1,,)

(, 1, ) (, 1, )

gLx y Lx y

gLxy Lxy

=+ −−

=+−−

(1)

where

(, , )Lxy

is the grey value of the pixel

(, )pxy in the image blurred by a Gaussian Kernel

whose size is determined by

The gradient magnitude and orientation for each

pixel are computed respectively as follows:

() )

)

(, ) (

(,)arctan(

mx y g g

xy g g

(2)

From gradient data (magnitudes and orientations)

of pixels within the region

R , a 36-bin orientation

histogram is constructed covering the range of

orientations [-180°, 180°] (each bin covers 10°). For

each bin, the histogram is calculated according to

following formulas:

( ) int( ( , ) / 10) 17ori i x y

=−

(3)

where

(, ) [0,360)xy

∈° °

() ( , ) ( , )

mag i m x y m x y=

∑∑

(4)

where

( ,)

mxyare gradient magnitudes of pixels

that have discrete gradient orientations equal to

()ori i . An example of the orientation histogram is

given in Figure1.

Figure 1: 36 bins orientation histogram constructed using

local gradient data around a key-point.

The orientation of the SIFT feature is defined as

the orientation corresponding to the maximum bin of

the orientation histogram according to:

()

max

arg max ()ori mag i

(5)

3. Feature Description: A local feature descriptor is

computed at each key-point based on the local image

gradient data. The region around the key-point is

divided into 16 square boxes. For each box an eight

bin orientation histogram is calculated from gradient

data of pixels within the corresponding box relative

to the feature orientation to provide rotation

invariance. Finally, all 16 resulted eight bin

orientation histograms is transformed into 128-D

vector. The vector is normalized to unit length to

achieve the invariance against illumination changes.

Therefore the original SIFT feature consists of

four attributes, a location

(, )Pxy, a scale

(level

of scale space where is the key-point), an orientation

max

and a 128-D descriptor vector

V . Hence, the

original SIFT feature can be written as:

max

(,, , )

σθ

3 EXTENDED SIFT FEATURES

Generally, if a scene is captured by two cameras or

by one camera but from two different viewpoints,

the corresponding points in two resulted images,

which represent images of the same 3D point, will

have different image coordinates, different scales,

and different orientations, though, they must have

almost similar descriptors which are used to match

the images using a similarity measures.

In order to speed-up the features matching, it is

assumed in this paper that two independent

orientations can be assigned to each feature so that

the angle

between them stays almost unchanged

for all correct corresponding points even in the case

of the images captured under different conditions

such as viewing geometry and illumination changes.

The idea of using an angle between two

independent orientations is aimed at avoidance of

comparison of a great portion of features that can not

be matched in any way. This leads to a significant

acceleration of the matching step. Hence, the reason

for proposing SIFT feature angle

is twofold.

On the one hand, to filter the correct matches, so

that a correct match

can be established

between two features

and

, which belong

respectively to images 1 and 2, if and only if the

difference between their angles

and

is less

than a preset threshold value

()mag i

()ori i

180−° 180

ma x

SPEEDED UP IMAGE MATCHING USING SPLIT AND EXTENDED SIFT FEATURES

289

φφφ

Δ= − ≤

(6)

On the other hand, the reason for proposing SIFT

feature angle

is to accelerate the SIFT feature

matching because there is no necessity to compare

two features if the difference between their angles is

larger than a preset threshold

3.1 Matching Speeded-Up Factor

Assuming two images to be matched whose feature

angles

{

}

and

{

}

are considered as random

variables

Φ and

Φ respectively.

In the case of correct matches the random

variables

Φ and

Φ are dependent on each other

since the angle differences of correct matches are

equal to zero which correspond to the ideal image

matching case.

In contrast, the random variables

Φ and

are

independent of each other for incorrect matches

while the angle differences of incorrect matches are

somehow distributed in the range

[,]

−

Therefore, the difference

ΔΦ = Φ − Φ for the

incorrect matches has a probability density function

(PDF) distributed over the whole angle range

[,]

−

, whereas the PDF of ΔΦ for the correct

matches is concentrated in the so-called range of

correct matches, which is the narrow range about 0°.

Generally, if the random variables

and

Φ are independent and uniformly distributed in the

range

[,]

− , their difference ΔΦ is uniformly

distributed in the same range (Simon et al., 1995).

If a matching procedure, which compares only

the features having angle differences

ΔΦ in the

range of correct matches, is used in the case of

uniform distribution of

ΔΦ

for incorrect matches,

then the matching process is accelerated by a speed-

up factor

SF . Speed-up factor can be expressed as

the ratio between the width of the whole angle range

360

total

w =° and the width of the range of correct

matches

cor

w :

360

total

cor cor

(7)

3.2 SIFT Feature Angle

It is suggested that a SIFT feature is extended with

an angle that meets the following conditions:

The angle has to be invariant to the geometric

and photometric transformations (the invariance

condition);

The angle has to be uniformly distributed in the

range

[,]

−

(the “equally likely” condition).

To assign an angle to the SIFT feature, two

orientations are required.

The invariance condition is guaranteed only if

these orientations are different, whereas the “equally

likely” condition is guaranteed if the orientations are

independent and uniformly distributed in the range

[,]

−

As mentioned in Section 2, the original SIFT

feature has already an orientation

max

. Therefore, it

is only necessary to define one new orientation.

Firstly, the angle

corresponding to the

vector sum of all orientation histogram bins is

considered and the difference between the suggested

orientation and the original SIFT feature orientation

maxsum sum

θθ

=−is assigned to the SIFT feature as

the SIFT feature angle

φφ

= .

Figure 2: The vector sum of the bins of an eight

orientation histogram.

Figure 2 presents geometrically the vector sum

of an eight bins orientation histogram (eight bins

only for the sake of simplicity), whereas the used

orientation histogram has 36 bins as explained in

Section 2 for the case of the original SIFT. Hence,

mathematically, the proposed orientation

calculated according to:

max

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

290

()

()sin ()

arctan

()cos ()

sum

mag i ori i

=−

⎛⎞

⎜⎟

⎝⎠

⋅

∑

⋅

∑

(8)

Since

is different from

max

meets

the invariance condition.

To examine whether

meets the “equally

likely” condition, it is considered as a random

variable

Φ .

The PDF of

Φ is estimated using 725356

SIFT features extracted from 600 test images (400

benchmark images (Image-Dataset) and 200 stereo

images from a real-world robotic application) Some

examples of used images are given in Section 5.

The PDF of

Φ was computed by dividing the

angle space [-180°,180°] into 36 sub-ranges, where

each sub-range cover 10°, and by counting the

numbers of features whose angle

belong to

each sub-range.

As evident from Figure 3 about 60% of features

have angles

falling in the range [-30°,30°]. The

reason of this outcome is the high dependency

between

max

and

due to the fact that the

corresponds to the vector sum of all orientation

histogram bins including the bin which corresponds

max



-180 -150 - 120 -90 -60 -30 0 30 60 90 120 150 18

Angle(degree)

Φsum Φtran,0 Φtran,1

Φtran,2 Φtran,3 Φtran,4

Figure 3: The experimental PDFs of

Φ and

,tran

for SIFT features extracted from 600 test images.

The

max

is the dominant orientation in the patch

around the key-point so that it has dominant

influence to the

. Due to the high dependency

between

max

and

does not meet the

“equally likely” condition and can not be considered

as SIFT feature angle.

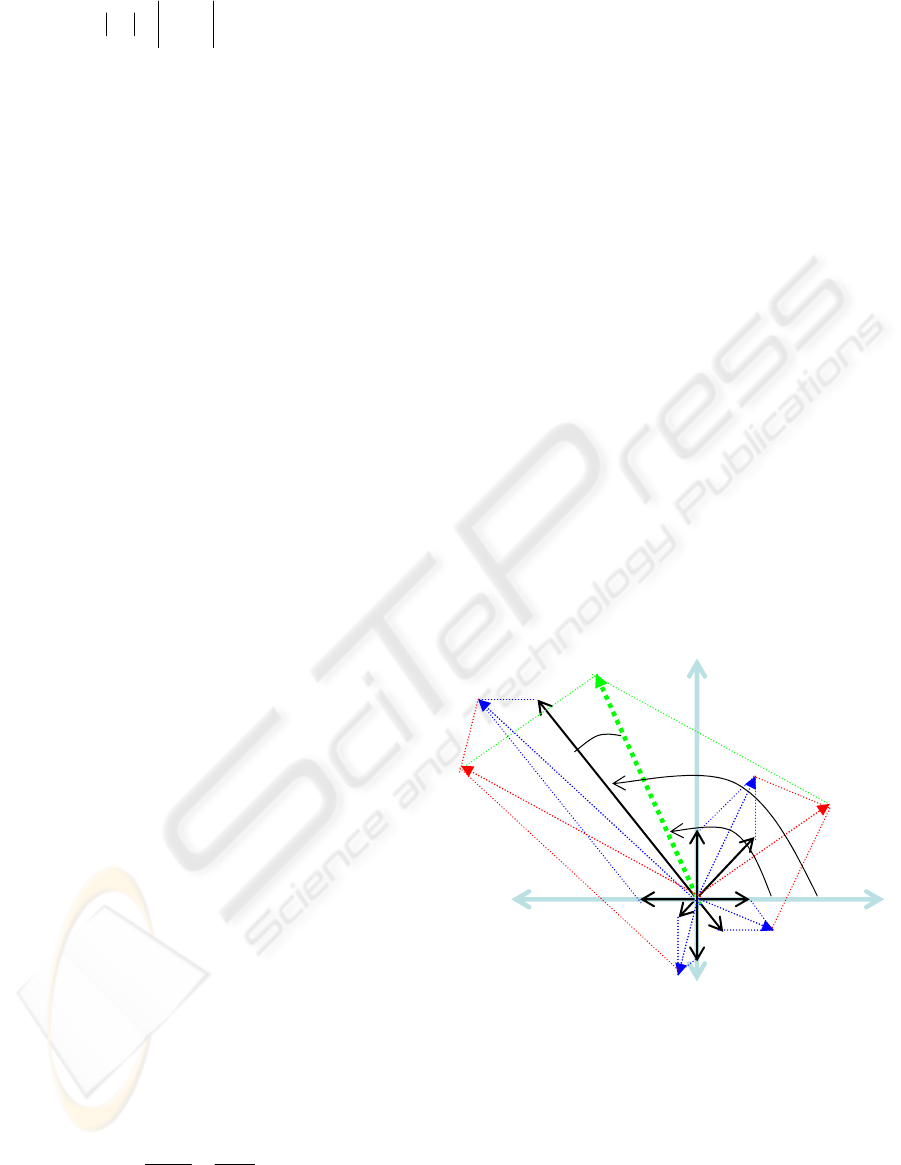
To define an appropriate SIFT feature angle,

orientations

,tran

are further suggested These

orientations are computed as the vector sums of all

orientation histogram bins excluding the maximum

bin and

of its neighbour bins at the left and at the

right side as follows:

()

[m 1,m 1]

()sin ()

()cos ()

()sin ()

()cos ()

arctan

tran

mag i ori i

=−

≠

=−

≠

=−

∉− +

=−

∉− +

⎛⎞

⋅

∑

⎜⎟

⋅

∑

⎜⎟

⎝⎠

⎛⎞

⋅

∑

⎜⎟

⋅

∑

⎜⎟

⎝⎠

()

[m ,m ]

()sin ()

()cos ()

mag i ori i

κκ

=−

∉− +

=−

∉− +

⎛⎞

⋅

∑

⎜⎟

⋅

∑

⎜⎟

⎝⎠

(9)

where arg max( ( ))mmagi

The PDFs of the random variables

,tran

corresponding to angles

,,maxtran tran

κκ

φθθ

=− are

estimated in the same manner as the PDF of

Φ ,

performing the experiments over 725356 SIFT

features extracted from the same 600 test images

mentioned before. The measured PDFs of

,tran

(for

0,1, 2, 3, 4

) are shown in Figure 3. It is

evident from Figure 3 that the

,1tran

Φ has a PDF

which is the closest to the uniform distribution.

Therefore, the angle

,1tran

meets both conditions,

invariance and “equally likely” condition, and it can

be considered as a new attribute

of the SIFT

feature,

,1tran

φφ

= . With this extension a SIFT

feature becomes

max

(,, , ,)FP V

SPEEDED UP IMAGE MATCHING USING SPLIT AND EXTENDED SIFT FEATURES

291

4 SPLIT AND EXTENDED SIFT

FEATURES MATCHING

Assuming that two sets of extended SIFT features

are given:

;{ 1, 2,..., }

RFi r==

;{ 1, 2,...., }

LFj l== ,

containing respectively

r and l features. The

number of possible matches

()

FF is equal to

rl⋅ . Among these possible matches a small number

of correct matches may exist. Considering of all

possible matches is computationally expensive.

In the following two novel matching procedures

are proposed to accelerate the matching process. The

main idea behind both procedures is comparison of

only features that share the same property which

may lead to correct matches.

4.1 Split SIFT Features Matching

As said in Section 2, the SIFT feature locations are

detected as the extrema of the scale space. Extrema

can be Minima or Maxima so that there are two

types of SIFT features, Maxima and Minima SIFT

features.

Through the extraction of SIFT features from

600 different images in considered experiments, it

was found that the number of Maxima is almost

equal to the number of Minima SIFT features

extracted from the same image. The matching time

was reduced by 50% with respect to the original

SIFT matching starting from the idea that no correct

match can be expected between two features of

different types. The claim that no correct matches

between Minima and Maxima SIFT features is

experimentally supported. Namely, it was found that

the features of each correct match are always from

the same type.

To declare the matching time reduction by

splitting the SIFT features, it is assumed that the

number of features extracted from the first and the

second image are expressed as:

max min

rr r=+

max min

ll l=+

(10)

where

max max

)(rl and

min min

()rl are the numbers of

Maxima and Minima SIFT features respectively.

The matching time without regard to the type of

features, that is the time of exhaustive search, is:

exh

Trl

⋅

(11)

The matching time, in the case of comparison of

only features of the same type, is proportional to the

following sum:

max max min minsplit

Trlrl=⋅+⋅

(12)

Substituting the assumption

max min

2rrr≅≅

and

max min

2lll≅≅ into (12) one obtains:

split

exh

TrlT=⋅ =

(13)

Hence, the matching time is decreased by 50% in

respect to exhaustive search.

4.2 Extended SIFT Features Matching

A set of SIFT feature angle differences

{ ; 1, 2,..., }

ij i j

ij r l

φφφ

=− = ⋅

is established for

the SIFT feature angles

{ ; 1, 2, ..., }

and

{ ; 1, 2,..., }

of the extended SIFT features

from the given sets R and L.

Considering the angle differences

Δ as a

random variable

Φ , the PDFs of

ΔΦ for both

correct and incorrect matches are measured in

experiments over considered 600 images.

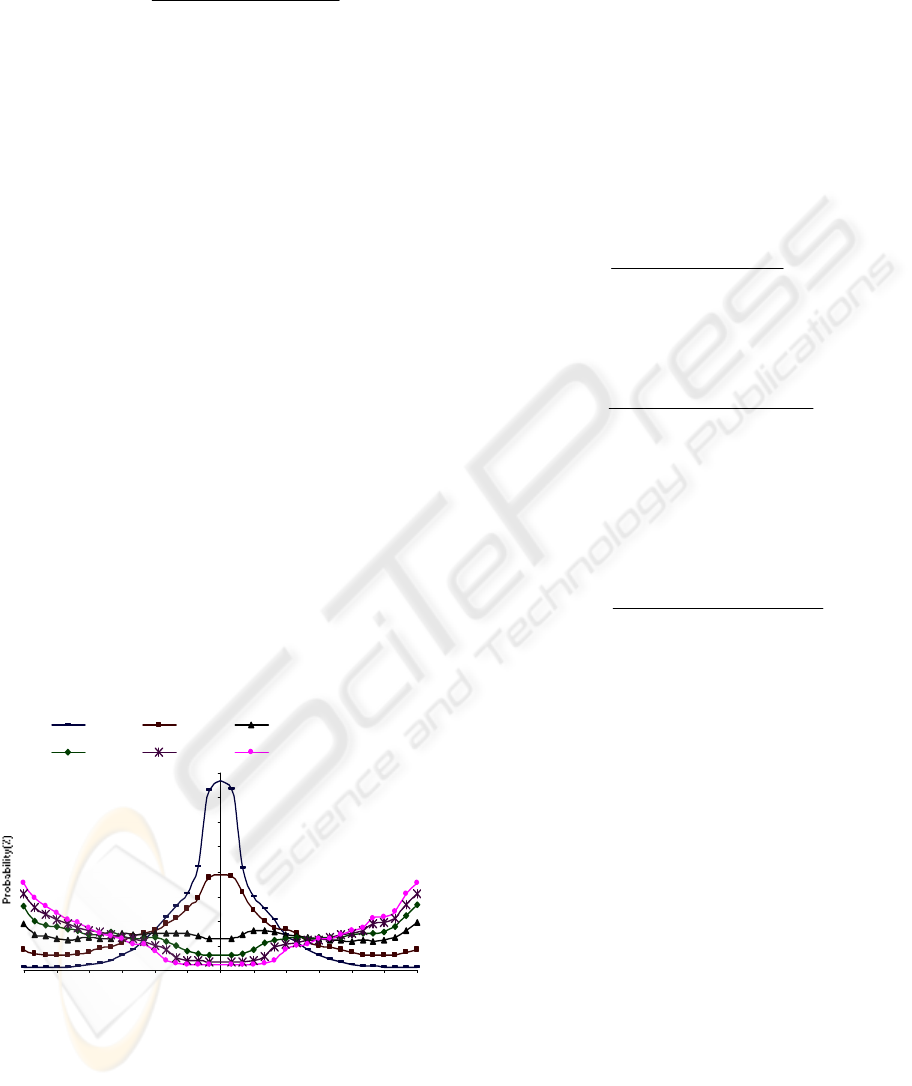
The measured PDFs are shown in Figure 4. It can

be seen from Figure 4 that about 92 % of correct and

only 12% of possible matches belong to [-20°,20°].

Therefore, in order to find correct matches it is

needed to treat only 12% of possible matches which

can speed-up the features matching significantly.

To exploit this outcome, SIFT features are

divided into several subsets based on their angles.

The SIFT features of each subset are compared only

with the features of some subsets, so that the

resulting correspondences must have absolute

differences of angles less than a pre-set threshold.

Here a threshold of 20 is selected because almost all

correct matches have angle differences in the range

[-20°, 20°] as illustrated in Figure 4.

Consider that each of the sets of features

R and

L are divided into

subsets, so that the first subset

contains only the SIFT features whose angles belong

[, 2 )b

ππ π

−−+ and the

i subset contains

features whose angles belong to

[2(1), 2)ib ib

ππππ

−+ − −+ . Consequently, the

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

292

b subset contains features whose angles belong to

[2(1),)bb

ππ

−+ − .

-180 -140 -100 -60 -20 20 60 100 140 180

Angle (Degree)

Probability (%)

PDF o f ∆Φ for

possible matches

PDF o f ∆Φ for

co rr ect mat ches

Figure 4: The experimental PDF of the angle difference

for the incorrect and the possible matches.

The number of features of the both sets can be

expressed as:

01 1

...

rr r r

−

=+++

01 1

...

ll l l

−

=+++

(14)

Because of the evenly distribution of feature

angles over the range of their angles

[,]

− as

shown in Figure 3, the features are almost equally

divided into several subsets. Therefore, it can be

asserted that the feature numbers of each subset are

almost equal to each other.

01 1

....

rr r rb

−

≅≅≅

01 1

....

ll l lb

−

≅≅≅

(15)

To exclude matching of features that have a

difference of angles outside the range

[,]aa

−

°°,

each subset is matched to its corresponding one and

n neighbouring subsets to the left and to the right

side as illustrated in Figure 5. In this case the mat-

ching time is proportional to the following term:

() ()

(2 1)

jin

bin

ijin

extend

Trl

rl n

−

=−

−+

==−

⎛⎞

⎜⎟

⎝⎠

=⋅

∑

⋅

≅

∑∑

⋅⋅ +

≅

(16)

Therefore, the achieved speed-up factor to

exhaustive search is equal to:

extend

(17)

The relation between

n , a and b is as follows:

()

360

21 2. 12

360

nan

⎢⎥

⎛⎞

⎢⎥

⎜⎟

⎢⎥

⎜⎟

⎝⎠

⎢⎥

⎝⎠

⎣⎦

⋅⋅

⋅+ ⋅ = ⇒ = −

(18)

where

⎢

⎥

⎣

⎦

•

represents the first integer value larger

than or equal to

•

Substituting (18) into (17) yields:

360

extend

(19)

The result (19) means that if it is aimed to

exclude matching of features that have angle

differences outside the range [-20°,20°], then the

matching step is accelerated by a factor 9.

When this modification of original SIFT feature

matching is combined with the split SIFT features

matching, the obtained speedup factor is 18 without

loosing a noticeable portion of correct matches. This

is illustrated with the experimental results presented

in the next section.

Figure 5: The matching procedure through the comparison

of features having angle differences smaller than a pre-set

threshold.

5 EXPERIMENTAL RESULTS

The proposed method for speeding up feature

matching based on split and extended SIFT features

was tested using both a standard image dataset, and

real world stereo images.

The used image dataset *ID consists of about

500 images of 34 different scenes. Each scene is

represented with a number of images taken under

different photometric and geometric conditions.

Some examples of the images used in the

experiments, whose results are presented here, are

given in Figure 6.

Stereo images were grabbed by the stereo camera

)

2,4bb

ππ

⎡

⎢

⎣

)

0,2 b

⎡

⎢

⎣

)

2,0b

⎡

⎢

⎣

−

)

2( 1) , 2nbnb

ππ

⎡

⎢

⎣

−− −

)

2,2(1)nb n b

ππ

⎡

⎢

⎣

−−+

)

2( 1) , 2( 2)nbn b

ππ

⎡

⎢

⎣

−+ −+

)

2( 1) ,2( 2)nbnb

⎡

⎢

⎣

)

2,2(1)nb n b

ππ

⎡

⎢

⎣

)

2( 1) ,2nbnb

ππ

⎡

⎢

⎣

−

)

2,4bb

ππ

⎡

⎢

⎣

)

0,2 b

⎡

⎢

⎣

)

2,0b

⎡

⎢

⎣

−°

SPEEDED UP IMAGE MATCHING USING SPLIT AND EXTENDED SIFT FEATURES

293

(a) (b)



Figure 6: Some of the standard dataset images of scenes

captured under different conditions: (a) viewpoint, (b)

light changes, (c) zoom, (d) rotation.

system of the rehabilitation robotic system FRIEND

(Functional Robot arm with frIENdly interface for

Disabled people) (Martens et al., 2007). FRIEND is

intended to support the user in daily life activities

which demand object manipulation such as serving a

drink and preparing and serving a meal. The crucial

for autonomous object manipulation is precise 3D

object localization. The key factor for reliable 3D

reconstruction of object points is correct matching of

correspondence points in stereo images. Hence,

stereo robot vision is a typical application where fast

and reliable feature matching is of utmost interest.

Some examples of stereo images showing

FRIEND environment in “serving a drink” robot

working scenario are given in Figure 7.

In order to evaluate the effectiveness of the

proposed method, its performance was compared

with the performances of two algorithms for ANN

(hierarchical k-means tree and randomized kd-trees).

Figure 7: Stereo images from a real-world robotic

application used in the experiments.

Comparisons were performed using the Fast

Library for Approximate Nearest Neighbors

**(FLANN), which is a library for performing fast

approximate nearest neighbour searching in high

dimensional spaces. For all experiments, the

matching process is carried out under different

precision degrees making trade off between

matching speedup and matching accuracy.

The precision degree is defined as the ratio

between the number of correct matches returned

using the considered algorithm and the number of

correct matches returned using exhaustive search,

*http://lear.inrialpes.fr/people/Mikolajczyk/Database/index.html

**http://people.cs.ubc.ca/~mariusm/index.php/FLANN/

whereas the speedup factor is defined as the ratio

between the exhaustive matching time and the

matching time for the corresponding method

For both ANN algorithms, hierarchical k-means

trees and randomized kd-trees, the precision is

adjusted by the number of nodes to be examined,

whereas for the proposed “Split and Extended SIFT”

method, the precision is determined by adjusting the

width of the range of correct matches

cor

(explained in Section 3). The correct matches are

determined using the Nearest Neighbor Distance

Ratio matching strategy (Lowe, 2004) with distance

ratio equal to 0.6, followed by RANSAC algorithm

to keep only inliers.

Two experiments were run to evaluate proposed

method, on real stereo images and on the images of

the dataset ID. In the first experiment, SIFT features

are extracted from 200 stereo images. Each two

corresponding images are matched using all three

considered algorithms under different degrees of

precision. The experimental results are shown in

Figure 8.

0,1

100

1000

50 60 70 80 90 100

Precision(%)

Speedup (SF)

Split&Extended SIFT K-Means Tree Rand, KD-Trees

Figure 8: Trade-off between matching speedup and

matching precision for real stereo image matching.

As can be seen from Figure 8, the performance

of the proposed method outperforms both ANN

algorithms for all precisions. For precision around

99% level, the proposed method provides a speedup

factor of about 20. For the lower precision degree

speedup factor is much higher.

As evident from Figure 8 by using proposed

“Split and extended SIFT” the speedup factor

relative to exhaustive search can be increased to 80

times while still returning 70% of the correct

matches.

The second experiment was carried out on the

images of the dataset ID. As said before, this dataset

consists of about 500 images of various contents.

These images represent images of 34 different

scenes taken under different conditions such as

rotation, zoom, light and viewpoint changes.

For the performed experiments the images of

dataset are grouped according to these different con-



VISAPP 2010 - International Conference on Computer Vision Theory and Applications

294

0,1

100

1000

50 60 70 80 90 100

0,1

100

50 60 70 80 90 100

0,1

100

1000

50 60 70 80 90 100

0,1

100

50 60 70 80 90 100

(a) (b)

(c)

(d)

Figure 9: Trade-off between matching speedup (SF) and

matching precision for image groups (a) light, (b)

viewpoint, (c) rotation, (d) zoom changes.

ditions into viewpoint, zoom, rotation and light

group. For each group, SIFT features are extracted

from each image and pairs of two corresponding

images are matched using hierarchical k-means tree,

randomized kd-trees and proposed “Split and

Extended SIFT”, with different degrees of precision.

The experimental results are shown in Figure 9.

As evident from Figure 9, proposed “Split and

Extended SIFT” outperforms the both other

considered ANN algorithms in speeding up of

features matching for all precision

degrees.

6 CONCLUSIONS

In this paper two novel ideas are proposed to

accelerate the matching process. Both ideas are

based on the same principle, which is comparison of

only features that share the same property which

may lead to correct matches. The proposed method

was compared with two algorithms for ANN

searching, hierarchical k-means and randomized kd-

trees. The presented experimental results show that

the performance of the proposed method

outperforms two other considered algorithms. Also,

the presented experimental results show that the

feature matching step can be accelerated 18 times

with respect to exhaustive search without losing a

noticeable portion of correct matches. When only

50% of correct matches is required, the speedup

factor can be increased to more than100.

REFERENCES

Chariot, A., Keriven, R., 2008. GPU- boosted online

image matching, 19th International Conference on

Pattern Recognition 1-4. IEEE

Bay, H., Tuytelaars, T., Van Gool, L., 2008. SURF:

Speeded Up Robust Features, Int. Journal of

Computer Vision and Image Understanding. Vol. 110,

Issue 3, 346-359

Firedman J.H., Bentley J.L. & Finkel R.A. 1977. An

algorithm for finding best matches in logarithmic

expected time. Transactions Mathematical Software.

ACM 209-226.

Harris, C., Stephens, M. 1988. A combined corner and

edge detector, International Conference of the Alvey

Vision Conference. 147-151.

Heymann, S., Miller, K., Smolic A., Froehlich B.,

Wiegand, T., 2007. SIFT implementation and

optiization for general-purpose GPU, In WSCG ’07.

Ke Y., Sukthankar, R., 2004. PCA-sift: A more distinctive

representation for local image descriptors. In Proc.

CVPR. USA. 506–513.

Lowe, D. G., 2004. Distinctive image features from scale

invariant keypoints. Int. Journal of Computer Vision

60(2), 91–110.

Martens, C., Prenzel, O., Gräser, A., 2007. The

Rehabilitation Robots FRIEND-I&II: Daily Life

Independency through Semi-Autonomous Task-

Execution; Rehabilitation. I-Tech Education

Publishing. Vienna, Austria. ISBN 978-3-902613-01-1

Mikolajczyk, K. Schmid, C., 2005. A performance

evaluation of local descriptors. IEEE Transactions on

pattern analysis and machine intelligence. VOL 27,

NO.10

Simon, M. K., Shihabi, M. M., Moon, T., 1995. Optimum

Detection of Tones Transmitted by a Spacecrft, TDA

PR 42-123, 69-98

Muja M. & Lowe D. G. 2009 Fast Approximate Nearest

Neighbors with Automatic Algorithm Configuration,

in International Conference on Computer Vision

Theory and Applications (VISAPP'09)

SPEEDED UP IMAGE MATCHING USING SPLIT AND EXTENDED SIFT FEATURES

295