MINIMUM SPANNING TREE FUSING MULTI-SALIENT POINTS

HIERARCHICALLY FOR MULTI-MODALITY IMAGE

REGISTRATION

Shaomin Zhang, Lijia Zhi, Dazhe Zhao and Hong Zhao

College of Information Science and Engineering, Northeastern University, Shenyang, Liaoning, China

Key Laboratory of Medical Image Computing (Northeastern University) Ministry of Education, China

Keywords: Medical Image Registration, Entropic Spanning Graph Estimator, Minimum Spanning Tree (Mst), Rényi

Entropy, Salient Point.

Abstract: In this paper, we propose a novel registration algorithm based on minimal spanning tree. There are two

novel aspects of the new method. First, instead of a single feature points, we extracted corner-like as well as

edge-like points from image, and also added a few random points to cover the low contrast regions; Second,

the hierarchical mechanism which fusing multi-salient points is used to drive the registration during the

registration procedure. The new algorithm has solved the low robustness brought by the instability of

extraction of feature points and the speed bottleneck problem when using MST to estimate the Rényi

entropy. Experiment results show that on the simulated and real brain datasets, the algorithm achieves better

robustness while maintaining good registration accuracy.

1 INTRODUCTION

Medical image registration is the basis of medical

image fusion, and has been used in medical

diagnosis, treatment, research, etc. Information-

theoretic metrics, such as Shannon entropy, Rényi

entropy, Tsallis entropy, etc, have been widely used

in medical image registration. Information-theoretic

metric are needed to estimate the entropy from the

image data. Currently, there are three types of

nonparametric entropy estimation methods: plug-in,

sample-spacings and entropic spanning graphs

estimator (Beirlant et al., 1997; Hero et al., 2002).

Plug-in estimator is simple, and suitable for low

dimensional space. But in high dimensional space, it

will encounter “dimension disaster” problem.

Sample-Spacings estimator was originally developed

for one- dimensional samples. Miller (Miller, 2003)

extended this technique to higher dimensions using

Voronoi regions and Delaunay triangulations.

Graph-based entropy estimators have faster

asymptotic convergence rates, especially for non-

smooth densities and for low dimensional feature

spaces; they completely bypass the complication of

choosing and fine tuning parameters; they can be

easily extended to higher dimensional space (Hero et

al., 2002). Redmond and Yukich (Redmond and

Yukich, 1996) proved that when a graph is “quasi-

additive” in d-dimensional feature space, d>=2, the

graph can be used to estimate the entropy directly.

Hero (Hero et al., 2002) pointed that among the

currently known quasi-additive algorithms, the MST

is the fastest (with polynomial run time) and applied

it to image registration.

On this basis, scholars have done relevant

research in the field of medical image registration

(Sabuncu and Ramadge, 2004, 2008) and found that

it will encounter speed bottleneck when using MST

to estimate the entropy. In order to make

constructing MST feasible for image registration

problem, appropriate features must be extracted to

compress the original great amount of data. Ma (Ma

et al., 2000) registered two images using uniform

sub-sampling. Sabuncu (Sabuncu and Ramadge,

2004) proposed two (deterministic and stochastic)

non-uniform sub-sampling methods for improving

the efficiency. But, uniform sub-sampling method

treats each pixel equally during the registration

procedure, regardless of whether some voxels are

more important than others in registration. Gradient

based sub-sampling method is sensitive to noise, and

feature points are of poor stability.

Zhang S., zhi L., Zhao D. and Zhao H. (2010).

MINIMUM SPANNING TREE FUSING MULTI-SALIENT POINTS HIERARCHICALLY FOR MULTI-MODALITY IMAGE REGISTRATION.

In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 33-36

DOI: 10.5220/0002820700330036

 SciTePress

In this paper, we propose a novel hierarchical

multi-modality registration algorithm which fusing

multi-salient points based on minimal spanning tree.

This new method not only considers multi- salient

points, but also considers hierarchical mechanism

during the registration procedure to improve the

robustness of the registration. Experimental results

showed that the new method has higher success rate

than single feature and uniformly sub-sample

methods based on minimum spanning tree on the

images from BrainWeb (Collins et al., 1998) and

Vanderbilt Retrospective Registration Project(RREP)

(West et al., 1997).

2 METHOD

2.1 Salient Point Extraction

Salient points contain structural and texture

information, which is important for image

registration. For example, the voxels that lie in the

region of interest or at the boundary of region are

more significant for image analysis. First, we

removed the background of the image by the

threshold of grey value. Second, similar to Harris

detector and Yang’s method (Harris and Stephens,

1988; Yang et al., 2007), we use auto-correlation

matrix as a single response measure to produce

potential corner like and edge like points. At each

pixel location x, the Auto-correlation matrix, μ is

computed,

11 12

21 22

() ()

() ()*

() ()

xxy

xy y

xLLx

Lx Lx

éù

êú

ëû

(1)

Where g is a Gaussian function with standard

deviation σ. L

is the derivative computed in the α

direction. λ1 and λ2 are the eigenvalues of μ.

Potential corners are at pixels where λ1 /λ2>0.1.

Potential edge points are at pixels for which λ1 /

λ2<=0.1. Finally, we got the corner like points and

the edge like points. The result is illustrated in Fig.1.

(a) Potential corner-like points (b) Potential edge-like points

Figure 1: Salient point extraction.

2.2 Hierarchical Registration

Mechanism

In section 2.1, we have got potential corner and edge

points. However, there are two problems in

constructing MST. First, the sum of corner and edge

points is so many, resulting in the speed bottleneck.

Second, many low-contrast regions are not covered

by any of salient points, resulting in much

registration errors. So we use hierarchically

mechanism, which was first proposed by Shen and

Davatzikos (Shen and Davatzikos, 2002), to select

salient points as the active points to drive the

registration during the registration procedure. To

make these points local adaptive, we divided the

image into 10*10 sub-regions. In each sub-region,

we sort the voxels by corner measure and edge

measure respectively.

Corner measure: cornerness = det(μ(x)) – α

trace

(μ(x));

Edge measure: edgeness = trace(μ(x));

In order to make the distribution of the active

points more uniform and the method more

robustness, we add some random points to cover the

low contrast regions. The hierarchical selection of

active points in three registration phases is showed

as follows:

 First phase: During the initial registration phase,

in each sub-region, the highest strength point of

the corner values is selected as active point. In

this way, we can also select edge point. If the

region doesn’t have any active points, we will

add two random points. If the region has only

one active point, we will add one random point

to the region.

 Second phase: With progress of registration,

those second strength potential corner and edge

points will be selected as active points to drive

the image registration, leading to the refinement

of registration results. If the region doesn’t have

enough active points, we will add random points

as first phase.

 Third phase: Finally, those third strength corner

and edge points will be considered as active

points for image registration. If the region

doesn’t have enough active points, we will add

random points as first phase.

In each registration phase, we will construct

MST on the active points.

2.3 Entropic Spanning Graph Estimator

Given V={P

∈

, i=1,…,n} of n vertices, a

spanning tree is a connected acyclic graph which

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

passes through every vertex. All n vertices are

connected by edges E={e

=( P

, P

)|i, j=1,…,n,

i≠j}. For a given edge weight exponent γ, the

minimum spanning tree is the spanning tree which

minimizes the total edge weight of the graph,

() | |

eMST







(2)

For a continuous pdf f, Rényi entropy H

(f) is

defined as,

() log ()

Hf fxdx









(3)

where α=(d-γ)/d.

Steele (Steele, 1998) has proved that the length

of the MST has the following asymptotic property,

()

lim ( )

xdx















(4)

Where β is a constant independent of f.

Combining (3) and (4), we obtain an estimator of

Rényi entropy from the total edge weight of the

MST,

1()

() [log log ]

1()

() log

µ

(5)

It follows directly from the results of Steele

(Steele, 1998) that the MST estimate



is a

strongly consistent estimator of H

3 EXPERIMENTAL RESULTS

(a) BrainWeb images

(b) RREP images

Figure 2: DataSets.

In this section, we present two sets of experiments.

The first set of experiments is used to test several

variations on the choice of salient points. The second

set is used to evaluate the performance of proposed

method, compared to traditional uniform sub-

sampling based multi-resolution image registration.

All experiments are tested on simulated and real 2D

MR brain images.

Figure 2(a) are the T1 and T2 MR brain images

with 5% noise and 20% intensity non- uniformity

obtained from the BrainWeb MR. Figure 2(b) are the

T1 and T2 MR brain images provided by RREP,

first of all, we register the two images by using their

fiducial markers, and then do the experiment.

3.1 Choice of Salient Points

T1 and T2 MR Brain images of the two datasets

were used to evaluate variations on the choice of the

salient points. T1 image is transformed by a angle

randomly generated from the different range of

degree, and two translations (T

， T

) from the

different range of pixels. For simulated BrainWeb

dataset, the range is [-15, 15] and [-20, 20], while for

the real RREP dataset, the range is [-10, 10] and [-15,

15]. Each dataset generates 50 randomly

transformed T1. Then the T2 image is registered to

the transformed T1. The registration is regarded as

success if the translation errors on both axes are

below 2 pixel and rotation error below 2 degree. The

success rates of all salient point- based registration

methods were listed in table 1.

Table 1: Comparison of the choice of the salient points.

DataSet Range

Success Rate (%)

Our

Corner-

only

Edge-

only

BrainWeb

[-15, 15] 98 88 82

[-20, 20] 84 84 70

RREP

[-10, 10] 100 92 98

[-15, 15] 72 68 68

From Table 1, we can conclude that this

combination of multi-salient points performed better

than both methods alone for two test datasets.

Particular for BrainWeb image with 5% noise and

20% intensity non- uniformity dataset, the

performance of the edge-based method is lower than

our method due to the edge-base method is more

sensitive to noise.

3.2 Comparison of Registration

Methods

Similar to section 3.1, the success rates of our

propose method and uniform sub-sampling based

method was calculated and listed in Table 2. It is

MINIMUM SPANNING TREE FUSING MULTI-SALIENT POINTS HIERARCHICALLY FOR MULTI-MODALITY

IMAGE REGISTRATION

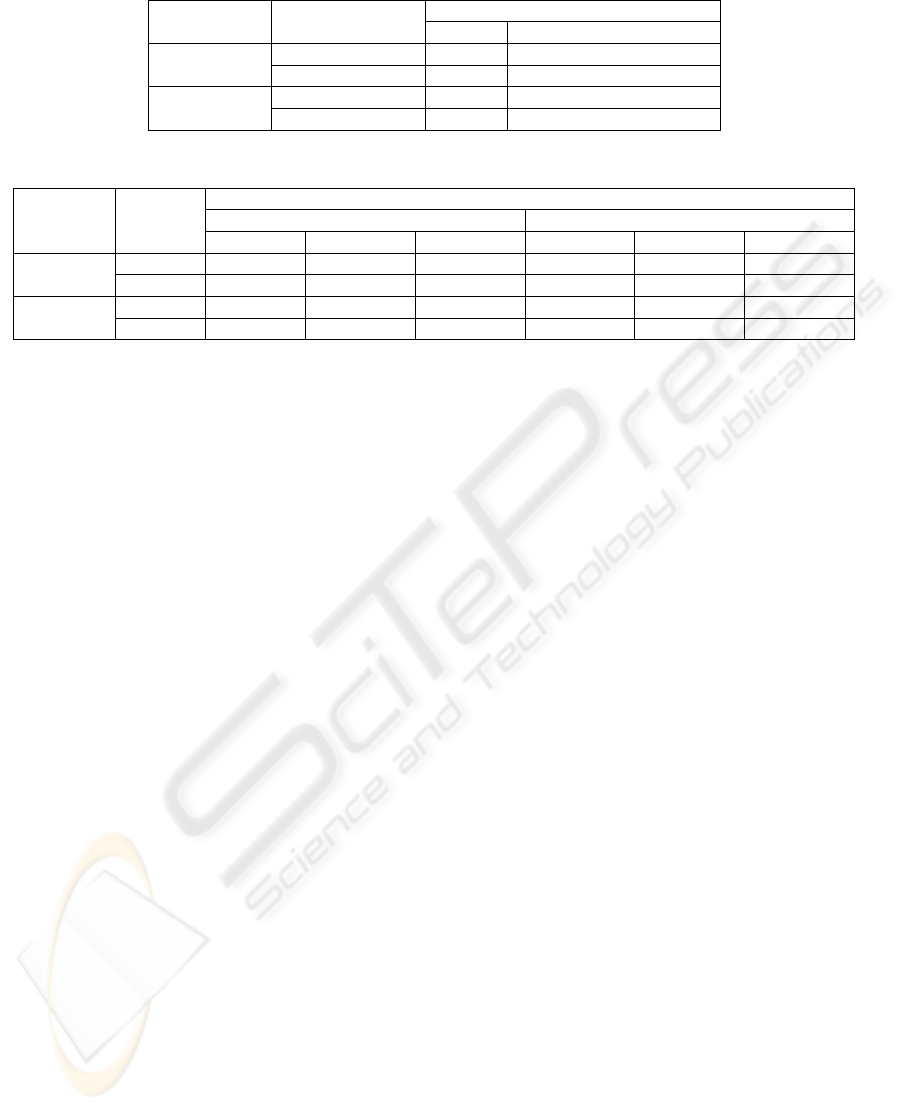
Table 2: Comparison of registration methods.

DataSet Range

Success Rate (%)

Our Uniform sub-sampling

BrainWeb

[-15, 15] 98 96

[-20, 20] 84 86

RREP

[-10, 10] 100 70

[-15, 15] 72 58

Table 3: Comparison of means and standard deviations of registration errors.

DataSet Range

Mean and Standard deviation

Our Uniform sub-sampling based

Tx Ty Rz Tx Ty Rz

BrainWeb

[-15, 15] 0.27±0.17 0.21±0.16 0.20±0.17 0.25±0.17 0.16±0.11 0.21±0.14

[-20, 20] 0.21±0.14 0.19±0.15 0.20±0.14 0.27±0.17 0.16±0.14 0.23±0.17

RREP

[-10, 10] 0.66±0.43 0.58±0.43 0.66±0.32 1.03±0.56 0.59±0.43 0.51±0.45

[-15, 15] 0.93±0.57 0.79±0.58 0.69±0.34 0.93±0.54 0.58±0.49 0.47±0.36

clearly that the proposed method outperformed

traditional uniform sub-sampling based method.

For those successful cases of registration, mean

and standard deviations of rotation errors and

translation errors were calculated and summarized in

Table 3. We can observe that the accuracy of our

proposed method is comparable to that of uniform

sub-sampling based method.

4 CONCLUSIONS

In this paper, we have presented a novel method of

constructing minimal spanning tree for multi-

modality image registration. The new method

hierarchically fuses multi-salient points to construct

MST. This new method integrates not only more

information obtained from multi-salient points to

improve robustness of image registration, but also

hierarchical mechanism to produce relatively

accurate registration results. Experiment results

show that on the simulated and real brain datasets,

the algorithm achieves better robustness while

maintaining good registration accuracy.

REFERENCES

Beirlant, J., Dudewicz, E. J., Gyorfi, L., and van der

Meulen, E.C. (1997). Nonparametric entropy

estimation: An overview. International Journal of

Mathematical and Statistical Sciences, 6(1):17–39.

Collins,D.L., Zijdenbos,A.P., Kollokian,V., Sled, J.G.,

Kabani, N.L., Holmes, C.J., and Evans, A.C. (1998).

Design and construction of a realistic digital brain

phantom. IEEE Trans. Med. Imag., 17:463-468.

Harris, C., Stephens, M. (1988). A Combined Corner and

Edge Detector. In Alvey Vision Conference, pages

147-151.

Hero, A., Ma, B., Michel, O., and Gorman, J. (2002).

Applications of entropic spanning graphs. IEEE Signal

Processing Magazine, 19(5):85–95.

Ma, B., Hero, A., Gorman, J., and Michel, O. (2000).

Image registration with minimal spanning tree

algorithm. In ICIP.

Miller, E. (2003). A new class of entropy estimators for

mult-dimensional densities. In Proc. ICASSP.

Redmond, C., Yukich, J. (1996). Asymptotics for

Euclidean functionals with power weighted edges.

Stochastic Processes and their Applications,

61(2):289-304.

Sabuncu, M. R., Ramadge, P.J. (2004). Gradient based

nonuniform subsampling for information-theoretic

alignment methods. In EMBC.

Sabuncu, M. R., Ramadge, P. J. (2008). Using Spanning

Graphs for Efficient Image Registration. IEEE

Transactions on Image Processing, 17(5):788-797.

Shen, D., Davatzikos, C. (2002). HAMMER: hierarchical

attribute matching mechanism for elastic registration.

IEEE Trans. Med. Imaging, 21(11): 1421–1439.

Steele, J. M. (1988). Growth rate of Euclidean minimal

spanning trees with power weighted edges. Ann.

Probab., pages 1767–1787.

West, J., Fitzpatrick, J.M., Wang, M.Y., Dawant, B.M.,

Maurer Jr., C.R., Kessler, R.M., Maciunas, R.J.,

Barillot, C., Lemoine, D., Collignon, A., Maes, F.,

Suetens, P., Vandermeulen, D., van den Elsen, P.A.,

Napel, S., Sumanaweera, T.S., Harkness, B., Hemler,

P.F., Hill, D.L.G., Hawkes, D.J., Studholme, C.,

Maintz, J.B., Viergever, M.A., Malandain, G., and

Woods, R.P. (1997). Comparison and evaluation of

retrospective intermodality brain image registration

techniques. J. Comput. Assist. Tomogr, (4):554–566.

Yang, G., Stewart, C., Sofka, M., Tsai C. (2007).

Registration of challenging image pairs: initialization,

estimation, and decision. IEEE Trans. Pattern Anal.

Mach. Intell., 29(11):1973-1989.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications