VIEWPOINT ENTROPY-DRIVEN SIMPLIFICATION METHOD

FOR TEXTURED TRIANGLE MESHES

Carlos González, Pascual Castelló, Miguel Chover

Universitat Jaume I, Castellón, Spain

Mateu Sbert, Miquel Feixas

Universitat de Girona, Girona, Spain

Keywords: Mesh Simplification, Texture Preservation.

Abstract: This paper proposes a viewpoint-driven simplification method for textured triangle meshes. Models used in

interactive applications are usually composed of geometric meshes with textures. Thus, textures play an

important role in the final aspect of the simplified models. This method considers the texture shape in the

error metric. Entropy, a concept from Information Theory, is used in this error metric. We show in the

experiments that this method produces simplifications that preserve textures better than the methods that do

not take them into account. Therefore, great distortions when applying the textures are avoided.

1 INTRODUCTION

Models used in interactive applications, like games,

are usually composed of geometric meshes with

textures. Nowadays, 3D scenes tend to present

models composed of a great number of polygons.

But in this kind of application the time required to

process the scene is a crucial point. And the graphic

hardware cannot always handle all this geometry

with a high frame-rate.

One of the solutions presented was the use of

simplification methods. Simplification methods

allow us to avoid storing and processing all the

geometry of the objects in the scene. This introduced

a great advance in interactive applications. The

result of simplifying an object is another object with

less geometry. This fact reduces the GPU load.

Simplification methods try to produce simplified

objects with a similar appearance to the original

ones.

We can distinguish between different

simplification methods, depending on their

simplification criteria. A survey of polygonal

simplification algorithms can be found in (Luebke,

2001). Many simplification methods are only based

on the geometry of the objects. These methods try to

generate good geometric results on the simplified

object (for example, criteria based on co-planarity).

Other methods are based on the visual appearance.

These methods try to produce not only good

geometry results, but also realistic results for the

viewer, by, for example, removing first parts of the

object that are not visible for the user

Not only final geometry is important in the

simplified objects. Models used in interactive

applications usually have additional attributes to

their geometry, such as textures. This kind of mesh

needs to present the simplified models with a good

aspect. Textures play an important role on their

appearance. Therefore, good textured models must

be presented in the scene.

A simplification method makes use of an error

metric and a simplification operation. The error

metric will establish the order in which the

simplifications steps will be performed. And the

simplification operation will define how the

geometry of the models will be simplified. There are

not many simplification methods that consider

texture information in the error metric. If texture

information is not taken into account in the error

metric, the order of the simplification steps will be

established without considering the texture of the

model. Therefore, simplified objects can present a

great distortion when the texture is applied. This will

produce unsuitable simplified models to be shown in

interactive applications.

González C., Castelló P., Chover M., Sbert M. and Feixas M. (2010).

VIEWPOINT ENTROPY-DRIVEN SIMPLIFICATION METHOD FOR TEXTURED TRIANGLE MESHES.

In Proceedings of the International Conference on Computer Graphics Theory and Applications, pages 30-37

DOI: 10.5220/0002820800300037

 SciTePress

A solution to this problem is presented in this

paper. Here we present a new simplification method

for triangle meshes that takes texture shapes into

account in its error metric.

The presented method is a viewpoint-driven

simplification method and uses edge collapse

operation. An edge collapse is a simplification

operation that removes edges by merging the

vertices of the edges. The final vertex can be placed

at one of the original vertices (half-edge collapse) or

can be moved to other spatial coordinates. Figure 1

shows an example of a half-edge collapse operation.

Figure 1: The half-edge collapse operation.

Our method is a viewpoint-driven simplification

method. Therefore, we use some cameras around the

object in order to obtain the cost associated to each

edge. These associated costs will give us the

simplification order. In order to take the texture

information into account, we use an image

segmentation method. This will produce another

image with different colored regions. Considering

texture information, edge collapses that produce a

great change in the texture will have a high

associated cost. Therefore, we penalize those edges

that their collapse can produce great distortions in

the final aspect of the model.

The main steps of this method are:

 The segmentation of the texture image,

generating a new image with some colored

regions.

 The calculation of the initial costs associated to

the edges of the model. This will take into

account the information obtained after the

segmentation step.

 The simplification algorithm. After each

simplification step, some costs will be recalcu-

lated. This will also consider the segmentation

information.

The rest of this paper is structured as follows. In

Section 2 we describe the background to this

research. In Section 3 we explain the method in

detail. Section 4 shows some results and in Section 5

we discuss the conclusions.

2 BACKGROUND

During the last years, a lot of simplification methods

have been developed. Automatic simplification

methods avoid designers to perform elaborate

reduction processes. A survey of simplification

methods for polygonal models can be found in

(Luebke, 2001). Some works on user-assisted

simplifications can also be found in the literature

((Kho and Garland, 2003), (González et al., 2009)).

But there are not many simplifications methods that

produce good textured results. A background of

simplification methods for triangular meshes that

consider attributes, like textures, is exposed here.

Cohen et al. (1998) presented a method that

parameterises the model in order to obtain the texels,

obtaining some patches of the surface. Texture

deviation metric is used to calculate the cost of the

pairs. At each simplification step this metric is

calculated for the modified faces. It also preserves

the boundaries.

Garland and Heckbert (1998) improved their

method (Garland and Herbert, 1997) by extending

the quadrics, taking into account the properties of

the model. It also preserves the boundaries, a high

collapse cost being assigned to these edges.

Hoppe (1999) introduced a new quadric metric

for simplifying meshes while taking attributes into

consideration.

Lindstrom and Turk (2000) introduced a pure

image-based metric. The main advantage of this

image metric is that it allows the texture attributes to

be taken into account, while also measuring the error

made in edge collapse.

Luebke and Hallen (2001) presented a method

for performing a view-dependent polygonal

simplification using perceptual metrics. These

metrics derive from a measure of low-level

perceptibility of visual stimuli in humans. Later

Williams et al. (2003) extended this work for lit and

textured meshes.

Sander et al. (2001) presented a method that

extended the work introduced in (Hoppe, 1996).

This method subdivides the surface into patches, on

the grounds of its coplanarity. It then generates a

parameterisation by minimizing the stretch

deviation. It calculates an adequate size for each

VIEWPOINT ENTROPY-DRIVEN SIMPLIFICATION METHOD FOR TEXTURED TRIANGLE MESHES

object in the texture domain and simplifies the mesh

by minimising the texture deviation (Cohen et al.,

1998) and preserving the boundaries. Finally, it

optimizes the parameterization with a different

objective function and regroups all the patches

again.

Zhang and Turk (2002) proposed a new

algorithm that takes visibility into account. Their

approach defined a visibility function between the

surfaces of a model and a surrounding sphere of

cameras. In order to guide the simplification process,

they combined their visibility measure with the

quadric measure introduced by Garland and

Heckbert (1997).

Shao et al. (2004) presented a method that takes

geometric and texture information into account in

the error metric. Thus, the edge cost is defined as a

combination of the geometric error metric and the

texture error metric.

Lee et al. (2005) introduced the idea of mesh

saliency as a measure of regional importance for

graphics meshes. Basically, their approach consists

in generating a saliency map and then simplifying by

using this map in the QSlim algorithm as in (Zhang

and Turk, 2002). The new edge collapse cost is that

of the quadric multiplied by the saliency of this

edge.

Garland and Zhou (2005) presented a method for

simplifying simplicial complexes of any type

embedded in Euclidean spaces of any dimension.

Both the geometry of the object and also the

texture frequencies were considered in (Xu et al.,

2005). To make the method more precise, pixels are

subdivided into subpixels.

The method presented in (Chen and Chuang,

2006) recalculates a new texture for each

simplification step, an indexing map being used to

avoid loss of precision.

González et al. (2007) presented an error metric

extension to take texture information into account in

those methods that do not consider it. This extension

is based on the calculation of the borders of the

texture. Then, the cost of those edges that intersect

these borders is modified, by adding the relative area

of the triangles that share this edge. This way, edges

that cross any particular border in the texture are

penalized, and they will be simplified later than

before applying the extension.

González et al. (2008) proposed a simplification

method that considers the possibility of duplicated

vertices in meshes usually used in interactive

applications.

3 SIMPLIFICATION METHOD

The simplification method is a viewpoint-driven

simplification method based on edge collapse

operation. Its metric makes use of the texture

segmentation information to assign the cost

associated to each edge of the model.

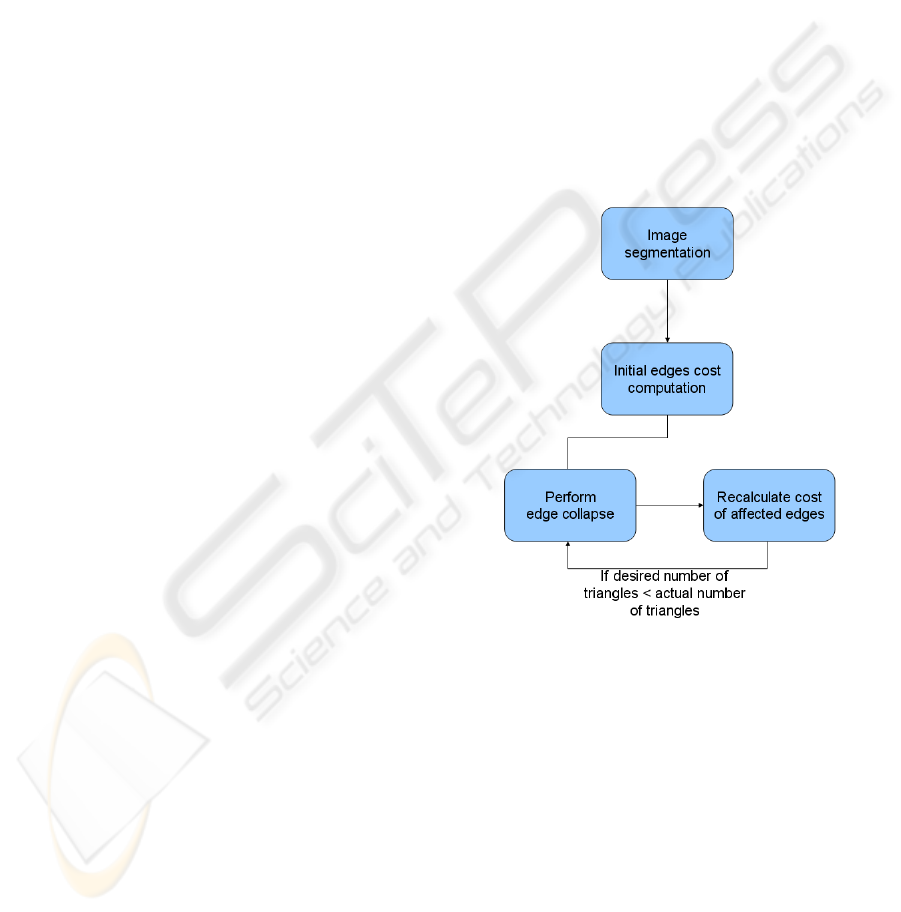
The main parts of the method are the

segmentation of the texture image, the initial

computation of edge costs and the iterative

simplification process. A general workflow of the

method is shown in Figure 2. In this figure, it can be

seen that we first perform the segmentation of the

texture image of the model. After this, we calculate

the cost associated to edge by using viewpoint

entropy as the error metric. And finally, we perform

the iterative simplification process, recalculating the

costs of some specific edges in the affected regions.

Figure 2: General workflow of the method.

The process is explained in detail in the next

subsections (3.1, 3.2 and 3.3).

3.1 Texture Regions

The presented method considers texture shape in its

metric. The algorithm of simplification will produce

simplified models considering the shape of the

texture applied on them. This way, great dis-

tortions in the applied texture of simplified models

will be avoided.

We divide the textures into regions. To do this,

we perform a segmentation of the texture image. We

use the method presented in (Felzenszwalb and

Huttenlocher, 2004). With this method, a new image

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

with the different regions of the texture colored is

obtained. Additionally, we have modified the color

selection in order to have a different color for each

region. Therefore, we can identify each region with

a unique color.

Figure 3 shows the segmentation of a texture

image. This method accept different parameters,

such as



(parameter of a Gaussian distribution

used in the segmentation process) and

k (useful to

compute a defined threshold function). Depending

on the value of these parameters, we will obtain

different segmentation results (see (Felzenszwalb

and Huttenlocher, 2004)).

Figure 3: Original texture of a toonturtle model (left) and

the image after the segmentation process (right).

3.2 Error Metric

3.2.1 Entropy

During the last years some authors have combined

the idea of some mathematical measures of

similarity with simplification methods ((Lindstrom

and Turk, 2000), (Castelló et al., 2008)). The results

presented in (Castelló et al., 2007) proved that this

kind of measure can be used with efficiency in the

context of polygonal simplification.

The entropy is a measure of information that

measures the uncertainty associated with a random

variable. That is, the entropy represents the average

information content missed when the value of the

random variable is unknown. This concept was

introduced by Shannon (1948). Mathematically, the

entropy

)(XH of a discrete random variable

with values in the set

},...,,{

21 n

xxxS  is

defined as:







ppXH

)log()(

(1)

where the base of the logarithm is 2 (entropy is

expressed in bits),

n is the number of elements,



xXp  Pr for



ni ,...,1



and )0log(0

is taken to be

0 .

The situation of the maximum uncertainty is

produced when all the possible values have the same

probability. For example, if we have

n possible

values for a variable the maximum uncertainty is

given when all of these values have an associated

probability of

Some properties of the entropy are:



)log()(0 nXH



0)(



XH if and only if all the probabilities

except one are zero and this exception has a

value of unity, i.e., when we are certain of the

outcome.

)log()( nXH



when all the probabilities are

equal. This is the most uncertain situation.

 If we equalize the probabilities, entropy

increases, that is, the maximum entropy is

reached when all probabilities are equal and their

value is

3.2.2 Viewpoint Entropy

Viewpoint entropy was defined in (Vázquez, 2001)

from the relative area of the polygons projected over

the sphere of directions centered at viewpoint

Thus, viewpoint entropy was defined by:

log







(2)

where

N is the number of polygons of the

scene,

a is the area of the polygon i projected over

the sphere,

a represents the projected area of the

background in open scenes, and





is the

total area of the sphere. Maximum entropy is

obtained when a certain viewpoint can see all the

polygons with the same projected area. The best

viewpoint is defined as the one that has maximum

entropy.

3.2.3 Region Entropy

By applying the image obtained after the

segmentation process to the object, we can calculate

the relative area of the regions projected over the

VIEWPOINT ENTROPY-DRIVEN SIMPLIFICATION METHOD FOR TEXTURED TRIANGLE MESHES

sphere of directions centered at viewpoint

v .

Therefore, region viewpoint entropy is defined by:

log







(3)

where

N is the number of regions in the

segmentation image,

ar is the area of the region i

projected over the sphere,

ar represents the

projected area of the background in open scenes, and





arar

is the total area of the sphere.

Maximum entropy is obtained when a certain

viewpoint can see all the regions with the same

projected area. The best viewpoint is defined as the

one that has maximum entropy.

3.3 Simplification Steps

The simplification process is divided into two main

steps: the initial edge cost computation (Subsection

3.3.1) and the iterative simplification process

(Subsection 3.3.2).

3.3.1 Initial Edge Cost Computation

We perform an initial edge cost computation in

order to assign a cost to each edge. This will

establish the order of the edge collapse operations.

The associated cost of an edge represents how the

regions are going to change after the collapse of this

edge. The edges with high associated costs will be

collapsed in the last simplification steps. Therefore,

the edges collapsed first will be those that will

produce less change in the texture regions. This way,

the method collapses first the edges that will

produce less distortion in the texture aspect in the

simplified model.

The background is considered as another region.

Thus, models will also maintain their external

geometric appearance by giving high costs to those

edges that their collapse will produce a great

distortion in the silhouette of the model. We use a

histogram to calculate the projected area of

each region for each camera.

We consider the error produced in all the

cameras in order to compute the edge costs.

Therefore, we define the cost associated to each

edge as the sum of the differences before

simplifying and after simplifying of the region

viewpoint entropies. That is,









rvrve

HHc

(4)

In order to assign the initial cost associated to

each edge, the method works as follows:

 Step 1. Locate some cameras around the object.

The distribution of these cameras is based on

platonic solids. That is, we place a camera to one

of the vertices of the selected platonic solid (for

example, an icosahedron will produce 12

cameras and a dodecahedron will produce 20

cameras). The cameras will look at the center of

the sphere formed by the solid. We have used 20

cameras. This number of cameras has been used

in methods in the literature ((Lindstrom and

Turk, 2000), (Castelló et al., 2008)).

 Step 2. Render the model in the center of the

sphere. The texture image obtained after the

segmentation process is applied on it. See Figure

 Step 3. Calculate the initial

H for the model

textured with the segmented texture image.

 Step 4. Perform an edge collapse without an

associated cost (initially, there is no edge with an

associated cost).

 Step 5. Calculate the actual

H and assign the

difference with the original

H to the collapsed

edge.

 Step 6. Undo the edge collapse.

 Step 7. Until all the edges have an associated

initial cost, go to Step 4.

Figure 4 shows an example of a model textured

with the image obtained after the segmentation of its

texture. Some cameras are located around the model.

Figure 4: Model textured with the segmented texture

image and cameras around it.

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

3.3.2 Iterative Simplification Process

After assigning the initial collapse costs to all the

edges in the model, the method will perform an

iterative simplification process.

Normally, the level of simplification is indicated

as the number of desired final faces. The method has

a count of the faces in the model at each moment.

Therefore, the simplification process will be

performed until the desired level of simplification is

obtained.

Edges are collapsed in the order given by their

associated cost. Edges with a low associated cost

will be collapsed before than edges with a high

associated cost.

After collapsing an edge, the cost of some edges

must be recalculated. These edges are the ones that

are adjacent to the vertices adjacent to the vertex

resulting from a collapse. This is because the regions

of the texture applied on the model, may change

when the geometry is altered. To do this, we create a

viewport from each camera in order to analyze only

these edges. Therefore, we avoid recalculating the

cost of all the edges in the model again.

The iterative simplification process works as

follows:

 Step 1. Extract the edge

with the lowest

associated cost.

 Step 2. Perform collapse of

 Step 3. Retriangulate the affected faces.

 Step 4. Recalculate cost of the affected faces.

 Step 5. While the number of faces if greater than

the desired number of faces, go to Step 1.

4 RESULTS

Several models have been tested with the presented

method. Some results are now depicted and

commented. We present the results compared to

another simplification method (Castelló et al., 2007)

that works similar, but without taking textures into

account. The method presented by Castelló et al.

(2007) is a viewpoint-driven simplification method

that uses the entropy concept with the distribution of

the projected areas of the polygons of the model.

The main difference is that the presented method

works with the distribution of the regions obtained

in the texture images.

Some simplifications of three models are exposed in

Figures 5, 6 and 7. We compare our simplification

results with the simplifications obtained by the

method presented in (Castelló et al., 2007). Figure 5

Figure 5: Original tank model (subfigure a), tank model

simplified to 10% without considering textures (subfigure

b) and tank model simplified to 10% with our method

(subfigure c).

Figure 6: Original head model (a), simplifications of the

head model to 70%, 50% and 25% without considering

textures (b, c and d) and with our method (e, f and g).

VIEWPOINT ENTROPY-DRIVEN SIMPLIFICATION METHOD FOR TEXTURED TRIANGLE MESHES

Figure 7: Original swimmer model (subfigure a) and simplifications to 35% without considering textures (subfigure b) and

with our method (subfigure c).

shows two different simplifications (to 10% and

5%) of the tank model (2,991 triangles). Three

different simplifications (to 70%, 50% and 25% of

the original geometry) of the head model (2,872

triangles) are depicted in Figure 6. Figure 7 shows

a simplification to 35% of the swimmer model

(4,130 triangles). It can be seen that our method

preserves textures more accurate than the methods

that do not take texture information into account.

The temporal cost of this method is similar to

the temporal cost obtained in other viewpoint-

driven simplification methods. We state this

because the main difference is the way of

computing the error metric, which is the

calculation of simple mathematical operations.

Moreover, the texture image segmentation is a fast

process. It depends on the resolution of the texture

and it can be considered as a pre-process.

5 CONCLUSIONS

We have presented a new viewpoint entropy-

driven simplification method for textured triangle

meshes. Interactive applications, like games, tend

to present models with a well-textured appearance.

Therefore, textures play an important role in this

kind of application.

Simplification methods allow the applications

to present models with less geometry, reducing the

GPU load. There are not many simplification

methods that consider texture information during

the simplification process. If this information is not

taken into account, simplified models with great

distortions in their texture appearance can be

produced. This method considers texture

information in its error metric. This allows

presenting simplified models with a more accurate

texture appearance than with simplification

methods that do not consider this information.

Moreover, a well-known mathematical concept

(entropy) has been used to formulate the error

metric.

The exposed results show the improvement in

the texture appearance of the simplified models

using this method, compared with the methods that

do not consider texture information for simplifying

the objects.

This method presents similar temporal costs

than other viewpoint-driven simplification methods

in the literature.

ACKNOWLEDGEMENTS

This work has been supported by the Spanish

Ministry of Education and Science (TIN2007-

68066-C04-02, TIN2007-68066-C04-01), Caja

Castellón-Bancaja Foundation (P1-1B2007-56)

and the Jaume I University (PREDOC/2005/12).

REFERENCES

Castelló P., Sbert M., Chover M., Feixas M., 2007.

Viewpoint entropy-driven simplification. 15th

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

International Conference in Central Europe on

Computer Graphics, Visualization and Computer

Vision (WSCG 2007), volume 2, 249-256.

Castelló P., Sbert M., Chover M., Feixas M., 2008.

Viewpoint-based simplification using f-divergences.

Information Sciences, 178 (11), 2375-2388.

Chen C.-C., Chuang J.-H., 2006. Texture Adaptation for

Progressive Meshes. Eurographics06-Geometry

Compression and Decompression.

Cohen J., Olano M., Manocha D., 1998. Appearance-

Preserving Simplification. Proceedings of ACM.

SIGGRAPH 98. 115-122.

Felzenszwalb P. F., Huttenlocher D. P., 2004. Efficient

Graph-Based Image Segmentation. International

Journal of Computer Vision, Volume 59, Number 2.

Garland M., Heckbert P. S., 1997. Surface Simplification

Using Quadric Error Metrics. Computer Graphics

(SIGGRAPH 97 Proceedings), 209-218.

Garland M., Heckbert P. S., 1998. Simplifying Surfaces

with Color and Texture Using Quadric Error

Metrics. Ninth IEEE Visualization 1998 (VIS'98),

264.

Garland M., Zhou Y., 2005. Quadric-based

Simplification in any Dimension. ACM Transactions

on Graphics, 24(2). Draft preprint available as Tech

Report UIUCDCS-R-2004-2450.

González C., Castelló P., Chover M., 2007. A texture-

based Metric Extension for Simplification Methods.

2nd International Conference on Computer Graphics

Theory and Applications (GRAPP 2007), 69-76.

González C., Gumbau J., Chover M., Castelló P., 2008.

Mesh simplification for interactive applications. In

WSCG’08 Proceedings, 87-94.

González C, Gumbau J, Chover M, Ramos F, Quirós R.,

2009. User-assisted simplification method for

triangle meshes preserving boundaries. Computer-

Aided Design 2009, Elsevier;41(12):1095-1106.

Hoppe H., 1996. Progressive Meshes. Computer

Graphics (Proc. Siggraph 96), vol. 30, ACM Press,

New York, 99-108.

Hoppe H., 1999. New Quadric Metric for Simplifying

Meshes with Appearance Attributes, Proc. IEEE

Visualization 99, IEEE CS Press, Los Alamitos,

Calif., pp. 59-66.

Kho Y, Garland M., 2003. User-guided simplification.

Proceedings of the 2003 symposium on Interactive

3D graphics, 123-126

Lee C.H., Varshney A., Jacobs D.W., 2005. Mesh

saliency. ACM Trans. Graph. 24, 3, pp. 659-666.

Lindstrom P., Turk G., 2000. Image-driven

simplification. ACM TOG 19, 3, 204-241.

Luebke D.P., 2001. A developer's survey of polygonal

simplification algorithms. IEEE Computer Graphics

and Applications 2001;21(3):24-35.

Luebke D.P., Hallen B., 2001. Perceptually-driven

simplification for interactive rendering. Proc. of the

12th Eurographics Workshop on Rendering

Techniques (London, UK), 223-234.

Sander P., Snyder J. Gortler S., Hoppe H., 2001.Texture

mapping progressive meshes. Proc. SIGGRAPH,

409-416.

Shannon C. E., 1948. A Mathematical Theory of

Communication. CSLI Publications.

Shao Y., Liu B., Zhang H., 2004. Geometry and texture

based simplification of 3D meshes. In ICSP’04

Proceedings, 1310-1313.

Vázquez P. P., Feixas M., Sbert M., Heidrich W., 2001.

Viewpoint selection using viewpoint entropy. In

VMV '01: Proceedings of the Vision Modeling and

Visualization Conference, 273-280.

Williams N., Luebke D., Cohen J.D., Kelley M.,

Schubert B., 2003. Perceptually guided

simplification of lit, textured meshes. Proc. of the

2003 symposium on Interactive 3D graphics (New

York, NY, USA), ACM Press, 113-121.

Xu A., Sun S., Xu K., 2005. Texture Information Driven

Triangle Mesh Simplification. Computer Graphics

and Imaging, 43-48.

Zhang E., Turk G., 2002. Visibility-guided

simplification. Proc. of IEEE Visualization 2002,

vol.31, 267-274.

VIEWPOINT ENTROPY-DRIVEN SIMPLIFICATION METHOD FOR TEXTURED TRIANGLE MESHES