
SHAPE FROM SHADINGS UNDER PERSPECTIVE PROJECTION
AND TURNTABLE MOTION
Miaomiao Liu and Kwan-Yee K. Wong
Department of Computer Science, The University of Hong Kong, Pokfulam, Hong Kong
Keywords:
Two-frame-theory, Shape recovery, Turntable motion.
Abstract:
Two-Frame-Theory is a recently proposed method for 3D shape recovery. It estimates shape by solving a first
order quasi-linear partial differential equation through the method of characteristics. One major drawback of
this method is that it assumes an orthographic camera which limits its application. This paper re-examines the
basic idea of the Two-Frame-Theory under the assumption of a perspective camera, and derives a first order
quasi-linear partial differential equation for shape recovery under turntable motion. Dynamic programming is
used here to provide the Dirichlet boundary condition. The proposed method is tested against synthetic and
real data. Experimental results show that perspective projection can be used in the framework of Two-Frame-
Theory, and competitive results can be achieved.
1 INTRODUCTION
Shape recovery is a classical problem in computer
vision. Many constructive methods have been pro-
posed in the literature. They can generally be classi-
fied into two categories, namely multiple-view meth-
ods and single-view methods. Multiple-view meth-
ods such as structure from motion (Tomasi, 1992)
mainly rely on finding point correspondences in dif-
ferent views, whereas single-view methods such as
photometric stereo use shading information to recover
the model.
Multiple-view methods can be further divided into
point-based methods and silhouette-based methods.
Point-based methods are the oldest technique for 3D
reconstruction (Pollefeys et al., 2001). Once feature
points across different views are matched, the shape
of the object can be recovered. The major draw-
back of such methods is that they depend on find-
ing point correspondences between views. This is
the well-known correspondence problem which itself
is a very tough task. Moreover, point-based meth-
ods do not work for featureless object. On the other
hand, silhouette-based methods are a good choice for
shape recovery of featureless object. Silhouettes are
a prominent feature in an image, and they can be ex-
tracted reliably even when no knowledge about the
surface is available. Silhouettes can provide rich in-
formation for both the shape and motion of an object
(Wong and Cipolla, 2001; Liang and Wong, 2005).
Nonetheless, only sparse 3D points or a very coarse
visual hull can be recovered if the number of images
used for reconstruction is comparatively small. Pho-
tometric stereo, which is a single-view method, uses
images taken from one fixed viewpoint under at least
three different illumination conditions. No image cor-
respondences are needed. If the albedo of the ob-
ject and the lighting directions are known, the surface
orientations of the object can be determined and the
shape of the object can be recovered via integration
(Woodham, 1980). However, most of the photometric
stereo methods consider orthographicprojection. Few
works are related to perspective shape reconstruction
(Tankus and Kiryati, 2005). If the albedo of the ob-
ject is unknown, photometric stereo may not be feasi-
ble. Very few studies in the literature use both shading
and motion cues under a general framework. In (Jin
et al., 2008), the 3D reconstruction problem is formu-
lated by combining the lighting and motion cues in
a variational framework. No point correspondences
is needed in the algorithm. However, the method in
(Jin et al., 2008) is based on optimization and requires
piecewise constant albedo to guarantee convergence
to a local minimum. In (Zhang et al., 2003), Zhang
et al. unified multi-view stereo, photometric stereo
and structure from motion in one framework, and
achieved good reconstruction results. Their method
has a general setting of one fixed light source and one
camera, but with the assumption of an orthographic
camera model.
28
Liu M. and K. Wong K. (2010).
SHAPE FROM SHADINGS UNDER PERSPECTIVE PROJECTION AND TURNTABLE MOTION.
In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 28-35
DOI: 10.5220/0002821300280035
Copyright
c
SciTePress

Similar to (Jin et al., 2008) , the method in (Zhang
et al., 2003) also greatly depends on optimization. A
shape recovery method was proposed in (Moses and
Shimshoni, 2006) by utilizing the shading and mo-
tion information in a framework under a general set-
ting of perspective projection and large rotation an-
gle. Nonetheless, it requires that one point correspon-
dence should be known across the images and the ob-
ject should have an uniform albedo.
A Two-Frame-Theory was proposed in (Basri and
Frolova, 2008) which models the interaction of shape,
motion and lighting by a first order quasi-linear par-
tial differential equation. Two images are needed to
derive the equation. If the camera and lighting are
fully calibrated, the shape can be recoveredby solving
the first order quasi-linear partial differential equa-
tion with an appropriate Dirichlet boundary condition.
This method does not require point correspondences
across different views and the albedo of the object.
However, it also has some limitations. For instance,
it assumes an orthographic camera model which is a
restrictive model. Furthermore, as stated in the paper,
it is hard to use merely two orthographic images of an
object to recover the angle of out-of-plane rotations.
This paper addresses the problem of 3D shape re-
covery under a fixed single light source and turntable
motion. A multiple-view method that exploits both
motion and shading cues will be developed. The fun-
damental theory of the Two-Frame-Theory will be re-
examined under the more realistic perspective camera
model. Turntable motion with small rotation angle is
considered in this paper. With this assumption, it is
easy to control the rotation angle compared to the set-
ting in (Basri and Frolova, 2008). A new quasi-linear
partial differential equation under turntable motion is
derived, and a new Direchlet boundary condition is
obtained using dynamic programming. Competitive
results are achieved for both synthetic and real data.
This paper is organized as follows: Section 2 de-
scribes the derivation of the first order quasi-linear
partial differential equation. Section 3 describes how
to obtain the Dirichlet boundary condition. Section 4
shows the experimental results for synthetic and real
data. A brief conclusion is given in Section 5.
2 FIRST ORDER QUASI-LINEAR
PDE
Turntable motion is considered in this paper. Simi-
lar to the setting in (Basri and Frolova, 2008), two
images are used to derive the first order quasi-linear
partial differential equation (PDE). Suppose that the
object rotates around the Y-axis by a small angle. Let
X = (X,Y,Z) denotes the 3D coordinates of a point
on the surface. The projection of X in the first im-
age is defined as λ
i
¯
x
i
= P
i
¯
X, where P
i
is the projec-
tion matrix,
¯
X is the homogenous coordinates of X
and
¯
x
i
is the homogenous coordinates of the image
point. Similarly, the projection of X after the rota-
tion is defined as λ
j
¯
x
j
= P
j
¯
X, where P
j
is the pro-
jection matrix after the rotation. The first image can
be represented by I(x
i
,y
i
), where (x
i
,y
i
) is the inho-
mogeneous coordinates of the image point. Similarly
the second image can be represented by J(x
j
,y
j
). Let
the surface of the object be represented by Z(X,Y).
Suppose that the camera is set on the negative Z-
axis. The unit normal of the surface is denoted by
n(X,Y) =
(Z
X
,Z
Y
,−1)
⊤
√
Z
X
2
+Z
Y
2
+1
,where Z
X
=
∂Z
∂X
and Z
Y
=
∂Z
∂Y
.
After rotating the object by a small angle θ around the
Y-axis, the normal of the surface point becomes
n
θ
(X,Y) =
cosθ 0 sinθ
0 1 0
−sinθ 0 cosθ
Z
X
Z
Y
−1
=
Z
X
cosθ−sinθ
Z
Y
−Z
X
sinθ−cosθ
.
(1)
Directional light is considered in this paper and it is
expressed as a vector l = (l
1
,l
2
,l
3
)
⊤
. Since the object
is considered to have a lambertian surface, the inten-
sities of the surface point in the two images are given
by
I(x
i
,y
i
) = ρl
⊤
n =
ρ(l
1
Z
X
+ l
2
Z
Y
−l
3
)
p
Z
X
2
+ Z
Y
2
+ 1
, (2)
J(x
j
,y
j
) = ρl
⊤
n
θ
=
ρ((l
1
cosθ−l
3
sinθ)Z
X
+ l
2
Z
Y
−l
1
sinθ−l
3
cosθ))
p
Z
X
2
+ Z
Y
2
+ 1
. (3)
where ρ is the albedo for the current point. If θ is
very small, (3) can be approximated by
J(x
j
,y
j
) ≈
ρ((l
1
−l
3
θ)Z
X
+ l
2
Z
Y
−l
1
θ−l
3
))
p
Z
X
2
+ Z
Y
2
+ 1
. (4)
The albedo and the normal term (denominator) can be
eliminated by subtracting (2) from (4), and dividing
the result by (2). This gives
(l
1
Z
X
+ l
2
Z
Y
−l
3
)(J(x
j
,y
j
) −I(x
i
,y
i
))
= (−l
1
θ−l
3
Z
X
θ)I(x
i
,y
i
).
(5)
Note that some points may become invisible after ro-
tation and that the correspondences between image
SHAPE FROM SHADINGS UNDER PERSPECTIVE PROJECTION AND TURNTABLE MOTION
29
points are unknown beforehand. If the object has a
smooth surface, the intensity of the 3D point in the
second image can be approximated by its intensity in
the first image through the first-order 2D Taylor series
expansion:
J(x
j
,y
j
) ≈ J(x
i
,y
i
) + J
x
(x
i
,y
i
)(x
j
−x
i
) + J
y
(x
i
,y
i
)(y
j
−y
i
).
(6)
Therefore,
J(x
j
,y
j
) −I(x
i
,y
i
) ≈ J(x
i
,y
i
) −I(x
i
,y
i
)+
J
x
(x
i
,y
i
)(x
j
−x
i
) + J
y
(x
i
,y
i
)(y
j
−y
i
).
(7)
Substituting (7) into (5) gives
(l
1
V
JI
+ l
3
I(x
i
,y
i
)θ)Z
X
+ l
2
V
JI
Z
Y
= −l
1
θI(x
i
,y
i
) (8)
where
V
JI
= J(x
i
,y
i
) −I(x
i
,y
i
) + J
x
(x
i
,y
i
)(x
j
−x
i
)
+J
y
(x
i
,y
i
)(y
j
−y
i
).
Note that x
i
, y
i
, x
j
, and y
j
are functions of X, Y, and
Z, and (8) can be written more succinctly as
a(X,Y,Z)Z
X
+ b(X,Y, Z)Z
Y
= c(X,Y,Z) (9)
where
a(X,Y,Z) = l
1
V
JI
+ l
3
I(x
i
,y
i
)θ,
b(X,Y,Z) = l
2
V
JI
,
c(X,Y,Z) = −l
1
θI(x
i
,y
i
). (10)
(9) is a first-order partial differential equation in
Z(X,Y). Furthermore, it is a qusi-linear partial differ-
ential equation since it is linear in the derivatives of
Z, and its coefficients, namely a(X,Y,Z), b(X,Y,Z),
and c(X,Y,Z), depend on Z. Therefore, the shape of
the object can be recovered by solving this first or-
der quasi-linear partial differential equation using the
method of characteristics. The characteristic curves
can be obtained by solving the following three ordi-
nary differential equations:
dX(s)
ds
= a(X(s),Y(s),Z(s)),
dY(s)
ds
= b(X(s),Y(s),Z(s)),
dZ(s)
ds
= c(X(s),Y(s),Z(s)), (11)
where s is a parameter for the parameterization of
the characteristic curves. (Basri and Frolova, 2008)
has given a detailed explanation of how the method
of characteristics works. It is also noticed that the
quasi-linear partial differential equation should have
a unique solution. Otherwise, the recovered surface
may not be unique. In the literature of quasi-linear
partial differential equation, this is considered as the
initial problem for quasi-linear first order equations.
A theorem in (Zachmanoglou and Thoe, 1987) can
guarantee that the solution is unique in the neighbor-
hood of the initial boundary curve. However, the size
of the neighborhood of the initial point is not con-
strained. It mainly depends on the differential equa-
tion and the initial curve. It is very important to find
an appropriate Dirichlet boundary. In this paper, dy-
namic programming is used to derive the boundary
curve.
3 BOUNDARY CONDITION
Under perspective projection, the Dirichlet Boundary
condition cannot be obtained in the same way as in
(Basri and Frolova, 2008). As noted in (Basri and
Frolova, 2008), the intensities of the contour genera-
tor points are unaccessible. Visible points (X
′
,Y
′
,Z
′
)
nearest to the contour generator are a good choice for
boundary condition. If the normal n
′
of (X
′
,Y
′
,Z
′
)
is known, Z
X
and Z
Y
can be derived according to
n(X,Y) =
(Z
X
,Z
Y
,−1)
⊤
√
Z
X
2
+Z
Y
2
+1
. Note that (9) also holds for
(X
′
,Y
′
,Z
′
). Therefore, (X
′
,Y
′
,Z
′
) can be obtained by
solving (9) with known Z
X
and Z
Y
values. The prob-
lem of obtaining (X
′
,Y
′
,Z
′
) becomes the problem of
how to obtain n
′
.
Let (X,Y,Z) be a point on the contour generator
(see Figure 1). Since (X,Y,Z) is a contour genera-
tor point, its normal n
c
must be orthogonal to its vi-
sual ray V. Consider a curve C given by the inter-
section of the object surface with the plane π defined
by V and n
c
. In a close neighborhood of (X,Y,Z),
the angle between V and the surface normal along C
would change from just smaller than 90 degrees to
just greater than 90 degrees. Now consider a visible
point (X
′
,Y
′
,Z
′
) on C close to (X,Y,Z), its normal
n
′
should make an angle of just smaller than 90 de-
grees with V. If (X
′
,Y
′
,Z
′
) is very close to (X,Y, Z),
n
′
would also be very close to n
c
. To simplify the es-
timation of n
′
, it is assumed that n
′
is coplanar with
n
c
and lying on π. n
′
can therefore be obtained by
rotating n
c
around an axis given by the normal N of π
by an arbitrary angle γ. According to the lambertian
law, n
′
can be obtained by knowing the intensities of
corresponding points across different views and the
albedo. However, no prior knowledge of point cor-
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
30

respondences and albedo ρ are available. Similar to
the solution in (Basri and Frolova, 2008), ρ and γ can
be obtained alternatively. The image coordinates of
the visible point nearest to the contour generator can
be obtained by searching along a line ℓ determined by
the intersection of the image plane o and π. As for
each γ in the range 0 < γ ≤
π
6
, a corresponding albedo
is computed and ρ is chosen as the mean of these
computed values. γ is then computed by minimizing
(I −ρl
⊤
R(γ)n
c
)
2
, where R(γ) is the rotation matrix
defined by the rotation axis ℓ and rotation angle γ. n
′
is finally determined as R(γ)n
c
and (X
′
,Y
′
,Z
′
) can be
obtained by minimizing
E
bon
= ka(X
′
,Y
′
,Z
′
)Z
X
+ b(X
′
,Y
′
,Z
′
)Z
Y
−c(X
′
,Y
′
,Z
′
)k
2
.
(12)
Dynamic programming is used to obtain (X
′
,Y
′
,Z
′
).
Two more constraints are applied in the framework
of dynamic programming. One is called photometric
consistency which is defined as
E
pho
(p) =
∑
q
(I
q
(p) −l
⊤
n
q
(p))
2
, (13)
where p is a 3D point on the contour generator, and
I
q
(p) is a component of the normalized intensity mea-
surement vector which is composed of the measure-
ment of intensities in q neighboring views and n
q
(p)
is the normal of p in the q
th
neighboring view.
The other constraint is called surface smoothness
constraint which is defined as:
E
con
(p, p
′
) = kpos(p) − pos(p
′
)k
2
2
(14)
where pos(p) denotes the 3D coordinates of point p
and pos(p
′
) denotes the 3D coordinates of its neigh-
bor point p
′
along the boundary curve.
The final Energy function is defined as
E = µE
bon
+ ηE
pho
+ ωE
con
(15)
where µ, η, ω are weighting parameters. By mini-
mizing (15) for each visible point nearest to the con-
tour generator, the nearest visible boundary curve can
be obtained and used as Dirichlet Boundary condition
for solving (9).
4 EXPERIMENTS
The proposed method is tested on synthetic models
and real image sequence. The camera and light source
are fixed and fully calibrated. Circular motion se-
quences are captured either through simulation or by
rotating the object on a turntable for all experiments.
Since the derivedfirst order quasi-linear partial differ-
ential equation is based on the assumption of small ro-
tation angle, the image sequences are taken at a spac-
ing of at most five degrees.
Figure 1: Computing boundary condition. The visible curve
nearest to contour generator is a good choice for the bound-
ary condition. The curve can be obtained by searching the
points whose normal is coplanar with those of the respective
contour generator points.
Figure 2: Shadow effect for shape recovery. Left column:
original image for one view used for shape recovery and
shadow appears near the left arm of the Venus model. Mid-
dle column: characteristic curves without using intensity
difference threshold for the solution of partial differential
equation. Right column: characteristic curves after using
intensity difference threshold for the solution of partial dif-
ferential equation.
It has been assumed that the synthetic model has a
pure lambertian surface since the algorithm is derived
according to the lambertian surface property. It is also
quite important to get good boundary conditions for
solving the partial differential equations.
As for synthetic experiment, it is easier to gen-
erate the image without specularities. However, it is
hard to control the image sequence without shadows
due to the lighting directions and the geometry of the
object. From (9), (10), and (11), it can be noted that
the solution of the first order quasi-linear partial dif-
ferential equation mainly depends on the change of
the intensities in the two images. If the projection of
the point in the first view is in shadow, the estima-
SHAPE FROM SHADINGS UNDER PERSPECTIVE PROJECTION AND TURNTABLE MOTION
31
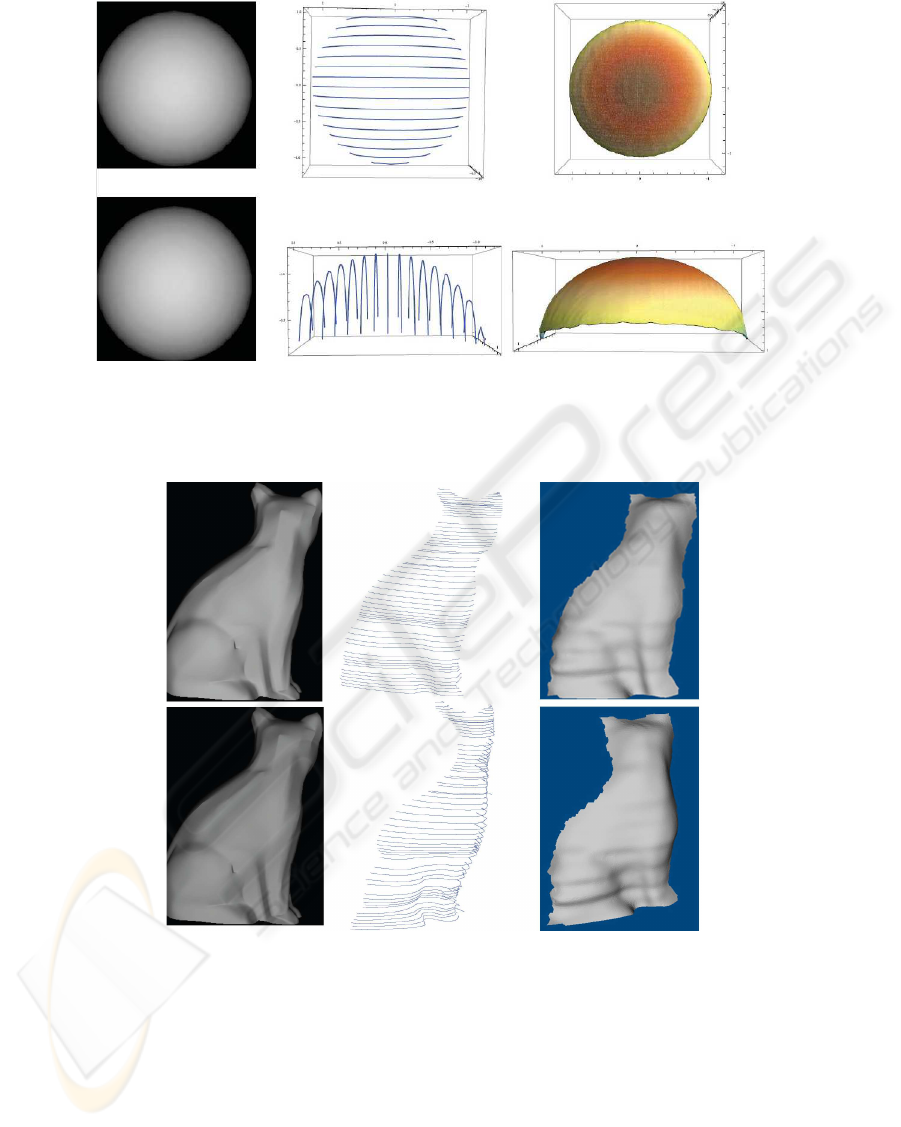
Figure 3: Reconstruction of the synthetic sphere model with uniform albedo. The rotation angle is 5 degrees. Light direction
is [0, 0, −1]
⊤
, namely spot light. Camera is set on the negative Z-axis. Left column: two original images. Middle column:
characteristic curves for frontal view (top) and the characteristic curves observed in a different view (bottom). Right column:
reconstructed surface for front view (top) and the reconstructed surface in a different view (bottom).
Figure 4: Shape recovery for the synthetic cat model. Left column: two images used for reconstruction. Middle column:
characteristic curves for the view corresponding to the top image in the left column (top) and the characteristic curves observed
in a different view (bottom).Right column: Recovered shape with shadings in two different views.
tion of the image intensity using Taylor expansion in
the second view will also be inaccurate. The charac-
teristic curves will go crazy (see Figure 2). In order
to avoid the great error caused by shadow effect, the
intensity difference for the estimation points should
not be larger than a threshold δ
thre
which is obtained
through the experiments.
4.1 Experiment with Synthetic Model
The derived first order quasi-linear partial differential
equation is applied to three models, namely the sphere
model, cat model, and Venus model. δ
thre
= 51 is used
for all the synthetic experiments to avoid the influence
of shadow in the image.
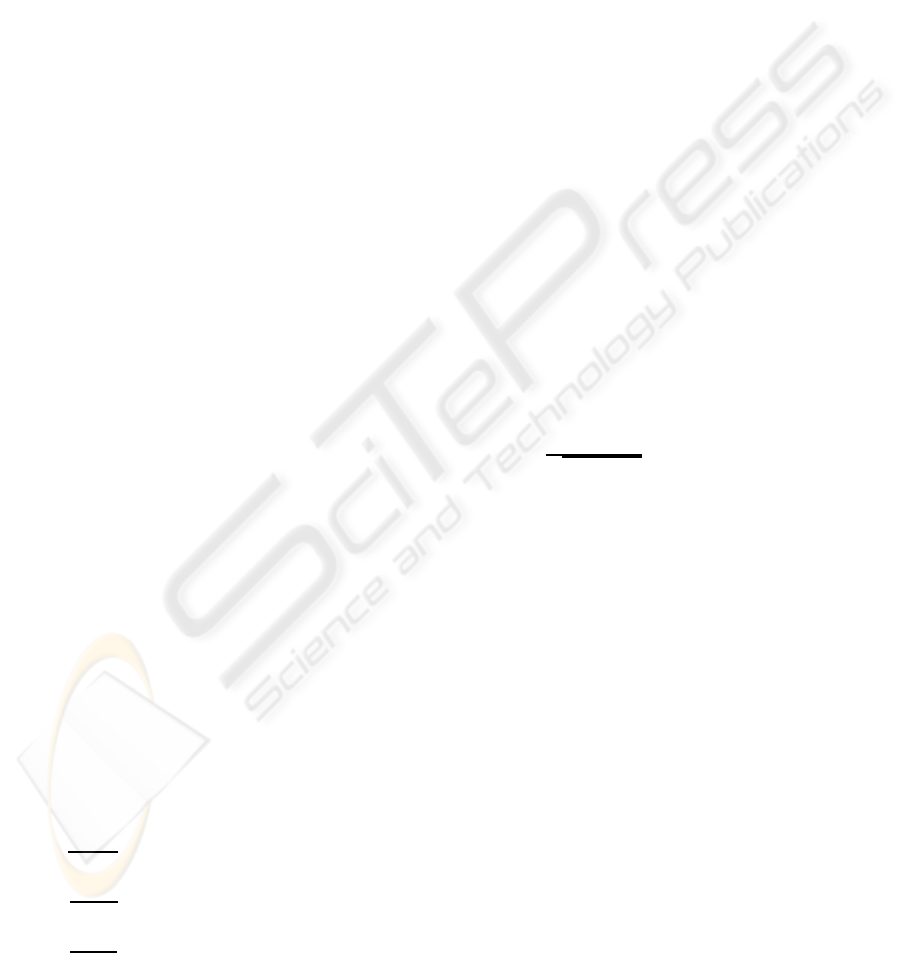
The first simulation is implemented on the sphere
model. Since the image of the sphere with uniform
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
32
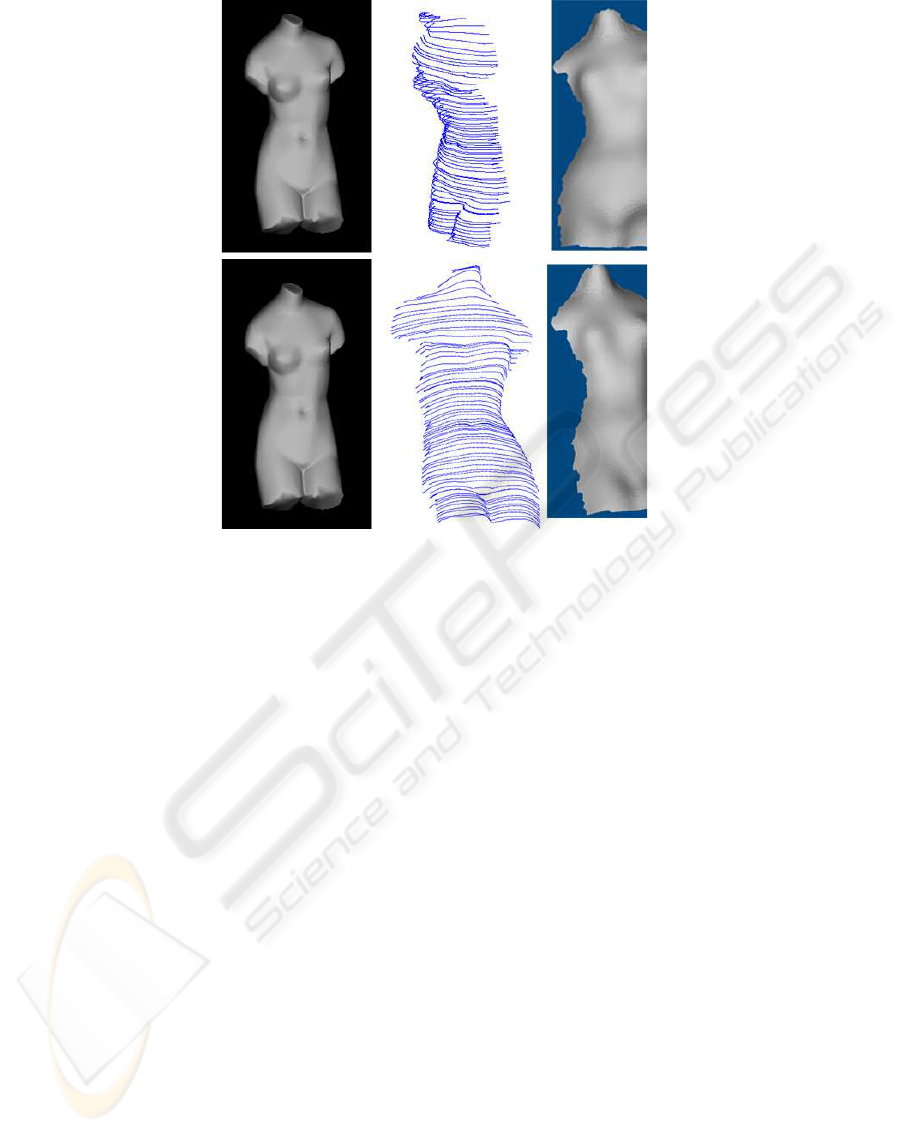
Figure 5: Shape recovery for the Venus model. Left column: two images used for shape recovery. Middle column: charac-
teristic curves for the view corresponding to the top image in the left column (top) and the characteristic curves observed in a
different view (bottom).Right column: Recovered shape with shadings in two different views.
albedo does not change its appearance after its ro-
tation around Y-axis (see Figure 3), only one image
is used to recover the 3D shape. Any small angle can
be used to the proposed equation. Nonetheless, if the
sphere has non-uniform albedo, two images will be
used for shape recovery. Figure 3 shows the original
images, the characteristic curves observed in two dif-
ferent views, and the recovered 3D shape examined
in two different views. The sphere model is assumed
to have a constant albedo. The reconstruction error is
tested by using k
ˆ
Z −Zk
2
2
/kZk
2
2
, where
ˆ
Z denotes the
estimated depth for each surface point and k·k
2
de-
notes the l
2
norm. The mean error is 4.63% for the
sphere with constant albedo which is competitive to
the result in (Basri and Frolova, 2008).
The second simulation is implemented on a cat
model. The image sequence is captured under gen-
eral lighting direction and with rotation angles at three
degrees spacing. Seven images are used to get the
boundary condition. Two neighboring images are
used for solving the derived quasi-linear partial dif-
ferential equation. The results are shown in Figure 4.
It can be observed that the body of the cat can be re-
covered except a few errors appeared at the edge. The
last simulation is implemented on a Venus model. The
sequence is taken at a spacing of five degrees.
Similarly seven images are used for getting the
boundary condition.
The front of the Venus model is recovered by us-
ing two neighboring view images for solving the de-
rived quasi-linear partial differential equation. The re-
sult is shown in Figure 5.
After the recovery of characteristics curves,
shapes for the Cat and Venus model with shadings are
shown by using the existing points to mesh software
VRmesh. The right columns of Figure 4, and Figure
5 show the results.
4.2 Experiment with Real Images
The real experimentis conducted on a ceramic mouse.
The mouse toy is put on a turntable. The relative po-
sitions of the lighting and the camera is fixed. The
image sequence is taken by a Cannon 450D camera
with a 34 mm lens. The camera is calibrated using
a chessboard pattern and a mirror sphere is used to
calibrate the light. The image sequence is captured
with the rotation angle at five degree spacing. It can
be observed that there are specularities on the body of
the mouse. The intensity threshold is used to elimi-
nate the bad effect of the specularities since the pro-
posed algorithm only works well on lambertian sur-
SHAPE FROM SHADINGS UNDER PERSPECTIVE PROJECTION AND TURNTABLE MOTION
33
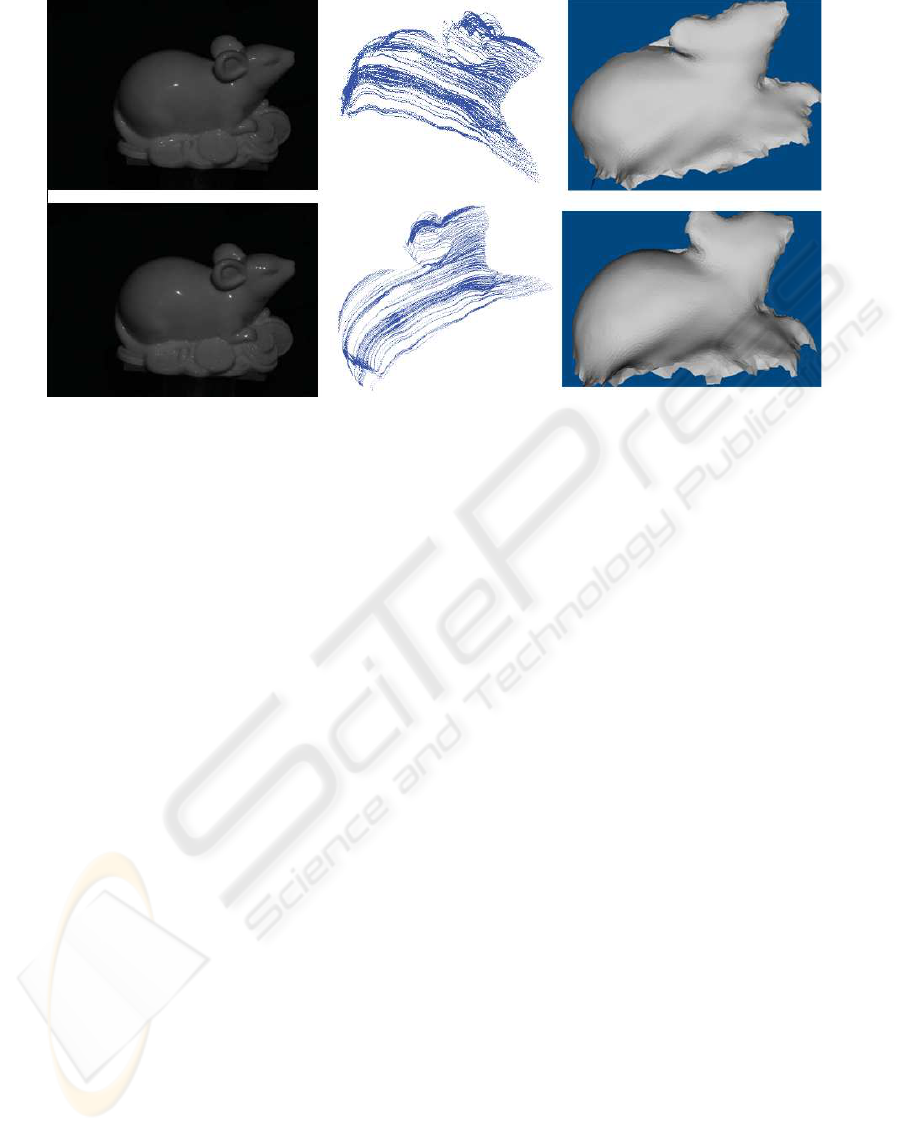
Figure 6: Shape recovery for a mouse toy. Left column: two images used for shape recovery. Middle column: characteristic
curves for the view corresponding to the top image in the left column (top) and the characteristic curves observed in a different
view (bottom).Right column: Recovered shape with shadings in two different views.
face. In order to avoid the shadow effect for solv-
ing the partial differential equation, δ
thre
= 27 is used
which is smaller than the value used in the synthetic
experiment since the captured images are compara-
tively darker. The original images and the charac-
teristic curves are shown in Figure 6. Although the
mouse toy has a complex topology and the images
have shadows and specularities, good results can be
obtained under this simple setting. Right column of
Figure 6 shows the results.
5 CONCLUSIONS
This paper re-examines the fundamental ideas of the
Two-Frame-Theory and derives a different form of
first order quasi-linear partial differential equation for
turntable motion. It extends the Two-Frame-Theory
to perspective projection, and derives the Dirich-
let boundary condition using dynamic programming.
The shape of the object can be recovered by the
method of characteristics. Turntable motion is con-
sidered in the paper as it is the most common setup
for acquiring images around an object. Turntable mo-
tion also simplifies the analysis and avoids the dif-
ficulty of obtaining the rotation angle in (Basri and
Frolova, 2008). The newly proposed partial differen-
tial equation makes the two frame method more use-
ful for a more general setting. Although the proposed
method is promising, it still has some limitations. For
instance, the proposed algorithm cannot deal with ob-
ject rotating with large angles. If the object rotates
with large angle, image intensities on the second im-
age cannot be approximated by the two dimensional
Taylor expansion. Some coarse-to-fine strategies can
be used to derive new equations. In additions, the ob-
ject is assumed to have a lambertian surface and the
lighting is assumed to be a directional light source.
The recovered surface can be used as an initialization
for shape recovery method using optimization, which
can finally get a full 3D model. Further improvement
should be made before the method can be applied to
an object under general lightings and general motion.
REFERENCES
Basri, R. and Frolova, D. (2008). A two-frame theory of
motion, lighting and shape. In 2008 IEEE Computer
Society Conference on Computer Vision and Pattern
Recognition, 24-26 June 2008, Anchorage, Alaska,
USA, pages 1–7. IEEE Computer Society.
Jin, H., Cremers, D., Wang, D., Prados, E., Yezzi, A. J., and
Soatto, S. (2008). 3-d reconstruction of shaded objects
from multiple images under unknown illumination.
International Journal of Computer Vision, 76(3):245–
256.
Liang, C. and Wong, K.-Y. K. (2005). Complex 3d shape
recovery using a dual-space approach. In 2005 IEEE
Computer Society Conference on Computer Vision
and Pattern Recognition, 20-26 June 2005, San Diego,
CA, USA, pages 878–884.
Moses, Y. and Shimshoni, I. (2006). 3d shape recov-
ery of smooth surfaces: Dropping the fixed view-
point assumption. In Computer Vision - ACCV 2006,
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
34

7th Asian Conference on Computer Vision, Hyder-
abad, India, January 13-16, 2006, Proceedings, Part
I, volume 3851 of Lecture Notes in Computer Science,
pages 429–438. Springer.
Pollefeys, M., Vergauwen, M., Verbiest, F., Cornelis, K.,
and Gool, L. V. (Jun. 2001). From image sequences
to 3d models. In In Proceedings 3rd international
workshop on automatic extraction of man-made ob-
jects from aerial and space images, pages 403–410.
Tankus, A. and Kiryati, N. (2005). Photometric stereo
under perspective projection. In 10th IEEE Interna-
tional Conference on Computer Vision , 17-20 Octo-
ber 2005, Beijing, China, pages 611–616.
Tomasi, C. (1992). Shape and motion from image streams
under orthography: a factorization method. Interna-
tional Journal of Computer Vision, 9:137–154.
Wong, K.-Y. K. and Cipolla, R. (2001). Structure and mo-
tion from silhouettes. In 8th International Confer-
ence on Computer Vision,July 7-14, 2001, Vancouver,
British Columbia, Canada, pages 217–222.
Woodham, R. (Jan. 1980). Photometric method for deter-
mining surface orientation from multiple images. In
OptEng 19(1), pages 19(1):139–144.
Zachmanoglou, E. C. and Thoe, D. W. (1987). Introduc-
tion to partial differential equations with applications.
Dover Publications, New York:SUS.
Zhang, L., Curless, B., Hertzmann, A., and Seitz, S. M.
(2003). Shape and motion under varying illumina-
tion: Unifying structure from motion, photometric
stereo, and multi-view stereo. In 9th IEEE Interna-
tional Conference on Computer Vision, 14-17 October
2003, Nice, France, pages 618–625.
SHAPE FROM SHADINGS UNDER PERSPECTIVE PROJECTION AND TURNTABLE MOTION
35
