AN EMPIRICAL EVALUATION OF A GPU RADIOSITY SOLVER

Guenter Wallner

Institute for Art and Technology, University of Applied Arts, Oskar Kokoschka Platz 2, Vienna, Austria

Keywords:

Global illumination, Radiosity, GPU programming, Projections.

Abstract:

This paper presents an empirical evaluation of a GPU radiosity solver which was described in the authors pre-

vious work. The implementation is evaluated in regard to rendering times in comparision with a classical CPU

implementation. Results show that the GPU implementation outperforms the CPU algorithm in most cases,

most importantly, in cases where the number of radiosity elements is high. Furthermore, the impact of the

projection – which is used for determining the visibility – on the quality of the rendering is assessed. Results

gained with a hemispherical projection performed in a vertex shader and with a real non-linear hemispherical

projection are compared against the results of the hemicube method. Based on the results of the evaluation,

possible improvements for further research are pointed out.

1 INTRODUCTION

Radiosity has been and is still a widely used tech-

nique to simulate diffuse interreﬂections in three-

dimensional scenes. Radiosity methods were ﬁrst de-

veloped in the ﬁeld of heat transfer and in 1984 gener-

alized for computer graphics by (Goral et al., 1984).

Since then, many variations of the original formula-

tion have been proposed, leading to a rich body of

literature available on this topic. See e.g. the book by

(Cohen and Wallace, 1995) for a good overview of the

ﬁeld. An extensive comparison of different radiosity

algorithms can be found in (Willmott and Heckbert,

1997).

In recent years research on GPU accelerated ra-

diosity algorithms intensiﬁed. (Nielsen and Chris-

tensen, 2002) used hardware texture mapping to ac-

celerate the hemicube method and (Carr et al., 2003)

were the ﬁrst to utilize ﬂoating point textures to store

the radiosity values. (Coombe et al., 2003; Coombe

and Harris, 2005) described the ﬁrst radiosity solver

for planar quadrilaterals that performed all steps on

programmable graphics hardware. In (Wallner, 2008)

we described a GPU radiosity system for arbitrary tri-

angular meshes which built upon the work mentioned

above.

The purpose of this paper is twofold. First, pre-

senting the results of an empirical evaluation of our

GPU radiosity solver in regard to rendering times and

on how the projection used for creating the visibility

map effects the ﬁnal image quality and secondly to

point out possible improvements for further develop-

ment.

The reminder of this paper is structuredas follows.

Section 2 gives a short overview of the various steps

of the radiosity implementation. In Section 3 timings

for the individual steps are given for a set of sample

scenes. Section 4 compares rendering times with a

CPU implementation and the impact of the applied

projection on the quality of the result is discussed in

Section 5. The paper is concluded in Section 6.

2 OVERVIEW

This section gives a short overview of the main steps

performed by the progressive radiosity solver, which

are as follows:

Preprocess. In the preprocess two textures – which

store radiosity and residual energy values – are gener-

ated for each triangle which themselves are placed in

larger lightmaps to reduce texture switching later in

the process. Furthermore the required framebuffers,

auxiliary textures and other OpenGL related resources

are allocated.

Next Shooter Selection. In this step a mipmap pyra-

mid is constructed for each residual lightmap until

each triangle is represented by a single texel. These

values are read back to the CPU and the triangle with

the highest value is selected as next shooter. This step

is performed using a ping-pong technique. Standard

225

Wallner G. (2010).

AN EMPIRICAL EVALUATION OF A GPU RADIOSITY SOLVER.

In Proceedings of the International Conference on Computer Graphics Theory and Applications, pages 225-232

DOI: 10.5220/0002822202250232

 SciTePress

OpenGL mipmapping cannot be used because texels

not occupied by the triangle have to be omitted. For

the shooter, four textures – world position map, nor-

mal map, color map and intensity map – are gener-

ated which are necessary for calculation of the energy

transport. Shooting is performed from a user-deﬁned

mipmap level of these textures. This way the accuracy

and speed of the calculation can be inﬂuenced.

Render Visibility Texture. To determine the visible

surfaces a hemicube projection, a stereographic pro-

jection (performed in the vertex shader) or the non-

linear hemisphere projection by Gascuel et al. (Gas-

cuel et al., 2008) is used to generate a depth texture

from the shooter’s viewpoint.

Adaptive Subdivision. If adaptive subdivision is en-

abled, occlusion queries are used during rendering

of the visibility texture, to check on which triangles

shadow boundaries are located. If the ratio between

visible texels and texels in shadow is between certain

thresholds and the maximum subdivision level is not

reached, the triangle is subdivided.

Update Receivers. Visible or partially visible trian-

gles (determined by checking the outcome of an oc-

clusion query) are back-projected into the visibility

texture and their depth values are compared against

the stored values. If they match, then the radiosity

and residual maps are updated accordingly. Calcula-

tion of the form factors is therefore performed in this

step.

Postprocess. Because the rasterized triangles cannot

be directly used for texturing – polygon rasterization

rules differ from texture sampling rules (Segal and

Akeley, 2003) – missing values are linearly interpo-

lated in a shader. This step is performed once after

the progressive radiosity solver has ﬁnished.

The system was implemented in C++ and OpenGL

with the shaders written in Cg. For a more in-depth

description of the solver refer to (Wallner, 2008) and

(Wallner, 2009). In the remainder of this paper we

will refer to one cycle of the progressive radiosity

solver as an iteration in contrast to a shooting step

from a single texel of the mipmap texture of the se-

lected shooting triangle.

3 PERFORMANCE

To assess the time spent on the above mentioned steps

we used four different test scenes, which vary in the

number of triangles and light sources. All the mea-

surements in this work were taken on an Intel Core2

CPU with 2.13 GHz, 3.5 GB RAM with a Geforce

Figure 1: Time spent on different steps of the radiosity com-

putation for different scenes with increasing triangle count

from left to right (each time for three different resolutions

as listed in Table 1) for 32 shootings. The left group shows

steps executed once, whereas the steps in the right side are

performed multiple times.

8800GTS with 640MB DDR3 Ram. The scenes (ex-

cept the Cornell Box) are shown in Figure 2 whereas

Figure 1 depicts the measurements in case of the non-

linear hemisphere. The hemicube is rendered with a

single-pass cubemap geometry shader with multiple

attached layers. This has the advantage that an oc-

clusion query (required for subdivision and visibility

purposes) counts all rasterized fragments over all at-

tached layers, which makes management of them eas-

ier than with a multi-pass approach. Performing the

hemispherical projection in the vertex shader reduces

the time needed for the creation of the visibility tex-

ture by about 30 to 55 percent. However, if the scene

is not carefully triangulated the hemispherical projec-

tion can lead to severe artifacts (see Section 5).

Time for rendering the visibility texture depends

solely on the number of triangles, whereas the time

needed for the next shooter selection depends on the

number of lightmaps and the ratio of the lightmap size

to the stored texture size. Updating the receivers is

by far the most time consuming function in the pro-

cess. In this regard the biggest restriction is currently

that GPUs do not allow to simultaneously read from

and write to the same position in a texture. There-

fore it is necessary to render the new radiosity and

residual maps to intermediate textures and copy them

afterward to the correct position in the lightmap. An-

other possibility would be to maintain two textures

for storing the radiosity and further two for the resid-

ual energy and use them in a ping pong technique.

We rejected this method because it would double the

memory requirements.

The cost for the post-process primarily depends on

the number of triangles. To reduce the required time

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

226

Figure 2: These are the different test scenes used for the analysis. From left to right: A temple with three light sources (6

triangles), an old ofﬁce with 24 light emitting triangles distributed over four light sources and a more modern room with one

light source (2 triangles).

for the post-process we initially hoped that with con-

servative rasterization (Hasselgren et al., 2005) the

textures could be directly used for nearest-neighbor

texture sampling. This, however, proved to be difﬁ-

cult since the geometry itself is inﬂated and therefore

the interpolation of normals and other attributes is al-

tered, which inevitable leads to discontinuities at the

boundaries of the triangles. It is clear that the cost of

the pre- and post-process amortizes with increasing

number of performed iterations.

4 CPU COMPARISON

To compare the performance of our solution with

a software implementation we chose the radiosity

solver of the open source software Blender 2.48a

(Blender Foundation, b). We opted for Blender be-

cause it is freely available and the settings of its ra-

diosity system can be closely matched with the ones

from our implementation. The hemicube resolution

was set to 512× 512 and in case of the stereographic

projection a 2048 × 2048 resolution was used. The

calculation was terminated after a ﬁx number of iter-

ations. We have preferred iterations over convergence

because the time needed to reach a certain conver-

gence depends on the mipmap level chosen for shoot-

ing in our method. Ensuring the same number of it-

erations between the CPU and GPU implementation

would therefore be hard to control. Adaptive sub-

division was disabled in our implementation, since

Blender performs no adaptive reﬁnement (Blender

Foundation, a). Table 1 lists the timings for differ-

ent scenes. For the test scenes our GPU implemen-

tation achieved speed-ups of up to 46 times. In con-

trast to the CPU implementation, the calculation time

is nearly unaffected by the number of elements (that

is, the resolution of the radiosity maps). Calculation

time on the GPU is mostly determined by the num-

ber of triangles in the scene, since for each triangle a

texture copy is performed during update of the radios-

ity and residual textures. The non-linear hemisphere

projection achieved about 20 to 40 percent faster ren-

dering times than the hemicube method.

In cases where the number of elements is very low

the CPU outperforms the GPU, as it is e.g. the case

in the low resolution temple scene. In such scenarios

the cost of the initial pre-process of transferring the

data to the GPU, the allocation of resources and the

required post-process are high compared to the actual

processing time.

5 PROJECTIONS

In this section the inﬂuence of the projection utilized

for creating the visibility map on the visual quality of

the result is discussed. The classical method for deter-

mining visibility from a given point is the hemicube,

as proposed by (Cohen and Greenberg, 1985). The

drawback is that the scene has to be rendering ﬁve

times to project all possible receiving surfaces onto

the individual sides of the hemicube. Since visibility

determination is a frequently performed task in the

radiosity process, it is beneﬁcial to reduce rendering

time. (Beran-Koehn and Pavicic, 1991; Beran-Koehn

and Pavicic, 1992) used a cubic tetrahedron instead a

hemicube, thereby reducing the number of projecting

planes to three. The number of projections were fur-

ther reduced by using a single-plane projection (e.g.

(Sillion and Puech, 1989)) or hemisphere (base) pro-

jections which, to our knowledge, were ﬁrst proposed

by (Spencer, 1992). In this case the projection is a

simple normalization process and clipping can sim-

ply be performed against the base plane of the hemi-

sphere. To ensure an accurate projection, (Spencer,

1992) calculates the degree of the arc between pairs of

points projected onto the hemisphere basis and uses

this value to calculate intermediate points along the

edge. A scan-conversion algorithm is then used to

AN EMPIRICAL EVALUATION OF A GPU RADIOSITY SOLVER

227

Table 1: Performance comparison between a CPU radiosity solver t

cpu

and our implementation (t

gpu,cube

for the hemicube

and t

gpu,sphere

for the non-linear hemispherical projection with the speed-up in brackets). The number of elements is given in

the columns n

cpu

and n

gpu

. Because our method uses power-of-two textures the number of elements differ, nonetheless we

tried to match them as closely as possible. n

lists the number of triangles and s the number of shootings.

Scene

s n

cpu

gpu

cpu

[s] t

gpu,sphere

[s] t

gpu,cube

[s]

cbox

low

32 258 9248 11802 1.97 0.79 (× 2.5) 1.15 (× 1.7)

cbox

medium

32 258 82976 94750 5.69 0.75 (× 7.6) 1.13 (× 5.0)

cbox

high

32 258 1026464 1115126 54.19 1.17 (× 46.3) 1.48 (× 36.6)

temple

low

24 15872 117248 126078 5.60 9.74 (× 0.6) 12.58 (× 0.4)

temple

medium

24 15872 507320 516312 18.27 9.92 (× 1.8) 12.72 (× 1.4)

temple

high

24 15872 1741208 2074242 53.13 10.03 (× 5.3) 13.18 (× 4.0)

ofﬁce

low

96 21704 264081 254572 36.17 18.46 (× 1.3) 42.46 (× 0.8)

ofﬁce

medium

96 21704 747375 854341 84.62 18.03 (× 4.7) 42.44 (× 2.0)

ofﬁce

high

96 21704 1846137 1843771 202.54 18.73 (× 10.8) 43.03 (× 4.7)

living

low

32 38147 474744 472317 37.23 20.18 (× 1.8) 33.10 (× 1.1)

living

medium

32 38147 861540 866330 44.41 20.05 (× 2.2) 33.24 (× 1.3)

living

high

32 38147 1570884 1612067 73.88 20.61 (× 3.6) 33.45 (× 2.2)

Figure 3: Left: Incorrect shadows as the result of erroneous visibility information due to the hemispherical projection. Mid-

dle: Adaptively tessellating the surface around the shadow boundary reduces the errors enormously. Right: Solution of the

hemicube method on the original mesh.

determine the area covered by the projected surface

element. The method, however, fails to remove hid-

den surfaces in certain cases, which was resolved by

(Doi and Takayuki, 1998) by subdividing the surface

– based on a solid angle criterion – into smaller trian-

gles instead of using edge-subdivision. Hemisphere

projections are currently frequently performed in ver-

tex shaders on programmable GPUs, e.g. (Coombe

et al., 2003; Barsi and Jakab, 2004; Coombe and Har-

ris, 2005). However, since only vertices are affected

by the hemispherical projection – straight edges are

mapped to straight edges instead of elliptical seg-

ments – errors are introduced. To approximate the

correct curvature, one solution would be to tessellate

the surfaces ﬁnely enough, as e.g. done in (Coombe

et al., 2003). This increases the triangle count of the

scene considerably and consequently rendering times.

Assuming that no two surfaces overlap, it is sufﬁcient

to perform the back-projection in the vertex shader

as done in (Wallner, 2008; Barsi and Jakab, 2004).

However, if surfaces overlap, the relative position in-

formation between the surfaces is distorted in the pro-

jection which results in more or less incorrect shadow

boundaries. Figure 3 illustrates this problem. How-

ever, adaptive subdivision methods (see e.g. (Cohen

and Wallace, 1995)) to improve the accuracy of the

radiosity solution in areas of high-frequency lighting

also reduce the errors due to the hemisphere projec-

tion signiﬁcantly. Therefore it seems to be unneces-

sary to uniformly tessellate the mesh just for the pur-

pose of the projection.

A further problem in conjunction with too coarse

meshes is that the projection of some triangles may

be extremely deformed and therefore are not rendered

at all, although they should be. These triangles are

misleadingly considered not visible and thus omitted

during the radiosity exchange. Figure 4 shows an ex-

ample where this is the case. This problem is intrin-

sic to hemispherical projections because distortions

increase for directions further from the viewing di-

rection. Using a paraboloid projection would reduce

these errors since the sampling rate is more uniform

than in the spherical case (see (Heidrich and Seidel,

1998)). However, the actual problem remains.

(Kautz et al., 2004) proposed a method for spher-

ical rasterization, by deﬁning a plane through each

edge of the triangle and the projection center. Then

a pixel is considered inside the projected image of the

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

228

Figure 4: Triangle D at the back wall is sometimes consid-

ered as not visible, since its projection is that much distorted

that it is not rendered during creation of the visibility tex-

ture (shown on the right side with a wireframe overlay to

better show the connection to the scene).

triangle if the corresponding point on the hemi-

sphere is above all three planes. Because they were

only concerned with low-resolution visibility masks,

they were able to precompute a lookup table of bit-

masks for a discrete set of planes. In our case this

method is not feasible because the visibility map is

too large. We therefore implemented the recently

published method by Gascuel et al. (Gascuel et al.,

2008) to calculate non-linear projections with a sin-

gle projection center on graphics hardware. Their

algorithm consists of two steps. First, a bounding

primitive for each triangle is computed in a geome-

try shader. Second, each fragment is tested whether it

is inside the original triangle or not (in which case the

fragment is discarded).

5.1 Quantitative Analysis

To quantitatively assess the errors introduced by the

hemispherical projection, different scenes were ren-

dered with this projection and with the hemicube

method. This was done three times for each scene,

once with the original geometry, once with adap-

tive subdivision and once with a regularly reﬁned

mesh. Each time the resulting lightmaps were read-

back from the GPU and compared with the root mean

square (RMS) metric. Calculating the RMS on the

lightmaps has the advantage that the estimated error

is view-independent. For N lightmaps of size X × Y

the RMS is given by

RMS =

∑

n=1

∑

x=1

∑

y=1

| · a

(1)

where v

is the color-difference vector between

the R, G, and B values at pixel position (x, y) between

the n-th lightmap produced by hemispheical projec-

tion and the corresponding lightmap computed with

the hemicube method.

Pixels which do not belong to a triangle in the

lightmap are neglected by multiplication with the the

alpha-value a

at the current position, which is either

1 or 0 if the pixel is occupied by a triangle or not.

This is necessary because such pixels are not part of

the solution and would only dilute the RMS value. m

is therefore the number of occupied pixels (a = 1) in

all lightmaps. Since the result of the adaptive subdivi-

sion can vary between the hemicube and hemisphere

solution, the result of the adaptive subdivision gained

by the hemisphere solution was used for the hemicube

method. Table 2 lists these root mean square values

for two different scenes. In this case we did not keep

the iterations ﬁxed but rather aborted the calculation

once a given convergence threshold was reached. The

measurements were performed for different subdivi-

sion levels with different texture sizes. For the origi-

nal mesh 256× 256 textures were used, which yields

a resolution of 512× 512 for a quad. This means the

regular subdivision with level 3 and a texture size of

64 matches the original resolution most closely.

First of all, the RMS-error in case of the Cornell

Box is higher throughout than for the column scene

since the light source is much closer to the scene ge-

ometry. As is apparent from Table 2 (and as expected)

a regular subdivision reduces the RMS error quite sig-

niﬁcantly, up to 13 times. This is the case even if

the overall resolution over a non-subdivided quad is

smaller than the 512× 512 texels used on the original

geometry (e.g. using a regular subdivision with level

3 and texture size 32 yields still a better result than

achieved with the original mesh). However, a regu-

larly subdivided mesh also increases rendering times

considerably. This is, on the one hand, due to the in-

creased number of triangles and, on the other hand –

which may not be obvious at ﬁrst – due to the fact

that more triangles covering the same area means less

energy per triangle which in turn requires more itera-

tions to reach a given convergence threshold.

We are looking into two options to further de-

crease rendering times:

1. Currently a single texture size is used for the

whole mesh (although sizes can vary between

meshes), which may be suboptimal since triangles

sizes can vary over the mesh. In this sense, it may

be promising to base the texture resolution on tri-

angle size. However, ﬁrst results showed inter-

polation artifacts along triangle edges due to the

different resolutions.

2. The mipmap level used for shooting may be de-

cided adaptively rather than being ﬁxed for the

whole calculation. The level may also depend

on the average energy of the current shooting tri-

AN EMPIRICAL EVALUATION OF A GPU RADIOSITY SOLVER

229

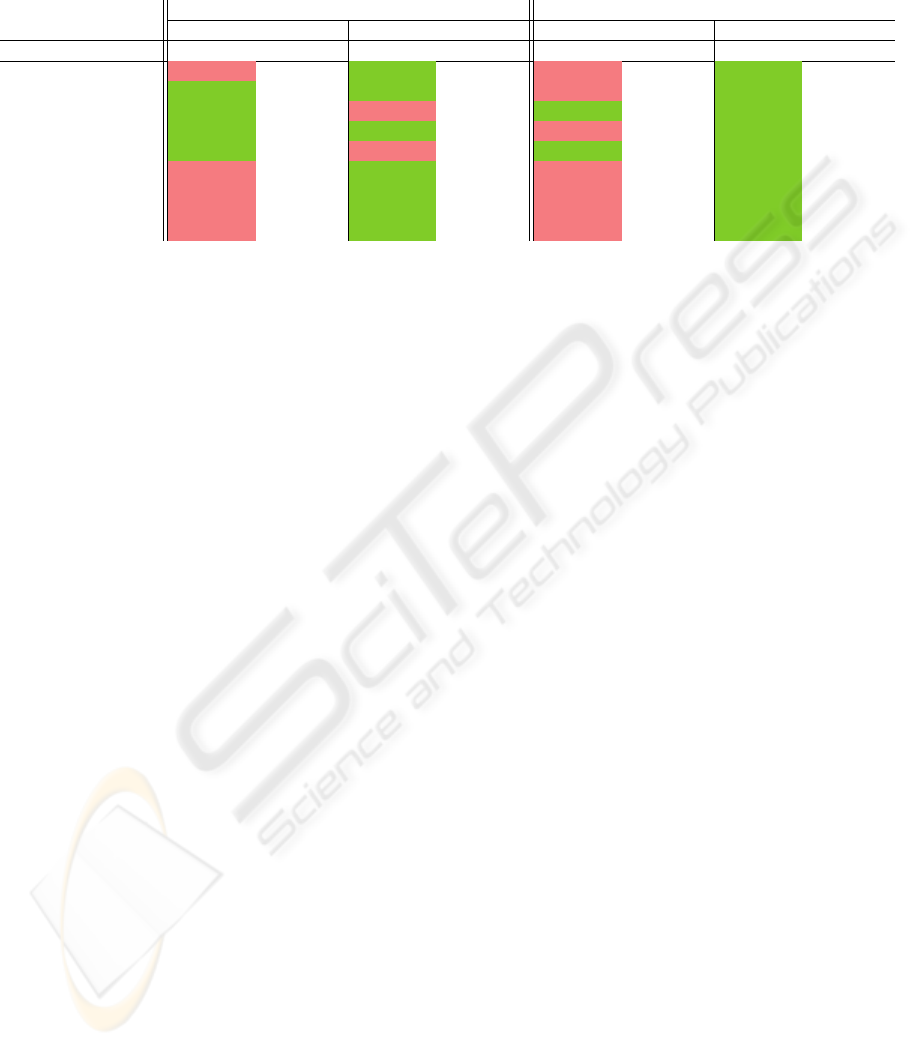
Table 2: RMS error for the hemispherical projection (compared to the hemicube solution). The table lists the type of subdi-

vision type

sub

which is either no (no subdivision), adapt (adaptive subdivision) or reg (regular reﬁnement), and the level of

subdivision. The texture size is given in column size and the rendering time is listed in column t. If a solution is considered

perceptually indistinguishable from the hemicube solution it is highlighted in green, otherwise in red.

Columns Cornell Box

hemisphere non-linear hemisphere hemisphere non-linear hemisphere

type

sub

level size RMS t[s] RMS t[s] RMS t[s] RMS t[s]

no 0 256 0.001745 1.836580 0.000279 2.191166 0.005399 1.543515 0.001286 2.265481

adapt 3 32

0.002047 0.997896 0.000953 2.134127 0.005451 3.731590 0.007660 4.174523

reg 3 32

0.000331 9.142668 0.000104 10.184814 0.001772 14.641043 0.000458 20.789242

adapt 3 64

0.000789 1.179061 0.000397 2.295658 0.002147 5.382289 0.002708 4.373851

reg 3 64

0.000133 28.540912 0.000057 29.953424 0.000766 79.602470 0.000237 97.384330

adapt 2 32

0.003907 0.903491 0.001434 1.968630 0.040701 1.466952 0.011807 3.244810

reg 2 32

0.001287 2.791759 0.000457 3.137670 0.004473 2.777053 0.001942 4.120059

adapt 2 64

0.001726 1.004140 0.000576 2.064948 0.020571 1.644687 0.004213 3.477550

reg 2 64

0.000591 3.272110 0.000187 3.731351 0.001784 4.809930 0.000709 7.562907

angle or on the global ambient radiosity term.

This would make sense, since triangles with less

residual energy make a smaller contribution to the

overall image. In the same way the most notice-

able contributions are being made at the beginning

of the progressive radiosity algorithm.

However, as evident from Table 2, the RMS error

can be already reduced by using adaptive subdivision

which simultaneously keeps rendering times low. In

fact, it reduces the most noticeable errors near shadow

boundaries as depicted in Figure 3. In some cases

rendering times are even lower than with the original

geometry. This is the case because lower resolutions

were used, meaning that there are less shootings from

a single triangle. In contrast to the regular subdivi-

sion, areas with no shadow boundaries (which there-

fore have higher residual energies on average) are not

reﬁned in the same extent which in turn means that the

energy is not distributed over that many triangles and

therefore the number of iterations is not increased by

the same extent as is the case for regular subdivision.

There is a special case in the results which may

need further explanation. In case of the three times

adaptively subdivided Cornell Box with a texture res-

olution of 64× 64, rendering with the hemispherical

projection is slower than with the non-linear hemi-

sphere projection. As described in Section 2 our sub-

division method is based on the ratio between visible

and occluded pixels of a triangle. This information

is gained from the visibility texture. In this partic-

ular example the visibility texture of the hemisphere

projection gives incorrect information about shadow

boundaries, yielding more subdivisions than actually

necessary. In contrast, the non-linear hemispherical

projection of Gascuel et al. (Gascuel et al., 2008)

gives much better RMS values. The remaining dif-

ferences are presumable caused by different resolu-

tions used for the hemicube and hemispherical visi-

bility maps and due to the increasing distortions to-

ward the perimeter. It should be pointed out that the

non-linear hemispherical projection may suffer from

the same sampling problems as the hemispherical pro-

jection: small triangles may be not visible in the pro-

jected image.

5.2 Perceptual Analysis

Although the RMS values quantitatively show the im-

provement in image quality, they do not reﬂect if the

improvement is sufﬁcient enough to avoid visual dif-

ferences noticeable by a human observer. Therefore

we used the perceptual metric of Yee (Yee, 2004)

to assess if there are perceptual differences between

the hemicube method and the hemispherical varia-

tions. We have chosen this method because an im-

plementation is publicly available. The algorithm re-

quires some user deﬁned parameters for which the

standard values were used, except for the ﬁeld-of-

view angle which was set to 37

◦

(assuming an ob-

server looking from 0.5m at a 17” display). An image

was considered different if more than 100 pixels (ap-

prox. 1.2% of the image) were perceptually different.

Since it does not make sense to apply the metric on

the lightmaps themselves, we rendered ﬁve different

views of each scene and applied the metric to the tone-

mapped result. Progressive radiosity was turned off

because it can change the shooting order and there-

fore can lead to slightly different results. A solution

was considered to have no difference only if all of the

views were indistinguishable.

The perceptual metric revealed two problems.

First, if silhouette edges are at glancing angles in re-

gard to the projection center, some texels around this

edge may be incorrectly classiﬁed as in-shadow if one

of the two hemispherical projections is used. This

seems to be caused by the discretized nature of the

visibility map in conjunction with limited depth pre-

cision. Sampling the visibility map at the neighboring

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

230

texels reduced these problems signiﬁcantly. Indistin-

guishable solutions after this modiﬁcation are high-

lighted green in Table 2, otherwise they have a red

background. The two red entries for the non-linear

hemispherical projection are caused by the formerly

described problem, that surfaces may not be visible

in the visibility map due to distortions. Second, if

a hemispherical projection is used, shadows may be

smaller or larger than they should be. This was ev-

ident in some results because it proved to be inade-

quate to subdivide only surface elements which are

partly in shadow as implemented in our adaption sub-

division algorithm. Rather is it necessary to subdi-

vide shadow casting surfaces as well, otherwise their

boundaries do not reproduce the circular arc accu-

rately enough (the surface being smaller or larger and

therefore allowing more respectively less light to im-

pinge on the receiving surfaces). An example where

this problem leads to larger shadows is shown in Fig-

ure 5. This issue may be resolved by adaptively tes-

sellating the triangles during creation of the visibility

map with a geometry shader. However, this subdivi-

sion also has to be considered during back-projection

of the individual surfaces. We will look into this issue

as part of our future work.

Finally, it should be pointed out that errors in the

visibility information may not only affect the image

quality of the solution but even the convergence of

the radiosity process. In some rare cases we even

observed longer rendering times with the hemisphere

projection as with the hemicube method, since many

areas are incorrectly considered to be in shadow

Figure 6 compares the convergence of a scene, where

the errors caused by the stereographic projection in-

creased the number of shootings from 3514 to 4106

and consequently the rendering time from 182.06 sec-

onds to 192.93 seconds.

6 CONCLUSIONS

In this paper we presented an analysis of our GPU

radiosity solver. Measurements showed that the per-

formance is mostly independent of the dimensions of

the radiosity maps (if the mipmap level for shooting

is adjusted accordingly to keep the number of shoot-

ings identical). The implementation would beneﬁt if

reading from and writing to the same texture location

were possible. In most cases the GPU implementa-

tion is considerably faster than the CPU implementa-

tion. The cost for setting up the required OpenGL re-

This mostly occurs near the perimeter of the hemi-

sphere where distortions are very common.

Figure 5: A typical problem caused by hemispherical pro-

jection. Although the shadow receiving surface (the wall) is

tessellated highly enough, the shadow caster (the picture) is

not. The bottom edge of the picture which is responsible for

the shadow is a straight line in the projection and therefore

leads to an elliptical shadow.

500

1000

1500

2000

2500

500

1000

1500

2000

2500

3000

3500

Residual Energy

Shootings

Living Room, Convergence

stereographic

hemicube

Figure 6: Comparison of the convergence for the ﬁrst 3500

shootings between hemisphere and hemicube projection.

Subdivision was disabled in both cases to highlight the ef-

fect of errors in the visibility information on the conver-

gence. Note the steep decrease near the beginning in the

case of the hemicube, which is not the case with the hemi-

spherical projection.

sources relativises with increasing number of radios-

ity elements and iterations.

Although a hemispherical projection performed in

the vertex shader accelerates the creation of the visi-

bility textures, it has several drawbacks which have an

impact on the quality of the result. First, the relative

position information of overlapping surfaces is dis-

torted, leading to incorrect shadow boundaries. Sec-

ond, extreme deformations may lead to incorrect vis-

ibility classiﬁcation, misleadingly considering com-

plete surfaces as not visible. Third, if the shadow

boundaries are incorrect due to erroneous visibility

information caused by the hemispherical projection,

AN EMPIRICAL EVALUATION OF A GPU RADIOSITY SOLVER

231

then the subdivision method may unnecessarily sub-

divide triangles which in turn leads to longer render-

ing times. A real non-linear projection overcomes

almost all of these drawbacks and at the same time

decreases rendering times considerably. However,

the non-linear projection still exhibits some distortion

and sampling problems which are intrinsic to hemi-

spherical projections. Finally, we proposed possible

solutions to problems which were revealed during the

evaluation and which will be part of our future work.

REFERENCES

Barsi, A. and Jakab, G. (2004). Stream processing in global

illumination. Proceedings of 8th Central European

Seminar on Computer Graphics.

Beran-Koehn, J. C. and Pavicic, M. J. (1991). A cubic tetra-

hedral adaptation of the hemicube algorithm. Graphic

Gems II, pages 299–302.

Beran-Koehn, J. C. and Pavicic, M. J. (1992). Delta form-

factor calculation for the cubic tetrahedral algorithm.

Graphics Gems III, pages 324–328.

Blender Foundation. Blender manual. available on-

line:

http://wiki.blender.org/index.php/Doc:

Manual

Blender Foundation. Blender product website.

http://

www.blender.org

Carr, N. A., Hall, J. D., and Hart, J. C. (2003). Gpu

algorithms for radiosity and subsurface scattering.

In HWWS ’03: Proceedings of the ACM SIG-

GRAPH/EUROGRAPHICS conference on Graphics

hardware, pages 51–59, Aire-la-Ville, Switzerland.

Eurographics Association.

Cohen, M. F. and Greenberg, D. P. (1985). The hemi-cube:

a radiosity solution for complex environments. In

SIGGRAPH ’85: Proceedings of the 12th annual con-

ference on Computer graphics and interactive tech-

niques, pages 31–40, New York, NY, USA. ACM

Press.

Cohen, M. F. and Wallace, J. R. (1995). Radiosity and Re-

alistic Image Synthesis. Morgan Kaufmann.

Coombe, G. and Harris, M. (2005). Global illumination

using progressive reﬁnement radiosity. In GPU Gems

2, pages 635–647. Addison-Wesley Professional.

Coombe, G., Harris, M., and Lastra, A. (2003). Radios-

ity on graphics hardware. Technical report, Univ. of

North Carolina, UNC TR03-020.

Doi, A. and Takayuki, I. (1998). Accelerating radiosity so-

lutions through the use of hemisphere-base formfactor

calculation. The Journal of Visualization and Com-

puter Animation, 9:3–15.

Gascuel, J.-D., Holzschuch, N., Fournier, G., and P

eroche,

B. (2008). Fast non-linear projections using graphics

hardware. In I3D ’08: Proceedings of the 2008 sym-

posium on Interactive 3D graphics and games, pages

107–114, New York, NY, USA. ACM.

Goral, C. M., Torrance, K. E., Greenberg, D. P., and Bat-

taile, B. (1984). Modeling the interaction of light

between diffuse surfaces. In SIGGRAPH ’84: Pro-

ceedings of the 11th annual conference on Computer

graphics and interactive techniques, pages 213–222,

New York, NY, USA. ACM Press.

Hasselgren, J., Akenine-M

oller, T., and Ohlsson, L. (2005).

Conservative rasterization. In GPU Gems 2. Adison-

Wesley.

Heidrich, W. and Seidel, H.-P. (1998). View-independent

environment maps. In HWWS ’98: Proceedings of

the ACM SIGGRAPH/EUROGRAPHICS workshop on

Graphics hardware, pages 39–ff., New York, NY,

USA. ACM.

Kautz, J., Lehtinen, J., and Aila, T. (2004). Hemispherical

rasterization for self-shadowing of dynamic objects.

In Proceedings of Eurographics Symposium on Ren-

dering 2004, pages 179–184. Eurographics Associa-

tion.

Nielsen, K. H. and Christensen, N. J. (2002). Fast texture-

based form factor calculations for radiosity using

graphics hardware. J. Graph. Tools, 6(4):1–12.

Segal, M. and Akeley, K. (2003). The OpenGL Graphics

System: A Speciﬁcation (Version 2.0). Silicon Graph-

ics, Inc.

Sillion, F. and Puech, C. (1989). A general two-pass method

integrating specular and diffuse reﬂection. In SIG-

GRAPH ’89: Proceedings of the 16th annual con-

ference on Computer graphics and interactive tech-

niques, pages 335–344, New York, NY, USA. ACM.

Spencer, S. (1992). The hemisphere radiosity method: a tale

of two algorithms. Photorealism in Computer Graph-

ics, pages 127–135.

Wallner, G. (2008). GPU radiosity for triangular meshes

with support of normal mapping and arbitrary light

distributions. In Journal of WSCG, volume 16.

Wallner, G. (2009). An extended gpu radiosity solver: In-

cluding diffuse and specular reﬂectance and transmis-

sion. The Visual Computer, 25(5-7):529–537.

Willmott, A. J. and Heckbert, P. S. (1997). An empirical

comparison of radiosity algorithms. Technical report,

School of Computer Science, Carnegie Mellon Uni-

versity.

Yee, H. (2004). A perceptual metric for production testing.

Journal of graphics, gpu, and game tools, 9(4):33–40.

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

232