UNSUPERVISED IMAGE SEGMENTATION BASED ON THE

MULTI-RESOLUTION INTEGRATION OF ADAPTIVE LOCAL

TEXTURE DESCRIPTORS

Dana E. Ilea, Paul F. Whelan and Ovidiu Ghita

Centre for Image Processing & Analysis (CIPA), Dublin City University, Glasnevin, Dublin 9, Ireland

Keywords: Texture Segmentation, Multi-resolution Integration, Image Orientation, Texture Distribution.

Abstract: The major aim of this paper consists of a comprehensive quantitative evaluation of adaptive texture

descriptors when integrated into an unsupervised image segmentation framework. The techniques involved

in this evaluation are: the standard and rotation invariant Local Binary Pattern (LBP) operators, multi-

channel texture decomposition based on Gabor filters and a recently proposed technique that analyses the

distribution of dominant image orientations at both micro and macro levels. The motivation to investigate

these texture analysis approaches is twofold: (a) they evaluate the texture information at micro-level in

small neighborhoods and (b) the distributions of the local features calculated from texture units describe the

texture at macro-level. This adaptive scenario facilitates the integration of the texture descriptors into an

unsupervised clustering based segmentation scheme that embeds a multi-resolution approach. The

conducted experiments evaluate the performance of these techniques and also analyse the influence of

important parameters (such as scale, frequency and orientation) upon the segmentation results.

1 INTRODUCTION

Texture-based image segmentation represents a

major field of research in the area of computer

vision that has been intensively investigated for

more than three decades. This has been motivated by

the fact that the robust detection of texture

primitives in digital images plays a key role in the

identification of the constituent image regions.

Taking into consideration the large spectrum of

applications based on texture analysis, an impressive

number of approaches has been published in the

computer vision literature. As indicated in several

reviews on texture-based segmentation (Tuceryan

and Jain, 1998; Materka and Strzelecki, 1998) the

existent techniques can be classified into four major

categories: statistical, model-based, signal

processing and structural. From these approaches

most attention received the statistical and signal

processing texture extraction methods.

Statistical methods are based on the evaluation of

the spatial distributions and relationships between

the pixel intensities in the image. Relevant statistical

texture analysis techniques include the

autocorrelation function (Haralick, 1979), texture

energy features (Laws, 1980), grey-level co-

occurrence matrices (Haralick, 1979) and Local

Binary Patterns (Ojala and Pietikainen, 1999). Based

on the studies detailed in relevant papers focused on

statistical texture analysis it can be concluded that

these methods return adequate results when applied

to synthetic images, but their performance is limited

when applied to complex textured images.

To address some of the limitations associated

with standard statistical texture analysis techniques,

a non-parametric approach that analyses the texture

at micro-level based on the calculation of the Local

Binary Patterns (LBP) has been introduced by Ojala

and Pietikainen, 1999. This approach attempts to

decompose the texture into small units where the

texture features are represented by the distribution of

the LBP values. In (Ojala et al, 2002) the authors

extended the initial LBP approach to address its

sensitivity to rotation by introducing a new multi-

resolution rotational invariant LBP texture descriptor

whose performance was evaluated on standard

texture databases.

The signal processing methods represent another

important category of texture analysis techniques.

These techniques were developed as a consequence

of the psychophysical investigations that indicated

134

Ilea D., Whelan P. and Ghita O. (2010).

UNSUPERVISED IMAGE SEGMENTATION BASED ON THE MULTI-RESOLUTION INTEGRATION OF ADAPTIVE LOCAL TEXTURE DESCRIPTORS.

In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 134-141

DOI: 10.5220/0002822301340141

 SciTePress

that the human brain performs a frequency analysis

of the image perceived by the retina. Building on

this concept, the signal processing techniques

formulate the texture extraction in terms of the

frequency information associated with the texture

primitives present in digital images. Representative

methods that belong to this category are: spatial

domain filtering, Fourier analysis, Gabor filtering

and Wavelet analysis. Among these signal

processing methods, the approach that involves

filtering an image with a bank of Gabor filters has

gained the largest interest from the vision

researchers (Bovik et al, 1990; Jain and Farrokhnia,

1991; Hofmann et al, 1998, Randen and Husoy,

1999). This approach implements a multi-channel

texture decomposition and it is achieved by filtering

the input image with 2D Gabor filter banks. (Bovik

et al, 1990) used quadrature Gabor filters to segment

images defined by oriented textures. The main

conclusion resulting from their investigation is that

the spectral difference sampled by narrow band

filters provides sufficient information for texture

discrimination. (Jain and Farrokhnia, 1991) followed

a similar approach and developed a multi-channel

Gabor filtering technique that was applied for image

segmentation. In their paper, each filtered image was

subjected to a non-linear transform and the energy

was calculated within a pre-defined window around

each pixel in the image. The energy features were

afterwards clustered using a standard algorithm to

obtain the segmented image. This approach was

further advanced by (Randen and Husoy, 1999)

while noting that filtering the image with a bank of

Gabor filters or filters derived from Wavelet

transform is computationally intensive. In their

paper they proposed a new methodology to compute

optimised filters for texture discrimination that

requires a reduced number of filters than the

standard implementation developed by Jain and

Farrokhnia. A different segmentation strategy is

proposed by (Hofmann et al, 1998) where the texture

segmentation is formulated as a data clustering

problem. In their approach the dissimilarities

between pairs of textured regions are computed from

a multi-scale Gabor filtered image representation.

The resulting unsupervised segmentation scheme

was successfully applied on both Brodatz textures

and natural images.

Recently a novel hybrid statistical-structural

approach was proposed where the texture is

described in terms of the distribution of edge

orientations calculated at micro and macro-level for

all pixels in the image (Ilea et al, 2008; Ghita et al,

2008). The quantitative evaluations were conducted

on standard texture databases and the results

indicated that the local image orientation based

descriptor has a high discriminative power in the

context of texture classification. In this study we will

investigate its discrimination when applied to the

unsupervised segmentation of complex textural

arrangements.

The unsupervised segmentation process is in

particular challenging since the texture attributes are

not uniformly distributed within image areas defined

by similar objects and often the strength of the

texture can vary considerably from image to image.

In addition to this, complications added by the

uneven illumination, perspective and scale

distortions make the process of identifying the

homogeneous image regions with similar texture

characteristics extremely difficult. The quantitative

evaluation of the texture extraction techniques

investigated in this paper was carried out using a

segmentation framework similar to the one proposed

in (Ilea and Whelan, 2009). The selection of this

clustering-based segmentation technique for texture

segmentation is justified as it provides an attractive

platform for generalization and it also performs a

global data optimization.

The selection of the texture analysis techniques

evaluated in this study (the Local Binary Pattern

Operators, texture decomposition using Gabor

filtering and local orientation-based texture

descriptor) is also justified, as they allow an adaptive

texture analysis (at micro and macro-level) when

integrated into an unsupervised clustering approach.

The adaptive approach considered in this paper

provides a robust scenario for texture segmentation

and together with a comprehensive numerical

evaluation of the above mentioned methods it

represents a contribution of this paper in the study of

texture features segmentation.

This paper is organised as follows. Section 2

briefly introduces the texture analysis methods

investigated in this study and discusses the

motivation behind their selection. Section 3

describes the experimental setup and presents the

numerical evaluation followed by a discussion of the

obtained results. Section 4 concludes the paper.

2 EVALUATED TEXTURE

EXTRACTION METHODS

The Standard LBP/C Operator - The LBP

operator (Ojala and Pietikainen, 1999) is a powerful

texture descriptor as it analyses the texture at micro-

UNSUPERVISED IMAGE SEGMENTATION BASED ON THE MULTI-RESOLUTION INTEGRATION OF

ADAPTIVE LOCAL TEXTURE DESCRIPTORS

135

level, but at the same time the macro characteristics

of texture are sampled by the distribution of the LBP

values. The LBP texture unit is calculated by

thresholding the values of the pixels in a 3×3

neighbourhood with respect to the value of the

central pixel, while the LBP value is calculated by

multiplying the elements of the texture unit with

binomial weights (that are powers of 2 with respect

to the position of the pixels in the neighbourhood)

and summing the result.

To further improve the robustness of the LBP

operator and allow the sampling of the illumination

offsets between different textures, the standard LBP

operator is used in conjunction with the contrast

operator, C. The contrast measure C is calculated as

the difference between the average grey-level of the

pixels with values 1 and the pixels with values 0

contained in the 3×3 texture unit. The main

advantage of analysing the texture using the

distribution of LBP/C values is given by the fact that

they can be used to discriminate textures in the input

image regardless the region size. The distribution of

the LBP/C values calculated over an image region

represents the texture spectrum that can be defined

as a joint histogram of size (256 + bins), where the

first 256 bins are required by the distribution of the

LBP values and bins represents the number of bins

employed to sample the contrast measure. Based on

the experiments performed by Ojala and Pietikainen,

the best results are obtained when the contrast

distribution is quantised into 4 to 16 bins. The

optimal selection of the number of bins is a difficult

issue since for low values of bins the histogram will

lack resolution, while for high values of bins the

histogram will become sparse and unstable. Based

on experimentation it has been demonstrated that a

quantisation of the contrast measure in 8 bins returns

the best results.

The Rotation Invariant LBP Operator (LBP

) -

The standard LBP values calculated for each texture

unit are sensitive to texture orientation. This is

motivated by the fact that the elements of the texture

unit uniquely encode the position of each pixel in the

3×3 neighbourhood. To remove the sensitivity to

rotation, the texture descriptor is calculated within a

circular neighbourhood and the texture is evaluated

in terms of uniformity. A uniform pattern is defined

as the number of transitions between 0 and 1 in the

LBP mask obtained after thresholding the pixels

from the circular neighbourhood with the intensity

value of the central pixel. In this way, the authors

defined a pattern as uniform if the binary LBP

pattern has maximum two transitions; otherwise the

pattern is labelled as non-uniform. To improve its

discriminative power, the LBP

value is

complemented with the contrast measure that is

calculated as the variance of the pixels situated in

the LBP mask. For more details regarding the

calculation of the LBP operators, the reader can refer

to (Ojala and Pietikainen, 1999; Ojala et al, 2002).

Texture Analysis using Gabor Filters is an

approach that implements a multi-channel texture

decomposition and is achieved by filtering the input

image with a two-dimensional (2D) Gabor filter

bank that was introduced by (Daugman, 1988) and

later applied to texture segmentation by (Jain and

Farrokhnia, 1991). The 2D Gabor function that is

used to implement the even-symmetric 2D discrete

filters can be written as follows:











 '2cos)

exp(),(

yxG

(1)

In equation (1)



sincos

yxx  ,



cossin

yxy  , σ is the scale parameter of the

Gabor filter,



is the orientation and f is the

frequency parameter that controls the number of

cycles of the cosine function within the envelope of

the 2D Gaussian (



is the phase offset and it is

usually set to zero to implement 2D even-symmetric

filters). The parameters of the Gabor filters are

chosen to optimise the trade-off between spectral

selectivity and the size of the bank of filters.

Typically, the central frequencies are selected to be

one octave apart and for each central frequency is

constructed a set of filters corresponding to four (0

, 90

, 135

) or six orientations (0

, 30

, 60

, 90

120

, 150

Texture Extraction using the Dominant Image

Orientation at Micro and Macro-levels is an

approach defined in terms of the distribution of the

dominant edge orientations at micro and macro-level

and was introduced in (Ilea et al, 2008; Ghita et al,

2008). In this regard, the orientation for each pixel in

the image is extracted using the partial derivatives of

the Gaussian function (G) while the main focus is

the evaluation of the local dominant orientation.

An important parameter is the scale (σ) of the

Gaussian function and its role is to control the

amount of noise reduction. After the calculation of

the partial derivatives, the weak edge responses were

eliminated by applying a non-maxima suppression

procedure (Canny, 1986) and the edge orientation is

calculated. As indicated in (Ilea et al, 2008), the

problem of analysing the texture orientation at a

given observation scale is not a straightforward task

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

136

as the orientation of textures may be isotropic at

macro-level but having a strong orientation at micro-

level. Therefore, we propose to evaluate the

dominant orientation of the texture calculated at

micro-level for all texture units that are defined as

the local neighbourhood around each pixel in the

image, while the distribution of the dominant

orientations calculated for all texture units is

employed to capture the dominant orientation of

texture at macro-level.

In this implementation, the orientation of the

texture is determined by constructing the histogram

of orientations for all pixels in the local

neighbourhood and the dominant orientation is

selected as the dominant peak in the histogram as

follows,





















)2/(

)),,(( ),,(

][0,2 D ,),,(),(

iyxiyxh

iyxhyxH







(2)





























),(

yxfG

arctgyx



and

)max(arg



 H

(3)

In equations (2) and (3), Θ is the local

orientation, the symbol  defines the convolution

operation,

yGG

 / , xGG

 / , f(x,y) is the

pixel value at position (x,y) in the original image, i is

the orientation bin, D defines the orientation domain,



H (x,y) is the distribution of the local orientations

calculated around pixels situated at positions (x,y)

and Θ

is the dominant texture orientation in the

neighbourhood w×w. The dominant orientation at

macro-level (H

Θd

) is estimated by the distribution of

the local dominant orientations that are determined

over the region of interest as follows,













diyxH



)),,((



(4)

where Γ is the image domain. In equation (4) it

should be noted that the texture orientation is

sampled at a pre-defined observation scale that is

controlled by the size of the neighbourhood w×w.

The dominant orientation is not robust in

sampling the difference between textures that are

subjected to illumination variation. Thus, the local

texture orientation is augmented with measures such

as local orientation coherence and contrast (C) that

are calculated in the local neighbourhood w×w

where the dominant orientation of the texture has

been estimated. The contrast measure (C) is sampled

by the mean grey-scale value calculated in the w×w

neighbourhood and the orientation coherence (Θ

) is

calculated using the weighted standard deviation of

the edge orientation of all the pixels in the

neighbourhood w×w.

3 EXPERIMENTS AND RESULTS

In this paper, we have modified the computational

architecture of the segmentation framework

proposed in (Ilea and Whelan, 2008) in order to

provide a robust scenario for texture segmentation.

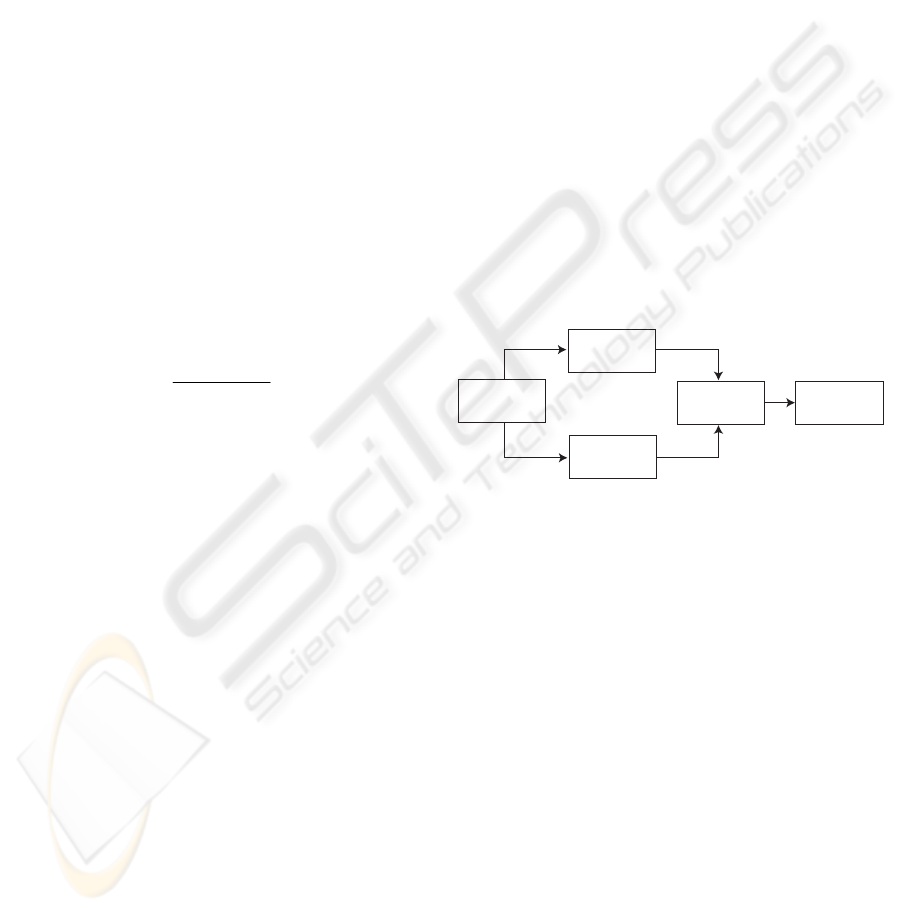
The main steps of the proposed texture segmentation

algorithm are illustrated in Figure 1. It is important

to mention that the texture features are

independently extracted from the luminance

component of the input image to exclusively

evaluate the texture information.

Input Image

Number of

clusters

Texture

Features

ASKM

Segmented

Image

Figure 1: Overview of the texture segmentation algorithm.

The Adaptive Spatial K-means (ASKM)

clustering is the main component of the

segmentation method. The main idea behind ASKM

is to minimise an objective function J

based on the

fitting between the local texture distributions

calculated for each pixel in the texture image and

global texture distributions calculated for each

cluster as follows,





 



























width

height

HyxHKSJ

11 1

]2525,...,33[

),,(min

(5)

In equation (5), k is the number of clusters, s×s

defines the size of the local window,

),( yxH



is the

local texture distribution calculated for the pixel at

position (x,y) and

H is the texture distribution for

the cluster with index i respectively. The number of

clusters k is automatically calculated in conjunction

with the number of textures in the image as indicated

UNSUPERVISED IMAGE SEGMENTATION BASED ON THE MULTI-RESOLUTION INTEGRATION OF

ADAPTIVE LOCAL TEXTURE DESCRIPTORS

137

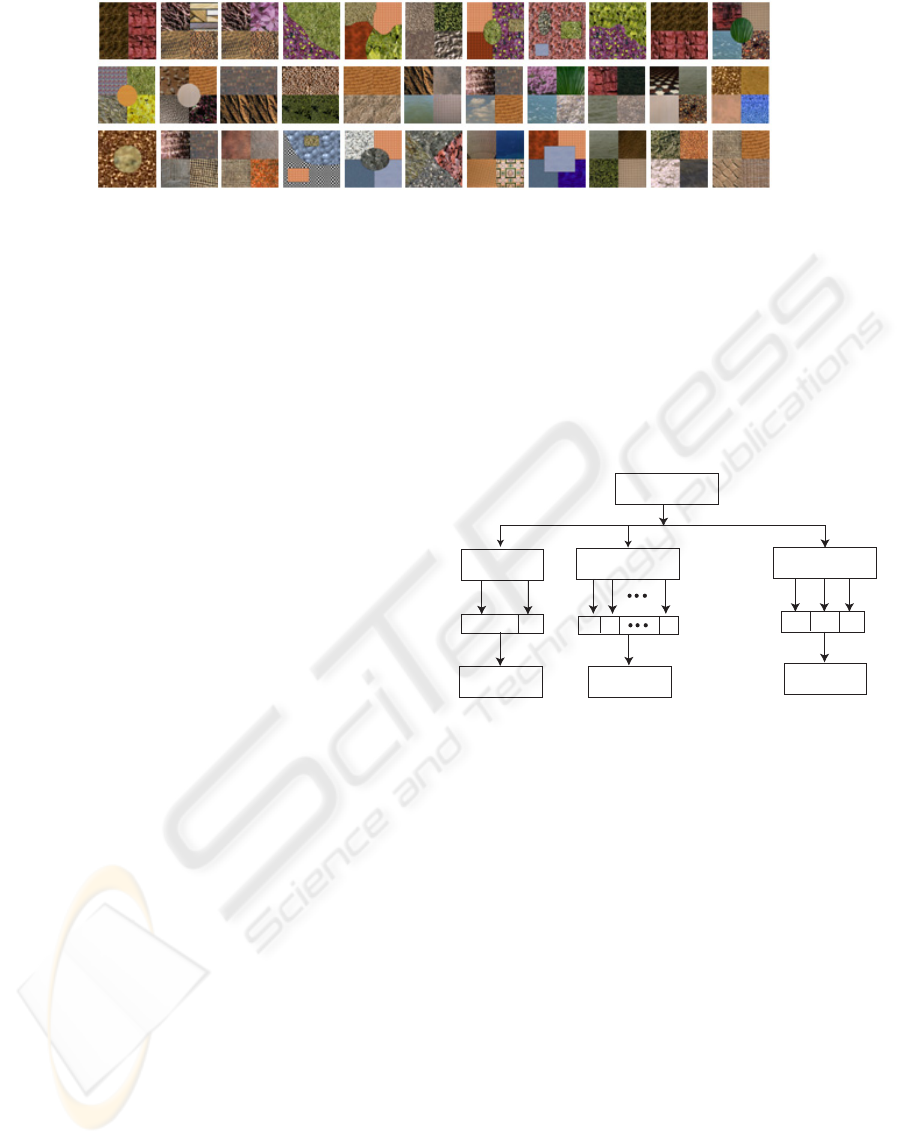
Figure 2: The database of 33 mosaic images used in our experiments.

in (Ilea and Whelan, 2008). The similarity between

the local texture distribution and the global texture

distribution of the clusters is evaluated using the

Kolmogorov-Smirnov (KS) metric (Rubner et al,

2001). The fitting between the local texture

distributions and global texture distributions of the

clusters is performed adaptively for multiple

window sizes in the interval [3×3] to [25×25]. While

textures in the image are not uniform, the multi-

resolution approach detailed in this paper offers an

attractive scheme for texture segmentation as it

allows the variation of the window size until the best

fit between the global and local texture distributions

is achieved.

Experimental Setup - Since the ground truth data

associated with complex natural images is difficult

to estimate and its extraction is highly influenced by

the subjectivity of the human operator, the texture

segmentation evaluation was performed on mosaic

data where the ground truth is unambiguous.

Therefore, the segmentation algorithm described in

the previous section was applied to a database of 33

mosaic images (image size 184×184) that were

created by mixing complex textures from (VisTex

2000) and Photoshop databases. The mosaics used in

these experiments consist of various texture

arrangements that also include images where the

borders between different regions are irregular. The

suite of 33 mosaic images is depicted in Figure 2.

The quantitative measurements were carried out

using the Probabilistic Rand Index (PR)

(Unnikrishnan and Hebert, 2005) that measures the

agreement between the segmented result and the

ground truth data and takes values in the range [0,

1]. A higher PR value indicates a better match

between the segmented result and the ground truth

data. The PR Index is defined in the appendix of this

paper. In this study, for every analysed texture

analysis technique, the PR mean and standard

deviation were computed for all images in the

database.The construction of the texture vectors is

illustrated in Figure 3. It can be noticed that the

feature vectors are defined either by the LPB/C joint

distributions or by the distributions calculated from

the responses obtained after filtering the image with

the multi-channel filter bank (the intensity values of

the filtered images were normalised in the interval

[0, 255] so the size of the feature vector is

256×number of filters in the filter bank). For the

edge orientation-based technique, the texture vector

is given by the joint distribution defined by the

dominant orientation (Θ

), the contrast (C) and the

orientation coherence (Θ

Texture Features

LBP operators

Gabor Filters

LBP

Contrast

ASKM

LBP C

4 or 6 oriented filters

ASKM

Local Orientation

Features

ASKM

Figure 3: The calculation of the texture distributions.

3.1 Results Returned by the LBP

Technique

The first set of tests evaluates the segmentation

performance when using the standard Local Binary Pattern

(LBP) and the rotation invariant LBP

8,1

, LBP

16,2

LBP

24,3

texture descriptors. As indicated above, the

experiments were performed on a database consisting of

mosaic images and the numerical results are illustrated in

Table 1 (the LBP

P,R

defines the rotation invariant LBP

operator where P is the number of pixels in the LBP mask

and R is the radius of the mask ).

The results illustrated in Table 1 indicate that the

LBP/C operator provides better discrimination in its

standard form than the rotation invariant LBP

8,1

LBP

16,2

, LBP

24,3

descriptors. The LBP/C operator

returned the highest PR values for 21 out of 33

mosaic images, while the LBP

8,1

operator returned

the lowest PR values for 13 images out of 33. The

drop in segmentation accuracy for rotation invariant

LBP descriptors indicates that the invariance to

rotation, as expected, is attained at the expense of

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

138

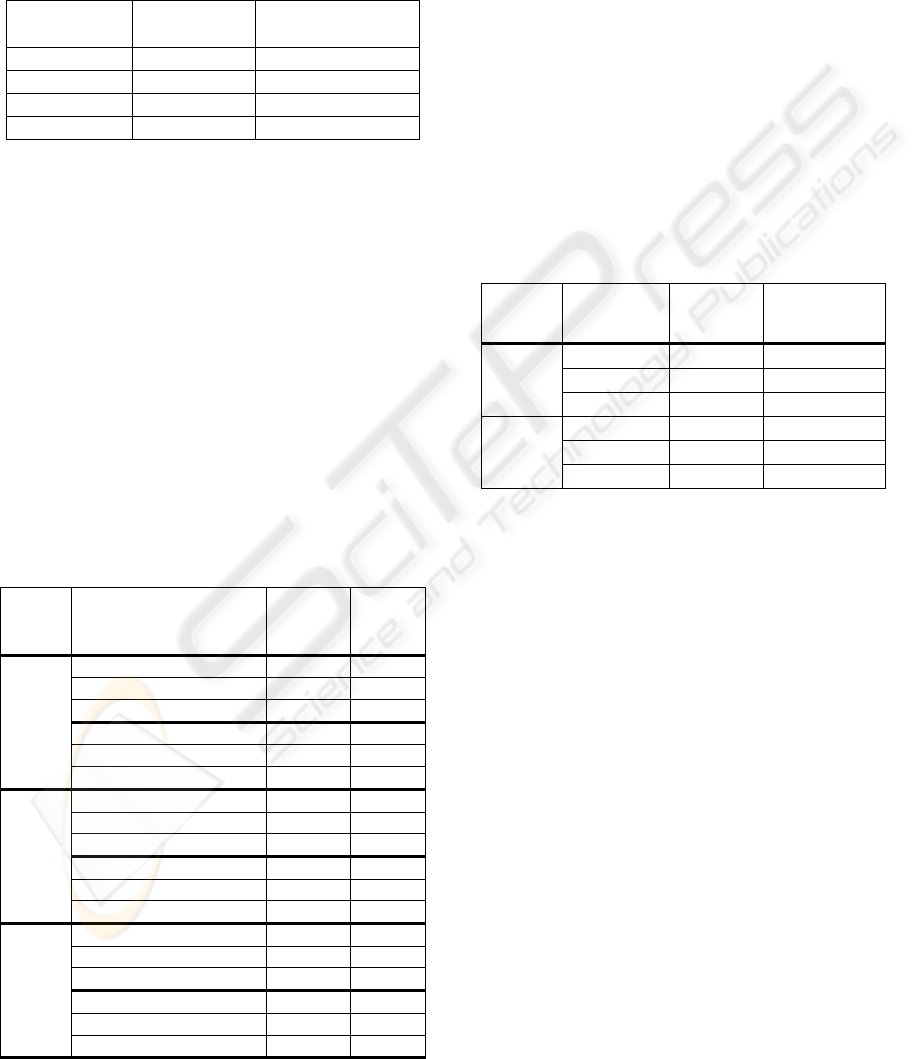
the loss in discriminative power. This conclusion is

justified since the LBP uniform patterns are not able

to sample the directional characteristics of the

texture.

Table 1: Quantitative results when the LBP/C texture

descriptors were evaluated in the proposed segmentation

framework.

Method PR

mean

standard_deviation

LBP/C 0.84 0.12

LBP

/C 0.80 0.11

LBP

/C 0.82 0.09

LBP

/C 0.82 0.12

3.2 Results Returned by the Gabor

Filtering Technique

In order to evaluate the multi-channel texture

decomposition scheme based on Gabor filtering, the

input image has been processed with a small bank of

filters with four (0

, 45

, 90

, 135

) and six (0

, 30

, 90

, 120

, 150

) orientations. The central

frequency and the scale parameters were also varied.

The standard deviation (scale) parameter was set to

the values 1.0, 2.0 and 3.0 respectively, while the

central frequency parameter was varied by setting it

to the following values 1.5/2π, 2.0/2π and 2.5/2π,

respectively.

Table 2: Quantitative results when the Gabor filtering

(GF) technique was evaluated in the proposed

segmentation framework.

Scale (σ)

Method

mean

st_dev

σ= 1.0

GF f

= 1.5/2π, 4 angles 0.46 0.24

GF f

= 2.0/2π, 4 angles 0.61 0.17

GF f

= 2.5/2π, 4 angles 0.81 0.12

GF f

= 1.5/2π, 6 angles 0.50 0.26

GF f

= 2.0/2π, 6 angles 0.62 0.18

GF f

= 2.5/2π, 6 angles 0.81 0.12

σ = 2.0

GF f

= 1.5/2π, 4 angles 0.65 0.17

GF f

= 2.0/2π, 4 angles 0.83 0.10

GF f

= 2.5/2π, 4 angles 0.85 0.08

GF f

= 1.5/2π, 6 angles 0.65 0.17

GF f

= 2.0/2π, 6 angles 0.84 0.09

GF f

= 2.5/2π, 6 angles 0.85 0.08

σ = 3.0

GF f

= 1.5/2π, 4 angles 0.78 0.13

GF f

= 2.0/2π, 4 angles 0.85 0.08

GF f

= 2.5/2π, 4 angles 0.85 0.11

GF f

= 1.5/2π, 6 angles 0.79 0.12

GF f

= 2.0/2π, 6 angles 0.84 0.08

GF f

= 2.5/2π, 6 angles 0.86 0.08

3.3 Results Returned by the Local

Orientation-based Texture

Descriptor

In (Ilea et al, 2008; Ghita et al, 2008) a texture

descriptor based on the evaluation of the dominant

image orientation calculated at micro and macro-

level was proposed. In this section, experimental

results that quantify the performance of the image

orientation based texture descriptor in the

segmentation process are provided. For these

experiments the value of the parameter σ (that sets

the scale of the derivative of the Gaussian function)

is set to 0.5 and 1.0. The experimental results

illustrated in Table 3 indicate that the optimal results

are obtained when the scale parameter σ is set to 0.5.

Table 3: Quantitative results for the local orientation based

texture extraction technique when the window size is

varied.

Scale

(σ)

Window

size

mean

standard_deviation

σ = 0.5

3×3 0.83 0.12

7×7

0.82 0.11

11×11

0.82 0.12

σ = 1.0

3×3

0.81 0.12

7×7

0.81 0.12

11×11

0.81 0.11

There are two reasons behind the selection of this

value for the σ parameter. The first is motivated by

the fact that with the increase in the value of the

scale parameter the edges derived from weak

textures are eliminated and the second reason

consists in the requirement to increase the size of the

derivative of the Gaussian filters with the increase of

the scale parameter σ. The feature vectors for the

edge orientation technique are formed by the joint

distributions (see Figure 3) constructed using the

dominant orientation, the contrast and the orientation

coherence. The experiments were conducted on the

mosaic database when the size of the texture unit

w×w is varied. The experimental data shown in

Table 3 indicates that optimal performance is

obtained when the texture orientation is sampled in

small texture units and these results are motivated by

the fact that the texture orientation is best analysed

at micro-level.

UNSUPERVISED IMAGE SEGMENTATION BASED ON THE MULTI-RESOLUTION INTEGRATION OF

ADAPTIVE LOCAL TEXTURE DESCRIPTORS

139

4 CONCLUSIONS

The aim of this paper was to evaluate the

performance of a number of statistical and signal

processing texture analysis techniques when applied

to image segmentation. The techniques evaluated in

this study are: the LBP/C operators, multi-channel

texture decomposition based on Gabor filter banks

and a recently proposed texture analysis technique

based on the evaluation of the image orientation at

micro and macro-level. The main novelty associated

with this work resides in the evaluation of the

analysed texture descriptors in a multi-resolution

framework offered by the proposed texture

segmentation algorithm and in the evaluation of the

experimental results when the parameters associated

with these techniques are varied. Our experiments

show that the method based on texture

decomposition using Gabor filters marginally

outperformed the other analysed techniques. The

experimental data reinforced the concept that texture

is an important attribute of digital images and it also

indicates that the local orientation is the dominant

feature that provides the primary discrimination

between textures.

ACKNOWLEDGEMENTS

This work was funded in part by the HEA PRTLI IV

National Biophotonics & Imaging Platform Ireland

(NBIPI) and the Science Foundation Ireland

(Research Frontiers Programme).

REFERENCES

Bovik, A. C., Clark, M., Geisler, W. S.: Multi-channel

Texture Analysis Using Localized Spatial Filters.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, Vol. 12, No. 1 (1990) 55-73

Canny, J.: A Computational Approach to Edge Detection.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, Vol. 8, No. 6 (1986) 679-698

Daugman, J. G.: Complete Discrete 2D Gabor Transforms

by Neural Networks for Image Analysis and

Compression. IEEE Transactions on Acoustics,

Speech and Signal Processing, Vol. 36, No. 7 (1988)

1169-1179

Ghita, O., Whelan, P. F., Ilea, D. E.: Multi-resolution

Texture Classification Based on Local Image

Orientation. In Proceedings of the 5

International

Conference on Image Analysis and Recognition

(ICIAR), Portugal (25-27 July, 2008) 688-696

Haralick, R. M.: Statistical and Structural Approaches to

Texture. In Proceedings of the IEEE, Vol. 67, No. 5

(1979) 786-804

Hofmann, T., Puzicha, J., Buhmann, J. M.: Unsupervised

Texture Segmentation in a Deterministic Annealing

Framework. IEEE Transactions on Pattern Analysis

and Machine Intelligence, Vol. 20, No. 8 (1998) 803-

818

Ilea, D. E., Ghita, O., Whelan, P. F.: Evaluation of Local

Orientation for Texture Classification. In Proceedings

of the 3

International Conference on Computer

Vision Theory and Applications (VISAPP), Portugal

(22 - 25 January 2008) 357-364

Ilea, D. E., Whelan, P. F.: CTex - An Adaptive

Unsupervised Segmentation Algorithm Based on

Colour-Texture Coherence. IEEE Transactions on

Image Processing, Vol. 17, No. 10 (2008) 1926-1939

Jain, A. K., Farrokhnia, F.: Unsupervised Texture

Segmentation Using Gabor Filters. Pattern

Recognition, Vol. 24, No. 12 (1991) 1167-1186

Laws, K. L.: Rapid Texture Identification. In Proceedings

of the SPIE Conference on Image Processing for

Missile Guidance, Vol. 238 (1980) 376-380

Materka, A., Strzelecki M.: Texture Analysis Methods – A

Review. Technical Report, University of Lodz, Cost

B11 Report (1998)

Ojala, T., Pietikainen, M.: Unsupervised Texture

Segmentation Using Feature Distributions. Pattern

Recognition, Vol. 32, No. 3 (1999) 477-486

Ojala, T., Pietikainen, M., Maenpaa, T.: Multiresolution

Grey-scale and Rotation Invariant Texture

Classification with Local Binary Patterns. IEEE

Transactions on Pattern Analysis and Machine

Intelligence, Vol. 24, No. 7 (2002) 971-987

Randen, T., Husoy, J. H.: Texture Segmentation Using

Filters with Optimised Energy Separation. IEEE

Transactions on Image Processing, Vol. 8, No. 4

(1999) 571-582

Rubner, Y., Puzicha, J., Tomasi, C., Buhmann, J. M.:

Empirical Evaluation of Dissimilarity Measures for

Colour and Texture. Computer Vision and Image

Understanding, Vol. 84, No. 1 (2001) 25-43

Tuceryan, M., Jain, A. K.: Texture Analysis. In: Chen,

C.H., Pau, L.F., Wang, P.S.P. (eds.): Handbook of

Pattern Recognition and Computer Vision, World

Scientific Publishing (1998)

Vision Texture (VisTex) Database, Massachusetts Institute

of Technology, MediaLab. http://vismod.media.mit.

edu/vismod/imagery/VisionTexture/vistex.html

Unnikrishnan, R., Hebert, M.: Measures of Similarity. In

Proceedings of IEEE Workshop on Computer Vision

Applications, Vol. 1 (2005) 394 – 394

APPENDIX

The Probabilistic Rand index (PR) was proposed in

(Unnikrishnan and Hebert, 2005) with the aim of

obtaining a quantitative evaluation of the

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

140

segmentation result when compared to one or more

ground truth (manual) segmentations. Let S

test

be the

segmented image that will be compared against the

manually labelled set of ground truth images {S

,…, S

} (where G defines the total number of

manually segmented images). The segmentation

result is quantified as appropriate if it correctly

identifies the pairwise relationships between the

pixels as defined in the ground truth segmentations.

In other words, the pairwise labels

test

and

test

(corresponding to any pair of pixels x

, x

in the

segmented image S

test

)

are compared against the

pairwise labels

l and

l in the ground truth

segmentations and vice versa. Based on this

principle, the PR index is defined as follows:

























Gtest

pllpll

SSPR

testtesttesttest

...1

)1(

}){,(

(6)

In equation (6) N is the total number of pixels in

the image,





testtest

ll 

denotes the probability

that the pair of pixels x

and x

have the same label in

test

and p

represents the mean pixel pair

relationship between the ground truth images.











(7)

The PR index takes values in the interval [0, 1]

and a higher PR value indicates a better match

between the segmented result and the ground truth

data. The PR index takes the value 0 when there are

no similarities between the segmented result and the

set of manual segmentations and it takes the value 1

when all segmentations are identical.

UNSUPERVISED IMAGE SEGMENTATION BASED ON THE MULTI-RESOLUTION INTEGRATION OF

ADAPTIVE LOCAL TEXTURE DESCRIPTORS

141