TOWARDS GENERIC FITTING USING DISCRIMINATIVE ACTIVE

APPEARANCE MODELS EMBEDDED ON A RIEMANNIAN

MANIFOLD

Pedro Martins and Jorge Batista

∗

ISR-Institute of Systems and Robotics, Dep. of Electrical Engineering and Computers

FCTUC-University of Coimbra, Coimbra, Portugal

Keywords:

Active appearance models, Discriminative ﬁtting, Riemannian manifolds.

Abstract:

A solution for Discriminative Active Appearance Models is proposed. The model consists in a set of de-

scriptors which are covariances of multiple features evaluated over the neighborhood of the landmarks whose

locations are governed by a Point Distribution Model (PDM). The covariance matrices are a special set of

tensors that lie on a Riemannian manifold, which make it possible to measure the dissimilarity and to update

them, imposing the temporal appearance consistency. The discriminative ﬁtting method produce patch re-

sponse maps found by convolution around the current landmark position. Since the minimum of the responce

map isn’t always the correct solution due to detection ambiguities, our method ﬁnds candidates to solutions

based on a mean-shift algorithm, followed by an unsupervised clustering technique used to locate and group

the candidates. A mahalanobis based metric is used to select the best solution that is consistent with the PDM.

Finally the global PDM optimization step is performed using a weighted least-squares warp update, based on

the Lucas and Kanade framework. The weights were extracted from a landmark matching score statistics. The

effectiveness of the proposed approach was evaluated on unseen data on the challenging Talking Face video

sequence, demonstrating the improvement in performance.

1 INTRODUCTION

Facial image alignment is the key aspect in many

computer vision applications, such as tracking and

recognition. In the past years, most existing meth-

ods have used generative based methods, where

the shape and texture variation were learned from

training images. The Active Appearance Models

(AAM)(T.F.Cootes et al., 2001)(Matthews and Baker,

2004) is one of the most effective techniques with

respect to ﬁtting accuracy and efﬁciency. Although,

it consists on generative holistic representations (in

sense that all pixels belonging to the object are used).

Due to the generative nature, AAM is able to synthe-

size a high quality model where the data is used si-

multaneously during the ﬁtting, producing a high ac-

curacy ﬁtting. This representation generalization per-

forms poorly when the target exhibits large amounts

of variability, such as the case of the human face un-

der variations of identity, expression, pose, lighting or

non-rigid motion due to the huge dimensional repre-

∗

Work funded by FCT grant SFRH/BD/45178/2008.

sentation of the appearance (learnt from limited data).

The main drawback with the generative approaches

is that typically they only work well for the individ-

uals held in the training dataset(Gross et al., 2005)

due to the fact that the appearance is eigen based

and captured by a linear Principal Components Anal-

ysis (PCA). Various solutions were proposed to deal

with this limitation: Adaptive AAM(Batur and Hayes,

2005), Constrained AAM, that are mainly based on

online updating the Jacobian matrix. Other Adap-

tive AAM solutions (Sung and Kim, 2009) (Matthews

et al., 2004) consist on online incremental PCA.

Recently, discriminative based methods such as the

Constrained Local Model (CLM)(D.Cristinacce and

T.F.Cootes, 2008) or (Wang et al., 2008a) (Wang

et al., 2008b) have been proposed. These methods

use a set of discriminative template regions surround-

ing individual landmarks whose locations are gov-

erned by a Point Distribution Model (PDM). The ﬁt-

ting is based on an exhaustive local search around the

current landmark location, producing response maps

(for each landmark) and driving the parameters of the

PDM in order to maximize the sum of responses for

363

Martins P. and Batista J. (2010).

TOWARDS GENERIC FITTING USING DISCRIMINATIVE ACTIVE APPEARANCE MODELS EMBEDDED ON A RIEMANNIAN MANIFOLD.

In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 363-369

DOI: 10.5220/0002823603630369

 SciTePress

each point. Compared with the holistic representa-

tions, such as AAM, working at patch level offers ex-

tra ﬂexibilities. The parts-based representation im-

prove the model’s representation capacity, as it ac-

counts only for local correlations between pixel val-

ues and naturally is presents good performance in ﬁt-

ting unseen appearances in comparison with the lead-

ing holistic approaches. The CLM uses as patch de-

scriptors, normalized correlation response surfaces.

In (Wang et al., 2008a) (Wang et al., 2008b) the dis-

criminant descriptor is obtained using machine learn-

ing methods, i.e. a linear Support Vector Machines

(SVM), which require a extensive training, labeling

lots of positive and negative samples. Our approach

ﬁts on the discriminative class of methods where, like

the standard AAM, consists in two separated mod-

els: the shape and the appearance models. The shape

model is an ordinary PDM that deals with the posi-

tion of the landmarks. The appearance is composed

by a set of descriptors for each of the landmarks in

the PDM. The descriptors are covariance matrices of

multiple features evaluated on the surrounding loca-

tion of the landmarks. Since the covariance matrices

are a special set of tensors that lie on a Riemannian

manifold, it is possible to measure the dissimilarity

between two covariances, and also to update them,

imposing the temporal appearance consistency. The

method starts using a generic covariance (the aver-

age covariance observed in the training set) which is

then continuously updated. Although, like the pre-

vious methods (D.Cristinacce and T.F.Cootes, 2008)

(Wang et al., 2008a) (Wang et al., 2008b), the patch

response maps found by convolution around the cur-

rent landmark position suffers from detection ambi-

guities. It will be shown that the minimum (in covari-

ance dissimilarity) of the responce map isn’t always

the desired solution. A solution based on a mean-

shift algorithm is proposed, ﬁnding candidates to so-

lutions, followed by an unsupervised clustering tech-

nique(Figueiredo and Jain, 2002) locating and group-

ing the candidates. A mahalanobis based metric is

used to select the best solution consistent with the

PDM. Finally the global optimization step, solving

the PDM is performed using a weighted least-squares

warp update based on the Lucas and Kanade frame-

work(Baker and Matthews, 2004). The weights were

extracted from landmark matching score statistics.

This paper is organizedas follows: section 2 describes

background subjects required, namely the basics on

Riemann Manifolds and PDM building. In section 3

our approach is detailed presented, section 4 presents

experimental results and in section 5 conclusions are

presented.

2 BACKGROUND

2.1 Shape Model

The shape of a (2D) Point Distribution Model (PDM)

is deﬁned by the vertex locations of a mesh. The rep-

resentation used for a single v-point shape is a 2v vec-

tor given by s = (x

, . . . , x

, y

, . . . , y

)

. The PDM

training data consists of a set of annotated images

with the shape mesh marked (usually by hand). All

the shapes are then aligned to a common mean shape

using a Generalised Procrustes Analysis (GPA), re-

moving location, scale and rotation effects. Princi-

pal Components Analysis (PCA) are then applied to

the aligned shapes, resulting on the linear parametric

model s = s

+ Φp, where new shapes, s, are syn-

thesized by deforming the mean shape, s

, using a

weighted linear combination of eigenvectors, φ

, i =

1, . . . , n. n is the number of eigenvectors that holds

a user deﬁned variance, typically 95%. p is a vec-

tor of shape parameters which represents the weights.

See Figure 1-a)b)c). Notice that the GPA makes that

(a) (b) (c) (d) (e)

Figure 1: a) Shape raw data. b) Aligned landMarks after

GPA. c) Shape covariance Σ

around each landmark. d)

Patches P

, l × l around each landmark. e) Illustration of

ﬁnding the average covariance C

for a speciﬁc patch (left

side of left eye corner). Each training image provide a nor-

malized patch. The covariances for the feature vector f are

evaluated and using eq.2, C

is found.

the PDM do not model the similarity transformation

which is required onto the target image. To overcome

this we use the approach proposed by (Matthews and

Baker, 2004), i.e., we include a special set of 4 eigen-

vectors ψ

, . . . , φ

. A full shape is then described

by a linear system s = s

∑

i=1

∑

j=1

where q represents the 2D pose parameters with q

scos(θ) − 1, q

= ssin(θ), q

= t

, q

= t

where s,

θ, (t

, t

) represents the scale, rotation and translation

w.r.t. the base mesh s

2.2 Texture Model - Covariance of

Features

The discriminative appearance model used is based

on a descriptor of the texture around each one of the

v landmarks. Inspired on the work of (Porikli et al.,

2006), a quadrangular region P (patch) with size l is

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

364

sampled around each landmark. See Figure 1-d. On

each of the regions, P

, k = 1, . . . , v, several features

f are extracted for each pixel x = (x, y)

, ∈ P

where

f = [x y I

+ I

arctan





+ I

The features used are the pixel position (x, y), hori-

zontal and vertical gradients (I

, I

), gradient magni-

tude, gradient phase, and the Laplacian. The main

advantages of our formulation is that it can always

allow more features in order to ﬁnd a better descrip-

tor for P

without changing the remaining formula-

tion. Stacking all measures of f, i.e. F

= f ∈ P

, the

d × d covariance matrix for the features is given by

−1

∑

i=1

− µ

)(F

− µ

)

where µ

the vector of feature means within the region P

. The

covariance C

is used as region descriptor (which rep-

resents the correlations between the features f for the

entire region P

). The main advantage of using co-

variances of features is that, if they are positive deﬁ-

nite matrices, C

lie in a Riemannian Manifold and is

possible to measure dissimilarities and make updates.

2.2.1 Dissimilarity between Covariances

The covariance matrices do not lie on Euclidean

space. Based on the Riemannian invariants, a distance

metric(Pennec et al., 2006) is used. The dissimilarity

between two covariances matrices C

and C

is given

ρ(C

, C

) =

∑

i=1

, C

) (1)

where λ

, C

)

i=1,...,m

are the generalized eigenval-

ues of C

and C

, computed from λ

− C

0, i = 1, ..., d and x

6= 0 are the generalized eigenvec-

tors. Note that ρ(C

, C

) ≥ 0.

2.2.2 Updating Covariances - Finding C

The mean of the points on the manifold minimizes

the L

norm of C = argmin

∑

t=1

(C, C

). (Pennec

et al., 2006) proposed a gradient descent approach to

compute the C by C

i+1

= exp



∑

t=1

log

)



To prevent the model from contamination, it is possi-

ble to weight the data points by a factor proportional

to its similarity to the current model, resulting

i+1

= exp

∗

∑

t=1

−1

, C

∗

)log

)

(2)

where ρ is deﬁned in eq.1, ρ

∗

∑

t=1

−1

, C

∗

) and

∗

is the model computed at the T previous frames.

Each training image provide a set of v covariances

matrices, C

(for each landmark k). For N images

in the set, the average covariance matrix, C

, is com-

puted over the Riemannian Manifold using eq.2. See

Figure 1-e for a graphical interpretation of this pro-

cess. The mean covariance, C

, is used as the initial

descriptor for that speciﬁc landmark k.

2.3 Image Normalization - Afﬁne Warp

Since the covariance isn’t invariant to scale and ro-

tation effects, a normalization at image level is re-

quired. The normalization is based on an afﬁne warp

of the entire image in a way that the current mesh s is

mapped into the reference base mesh s

. At a glance,

it seems that a similarity warp will be sufﬁcient due to

the nature of this problem, but experimentally it was

concluded that the two extra degrees of freedom of

the afﬁne model provide a better quality in covariance

matching.

3 OUR APPROACH - DAAM-R

After building the PDM and evaluating the average

covariance C

for each landmark k (in a training

stage), ﬁtting the Discriminative AAM embedded on

a Riemannian Manifold (DAAM-R) consists on ﬁnd-

ing k local optimal displacements, ∆x

†

, from the PDM

current mesh position s. The local updates, expressed

in the base mesh, will be constrained to lie in the

subspace spanned by Φ by an nonlinear optimization

based on the Lucas Kanade framework(Baker et al.,

2003). (See section 3.1). The goal is to ﬁnd the devi-

ation from the PDM, ∆x, for each landmark. The se-

quential steps of proposed approach are enumerated

and Figure 2 shows the overall view for the ﬁtting

methodology. (1) Scanning by convolution around

a local region ﬁnding a response map of covariances

dissimilarities (Figure 2-a). (2) The minimum of the

responce map, i.e. the lower dissimilarity, doesn’t

always correspond to the correct landmark location.

Actually, in some cases it can be a poor estimate,

since the features consists of small image patches that

often contain limited structure, leading to detection

ambiguities. It is however assumed that the correct

solution is a local minima. A modiﬁed version of a

mean-shift algorithm (section 3.2) is used to detect all

the local minima (see Figure 2-b) providing a set of

candidates to the landmark solution. (3) The mean-

shift will produce clusters with the candidates to so-

lutions, ∆x

∗

. At this stage is important to deﬁne the

number and location of these clusters. For this pro-

pose an unsupervised clustering method proposed by

TOWARDS GENERIC FITTING USING DISCRIMINATIVE ACTIVE APPEARANCE MODELS EMBEDDED ON A

RIEMANNIAN MANIFOLD

365

(Figueiredo and Jain, 2002) it is used. See Figure 2-c

and section 3.3. (4) Knowing the clusters and their

locations, it is required to select the best cluster, ∆x

†

section 3.4. The selection is based on the cluster that

will be more consistent with the PDM (Figure 2-d).

(5) Finally, establish the landmark matching score as-

signing weights to the foundsolution (section 3.5) and

performing global PDM optimization (section 3.1).

2 4 6 8 10 12 14 16 18 20

370

375

380

385

390

190

195

200

205

210

215

0.5

1.5

2.5

2 4 6 8 10 12 14 16 18 20

250

255

260

265

270

275

225

230

235

240

245

0.5

1.5

2.5

2 4 6 8 10 12 14 16 18 20

220

225

230

235

240

245

290

295

300

305

310

315

0.5

1.5

2.5

2 4 6 8 10 12 14 16 18 20

(a)

315

320

325

330

335

340

390

395

400

405

410

(b) (c) (d) (e)

Figure 2: Overview of the DAAM-R. The left main ﬁgure

represents the ﬁrst iteration of the method. Starting with an

initial estimate of the position of the face (by AdaBoost).

a) Response maps of covariance of features dissimilarity

around each x

(blue small dissimilarity). b) 3D mesh for

the response maps. At the ground level with red color is

represented the mean-shift seeds starting grid. The green

circles are the seeds ﬁnal position (local minima). c) Unsu-

pervised clustering to ﬁnd the clusters and their locations.

The red cross at the center represents the current landmark

position x

. The small green circles are the mean-shift seeds

at a near local minima location and the ellipses are the clus-

ters found. d) Representation for Σ

. e) Detailed matching

solutions. The green dots are the centroid locations, x

∗

and the selected solution x

†

is the one pointed by the green

arrow.

3.1 Global Optimization - Fitting the

PDM

The PDM ﬁtting is accomplish using the Lucas and

Kanade framework(Baker and Matthews, 2004). The

warp function is given by

W(x, p, q) = s

+ Φp+ Ψq (3)

where p is the shape parameters and q the similarity

parameters. The non-rigid alignment can be posed

into the following optimization problem

argmin

p,q

∑

k=1

ρ(C

+ Φp+ Ψq}), C

∗

) (4)

minimizing the covariance dissimilarity ρ(.) between

the model covariance, C

∗

, and the covariance com-

puted on a shifted location, but constrained to be con-

sisted with the PDM, C

+ Φp+ Ψq}), for all the

v patches in the model. The model covariance, C

∗

starts by being the average C

on the Manifold. Is

computed from the training images and is weighted

updated every frame enforcing the temporal appear-

ance consistency using the approach described in sec-

tion 2.2.2. A T sized buffer is used to evaluate C

∗

This update process is only done after the PDM ﬁtting

of the target frame. For solving the cost function eq.

4, a weighted least-squares optimization, proposed by

(Wang et al., 2008a), is used. It requires ﬁnding v

local translations by exhaustively search the region

around each patch such that

∆x

†

= argmin

∆x

ρ(C

+ ∆x

}), C

∗

) (5)

where ∆x

†

is the optimal, in some sense, local dis-

placement for the patch k. The evaluation of ∆x

†

described on the following subsections. The weighted

least-squares warp update is given by

∆p =

∂W(x, p, q)

∂p

∂W(x, p, q)

∂p

−1

∂W(x, p, q)

∂p

W∆x

†

(6)

where the Jacobian of the warp is given by

∂W(x,p,q)

∂p

= Φ

and

∂W(x,p,q)

∂q

= Ψ

. W is

a 2v × 2v diagonal matrix of weights, W =

diag(w

, ..., w

, w

, ..., w

). Each w

weight, measures

the ﬁtting importance for landmark k. See section 3.5

for details in how to estimate the weights. The pa-

rameters update equation for ∆q is similar to eq.6 but

insted of using

∂W(x,p,q)

∂p

it uses

∂W(x,p,q)

∂q

. For this

particular case the Jacobian of the warp is constant,

and the forward additive update method(Baker and

Matthews, 2004) can be used. Solving the PDM con-

sists in iteratively use eq.6 and update the parameters

by p ← p+ ∆p and q ← q + ∆q until k∆pk ≤ ε, or a

maximum number of iterations is reached. Note that

the image normalization process, described earlyer in

section 2.3, is performed at each iteration.

3.2 Weighted Mean-Shift - Find

Candidates

Mean-shift algorithm is a robust clustering technique

which does not require prior knowledge on the num-

ber of clusters(Comaniciu and Meer, 2002). The

weighted mean shift vector at point x is deﬁned

as m

(x) =

∑

i=1





x−x





∑

i=1





x−x





where g(s) = −k

′

(s),

with k(s) being the kernel proﬁle (it is used k(s) =

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

366

−

) and the h bandwidth. w

is the normalized

weight assigned to each data point x

. The algo-

rithm starts at the data points and at each iteration

t moves in the direction of the mean shift vector

t+1

= x

+ m

). The mean-shift vector always

points toward the direction of the maximum increase

in the density. If weights are assigned as w

i,i=1,...,m

−1

+ ∆x

}, C

∗

), where m is the number of

seeds (i.e. equal to the inverse of the dissimilarity

of the response maps), the seeds will move into the

local minima. Note that the weights, w

, should be

normalized such that

∑

i=1

= 1. The selection of

the number and the starting position of the seeds is

very important. A sparse grid of 3× 3 blocks is used,

where a single seed is assigned to the position inside

the block that has the higher weight. The number of

seeds used, m, will be the number of 3× 3 blocks in-

side the grid of the scanned areas.

3.3 Finding Clusters

The mean-shift will provide candidates to solutions.

Searching for those candidates is a clustering prob-

lem. For this propose the unsupervised clustering

method proposed by (Figueiredo and Jain, 2002) was

used. Usually the mean-shift seeds converge around

a few locations, forming clusters where the seeds are

not positioned at the exact same place. The clustering

also ﬁlters this effect by taking the centroid position

as the candidate solution.

3.4 Selecting the Best Cluster

Knowing the clusters and their centroid locations it

is required to select the best cluster. The selection

is based on the cluster that is more consistent with

the PDM. Recalling Figure 1-c, the individual shape

localization covariance, Σ

, was estimated. The se-

lected cluster is the one that has the lower maha-

lanobis distance w.r.t. the correspondent PDM land-

mark. Formally, the centroid locations x

∗

are given

by x

∗

= x

+ ∆x

∗

with i = 1, . . . , c, and c the num-

ber of centroids found. The deviation update found

for each cluster is ∆x

∗

. The selected candidate for

the solution, x

†

, is the one that has the lower maha-

lanobis distance, i.e. is more close to the PDM dis-

tribution x

†

= argmind

∗

, Σ

), where d

(.) is the

mahalanobis distance that is evaluated for all x

∗

, and

is the shape position covariance of the landmark k.

3.5 Landmark Matching Score

The PDM optimization is based on a weighted least-

square warp update, dealing with some possible land-

marks mismatches. From eq.6 this information is

included as a diagonal matrix of weights and those

weights are based on landmark conﬁdences. The

statistics for the landmarks covariance of features

matching score can be learnt previously from the

training images. The residual error on matching, C

follows a half normal which is approximated by a

normal distribution with zero mean and a given stan-

dard deviation ∼ N (0, σ

). The error standard de-

viation σ

can be estimated from the training set

as σ

∑

i=1

ρ(C

)

N−1

, where N is the total num-

ber of images. Knowing σ

and deﬁning C

†

to be

the covariance of features evaluated at the solution

†

, the weights for the matrix W can be assigned as

= exp



−

ρ(C

†

∗

)

2σ



4 EXPERIMENTAL RESULTS

The experimental results were conducted using two

free available independent datasets. The IMM

dataset

annotated with v = 58 landmarks, see Fig-

ure 1-a and the FGNet Talking Face sequence (TF).

The main experience consists on training the DAAM-

R with about 160 near frontal images from the IMM

set and test the ability of ﬁtting in unseen images,

comparing it with other ﬁtting algorithms trained with

the same input data. The DAAM-R training consists

in building the PDM, compute the average covariance

of features for each landmark, C

, and ﬁnd the match-

ing statistics σ

using only the images from the IMM

set. The ﬁtting accuracy is evaluated using the ini-

tial 1000 frames of the TF sequence. Our method

(DAAM-R) is compared with the standard AAM al-

gorithms: the Project Out (PO)(Matthews and Baker,

2004), the Simultaneous Inverse Compositional (SIC)

and the SIC Efﬁcient Approximation (SIC-EA)(Baker

et al., 2003). The method is also tested against the

robust extensions: Roboust Normalization Inverse

Compositional (RNIC)(Baker et al., 2003) and the

Roboust SIC (RSIC)(Baker et al., 2003). Regarding

the remaining details about the DAAM-R, the sam-

pled patches P

have the size of 11 × 11, (l = 11),

(intraocular distance of about 80 pixels). Durring the

ﬁtting process the search area is a window of 21× 21

pixels around each landmark. For the mean-shift,

www2.imm.dtu.dk/ aam

TOWARDS GENERIC FITTING USING DISCRIMINATIVE ACTIVE APPEARANCE MODELS EMBEDDED ON A

RIEMANNIAN MANIFOLD

367

the system works well with a bandwidth of h = 8,

ε = 0.01, and maximum number of iterations 50. The

number of seeds used were m = 49. The unsupervised

clustering requires the minimal and maximal number

of clusters to ﬁnd, 1 and 5 respectively. The model

covariance buffer is T = 30, which means that that

for every landmark the C

∗

is computed from 30 pre-

vious weighted samples. The termination criteria in

DAAM-R was set to ε = 0.75 and the maximum iter-

ations was set to 10. For the other algorithms ε = 0.75

and maximum iterations of 20. The robust algorithms

also require the choose of a error norm, the Talwar

function is used (gives a weight of 1 to inliers and 0 to

outliers), where the scale parameter is estimated from

the error image assuming that there exists 15% of out-

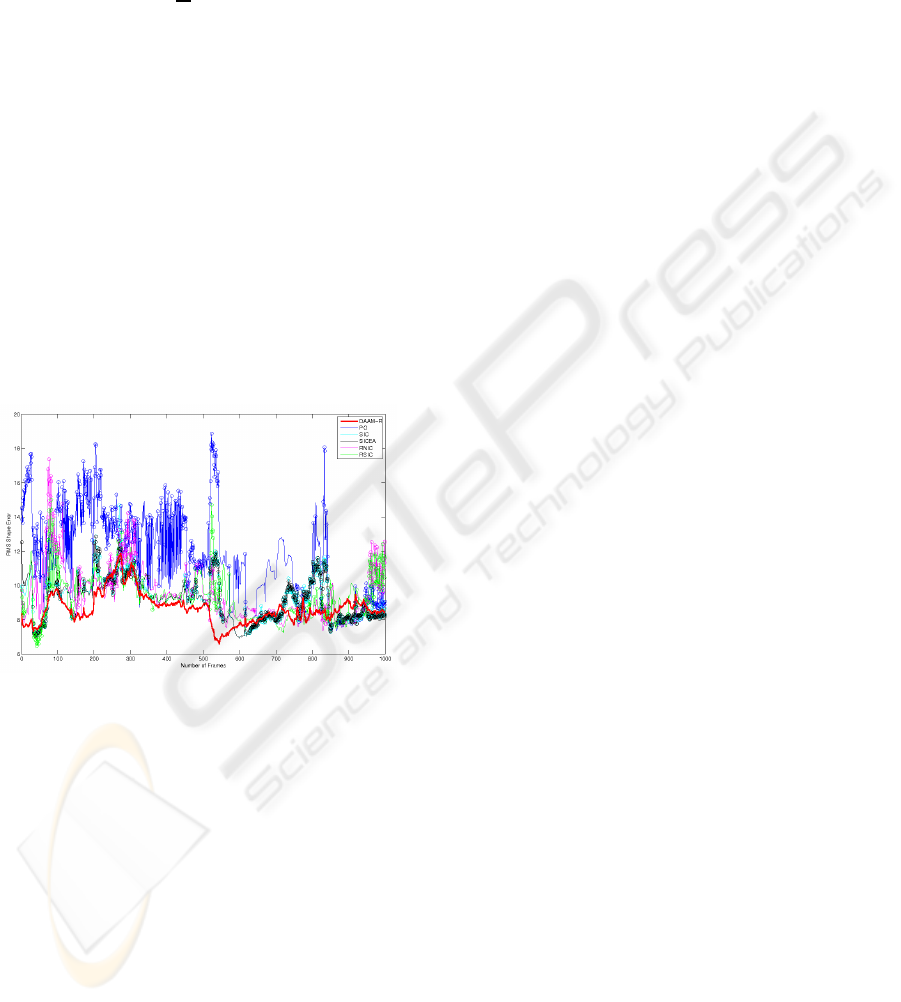
liers. The Figure 3 shows the RMS ﬁtting error in the

TF sequence for all the evaluated methods. Since the

IMM uses a 58 landmark scheme and the TF uses 68,

the error was only measured over the correspondent

landmarks. The colored circles over the graphic rep-

resent reinitializations of the models. Note that our

approach, DAAM-R, never make a restart. The re-

sults show that the method is generally very accurate.

Figure 3: Top ﬁgures are the ﬁtted frames 1 and 500 of the

Talking Face sequence for every algorithms. At bottom the

RMS error in ﬁtting the ﬁrst 1000 frames of the Talking

Face video sequence (unseen data). Best viewed in color.

5 CONCLUSIONS

The DAAM-R uses independent shape and texture

models. The texture is composed by a set descriptors

for the landmarks. These descriptors are covariances

of multiple features evaluated around the landmark

locations which is governed by a PDM. The covari-

ance matrices lie on a Riemannian manifold, which

make possible to measure the dissimilarity and to up-

date them, imposing the temporal appearance consis-

tency. Using a discriminative fashion ﬁtting approach,

response maps are found. Since the minimum of the

responce map isn’t always the correct solution a strat-

egy based on mean-shift is used to ﬁnd candidates to

solutions (local minima). An unsupervised cluster-

ing technique is used to locate and group the candi-

dates and a mahalanobis based metric is used to se-

lect the best solution consistent with the PDM. The

global optimization for the PDM is performed using

a weighted least-squares warp update, where weights

were extracted from the landmark matching conﬁ-

dences statistics. The DAAM-R trained with mostly

frontal images taken from the IMM dataset is evalu-

ated by ﬁtting to unseen data on the challenging Talk-

ing Face video sequence (1000 frames). The model

performs well without lose track during all the se-

quence. As future work we propose to used the mean-

shift using an adaptive bandwith, improving the so-

lution section and a evaluation for the quality of the

selected vector of features. As a ﬁnal note, the en-

tire process can be speeded up using the integral im-

age covariance computation and is suitable for paral-

lel computing since the response patches for the land-

marks are independent.

REFERENCES

Baker, S. and Matthews, I. (2004). Lucas-kanade 20 years

on: A unifying framework. International Journal of

Computer Vision, 56(1):221 – 255.

Baker, S., R.Gross, and I.Matthews (2003). Lucas kanade

20 years on: A unifying framework: Part 3. Technical

report, CMU Robotics Institute.

Batur, A. and Hayes, M. (2005). Adaptive active appearance

models. IEEE Transactions on Image Processing.

Comaniciu, D. and Meer, P. (2002). Mean shift: A robust

approach toward feature space analysis. IEEE PAMI.

D.Cristinacce and T.F.Cootes (2008). Automatic feature

localisation with constrained local models. Pattern

Recognition.

Figueiredo, M. A. and Jain, A. K. (2002). Unsupervised

learning of ﬁnite mixture models. IEEE PAMI.

Gross, R., Matthews, I., and Baker, S. (2005). Generic vs.

person speciﬁc active appearance models. Image and

Vision Computing, 23(1):1080–1093.

Matthews, I. and Baker, S. (2004). Active appearance mod-

els revisited. IJCV.

Matthews, I., Ishikawa, T., and Baker, S. (2004). The tem-

plate update problem. IEEE Transactions on Pattern

Analysis and Machine Intelligence, 26(1):810 – 815.

Pennec, X., Fillard, P., and Ayache, N. (2006). A rieman-

nian framework for tensor computing. IJCV.

Porikli, F., Tuzel, O., and Meer, P. (2006). Covariance track-

ing using model update based on lie algebra. In IEEE

CVPR.

Sung, J. and Kim, D. (2009). Adaptive active appearance

model with incremental learning. Pattern Recognition

Letters.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

368

T.F.Cootes, Edwards, G., and C.J.Taylor (2001). Active ap-

pearance models. IEEE PAMI.

Wang, Y., Lucey, S., and Cohn, J. (2008a). Enforcing con-

vexity for improved alignment with constrained local

models. In IEEE CVPR.

Wang, Y., Lucey, S., Cohn, J., and Saragih, J. M. (2008b).

Non-rigid face tracking with local appearance consis-

tency constraint. In IEEE Automatic Face and Gesture

Recognition.

TOWARDS GENERIC FITTING USING DISCRIMINATIVE ACTIVE APPEARANCE MODELS EMBEDDED ON A

RIEMANNIAN MANIFOLD

369