A GEOMETRIC APPROACH TO CURVATURE ESTIMATION ON

TRIANGULATED 3D SHAPES

Mohammed Mostefa Mesmoudi, Leila De Floriani and Paola Magillo

Department of Computer Science and Information Science (DISI), University of Genova

Via Dodecaneso 35, 16146 Genova, Italy

Keywords:

Gaussian and mean curvatures, Surface meshes.

Abstract:

We present a geometric approach to deﬁne discrete normal, principal, Gaussian and mean curvatures, that

we call Ccurvature. Our approach is based on the notion of concentrated curvature of a polygonal line and

a simulation of rotation of the normal plane of the surface at a point. The advantages of our approach is its

simplicity and its natural meaning. A comparison with widely-used discrete methods is presented.

1 INTRODUCTION

Curvature is one of the main important notions used

to study the geometry and the topology of a surface.

In combinatorial geometry, many attempts to deﬁne a

discrete equivalent of Gaussian and mean curvatures

have been developed for polyhedral surfaces (Gatzke

and Grimm, 2006; Surazhsky et al., 2003). Dis-

crete approaches include smooth approximations of

the surface using interpolation techniques (Hahmann

et al., 2007), and approaches that deal directly with

the mesh (Meyer et al., 2003; Taubin, 1995; Watanabe

and Belyaev, 2001). All the methods are not satisfac-

tory in what concerns approximation errors, control,

and convergence when reﬁning a mesh (Borrelli et al.,

2003; Surazhsky et al., 2003; Xu, 2006).

In the ﬁfties, Aleksandrov introduced concen-

trated curvature as an intrinsic curvature measure for

polygonal surfaces (Aleksandrov, 1957). This tech-

nique has been used in the geometric modeling com-

munity under the name of angle defect method (Al-

boul et al., 2005; Akleman and Chen, 2006). Con-

centrated curvature does not suffer from the problems

linked to errors and and their control, and satisﬁes a

discrete analogous version of the well known Gauss-

Bonnet theorem. However, Concentrated curvature

depends weakly on the local geometric shape of the

surface.

Here, we use Aleksandrov’s idea to deﬁne con-

centrated curvature for polygonal lines. We prove in

such a case that concentrated curvature is an intrin-

sic measure that is expressed using only the fracture

angle of the polygonal line at its vertices. We then

deﬁne a discrete normal curvature of a polygonal sur-

face at a vertex. We simulate the rotation of normal

planes to deﬁne principal curvatures and, thus, obtain

new discrete estimators for Gaussian and mean curva-

tures. We call all such curvatures Ccurvatures, since

they are obtained as generalization to surfaces of the

concept of concentrated curvature for polygonal lines

just introduced. The major advantage of this method

is the use of intrinsic properties of a discrete mesh to

deﬁne geometric features that have the same proper-

ties as the analytic methods. In this work, we also

compare Gaussian and mean Ccurvatures with widely

used discrete curvature estimators for analytic Gaus-

sian and mean curvatures and with concentrated cur-

vature (according to Aleksandrov’s deﬁnition).

2 BACKGROUND NOTIONS

In this Section, we brieﬂy review some fundamental

notions on curvature in the analytic case and on con-

centrated curvature.

Let C be a smooth curve having parametric repre-

sentation (c(t))

t∈R

. The curvature k(p) of C at a point

p = c(t

) is given by

k(p) =

(t) ∧ c”(t)|

(t)|

where ρ is called the curvature radius. Number ρ cor-

responds to the radius of the osculatory circle tangent

to C at p.

Mesmoudi M., De Floriani L. and Magillo P. (2010).

A GEOMETRIC APPROACH TO CURVATURE ESTIMATION ON TRIANGULATED 3D SHAPES.

In Proceedings of the International Conference on Computer Graphics Theory and Applications, pages 90-95

DOI: 10.5220/0002825900900095

 SciTePress

Let S be a smooth surface and Π be a plane which

contains the unit normal vector

−→

at a point p ∈ S.

Plane Π intersects S through a smooth curve C con-

taining p with curvature k

(p) at the point p called

normal curvature. When Π turns around

−→

, curves

C vary. There are two extremal curvature values

(p) ≤ k

(p) which bound the curvature values of

all curves C. The corresponding curves C

and C

are orthogonal at point p (Do Carno, 1976). These

extremal curvatures are called principal normal cur-

vatures. Note that, if the normal vector

−→

is on the

same side as the osculatory circle, then the curvature

value k

of curve C

has a negative sign.

Deﬁnition 1. The Gaussian curvature K

and the

mean curvature H

at point p = φ(x, y) are deﬁned,

respectively, as

= k

(p) ∗ k

(p), H

(p) + k

(p)

(1)

The formula deﬁning H

turns out to be the mean

of all values of normal curvatures at point p. Gaus-

sian and mean curvatures depend strongly on the (lo-

cal) geometrical shape of the surface. We will see that

this property is relaxed for concentrated curvature. A

remarkable property of Gaussian curvature is given

by the Gauss-Bonnet Theorem, which relates the ge-

ometry of a surface, given by the Gaussian curvature,

to its topology, given by its Euler characteristic (see

(Do Carno, 1976)).

A singular ﬂat surface is a surface endowed with a

metric such that each point of the surface has a neigh-

borhood which is either isometric to a Euclidean disc

or a cone of angle Θ 6= 2π at its apex. Points satis-

fying this latter property are called singular conical

points. Any piecewise linear triangulated surface has

a structure of a singular ﬂat surface. All vertices with

a total angle different from 2π (or π for boundary ver-

tices) are singular conical points. As shown below,

the Gaussian curvature is accumulated at these points

so that the Gauss-Bonnet formula holds.

Let Σ be a (piecewise linear) triangulated sur-

face and let p be a vertex of the triangle mesh. Let

∆

,· ·· ,∆

be the triangles incident at p such that ∆

and ∆

i+1

are edge-adjacent. If a

, b

are the vertices

of triangle ∆

different from p, then the total angle Θ

at p is given by Θ

∑

i=1

[

Deﬁnition 2. (Aleksandrov, 1957; Troyanov, 1986)

The concentrated Gaussian curvature K

(p), at a

vertex p of the triangulated surface, is the value

(p) =



2π − Θ

if p is an interior vertex, and

π − Θ

if p is a boundary vertex.

The above discrete deﬁnition of curvature can be

justiﬁed as follows. The surface is assumed to have

a conical shape at each of its vertices. Each cone is

then approximated from its interior with a sphere S

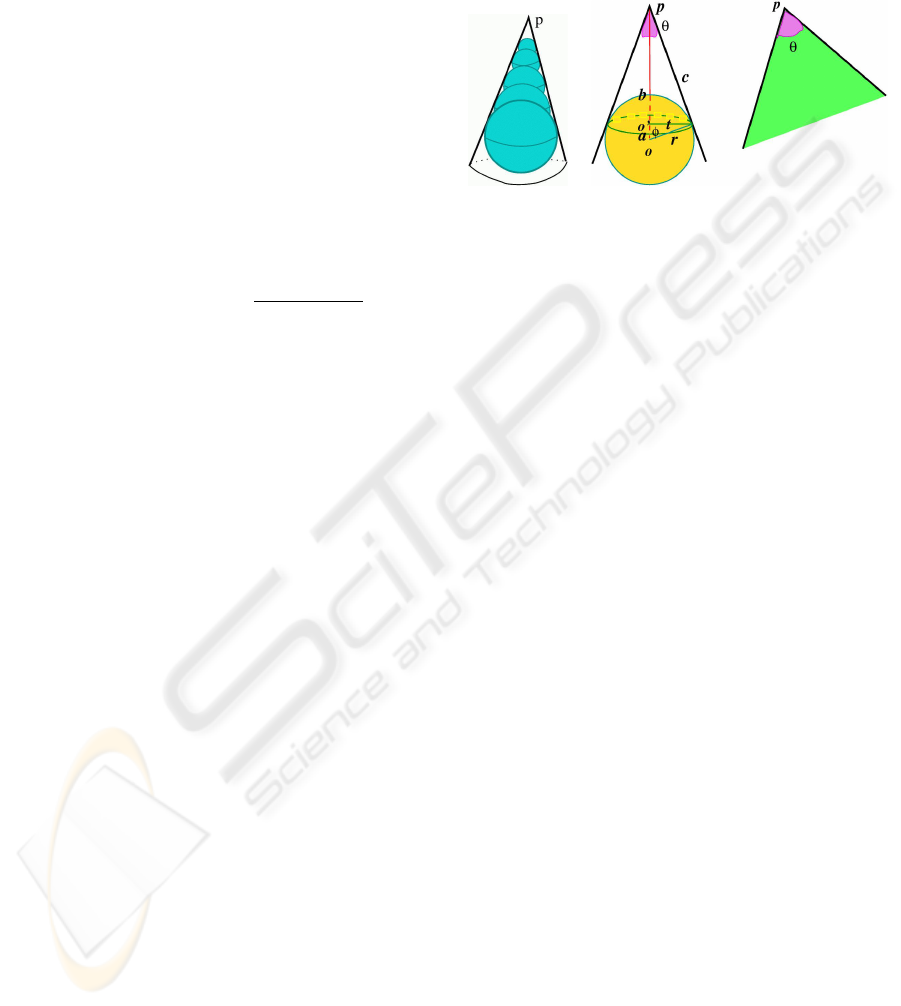
of radius r, as shown in Figure 1(a). Following

(a) (b)

Figure 1: In (a), spheres tangent to a cone from it interior;

in (b), parameters for computation.

the Gauss-Bonnet theorem, the spherical cap approx-

imating the cone has a total curvature which is equal

to 2π−Θ, where Θ is the angle of the cone at its apex.

This quantity does not depend on the radius of sphere

by which we approach the cone and hence 2π −Θ

is an intrinsic value for the surface at vertex p. This

remarkable property fully justiﬁes the name concen-

trated curvature.

The local shape of the surface does not play a

role here, unlike in the analytic case, where Gaus-

sian curvature is strongly dependent of the local sur-

face shape. Concentrated curvature satisﬁes a discrete

equivalent of the Gauss-Bonnet theorem (Akleman

and Chen, 2006).

3 CCURVATURE FOR

POLYGONAL CURVES

In this Section, we use the concentrated curvature

principle to deﬁne a concentrated curvature for polyg-

onal curves. In this way, we can deﬁne principal con-

centrated curvatures for a triangulated surface and fol-

low the same construction, used in Section 2 for an-

alytic mean and Gaussian curvatures, to deﬁne simi-

larly new discrete curvature estimators. We will call

them Ccurvatures. The initial C is a shortcut for “con-

centrated”. We will show also that Ccurvature does

not suffer from convergence problems.

Let C be a simple polygonal curve in the three-

dimensional Euclidean space. Let p be a vertex on C

and a, b its two neighbors on C. Points a, b and p

deﬁne a plane Π. If the angle γ =

apb is equal to π,

then the curvature value k(p) of C is 0. Otherwise, let

⊂ Π be a circle of any radius r > 0 tangent C at two

A GEOMETRIC APPROACH TO CURVATURE ESTIMATION ON TRIANGULATED 3D SHAPES

points u ∈ [p, a] and v ∈ [p, b] (see Figure 2(a)).

(a) (b)

Figure 2: In (a), circles tangent to the sector from it interior.

In (b), computing total curvature of arc (uv).

Let (uv) be the arc of S

delimited by u and v and

located in triangle ∆(upv). Then, the polygonal path

apb can be smoothly approximated by the path [au]∪

(uv) ∪ [vb] for any value of r (see Figure 2(a)). The

curvature value at any point of circle S

is constant

and equal to 1/r. Let O be the center of S

and θ be

the angle

uOp =

vOp. The total curvature of (uv) is

given by:

k =

(uv)

dl =

l(uv) =

2rθ = π − γ. (2)

The above quantity does not depend on the radius of

circle S

through which we approximate the curve.

This means that π − γ is an intrinsic quantity of curve

C at vertex p since it depends only on the fracture an-

gle γ. Then, we can give the following deﬁnition:

Deﬁnition 3. Concentrated curvature of C at p is the

total curvature π −γ of arcs (uv) approximating curve

C around point p. We simply call it Ccurvature and

we denote it by k

(p).

Let C be a discrete piecewise-linear oriented pla-

nar curve. Suppose that C is parameterized, and hence

oriented, by its natural arc length s and that the posi-

tive angle orientation is counterclockwise. At a vertex

of the curve for which the next segment is not aligned

with the previous one, the deviation angle γ at the ver-

tex is computed in the positive sense from the pre-

vious segment to the new segment. With this con-

vention the Ccurvature π − γ of a parameterized curve

may have negative or positive values.

4 CCURVATURE FOR

TRIANGULATED 3D SURFACES

Let Σ be a piecewise linear triangulated surface and

p be a vertex of Σ. Let

−→

n be the normal vector at p

deﬁned by the average of the normal vectors of the

triangles incident in p. Let Π be a plane passing by p

and containing the normal vector

−→

n . This plane cuts

surface Σ along a polygonal curve C = Σ ∩ Π con-

taining point p. We compute the Ccurvature k

(p) at

point p of curve C as described in Section 3. Note

that the position of the normal vector

−→

n with respect

to the polygonal curve C should be taken into account.

If the normal vector

−→

n and the polygonal curve C

lie in two different half planes (or equivalently they

are separated by the “tangent” plane T

whose normal

vector is

−→

n , see Figure 3), then the angle γ of C at

p is smaller than π and the Ccurvature value π − γ is

positive. Otherwise, the angle γ of C at p is larger

than π and the Ccurvature value π − γ is negative. In

this case, for simplicity of computation, we observe

that if γ

is the geometric angle of C at p (i.e., γ

is the

supplementary angle of γ: γ + γ

= 2π), then we have

π − γ = γ

− π. This Ccurvature value corresponds to

the normal curvature at vertex p.

Figure 3: Intersection of plane Π with a smooth surface.

Angle at p is divided into two equal angles.

When plane Π turns around

−→

n , we obtain a set of

Ccurvature values bounded (respectively from below

and from above) by two extremal values k

C,1

(p) ≤

C,2

(p) . Values k

C,1

(p) and k

C,2

(p) correspond to the

principal curvatures. Based on them, we can deﬁne

a mean and a Gaussian curvature, in a similar way as

we do in the analytic case:

Deﬁnition 4. The extremal values k

C,1

(p) and k

C,2

(p)

bounding the set of k

(p)’s are called the principal

Ccurvatures at vertex p.

Deﬁnition 5. The Gaussian Ccurvature K

(p) of Σ

at vertex p is deﬁned as the product k

C,1

(p) ∗ k

C,2

(p).

Deﬁnition 6. The mean Ccurvature H

(p) of surface

Σ at vertex p is deﬁned as the mean value of all nor-

mal Ccurvature values obtained by turning plane Π

around the normal vector.

Note that all these values are intrinsic values de-

pending only on the local geometric shape of surface

Σ.

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

In practice, we cannot compute all the normal

Ccurvature values (k

(p)) since the rotation of plane

Π generates an inﬁnite sequence of values. We can

extract a subsequence for computing an approxima-

tion of principal Ccurvatures.

Following the way in which normal curvature is

deﬁned for smooth surfaces (see Section 2), we simu-

late a discrete rotation around the normal vector

−→

a vertex p of the plane Π containing

−→

, by consider-

ing one plane for each vertex v

in the star of p. Given

, we take the curve where plane Π

, containing p,

−→

and v

, intersects the star of p, and compute its cur-

vature. This process gives a discrete rotation around

p. Each intersection curve is a polygonal line (v

)

where w

is the intersection point between plane Π

and the link of p. The angle γ

= [v

, in the interior

of the cone, between vectors

−→

and

−→

is deﬁned by

:= arccos(

−→

.pw

). The normal Ccurvature at p

of the polygonal line (v

) is deﬁned by ∓(π − γ

The sign +1 or −1 is deﬁned by following the po-

sition of the normal vector

−→

with respect to the

polygonal line (v

) as explained above. Follow-

ing this construction, principal, mean and Gaussian

Ccurvatures can be deﬁned at p.

5 EXPERIMENTAL RESULTS

In this Section, we experimentally compare our

Ccurvatures with other classic approaches to compute

discrete curvatures.

We compare Gaussian Ccurvature with concen-

trated curvature (described in Section 2) and with

Gaussian angle deﬁcit. The Gaussian angle-deﬁcit

curvature estimator (Meyer et al., 2003) is deﬁned at

a vertex p by

(2π − Θ

), (3)

where Θ

is the angle at p formed by the j-th triangle

incident at p, and A is the area of the 1-ring neighbor-

hood around p or the Voronoi region around p.

We compare mean Ccurvature with mean angle

deﬁcit. The mean angle-deﬁcit curvature estimator

(Meyer et al., 2003) is deﬁned, at point p, as the mag-

nitude of the following mean curvature vector nor-

malized by the area of the surrounding (Voronoi or

barycentric) neighborhood:

∑

j=1

(cotα

+ cot β

)(p − x

), (4)

where angles α

and β

correspond to the remaining

summits of the quadrilateral formed by the two trian-

gles adjacent to edge px

. Sign ± is assigned to |H

following the direction of the mean curvature vector

with respect to the normal vector of the surface at

point p.

5.1 Behavior on the Sphere

Mean angle deﬁcit

Mean Ccurvature

Figure 4: Curvature values along a meridian of the sphere,

approximated with a polyhedron made up of 5k (red), 20k

(blue), 80k (green) triangles.

The objective of discrete curvature estimators is

not to produce discrete curvature values close to an-

alytic ones, but to exhibit the same behavior as the

analytic ones, although they may produce curvature

values in their own range. This is sufﬁcient for many

applications (e.g., mesh segmentation at lines of min-

imal curvature).

On a sphere, both Gaussian and mean analytic

curvatures are constant. Since discrete curvature es-

timators are mesh-dependent, we analyze their be-

havior on different triangle meshes approximating the

sphere. If a sphere is approximated by a regular poly-

hedron (e.g., an icosahedron), then all discrete estima-

tors give the same value at all vertices, as expected.

Another way to approximate a sphere is drawing a

number of tracks and sectors and triangulating the re-

sulting net (the resolution is controlled by varying the

number of tracks and sectors). Here, not all trian-

gles and angles are equal, and thus the discrete es-

timators give variable results. We performed our tests

with triangle meshes at increasing resolutions. Fig-

A GEOMETRIC APPROACH TO CURVATURE ESTIMATION ON TRIANGULATED 3D SHAPES

Gaussian Ccurvature

Concentrated curvature

Gaussian angle deﬁcit

Mean Ccurvature

Mean angle deﬁcit

Figure 5: The various curvatures on the Camel and the

Retinal meshes, in color scale.

ure 4 shows the curvature values along a meridian

of the sphere, at various resolutions, for mean angle

deﬁcit and mean Ccurvature. Gaussian Ccurvature

and concentrated curvature are very close, and sim-

ilar to mean Ccurvature. Gaussian curvature behaves

in a similar way as mean angle deﬁcit. All estimators

are affected by the different shape and size of trian-

gles at the various latitudes, and give abnormal values

at poles. Unlike all others, the two angle deﬁcit mea-

sures provide higher values near the poles than near

the equator of the sphere. Angle deﬁcit estimators

show a relevant noise, which becomes worse while

increasing resolution, because of the division by area.

The values of other measures vary smoothly along

latitude, and tend to be closer to a constant value at

higher resolutions.

5.2 Comparisons on Discrete 3D Shapes

We compare the curvature estimators on triangulated

shapes of different kinds from the AIM@SHAPE

repository (http://shapes.aim-at-shape.net/). The

Camel mesh has 9770 vertices and 19536 triangles;

the Retinal molecule mesh has 3643 vertices and 7282

triangles. Curvature values are plotted in a color scale

in Figure 5. The color scale is from blue (minimum

negative value) through white (zero) to red (maximum

positive value), where the minimum and maximum

values may be different in the speciﬁc curvature esti-

mators.

Gaussian Ccurvature and concentrated curvature

have a very similar behavior. The two angle deﬁcit

measures tend to give near-zero values (white) to

wider areas, while the other estimators better follow

the geometrical shape of the surface. This is espe-

cially evident on Camel mesh. On Retinal molecule,

all mean estimators and all Gaussian estimators be-

have similarly. The mean and Gaussian Ccurvature

values seem to provide a slightly better delimitation

of positive and negative curvature areas.

In estimating Ccurvatures, we approximate the

continuous rotation of the plane around the surface

normal at a vertex p, in a discrete way, by using just

the planes passing through the neighbors of p. To

get more precision, we may reﬁne the link (i.e., the

boundary of the star) of p by adding new points on

its edges, and consider a plane through each of them.

Experiments show the resulting (mean and Gaussian)

Ccurvature values are almost the same, and this con-

ﬁrm the validity of the approach.

To illustrate the application of curvature to 3D

shape segmentation, we show in Figure 6 two seg-

mentations based on mean Ccurvature, which high-

light convex features.

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

Figure 6: Segmentations of 3D shapes based on mean

Ccurvature.

6 CONCLUDING REMARKS

We have presented a geometrical technique to esti-

mate discretely normal, principal, mean and Gaus-

sian curvatures on a triangulated piecewise linear sur-

face. Our technique describes well the local geo-

metric shape of the surface. The experimental re-

sults we presented validate the approach and show

that Ccurvature behaves better than some mostly used

techniques.

It would be interesting to further investigate the

stability, or convergence of Ccurvature values to some

intrinsic value, when adding more points to reﬁne the

discrete rotation of the cutting plane around a vertex

normal.

Concentrated curvature of polygonal curves has

interesting applications for spatial curves to charac-

terize them via an additional discrete torsion notion,

this will leads to interesting applications in GPS ﬁeld

and robotics (3D motion for example).

The principle of concentrated curvature has also

been used to deﬁne discrete estimators for scalar cur-

vature of 3-combinatorial manifolds.

ACKNOWLEDGEMENTS

This work has been partially supported by the Na-

tional Science Foundation under grant CCF-0541032.

REFERENCES

Akleman, E. and Chen, J. (2006). Practical polygonal mesh

modeling with discrete gaussian-bonnet theorem. In

Proceedings of Geometry, Modeling and Processing.

Alboul, L., Echeverria, G., and Rodrigues, M. A. (2005).

Discrete curvatures and gauss maps for polyhedral

surfaces. In Workshop on Computational Geometry.

the Netherlands.

Aleksandrov, P. (1957). Topologia combinatoria. Torino.

Borrelli, V., Cazals, F., and Morvan, J.-M. (2003). On

the angular defect of triangulations and the pointwise

approximation of curvatures. Comput. Aided Geom.

Des., 20(6):319–341.

Do Carno, M. P. (1976). Differential Geometry of Curves

and Surfaces. Prentice-Hall, Inc.

Doss-Bachelet, C., Franc¸oise, J.-P., and Piquet, C. (2000).

eom

etrie diff

erentielle. Ellipses.

Gatzke, T. and Grimm, C. (2006). Estimating curvature

on triangular meshes. International Journal of Shape

Modeling, 12(1):1–29.

Hahmann, S., Belyaev, A., Bus

e, L., Elber, G., Mourrain,

B., and Roessl, C. (2007). Shape Interrogation. In

Shape Analysis and Structuring, Mathematics and Vi-

sualization, pages 1–57. Springer.

Meyer, M., Desbrun, M., Schr

oder, P., and Barr, A. H.

(2003). Discrete differential-geometry operators for

triangulated 2-manifolds. In Visualization and Mathe-

matics III, pages 35–57. Springer-Verlag, Heidelberg.

Surazhsky, T., Magid, E., Soldea, O., Elber, G., and Rivlin,

E. (2003). A comparison of gaussian and mean cur-

vatures estimation methods on triangular meshes. In

Proceedings of Conference on Robotics and Automa-

tion, 2003., pages 739–743.

Taubin, G. (1995). Estimating the tensor of curvature of

a surface from a polyhedral approximation. In ICCV

’95: Proceedings of the Fifth International Confer-

ence on Computer Vision, page 902.

Troyanov, M. (1986). Les surfaces euclidiennes singularits

coniques. Enseign. Math. (2), 32:79–94.

Watanabe, K. and Belyaev, A. G. (2001). Detection of

salient curvature features on polygonal surfaces. Com-

put. Graph. Forum, 20(3):385–392.

Xu, G. (2006). Convergence analysis of a discretization

scheme for gaussian curvature over triangular sur-

faces. Comput. Aided Geom. Des., 23(2):193–207.

A GEOMETRIC APPROACH TO CURVATURE ESTIMATION ON TRIANGULATED 3D SHAPES