
GPU OPTIMIZER: A 3D RECONSTRUCTION ON THE GPU USING
MONTE CARLO SIMULATIONS
How to Get Real Time without Sacrificing Precision
Jairo R. S
´
anchez, Hugo
´
Alvarez and Diego Borro
CEIT and Tecnun (University of Navarra) Manuel de Lardiz
´
abal 15, 20018 San Sebasti
´
an, Spain
Keywords:
3D reconstruction, Structure from motion, SLAM, GPGPU.
Abstract:
The reconstruction of a 3D map is the key point of any SLAM algorithm. Traditionally these maps are built
using non-linear minimization techniques, which need a lot of computational resources. In this paper we
present a highly paralellizable stochastic approach that fits very well on the graphics hardware. It can achieve
the same precision as non-linear optimization methods without loosing the real time performance. Results are
compared against the well known Levenberg-Marquardt algorithm using real video sequences.
1 INTRODUCTION
Real time simultaneous localisation and mapping
(SLAM) consists of calculating both the camera
motion and the 3D reconstruction of the observed
scene at the same time. This work addresses the 3D
reconstruction problem, i.e., obtaining a set of 3D
points that represents the observed scene using only
the information provided by a single camera.
If the required precision is high, existing re-
construction algorithms are usually very slow and
not suitable for real time operation. This work
proposes an implementation that can achieve a high
level of accuracy in real time, taking advantage of the
graphics hardware available in any desktop computer.
This work develops a new 3D reconstruction algo-
rithm based on Monte Carlo simulations that can be
directly executed on a modern GPU. The algorithm
consists of approximating the maximum likelihood
estimator, random sampling from the space of pos-
sible locations of the 3D points. Since each sample
is independent from others, this method exploits well
the data level parallelism required by this program-
ming model.
For validating it, we have compared both preci-
sion and performance with the implementation of the
Levenberg-Marquardt non-linear minimization algo-
rithm given in (Lourakis, 2004).
2 PROBLEM DESCRIPTION
It is assumed that there is an image source that feeds
the algorithm with a constant flow of images. Let
I
k
be the image of the frame k. Each image has a
set of features associated to it given by a 2D feature
tracker Y
k
=
~y
k
1
,...,~y
k
n
. Feature ~y
k
i
has
u
k
i
,v
k
i
coordinates. The 3D motion tracker calculates the
camera motion for each frame as a rotation matrix and
a translation vector x
k
=
R
k
|
~
t
k
, where the set of all
computed cameras up to frame t is X
t
=
{
x
1
,...,x
t
}
.
The problem consists of estimating a set of 3D points
Z
t
=
{
~z
1
,...,~z
n
}
that satisfies the following equation:
~y
k
i
= Π
R
k
~z
i
+
~
t
k
∀i ≤ n, ∀k ≤ t (1)
where Π is the pinhole projection function. For
simplicity, the calibration matrix can be obviated in
Equation 1 if 2D feature points are represented in
normalized coordinates instead of pixel coordinates.
2.1 Proposed Algorithm
A 3D structure optimization method is proposed, that
performs a global minimization using a probabilisti-
cal approach based on the Monte Carlo simulation
paradigm (Metropolis and Ulam, 1949). This ap-
proach consists of generating inputs randomly from
the domain of the problem. These possible solu-
tions are then weighted using some type of function
depending on the measurement obtained from the
system. Monte Carlo simulations are suitable for
443
R. Sánchez J., Álvarez H. and Borro D. (2010).
GPU OPTIMIZER: A 3D RECONSTRUCTION ON THE GPU USING MONTE CARLO SIMULATIONS - How to Get Real Time without Sacrificing
Precision.
In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 443-446
DOI: 10.5220/0002826704430446
Copyright
c
SciTePress

problems were it is not possible to calculate the exact
solution from a deterministic algorithm, i.e., the case
of 3D reconstruction from 2D image features, since
the direct method is ill-conditioned.
However, this strategy leads to very computation-
ally intensive implementations that makes it unusable
for real time operation. One of the key features
of these simulations is that each possible solution
is computed independently from others, making it
optimal for data-streaming architectures, like GPUs.
This system completments the 3D camera tracker
presented in (Eskudero et al., 2009) that also runs on
the GPU using a similar paradigm.
Every new frame, at time t + 1, the set Z
t
is
enlarged with new points and refined with the new
observations Y
t+1
provided by the feature tracker,
getting a new set Z
t+1
. Unlike probabilistic batch
methods, the proposed optimizer uses all the available
frames for doing this optimization, since the GPU can
handle them comfortably. Of course, there is a limit
in the amount of frames that the GPU can process in
real time. The overall view of the proposed method
has the following steps:
1. Initialize New 3D points. The algorithm tries to
triangulate new 3D points using the feature points
provided by the tracker.
2. Generate Samples from Nnoisy 3D Points. The
system generates new hypotheses about the lo-
cation of the 3D points using the available 3D
structure as initial guess.
3. Evaluate the Hypotheses. Hypotheses are evalu-
ated using an objective function that computes the
projection residual of all the samples against all
the available measurements. The best one is used
as new location for the 3D point.
3 GPU IMPLEMENTATION
The algorithm is composed by three shader programs.
These programs will run sequentially for each point to
be optimized. The first shader program will generate
all the hypotheses for a single point location, the sec-
ond shader program will compute the weight of each
hypothesis and the third shader program will choose
the best candidate among the hypotheses. Algorithm
1 shows a general overview of the proposed method.
The parts executed on the GPU have the GPU prefix.
3.1 Data Structures
Since the GPU is a hardware designed to work with
graphics, the way to load data on it, is using image
textures. The output is obtained using the render-to-
texture capabilities of the graphics card. It is very
important to choose good memory structures since
the transfers between the main memory and the GPU
memory are very slow.
In our case, the hypotheses for the location of a 3D
point are stored in a RGBA texture. Each hypothesis
has its coordinates stored in the RGB triplet and
the result of evaluating the objective function in the
alpha channel. Another similar texture is used as
framebuffer. Each texel of these textures will be a
single hypothesis, so the total number of hypotheses
for each point will be the size of the texture squared.
Another RGB texture is used for storing ran-
dom numbers generated in the CPU. This is because
graphics hardware lacks random number generating
functions. This texture is computed in preprocessing
stage and remains constant, converting this method in
a pseudo-stochastic algorithm. Interested readers can
refer to (Eskudero et al., 2009) for more details.
Algorithm 1: Overview of the GPU minimization.
for all~z
i
in Z
t
do
SendToGPU(~z
i
)
GPU SampleHypotheses()
for all ~y
k
i
in
{
Y
1
,...,Y
t
}
do
SendToGPU(~y
k
i
, x
k
)
GPU EvaluateHypotheses()
end for
ˆ
~z
i
= GPU GetBestHypothesis()
Z
t+1
←ReadFromGPU(
ˆ
~z
i
)
end for
3.2 Initialization
New points are initialized via linear triangulation.
This is a very ill-conditioned procedure and its results
are unusable, but it is a computationally cheap starting
point for the minimization algorithm. This stage is
implemented in the CPU since it runs very fast, even
when triangulating many points.
3.3 Sampling Points
In this step all the 3D points in the map are subject
to be optimized. This stage runs when new points are
triangulated and when new frames are tracked. Trian-
gulated points have large error due to ill-conditioned
systems of equations, and existing points can be
improved with the new measures provided by the
feature tracker.
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
444
For each point ~z
i
, a set of random samples S
i
=
n
~z
(1)
i
,...,~z
(m)
i
o
is generated around its neighborhood.
The stochastic sampling function used is a uniform
random walk around the initial point:
~z
(n)
i
= f (~z
i
,~n
i
) =~z
i
+~n
i
, ~n
i
∼ U
3
(−s,s) (2)
where ~n
i
is a 3-dimensional uniform distribution hav-
ing minimum in -s and maximum in s. The parameter
s is chosen to be directly proportional to the prior
reprojection error of the point being sampled. In this
way, the optimization behaves adaptively avoiding
falling into local minimums and handling well points
far from the optimum. The GPU implementation is
performed using a fragment shader. The data needed
are the 3D point to be optimized and the texture
with the random numbers. The output is a texture
containing the coordinates for all hypotheses. The
only datum transfered is the 3D point coordinates,
because the the random numbers are transfered in
preprocessing stage. It is not necessary to download
the generated hypotheses to main memory, because
they are only going to be used by the shader that
evaluates the samples.
3.4 Evaluating Samples
All the set S
i
for every point ~z
i
is evaluated in
this stage. The objective function is the residual
of Equation 1 applied to every 3D point for every
available frame:
argmin
j
t
∑
k=1
r
Π
R
k
~z
( j)
i
+
~
t
k
−~y
k
i
(3)
Equation 3 satisfies the independence needed in
stream processing, since each hypothesis is indepen-
dent from others.
Hypotheses are evaluated using a different shader
program. This shader runs once for each projection
~y
k
i
using texture ping-pong (Pharr, 2005), avoiding to
use loops inside the shader. The only data needed to
be transferred are the camera pose and the projection
of the 3D point for each frame. This shader program
must be executed t times for each 3D point.
When all the passes are rendered, the output
texture will contain the matrix with all the hypotheses
weighted. Now there are two ways to proceed. The
first one is to download the entire texture to main
memory and then search the best candidate using the
CPU. The second one is to search directly in the GPU.
Experimentally, we concluded that the second one is
the best way if the size of the texture is big enough.
This search is performed in a parallel fashion using
reduction techniques (Pharr, 2005).
4 EXPERIMENTAL RESULTS
Both precision and performance of the proposed
method have been measured in order to validating
it. All tests are executed on a real video recorded
in 320 × 240 using a standard webcam. Results are
compared with the implementation of the Levenberg-
Marquardt algorithm given by (Lourakis, 2004). In
our setup, the GPU optimizer runs with a viewport
of 256 × 256, reaching a total of 2
16
hypotheses per
point. The maximum number of iterations allowed to
the Levenberg-Marquardt algorithm is 200.
4.1 Precision
Various optimizations on triangulated 3D points have
been executed to measure the precision of the GPU
optimizer. In each run, 25 different points are re-
constructed using 15 consecutive frames tracked by
the algorithm described in (Eskudero et al., 2009).
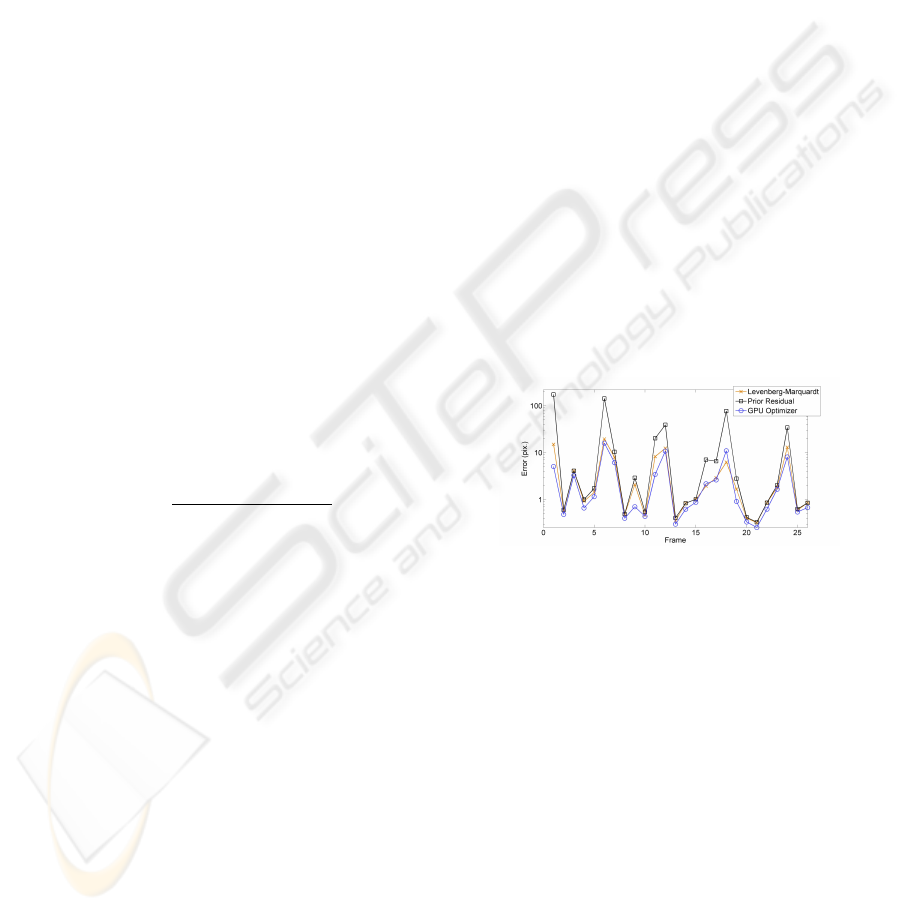
Figure 1 shows the mean reprojection residual. The
figure is in logarithmic scale. This test shows that the
GPU optimizer gets on average 1.4 times better re-
sults than Levenberg-Marquardt, demonstrating that
both Levenberg-Marquardt and GPU optimizer get
equivalent results.
Figure 1: Residual error on real images.
4.2 Performance
The PC used for performance tests is an Intel C2D
E8400 @ 3GHz with 4GB of RAM and a nVidia
GeForce GTX 260 with 896MB of RAM memory.
Following tests show the performance comparison be-
tween the GPU optimizer and Levenberg-Marquardt.
In Figure 2, 15 points are used, incrementing in each
time step the number of frames and Figure 3 shows a
test running with 10 frames incrementing the number
of points in each time step.
Note that both figures are in logarithmic scales.
Figure 2 shows that the GPU optimizer runs ap-
proximately 30 times faster than Levenber-Marquardt
when the number of frames is increased, being capa-
ble to run at 30fps. even when optimizing 15 points
over 60 frames.
Next tests analyze deeper the time needed by the
GPU optimizer in its different phases. Figure 4 shows
GPU OPTIMIZER: A 3D RECONSTRUCTION ON THE GPU USING MONTE CARLO SIMULATIONS - How to Get
Real Time without Sacrificing Precision
445

Figure 2: Performance with constant number of points.
Figure 3: Performance with constant number of frames.
the time needed to run the optimizer with 15 points
incrementing the number of frames in each time step,
and Figure 5 shows the the time needed when the
number of points to optimize is increased in each time
step, using always 10 frames.
Figure 4: Performance with constant number of points.
From Figure 4 follows that the point evaluation
is the only stage that depends on the number of
optimized frames. The total time depends linearly
on both number of points and number of frames
optimized as seen in Figure 5.
5 CONCLUSIONS
The proposed GPU optimizer runs a Monte Carlo
simulation locally on each point to be optimized,
making it very robust to outliers and highly adaptable
to different level of errors on the input data.
For validating it, a GPU implementation is
proposed and compared against the Levenberg-
Marquardt algorithm. Tests on real data show
that GPU optimizer can achieve better results than
Levenberg-Marquardt in much less time. This gain
of performance allows to use more data on the
optimization, obtaining better precision without
loosing the real time operation. Moreover, the GPU
implementation leaves the CPU free of computational
charge so it can dedicate its time to do other tasks. In
addition, the tests have been done in a standard PC
configuration using a standard webcam, making the
method suitable for middle-end hardware.
Figure 5: Performance with constant number of frames.
ACKNOWLEDGEMENTS
The contract of Jairo R. S
´
anchez is funded by the
Ministry of Education of Spain within the framework
of the Torres Quevedo Program and the contract
of Hugo
´
Alvarez is funded by a grant from the
Government of the Basque Country.
REFERENCES
Eskudero, I., S
´
anchez, J., Buchart, C., Garc
´
ıa-Alonso, A.,
and Borro, D. (2009). Tracking 3d en gpu basado
en el filtro de part
´
ıculas. In Congreso Espa
˜
nol de
Inform
´
atica Gr
´
afica, pages 47–55.
Lourakis, M. (Jul. 2004). levmar: Levenberg-
marquardt nonlinear least squares algorithms in
C/C++. http://www.ics.forth.gr/∼lourakis/levmar/+.
Metropolis, N. and Ulam, S. (1949). The monte
carlo method. Journal of the Americal Statistical
Association, 44(247):335–341.
Pharr, M. (2005). GPU Gems 2. Programing Techniques for
High-Performance Graphics and General-Purpose
Computing.
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
446
