MULTISPECTRAL TEXTURE ANALYSIS USING LOCAL BINARY

PATTERN ON TOTALLY ORDERED VECTORIAL SPACES

Vincent Barra

LIMOS, UMR 6158, Campus des C

ezeaux, 63173 Aubi

ere, France

Keywords:

Local binary pattern, Multispectral image, Segmentation, Texture, Total orderings.

Abstract:

Texture is an important feature when considering image segmentation. Since more and more image segmen-

tation problems involve multi- and hyperspectral data, including color images, it becomes necessary to deﬁne

multispectral texture features. In this article, we propose LMBP, an extension of the classical Local Binary

Pattern (LBP) operator to the case of multispectral images. The LMBP operator is based on the deﬁnition of

total orderings in the image space and on an extension of the standard univariate LBP. It allows the computa-

tion of both a multispectral texture structure coefﬁcient and a multispectral contrast parameter for each spatial

location, that serve as an input to an unsupervised clustering algorithm. Results are demonstrated in the case of

the segmentation of brain tissues from multispectral MR images, and compared to other multispectral texture

features.

1 INTRODUCTION

Texture analysis plays an important role in several ap-

plications, from remote sensing to medical image pro-

cessing, industrial applications or document process-

ing. Four major issues are expected in texture anal-

ysis: feature extraction, texture discrimination, tex-

ture classiﬁcation and shape from texture. To achieve

these analysis, several methods are available, using

statistical (autocorrelation, co-occurrence), geomet-

rical (structural techniques), model-based (MRF or

fractal) or signal processing based approaches (spa-

tial,Fourier, Gabor or wavelet ﬁltering) (see for exam-

ple (Tuceryan and Jain, 1998) for a review). Among

all these methods, the Local Binary Pattern (LBP) op-

erator offers an efﬁcient way of analyzing textures

(Ojala et al., 2002). It relies on a simple but efﬁcient

theoretical framework, and combines both structural

and statistical properties.

In the prementioned potential applications, color and

even multispectral data is more and more available

and the extension of texture analysis methods be-

comes natural. We propose in this article to extend

the LBP operator to the case of multispectral images.

Contrary to other works (Lucieer et al., 2005; Song

et al., 2006), we do not apply the univariate LBP on

scalar values derived from the multispectral dataset,

but directly propose a multispectral LBP operator,

based on a total ordering computed either in the im-

ages space, or in a derived vectorial space.

The paper is organized as follows: Section 2 ﬁrst

recall the original univariate LBP operator, and re-

call some basic deﬁnitions on orderings in a vectorial

space. It then introduces the LMBP - Local Multi-

spectral Binary Pattern, that uses both of these no-

tions. Section 3 presents and analyzes some prelim-

inary results of the operator on data stemming from

multispectral Magnetic Resonance Images.

2 LOCAL MULTISPECTRAL

BINARY PATTERN

2.1 Local Binary Pattern

Ojala et al. (Ojala et al., 2002) described the texture

T as the joint distribution of the gray levels of P + 1

image pixels: T = t(g

···g

p−1

), where g

is the

gray level value of the center pixel, surrounded by P

equally spaces pixels of gray levels g

, located on a

circle of radius R. Gray values g

were interpolated

if neighbors didn’t ﬁt on the pixel grid. They then

deﬁned the Local Binary Pattern (LBP), a grayscale

invariant and rotation invariant operator:

LBP

riu2

P,R







P−1

∑

i=0

σ(g

− g

) if U(LBP

P,R

) ≤ 2

P + 1 otherwise

where

Barra V. (2010).

MULTISPECTRAL TEXTURE ANALYSIS USING LOCAL BINARY PATTERN ON TOTALLY ORDERED VECTORIAL SPACES.

In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 37-43

DOI: 10.5220/0002828700370043

 SciTePress

U(LBP

P,R

) = |σ(g

P−1

− g

) − σ(g

− g

P−1

∑

i=1

|σ(g

− g

) − σ(g

i−1

− g

and σ(.) is the sign function. The uniformity function

U(LBP

P,R

) corresponds to the number of spatial tran-

sitions in the neighborhood: the larger it is, the more

likely a spatial transition occurs in the local pattern.

If LBP

riu2

P,R

captures the spatial structure of the texture,

it does not handle the strength of the pattern. To do

so, a contrast measure was deﬁned as

P,R

P−1

∑

i=0

− ¯g)

where ¯g =

P−1

∑

i=0

and textures may then be characterized by the joint

distribution of LBP

riu2

P,R

and C

P,R

Several extensions have been proposed to these fea-

tures (e.g. multi-resolution LBP (M

aenp

a and

Pietik

ainen, 2003; Ojala et al., 2002), center-

symmetric local binary pattern (Heikkil

a et al.,

2009)), and numerous applications have been

adressed using these techniques (e.g. face recogni-

tion (Ahonen et al., 2006), segmentation of remote-

sensing images (Wang and Wang, 2006), visual in-

spection (Paclik et al., 2002) or classiﬁcation of out-

door images (Garc

ıa and Puig, 2007)).

The LBP operator relies on the sign function σ(.),

and then on an ordering relation on the gray level

space. Since there is no natural ordering for vector

spaces, such as those produced by multispectral imag-

ing, the extension of LBP to multispectral data is not

straightforward. Some authors already deﬁned mul-

tispectral LBP by combining intra-plane and inter-

plane LBP relations (Lucieer et al., 2005), or by con-

sidering the univariate LBP on vector norms (Song

et al., 2006), but to our knowledge no LBP opera-

tor has directly be deﬁned on vectorial data. We thus

propose in the following to deﬁne the LMBP - Lo-

cal Multispectral Binary Pattern - operator, based on

LBP and on total orderings on R

. We ﬁrst recall ba-

sic deﬁnitions on orders and then introduce the LMBP

operator.

2.2 Total Orderings in R

We ﬁrst recall some basic deﬁnitions.

Deﬁnition 1. Let ≤

be a binary relation on a set P.

≤

is a pre-order if it is:

• reﬂexive: (∀x ∈ P) x ≤

• transitive: for all x,y,z ∈ P, if x ≤

y and y ≤

then x ≤

Deﬁnition 2. Let ≤

be a binary relation on a set

P. ≤

is a partial order if it is a pre-order and for all

x,y ∈ P, if x ≤

y and y ≤

x then x = y (antisymmetry)

Deﬁnition 3. Let ≤

be a partial order on a set P. ≤

is a total order if and only if for all x,y ∈ P, x ≤

y or

y ≤

If it is straightforward to deﬁne orders for scalar

values, the deﬁnition of partial -or total- orders for

vector valued data is not so easy: if data stems from

RGB images (P = R

), each channel being coded on

8 bits, each pixel can have one of the 2

possible

vectorial values, hence deﬁning 2

! possible total or-

derings.

One has then to ﬁnd another way to introduce order

in R

. Barnett (Barnett, 1976) deﬁned four ways to

order vectors: the marginal approach, the partial ap-

proach, the conditional order and the dimension re-

duction. This last technique is an usual way to pro-

ceed, (Goutsias et al., 1995), and consists either in

deﬁning an order using a distance in R

of each vec-

tor to a reference, or in projecting vectors into a vec-

torial space R

where an order can be deﬁned. In this

latter case, the projection is deﬁned by an applica-

tion h : R

→ R

, and (Chanussot and Lambert, 1998)

proved that :

• h deﬁnes an ordering relation ≤

in R

if and only

if h is injective (and h can be supposed to be bi-

jective if R

is restricted to h(R

))

• ≤

deﬁnes a total order in R

if and only if there

exist h : R

→ R

bijective deﬁning ≤

on R

and

q=1

• ≤

deﬁnes a total order in R

if and only if ≤

deﬁnes a space ﬁlling curve of R

Total ordering may then be identically handled by the

deﬁnition of h, or by the construction of a space ﬁll-

ing curve of R

. In the following, we propose as a

preliminary study to deﬁne ≤

using an appropriate

2.3 The LMBP Operator

Figure 1 presents an overview of the algorithm. Each

step is detailed in the following subsections

2.3.1 Subspace Analysis

Since numerous information may be available from

the original dataset of R

, and since the p original

images may be dependent, it may be useful to con-

duct feature extraction before deﬁning the vector or-

dering. Several techniques are available to extract

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

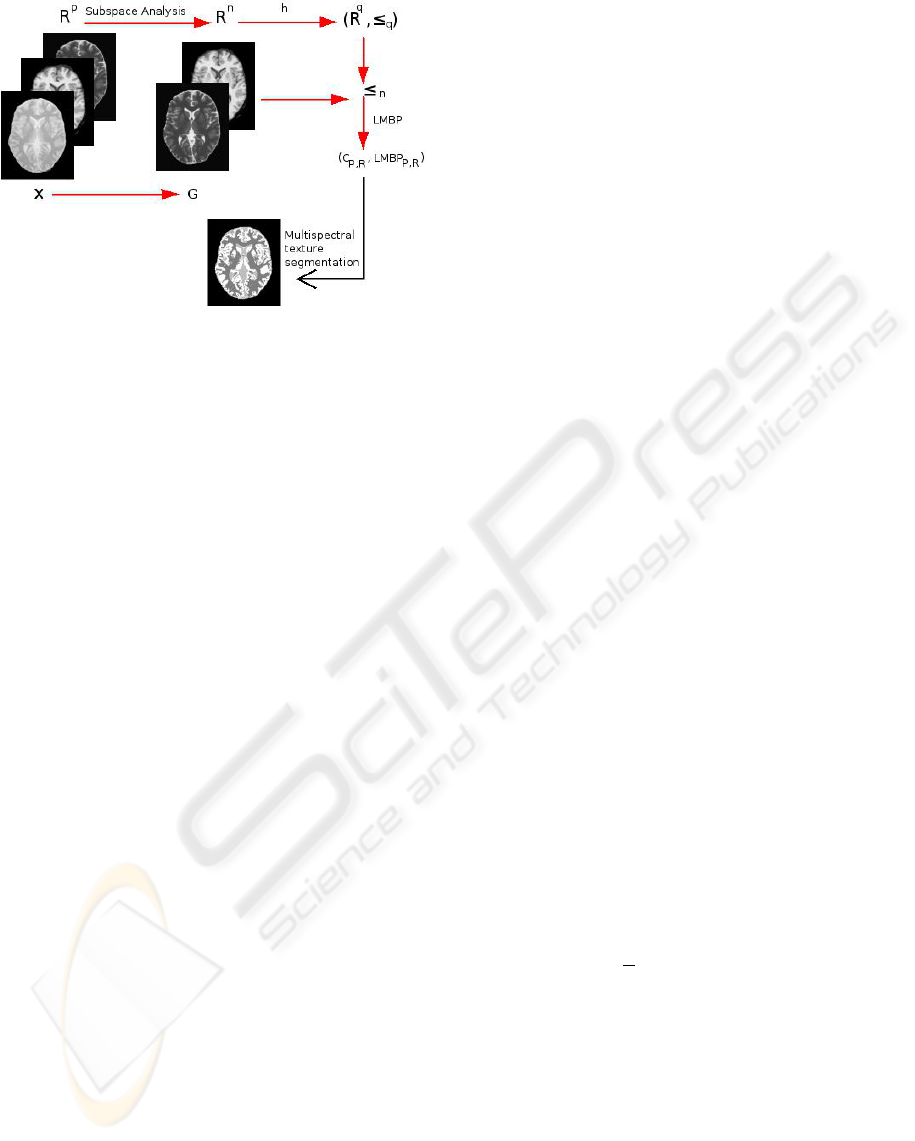
Figure 1: Overview of the algorithm.

features (Principal or Independent Component Anal-

ysis, Minimum Noise Fraction, or nonlinear tech-

niques such as Isomap or Local Linear Embedding).

In a preliminary study, we used a simple and linear

technique, the Principal Component Analysis (PCA),

that will directly impact the choice of the h function:

if X ∈ M

m,p

(R) denotes the matrix of the original

data (m being the number of pixels, p the number

of images and X

.,i

the i

column of X), the princi-

pal components are computed from the projections of

the original data onto the eigenvectors of Z

Z, where

Z = (X − 1µ)D is the matrix of centered and reduced

data, 1 = (1···1) ∈ R

,µ = (

.,1

···

.,p

) ∈ R

is the

vector of image mean values and D = diag(1/s

,1 ≤ i ≤ p is the standard deviation of variable i.

PCA allows n < p new variables to be computed, ex-

plaining most of the variance of the original data. The

resulting information is stored in G ∈ M

m,n

(R).

2.3.2 Deﬁnition of h

Recall that h : R

→ R

, an easily way to compute an

ordering relation in R

is to derive it from h using the

canonical ordering relation of R

,q ≥ 1:

x ≤

y ⇔ (∀1 ≤ i ≤ q, x(i) ≤ y(i))

This ordering relation is a partial order, and in the con-

text of image processing may lead to several draw-

backs: some vectors may not be ordered, and notions

of Sup and Inf are not deﬁned (and are compulsory in

areas such as mathematical morphology). In our con-

text, we thus decide to deﬁne a total ordering in R

then using q = 1 and h injective. Several choices are

possible (e.g. the bit mixing approach (Chanussot and

Lambert, 1998)), and we beneﬁt from the new basis

computed from PCA to use the lexicographic order in

deﬁned as:

x ≤

y ⇔ (∃k ∈ {1 ·· ·n})/x(i) = y(i),1 ≤ i ≤ k − 1, x(k) < y(k)

If each image is coded on b bits, the corresponding h

function is

h(x) =

∑

i=1

x(n + 1 − i)2

b(i−1)

2.3.3 Computation of LMBP

Once h has been deﬁned, an ordering relation on R

can be proposed as: x ≤

y ∈ R

⇔ h(x) ≤ h(y) ∈ R.

Unfortunately, enforcing a total ordering on R

makes

h discontinuous: the Netto theorem (Sagan, 1994)

indeed proved that any bijective application from a

manifold of dimension n to a manifold of dimension

q 6= n is discontinuous. Thus, h is not a linear func-

tion, and does not commute with linear functions.

It is thus not straightforward to assess h(x) − h(y),

given x − y in R

, and any linear combination of vec-

tors transformed by h should be avoided. If this is

not really a problem for the deﬁnition of the LBP

operator (σ(g

− g

) should easily be replaced with

σ(h(g

) − h(g

)) because the minus sign only means

to compare h(g

) with h(g

) using the ordering de-

ﬁned by h), the extension of C

P,R

to the case of multi-

spectral images is more problematic, because of both

¯g and the deviation to this mean value. In order to be

compliant with the discontinuity of h, we thus avoid

any linear combination, and replace ¯g by the median

value m

of the g

’s. The LBMP operator is then

LMBP

riu2

P,R







P−1

∑

i=0

σ(h(g

) − h(g

)) if U(LBP

P,R

) ≤ 2

P + 1 otherwise

where

U(LBP

P,R

) = |σ(h(g

P−1

) − h(g

)) − σ(h(g

) − h(g

))|

P−1

∑

i=1

|σ(h(g

) − h(g

)) − σ(h(g

i−1

) − h(g

))|

and the contrast operator

P,R

P−1

∑

i=0

(h(g

) − h(m

))

P,R

is still a combination of h(g

) − h(m

), but we

expect the nonlinearity introduced by m

to reduce

the discontinuity effects.

If h is computed from the lexicographic order, the sign

functions σ((h(x)−h(y))) in the previous expressions

reduce to

σ(

∑

j=1

(x(n + 1 − j) − y(n + 1 − j))2

b( j−1)

)

The ﬁrst components of x and y play here an impor-

tant role, as their difference is weighted by 2

b(n−1)

MULTISPECTRAL TEXTURE ANALYSIS USING LOCAL BINARY PATTERN ON TOTALLY ORDERED

VECTORIAL SPACES

but the other components, with weights 2

b. j

, j < n − 1

may invert the sign of the argument of the σ function.

Subspace analysis is thus a crucial step in the whole

process for the selection of relevant components.

2.3.4 From LMBP to Segmentation

Once LMBP and contrast have been computed for

each pixel location, we were interested in image seg-

mentation using these features. Several approaches

can be performed, e.g.:

• incorporate these operators in a vector describ-

ing the pixel properties, with other relevant val-

ues (e.g. values of the ﬁrst principal components).

The set of these vectors then serves as an input of

an unsupervised clustering algorithm

• compute a local 2D joint distribution (LMBP,C

P,R

)

for each pixel, and use an adapted metric to cluster

pixels.

In this preliminary study, we chose to use the ﬁrst al-

ternative. More precisely, a classical K-means algo-

rithm was used as a clustering method, using the Eu-

clidean metric to cluster feature vectors that the next

section will detail.

3 RESULTS

We apply the LMBP operator to the problem of mul-

tispectral MR image segmentation problem. As test

data we used simulated MRI-datasets generated with

the Internet connected MRI Simulator at the Mc-

Connell Brain Imaging Centre in Montreal

(www.bic.mni.mcgill.ca/brainweb/). The datasets we

used were based on an anatomical model of a normal

brain that results from registering and preprocessing

27 scans from the same individual with subsequent

semi-automated segmentation. In this dataset the dif-

ferent tissue types were well-deﬁned, both “fuzzy”

and “crisp” tissue membership were allocated to each

voxel. From this tissue labeled brain volume the MR

simulation algorithm, using discrete-event simulation

of the pulse sequences based on the Bloch equations,

predicted signal intensities and image contrast in a

way that is equivalent to data acquired with a real

MR-scanner. Both sequence parameters and the effect

of partial volume averaging, noise, and intensity non-

uniformity were incorporated in the simulation results

(Cocosco et al., 1997; Kwan et al., 1999).

Ten multispectral (T1-weighted,T2-weighted, Proton

density) MR datasets of a central slice (including the

main brain tissues, basal ganglia and ﬁne to coarse

details), with variations of the parameters ”noise” and

”intensity non-uniformity (RF)” were chosen (table

1), the slice thickness being equal to 1mm. This se-

lection covers the whole range of the parameter values

available in BrainWeb so that the comparability with

real data can be considered as sufﬁcient to test the ro-

bustness of the method at varying image qualities.

Table 1: MR Datasets.

dataset no dataset name noise RF

1 n1rf20 1% 20%

2 n1rf40 1% 40%

3 n3rf20 3% 20%

4 n3rf40 3% 40%

5 n5rf20 5% 20%

6 n5rf40 5% 40%

7 n7rf20 7% 20%

8 n7rf40 7% 40%

9 n9rf20 9% 20%

10 n9rf40 9% 40%

For obtaining the true volumes of brain tissues and

background the corresponding pixels were counted in

the ground truth image provided by BrainWeb.

We performed three types of analysis for each dataset,

ﬁrst transformed by a subspace analysis method

(namely the PCA). More precisely, we characterized

pixels with several types of feature vectors:

• either the vector of the ﬁrst principal components,

or a vector composed of the ﬁrst principal compo-

nents, the LMBP and the contrast operators (In-

terest of LMBP and Multispectral Contrast in the

segmentation process, section 3.1).

• either a vector composed of the ﬁrst principal

components, the LMBP and the contrast oper-

ators, or a vector composed of the ﬁrst princi-

pal components, the multispectral and the contrast

operators as computed in (Song et al., 2006) (sec-

tion 3.2)

In the following, we present results from dataset

n9rf20 (ﬁgure 2) and use as LBP parameters R =

1.5,P = 12. All features were normalized by their

max value to cluster homogeneous values.

3.1 Multispectral Texture Information

Figure 3 presents the results of the segmentation of

the brain slice in 4 classes: background (BG, light

gray), Cerebrospinal ﬂuid (CSF, dark gray), white

matter (WM, black) and gray matter (GM, white). S1

is the segmentation obtained with only the two ﬁrst

principal components, S2 with these two components

plus the LMBP and the contrast operator values.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

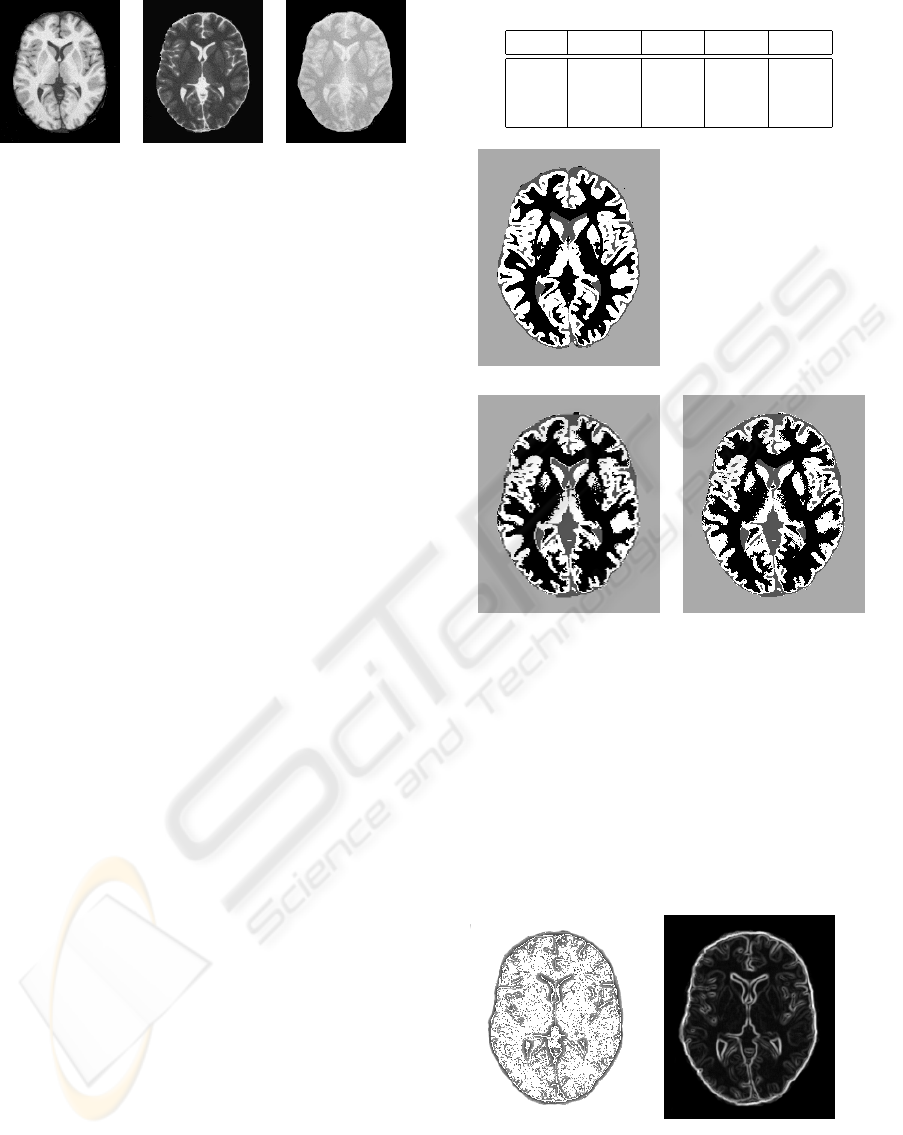
T1-weighted T2-weighted Proton Density

Figure 2: Slice of interest of dataset n9rf20.

In order to assess the two segmentations, we pro-

cess the confusion matrix C on the segmented images:

given a segmented image S, C

(i, j) is the percentage

of pixels assigned to class i ∈ {BG,CSF,W M, GM} in

the ground truth and to class j in S. The closer C to

a diagonal matrix, the better the segmentation is. Al-

though segmented images seems to be the same, the

confusion matrix reveal some differences:







48.4 10

−1

1.8.10

−3

0.44 4.64 1.58 0.83

0.06 0.12 19.28 4.62

0.13 0.89 0.71 18.2













48.3 0.10 2.10

−2

0.46 5.73 0.56 0.88

0.05 0.05 19.28 4.63

0.13 0.87 0.45 18.45







The multispectral texture coefﬁcients, and espe-

cially the LMBP operator, bring some information on

structural properties on tissue edges: interfaces be-

tween tissues are more or less expressed depending on

the acquisition (e.g. the CSF/(WM+GM) interface is

very clear in T2-weighted images, whereas the proton

density images better shows the WM/(GM+CSF) in-

terface), and the multispectral structure of edges, seen

as local oriented textures, is managed during the clus-

tering process (ﬁgure 4). It is particularly visible for

the WM/CSF interface between the corpus callosum

and the lateral ventricles (see image and C(2, 3) coef-

ﬁcient) and for the WM/GM interface near the puta-

mens (see image and C(4,3) coefﬁcient).

Table 2 shows the number of pixels assigned to

each class. Relative errors for S1 (respectively S2)

are 0.01 (0.01) for background, 0.31 (0.31) for CSF,

0.11 (0.06) for WM and 0.15 (0.11) for GM. For WM

and GM, relative errors lower due to the integration

of LBMP operators.

3.2 LMBP vs. Another Multispectral

Texture Deﬁnition

We also compared the LMBP operator with a mul-

tispectral LBP already proposed in the litterature

(Song et al., 2006), that compute LBP as:

Table 2: Number of pixels in each class.

BG CSF WM GM

truth 19826 2336 8741 9577

S1 19620 3039 9755 8066

S2 19601 3088 9328 8463

Ground truth

S1 S2

Figure 3: Segmentation results.

LBP

riu2

P,R







P−1

∑

i=0

σ(kg

k − kg

k) if U(LBP

P,R

) ≤ 2

P + 1 otherwise

where norms also stand in the deﬁnition of U. As

in (Song et al., 2006), we used the Euclidean norm,

and the LBP parameters were chosen equal to those

of LMBP. Note that this method is a particular case of

LMBP, with h : x 7→ kxk.

LBMP Contrast

Figure 4: LBMP and Contrast images.

Figure 5 shows LMBP and Contrast images for

both methods, and ﬁgure 6 compares the two seg-

MULTISPECTRAL TEXTURE ANALYSIS USING LOCAL BINARY PATTERN ON TOTALLY ORDERED

VECTORIAL SPACES

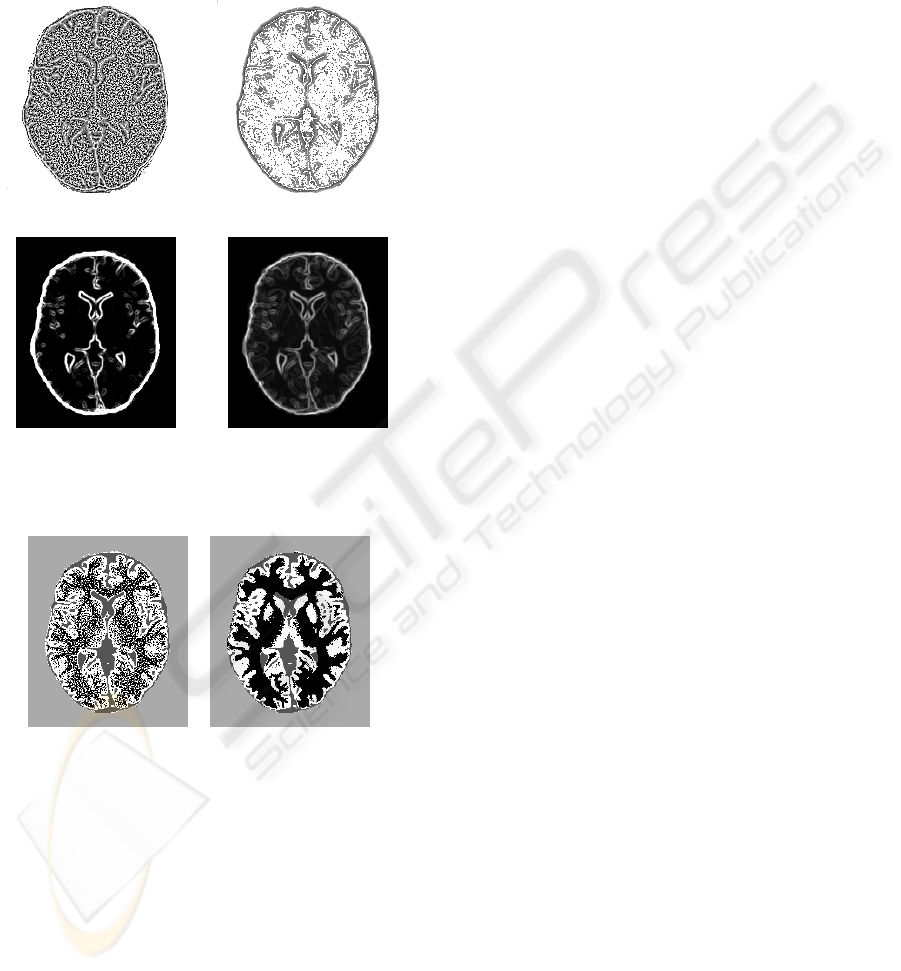
mentations. Results were always much better using

LMBP for all the MR volumes described in Table 1,

and the difference increased as the noise increased in

the image. The function h : x 7→ kxk used to produce

the total ordering in R

indeed tended to increase the

lbp value in a noisy neighborhood of a pixel g

, pro-

ducing the noisy LBP image of ﬁgure 5.

(Song et al., 2006) LBP LMBP

(Song et al., 2006) contrast LMBP Contrast

Figure 5: Comparison of multispectral LBP and Contrast

images.

(Song et al., 2006) LMBP segmentation

segmentation

Figure 6: Comparison of segmentation results.

4 CONCLUSIONS

We proposed in this article a multispectral version of

the classical Local Binary Pattern operator, based on

a total ordering on the vectorial space of the data. We

demonstrate its efﬁciency on multispectral MR im-

ages of the brain, assessing the results with respect to

a ground truth, and comparing segmentation results

with those provided by another multispectral LBP ap-

proach.

Numerous perspectives are now expected from this

preliminary work. First of all, h needs to be better

deﬁned to allow the local topology to be preserved:

two neighbors in R

need to stay closed when trans-

formed by h. For x and y neighbors in R

, the solu-

tion may be to deﬁne h using space ﬁlling curves di-

rectly on the multispectral image, in order to impose

small variations of h(x)−h(y) in areas of interest, and

higher variations for example in the background.

The segmentation scheme also needs to be reﬁne. For

this study, standard techniques (PCA, Kmeans) were

applied, and some work has now to be done to tune

subspace analysis and segmentation methods to this

speciﬁc problem. Finally, this multispectral approach

ﬁnds natural applications not only in medical imag-

ing, but also in remote sensing imagery. We now in-

tend to tune and apply the LMBP to this domain.

REFERENCES

Ahonen, T., Hadid, A., and Pietik

ainen, M. (2006). Face

description with local binary patterns: Application to

face recognition. IEEE Trans. Pattern Anal. Mach.

Intell., 28(12):2037–2041.

Barnett, V. (1976). The ordering of multivariate data. Jour-

nal of the Royal Statistical Society, Series A, 139:318–

355.

Chanussot, J. and Lambert, P. (1998). Total ordering based

on space ﬁlling curves for multivalued morphology.

In ISMM ’98: Proceedings of the fourth international

symposium on Mathematical morphology and its ap-

plications to image and signal processing, pages 51–

58, Norwell, MA, USA. Kluwer Academic Publish-

ers.

Cocosco, C. A., Kollokian, V., Kwan, R. K. S., Pike, G. B.,

and Evans, A. C. (1997). Brainweb: Online interface

to a 3d mri simulated brain database. NeuroImage, 5.

Garc

ıa, M. A. and Puig, D. (2007). Supervised texture

classiﬁcation by integration of multiple texture meth-

ods and evaluation windows. Image Vision Comput.,

25(7):1091–1106.

Goutsias, J. K., Heijmans, H. J. A. M., and Sivakumar,

K. (1995). Morphological operators for image se-

quences. Computer Vision and Image Understanding,

62(3):326–346.

Heikkil

a, M., Pietik

ainen, M., and Schmid, C. (2009). De-

scription of interest regions with local binary patterns.

Pattern Recogn., 42(3):425–436.

Kwan, R., Evans, A., and Pike, G. (1999). Mri simulation-

based evaluation of image-processing and classiﬁca-

tion methods. 18(11):1085–1097.

Lucieer, A., Tsolmongerel, O., and Stein, A. (2005). Multi-

variate texture-based segmentation of remotely sensed

images. International Journal of Remote sensing,

26:2917–2936.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

aenp

a, T. and Pietik

ainen, M. (2003). Multi-scale binary

patterns for texture analysis. pages 885–892.

Ojala, T., Pietikinen, M., and Menp, T. (2002). Multires-

olution gray-scale and rotation invariant texture clas-

siﬁcation with local binary patterns. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

24(7):971–987.

Paclik, P., Duin, R. P., Kempen, G. M. P. V., and Kohlus,

R. (2002). Supervised segmentation of textures in

backscatter images. In In: Proceedings of IEEE In-

ternational Conference on Pattern Recognition, pages

490–493. John Wiley and Sons.

Sagan, H. (1994). Space Filling Curves. Springer Verlag.

Song, C., Li, P., and Yang, F. (2006). Multivariate texture

measured by local binary pattern for multispectral im-

age classiﬁcation. In In: Proceedings of IEEE Inter-

national Conference on Geoscience and Remote Sens-

ing Symposium, pages 2145–2148.

Tuceryan, M. and Jain, A. K. (1998). Texture analysis, vol-

ume 15 of Handbook of Pattern Recognition and Com-

puter Vision, Second Edition, pages 207–248. World

Scientiﬁc, c.h. chen, and l.f. pau edition.

Wang, A. P. and Wang, S. G. (2006). Content-based high-

resolution remote sensing image retrieval with local

binary patterns. In Society of Photo-Optical Instru-

mentation Engineers (SPIE) Conference Series, vol-

ume 6419 of Society of Photo-Optical Instrumentation

Engineers (SPIE) Conference Series.

MULTISPECTRAL TEXTURE ANALYSIS USING LOCAL BINARY PATTERN ON TOTALLY ORDERED

VECTORIAL SPACES