MULTISCALE VISUALIZATION OF RELATIONAL DATABASES

USING LAYERED ZOOM TREES AND PARTIAL DATA CUBES

Baoyuan Wang, Gang Chen, Jiajun Bu

College of Computer Science and Technology, Zhejiang University, Hangzhou, China

Yizhou Yu

University of Illinois at Urbana-Champaign, U.S.A.

Zhejiang University, Hangzhou, China

Keywords:

Database, Visualization, Data cubes, H-tree, GPGPUs.

Abstract:

The analysis and exploration necessary to gain deep understanding of large databases demand an intuitive and

informative human-computer interface. In this paper, we present a visualization system with a client-server

architecture for multiscale visualization of relational databases. The visual interface on the client supports

web-based remote access. We use zoom trees to represent the entire history of a zooming process that reveals

multiscale details. Every path in a zoom tree represents a zoom path and every node in the tree can have

an arbitrary number of subtrees to support arbitrary branching and backtracking. Zoom trees are seamlessly

integrated with a table-based overview using ”hyperlinks” embedded in the table. To support fast query pro-

cessing on the server, we further develop efﬁcient GPU-based parallel algorithms for online data cubing and

CPU-based data clustering. Also, a user study was conducted to evaluate the effectiveness of our design.

1 INTRODUCTION

With increasing capabilities in data collection, large

databases are being produced at an unprecedented

rate. Examples include corporate data warehouses

archiving their operations such as sales and market-

ing, databases archiving historical climate changes,

historical census databases as well as large-scale gene

expression databases. A major undertaking with these

large-scale databases is to gain deeper understanding

of the data they contain: to identify structures and

patterns, discover anomalies, and reveal dependencies

and relationships.

The analysis and exploration necessary to achieve

these goals demand intuitive and informative human-

computer interfaces to these databases. There exist

challenges in developing such a powerful visual in-

terface. First, analysts working on databases often

need to see an overviewﬁrst, then progressivelyzoom

into details. How can we design an interface that

can seamlessly integrate overview and zoom capabil-

ities? Second, the path of exploration is unpredictable

and may rapidly change. Instead of predeﬁned zoom

paths, the interface should be able to support dynami-

cally formed zoom paths. Furthermore, the history of

a zooming process should have a tree structure where

any node can have an arbitrary number of branches

for zooming into different local regions of the dataset.

How can we support arbitrary branching and back-

tracking in a zooming process and how can we ef-

fectively visualize the tree structure without wasting

screen space?

Data cubes are a common method for abstract-

ing and summarizing relational databases (Gray et al.,

1997). Cuboids in a data cube store pre-aggregated

results that enable efﬁcient query processing and on-

line analytical processing (OLAP) (Chaudhuri and

Dayal, 1997; Mansmann and Scholl, 2007). Com-

putationally intensive aggregation is thus replaced

by fast lookup operations over the precomputed data

cube. By representing the database with a data cube,

one can quickly switch between different levels of de-

tail. However, for high-dimensional datasets, a fully

materialized data cube may be orders of magnitude

larger than the original dataset. It is only practical to

precompute a subset of the cuboids. Previous work

has demonstrated that online data cubing based on a

partial data cube can still signiﬁcantly shorten query

response times. In the current context, a critical chal-

lenge with data abstraction is how to further reduce

101

Wang B., Chen G., Bu J. and Yu Y. (2010).

MULTISCALE VISUALIZATION OF RELATIONAL DATABASES USING LAYERED ZOOM TREES AND PARTIAL DATA CUBES.

In Proceedings of the International Conference on Imaging Theory and Applications and International Conference on Information Visualization Theory

and Applications, pages 101-111

DOI: 10.5220/0002829301010111

 SciTePress

query processing time to achieve interactive perfor-

mance using a partial data cube.

In this paper, we present solutions to the afore-

mentioned challenges and develop a complete visu-

alization system for multiscale visualization of rela-

tional databases. This paper has the following contri-

butions.

• We propose to use a tree structure called zoom

trees to represent the history of a zooming process

that revealsmultiscale details. Zoom trees support

arbitrary branching and backtracking.

• Zoom trees are seamlessly integrated with a table-

based overview using automatically generated

”hyperlinks” embedded in every chart of the ta-

ble. Once a user clicks any of these links, a new

zoom tree is initiated on a new layer.

• We further propose to use graphics processors

(GPUs) to perform real-time query processing

based on a partial data cube. We develop an ef-

ﬁcient GPU-based parallel algorithm for online

cubing and a CPU-based algorithm for grid-based

data clustering to support such query processing.

• We integrate all components together into a com-

plete client-server system. The client is Flash

based and supports web-based remote access.

Queries and processing results are communicated

between the client and server via a network con-

nection. Queries are automatically generated ac-

cording to user interactions.

2 RELATED WORK

2.1 Multi-Dimensional Dataset

Visualization

Over the decades, much work (Antis et al., 1996;

Weijia Xu, 2008) has been done on visualizing

relational database to uncover hidden casual rela-

tions. Lots of visualization techniques for multi-

dimensional datasets have been designed including

parallel coordinates, scatter plot matrices, and dense-

pixel display.

Recently, more and more databases are augmented

with data cubes which provide meaningful levels of

abstraction. To integrate humans into the exploration

process and uncover the hidden patterns more intu-

itively and easily, lots of data cube visualization tech-

niques have been developed. A pioneering database

visualization system called Polaris (Stolte et al., 2002)

visually extends the Pivot table (Inc, 2007) by using

various graphical marks instead of text. It provides

multiscale cube visualization in the form of zoom

graphs and four design patterns (Stolte et al., 2003).

However, the drawbacks of polaris include poor scal-

ability over large datasets and only predeﬁned zoom

graphs are supported. The meaning of scalability is

twofold. It refers to both query response time and

screen space clutter over large datasets. The visu-

alization system in this paper overcomes these lim-

itations. (Maniatis et al., 2003) proposed a method

to map the cube presentation model (CPM) to Ta-

ble Lens (Rao and Card, 1994), which is a well-

known distortion technique. Based on hierarchical

dimensional visualization (HDDV (Kesaraporn et al.,

2004)), (Techapichetvanich and Datta, 2005) pro-

posed an interactive cube visualization framework

which uses horizontal stack bars to represent dimen-

sions, and roll-up and drill-down operations are im-

plemented through directly manipulating these bars.

(Pro, ) was the ﬁrst to introduce a hierarchical drill-

down visualization called decomposition trees, based

on which (Mansmann and Scholl, 2007) introduced

enhanced decomposition trees. Our proposed hier-

archical zooming technique is partially inspired by

(Rep, ), which provides a web-based reporting solu-

tion. The client offers different types of chart trees,

and drill-down operations are implemented by ex-

panding speciﬁed bars along potentially different di-

mensions. Semantic zooming interfaces were devel-

oped in Pad++ (Bederson and Hollan, 1994), DataS-

plash (Allison et al., 2001) and XmdvToll (Runden-

steiner et al., 2002).

One challenging problem facing visualization sys-

tems is their scalability with large datasets because an

overcrowded visual presentation has a negative im-

pact on the analysis process. To reduce clutter and

make visualizations more informative to end-users, a

variety of techniques and algorithms have been de-

signed. (Fua et al., 1999; Kreuseler and Schumann,

1999) proposed a multiresolutional view of data via

a hierarchical clustering method for parallel coordi-

nates. (Peng et al., 2004) proposed to use dimension

reordering for a variety of visualization techniques in-

cluding star glyph and scatter plots. However, to the

best of our knowledge, no clustering techniques have

been proposed to support charting large datasets, es-

pecially for plot charts. A taxonomy of clutter reduc-

tion for visualization can be found in (Ellis and Dix,

2007).

2.2 Data Cubes

Data cubes categorize database ﬁelds into two classes:

dimensions and measures, corresponding to the in-

dependent and dependent variables, respectively. A

IVAPP 2010 - International Conference on Information Visualization Theory and Applications

102

data cube consists of a lattice of cuboids, each of

which corresponds to a unique data abstraction of the

raw data. A data abstraction is deﬁned by a speciﬁc

projection of the dimensions. A cuboid is abstractly

structured as an n-dimensional cube. Each axis cor-

responds to a dimension in the cuboid and consists of

every possible value for that dimension. Each ”cell”

in the cuboid corresponds to a unique combination of

values for the dimensions. Each ”cell” also contains

one value per measure of the cuboid. H-tree based

cubing was initially proposed by (Han et al., 2001) for

iceberg cubes and later extended to support stream-

ing data (Han et al., 2005). In this paper, we develop

a technique for interactively exploring the aggregates

by using an H-tree as a partially materialized cube.

Figure 1: System Architecture.

3 SYSTEM ARCHITECTURE

We adopt the classic client-server architecture for our

visualization system (Figure 1). We chose to develop

the visual interface in Flash on the client side. Flash

exhibits multiple advantages in this task. First, it is

cross-platform and can be easily embedded into most

of the web browsers. Furthermore, ﬂash code written

in ActionScript is interpreted and executed at run time

by the Flash Player which is commonly preinstalled

on personal computers. This makes our visualiza-

tion system web-based and readily availableto remote

users. Second, ActionScript, the scripting language

for Flash, facilitates user interface development and

has a charting component that supports the drawing

of basic charts, including bar charts, pie charts, and

plot charts, which are among the elementary building

blocks of our visual interface.

Our visual interface supports a wide variety of

user interactions to help the user visually analyze the

database under consideration. Most of these interac-

tions are transformed into a number of queries ac-

cording to a predeﬁned formalism. Then all these

queries are sent to the server via a network connec-

tion. The server has both a CPU component and a

GPU component. The CPU component is mainly re-

sponsible for data clustering and communication with

the client while the GPU component, which serves as

a coprocessor, performs most of the computationally

intensive tasks, including query processing and data

bounding box evaluation. The processing results are

formatted into an XML ﬁle on the CPU and sent back

to the client.

4 VISUAL INTERFACE

In this section, we introduce our proposed visual ab-

straction. We would like to achieve the following

overall design goals.

1. Dense display of various types of charts for efﬁ-

cient utilization of the screen space

2. Interactive subcube selection for setting focus of

the analysis

3. A powerful and ﬂexible zoom interface for detail

investigation

We address these design goals by incorporating three

main user interface components, schema-based nav-

igation for subcube selection, a table-based layout

for an overview of the selected subcube, and layered

zoom trees for the exploration of details. We elabo-

rate these components in the following subsections.

4.1 Schema based Subcube Selection

Instead of analyzing the entire data cube at once, users

usually would like to focus on a subset of the dimen-

sions every time. A subcube is deﬁned by a subset

of the dimensions. Each of the remaining dimensions

is ﬁxed to a speciﬁc value. In a data cube, a sub-

cube can be speciﬁed with slice/dice operations. In

our system, slice/dice operations are implemented us-

ing the schema list shown in a control panel (Fig. 2).

The schema is visualized as a hierarchical tree struc-

ture with each dimension represented as a node in the

tree. If a user left-clicks a node, all the possible val-

ues of the dimension are presented in a pop-up list.

The user can choose whatever value by clicking the

corresponding check-box to the left of the value. A

slice operation performs a selection on one of the di-

mensions while a dice operation deﬁnes a subcube by

performing two or more slice operations. Users can

perform either operations on the schema. (Mansmann

and Scholl, 2007) proposed a similar schema naviga-

tion. However, there is a major difference between

MULTISCALE VISUALIZATION OF RELATIONAL DATABASES USING LAYERED ZOOM TREES AND

PARTIAL DATA CUBES

103

(a) (b) (c)

Figure 2: Schema based subcube selection. (a) shows the

initial stage. If the user would like to view a slice of the

data for the state, ”Florida”, he descends into the ”Location”

hierarchy, clicks the ”States” node, and selects ”Florida” in

the pop-up list shown in (c).

them. For a dimension with an overly large cardinal-

ity, our system automatically builds a hierarchical list

for distinct values in the dimension so that an item at

an intermediate level represents a range of values. It

would be impossible to show all values in the dimen-

sion on the screen without such a hierarchical list.

4.2 Table based Overview

Once a target subcube has been selected, the user can

generate an overview of the subcube by conﬁguring

the axes of a 2D table-based visualization component

which was inspired by Polaris (Stolte et al., 2002)

and Pivot Table (Inc, 2007). The table based visu-

alization is able to reveal high-level trends and corre-

lations in the chosen subcube. More detailed infor-

mation can be progressively fetched through zoom-

ing or drill-down operations. Unlike Polaris, at most

two nested database dimensions (measures) can be

mapped along the horizontal or vertical direction of

the table to achieve simplicity and clarity. Four pull-

down lists on the interface allow the user to conﬁgure

the table by choosing the dimensions and measures

assigned to the two outer axes and two inner axes and

the visual presentation is automatically determined by

the conﬁguration of these axes (Fig. 3).

As usual, our table-based overview supports vari-

ous interactive operations on data cubes. Such oper-

ations include pivoting, roll-up, drill-down, ﬁltering

and sorting. To facilitate side-by-side comparisons,

the user can also reorder rows and columns in the ta-

ble by dragging desired ones together.

4.3 Zoom Trees for Detail Visualization

Zooming is a frequently used operation in visualiz-

ing multi-dimensional relational databases and data

cubes. In this section we propose to use zoom trees

on separate layers for facilitating the presentation of

zooming results along with the zooming history.

4.3.1 Layered Zoom Trees

Given an overview of a selected subcube in our table-

based visualization component, visual analysts typi-

cally need to dig deeper into the subcube to gain more

insights or discover correlations and anomalies. Since

the table-based overview can only accommodate up to

four dimensions/measures, the remaining dimensions

are aggregated together. To discover more details,

zooming needs to disaggregate such dimensions or

expand an existing dimension to expose more detailed

levels. A zooming process in our system is purely

event driven, and it always begins with a chart in the

table-based overview. The events embedded into the

chart (in the table) serve as ”hyperlinks”. For exam-

ple, a user can initiate a zooming process by clicking

any bar in a bar chart or select a region of interest in

a plot chart in the table (Fig. 4). Any event triggered

by such user interactions pops up a new active layer.

The chart clicked by the user becomes the root of a

new zoom tree initiated on this layer, and the disag-

gregated information corresponding to the chosen bar

or region is presented in a new chart, which becomes

a child of the root. The user can continue to zoom into

any existing node in this tree, and a new child of the

existing node is spawn holding the zooming results.

To reduce screen space clutter, at any time, only

one path from the root to a leaf in the tree is visu-

alized, and all other nodes in the tree are hidden. A

path in a zoom tree is presented in a predeﬁned layout

within the layer, where the nodes are arranged from

left to right horizontally and from top to bottom verti-

cally. Each node in the tree is a chart, and represents

a disaggregation of a dimension or an intermediate

level of a hierarchically clustered dataset. A user can

dynamically change the type of chart shown within a

node. The user can also minimize (deactivate) and re-

activate a layer. There can be only one active layer at

any time.

There are three operations supported for zoom

trees.

1. Add nodes. Double-click a bar or a pie or select

a region in a plot chart, a list of dimensions will

pop up. Once the user has chosen one of the di-

mensions, a new chart will be generated as a new

child node.

2. Delete nodes. Nodes can be deleted by directly

clicking the ”Delete” button on each chart. If a

node is deleted, all its descendants are pruned at

the same time.

3. Show/Hide nodes. Since our system only shows

one path from the root to a leaf in the tree, the

user can choose a desired branch by clicking the

radio button representing the root of the subtree.

IVAPP 2010 - International Conference on Information Visualization Theory and Applications

104

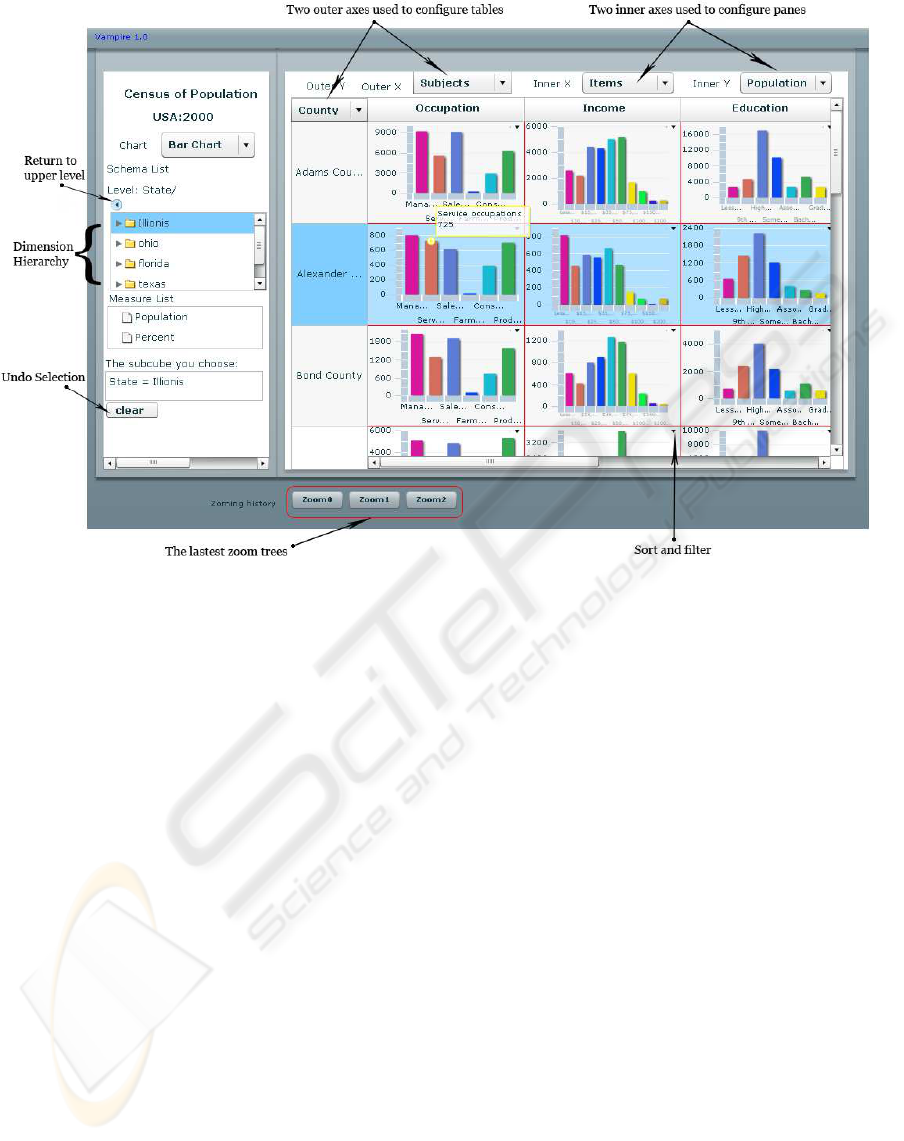
Figure 3: Overview of the visual interface. The schema list is in the left panel. There are four pull-down lists at the top of

the right panel for table conﬁguration. Minimized zoom trees are listed at the bottom of the window. The above screenshot

visualizes census information of Illinois, including statistics on education, occupation, income, industry and so on.

All sibling nodes of the chosen branch and their

decedents become all hidden.

Compared with decomposition trees in (Mans-

mann and Scholl, 2007) and semantic zooming in

the Pad++ system (Bederson and Hollan, 1994), our

zoom trees have two unique characteristics. First, a

zoom tree has a generic tree structure recording the

entire history of a zooming process performed on a

chart in the overview. Unlike previouswork, a node in

a zoom tree can have an arbitrary number of children.

But at any time there is only one child visualized to

efﬁciently utilize screen space. Second, pivoting is

supported during a zooming process. It provides ad-

ditional dynamic views of the data and, therefore, hid-

den patterns could be discovered more easily. There

are two types of zooming according to the data type

it operates on. One is for data with aggregated di-

mensions and the other is for data clusters which are

computed from either raw or aggregated data points

to reduce screen space clutter.

4.3.2 Zooming Aggregated Data

This type of zooming applies to bar charts and other

types of charts essentially equivalent to bar charts,

such as pie charts and line charts. During a zoom-

ing step, the user chooses a bar and disaggregates it

along a dimension that is different from the dimension

mapped to one of the axes of the chart (Fig. 4(a)&(c)-

(e)). Note that different bars in the same chart can

be disaggregated along different dimensions. Such

a zooming step essentially performs local drill-down

over a subset of aggregated data. The ﬂexibility of

such zooming steps facilitates detailed data explo-

ration.

4.3.3 Zooming Data Clusters in Plot Charts

There can be a huge number of data points in a plot

chart while the screen area allocated for the chart is

often quite limited. Overly crowded points in a plot

chart can prevent users from identifying the underly-

ing correlations and patterns. To reduce this type of

screen space clutter, we perform clustering on the data

points using screen space distance, and only visual-

ize the cluster centers in the plot chart. Every cluster

center is visualized as a small circle whole radius in-

dicates the number of data points in the underlying

cluster. The clustering algorithm is executed on the

CPU which takes the screen location of the raw data

points and the number of desired clusters as input (see

Section 6.2). Zooming such data clusters can be initi-

MULTISCALE VISUALIZATION OF RELATIONAL DATABASES USING LAYERED ZOOM TREES AND

PARTIAL DATA CUBES

105

(a) (b)

(e) (f)

Figure 4: (a)&(c)-(e) show a series of screenshots for a multiscale visualization of a coffee chain database, which has been

abstracted into an eight dimensional partial data cube. The table in (a) has the sixth type of conﬁguration stated in Section

4.2. When a user would like to disaggregate ”Proﬁt” in ”February”, he should left-click the corresponding ”pie” of the pie

chart in the top-left pane. He will be presented a list of aggregated dimensions. The user selects ”Market” as the dimension to

be disaggregated, and a new zoom tree will be initiated. (c)-(e) show three different views of this zoom tree. The view in (d)

is obtained by pivoting the second node from ”MarketType” to ”Product”. And (e) is obtained by clicking the second branch

from the root. This operation automatically hides the ﬁrst subtree of the root. Note that there is a caption in the header of

each node to indicate its scope. (b)&(f) show two screenshots with plot charts visualizing historical climate records including

”Temperature”, ”Precipitation”, and ”Solar Radiation” in US during the last century. Such visualizations enable analysts to

discover potential relationships among these measurements. The view in (f) is obtained by zooming into a region in a pane of

the table in (b). Note that the views in (c)-(f) are displayed on pop-up layers above the original table.

ated by drawing a rectangular region of interest (Fig.

4(b)&(f)). Cluster centers falling into the region are

automatically selected. A new chart is created as a

child of the current node in the zoom tree displaying a

zoomed view of the region. This zoomed view is gen-

erated on the ﬂy by calling the clustering algorithm on

the server again over those raw data points falling into

the selected region. Because the selected region is

zoomed to cover the area of an entire chart, the num-

ber of resulting cluster centers becomes larger than

that in the selected region of the original chart. Such

a zooming step can be recursively performed until the

number of raw data points within the region is less

than a threshold. Note that zooming clustered data

does not involve any aggregated dimensions.

4.3.4 Pivoting During Zooming

It would be desired to gain more insight during data

analysis by generating additional views of a node in

a zoom tree. Users can achieve this goal with the

help of pivoting. Unlike pivoting discussed in Sec-

tion 4.2 where the axis conﬁguration of the entire ta-

ble is changed, pivoting here is only applied locally to

IVAPP 2010 - International Conference on Information Visualization Theory and Applications

106

a chart in a particular tree node and can be performed

on any node in the zoom tree. For this purpose, users

can directly click the pull-down list along the dimen-

sion axis of the chart and choose the desired dimen-

sion for the new view. We restrict the target dimen-

sion for pivoting to be selected from the remaining

dimensions which have not been used so far.

5 QUERY FORMATION

In this section, we brieﬂy discuss how to transform

user interactions into queries and how these queries

are expressed according to a predeﬁned formalism.

5.1 Query Formalism

Since we adopt the H-Tree (Han et al., 2001) as

the implementation of our partial cube, typical cube

query languages such as MDX can not be used to de-

scribe a query. Therefore we develop a simple H-

tree based partial cube query formalism. Generally,

there are two kinds of queries for data cubes:(1) point

query and (2) subcube query. A point query only in-

cludes a few instantiated dimensions but without any

inquired dimensions. On the other hand, a subcube

query is required to include at least one inquired di-

mension. We use ”?” to represent an inquired dimen-

sion, ”*” to represent a ”Not care” dimension, and a

string of values demarcated by slash(”/”) to represent

an instantiated dimension. Assume the partial cube is

constructed from a relational database with M dimen-

sions and K measures. There exists a predeﬁned order

of the dimensions, D

,...,D

, typically speciﬁed

by OLAP experts. In such a context, the two kinds of

queries can be expressed in a formalism used by the

following two examples:

< ∗,∗,d

,∗,...,∗; m

,...,m

>, (1)

< ∗,?,d

,?,...,∗; m

,...,m

>, (2)

where m

(1 ≤ i ≤ K) represents the label of a mea-

sure, m

= 1 if it is inquired otherwise it is set to 0;

and d

are two speciﬁed values for the instan-

tiated third dimension. There are two parts in each

query. The ﬁrst part is reserved for the dimensions

demarcated by commas(”,”) and the second part is for

the labels of the measures also demarcated by com-

mas. Note that there could be more than one val-

ues speciﬁed for each instantiated dimension. (1) de-

scribes a point query, which returns one aggregated

value for each inquired measure. (2) describes a sub-

cube query with the second and fourth dimensions as

inquired dimensions.

5.2 Query Generation

Queries similar to (1) and (2) are generated by tracing

user interactions and ﬁlling slots corresponding to di-

mensions relevant to the interactions. Note that, there

can be only three types of values for each slot: ”*”,

”?” or a string of instantiated values.

Slice/Dice Selection. As discussed in Section 4.1,

slice and dice only specify instantiated dimensions.

Thus, values of the instantiated dimensions will be di-

rectly ﬁlled into the corresponding slots of the query.

For example, if we selected ”2007” and ”2008” as the

values for the dimension ”Year”, the ”Year” slot will

be ﬁlled with ”2007/2008” in all subsequent queries.

Query Generation for Table-based Overview. As

stated in Section 4.2, four of the six types of com-

monly used axis conﬁguration generate tables of

charts, and the other two generate a single large bar

chart or plot chart. In the ﬁrst type of conﬁguration

mentioned in Section 4.2, there is only one dimension

speciﬁed, therefore, only one subcube query is gener-

ated taking the dimension assigned to the outer ver-

tical axis as the inquired dimension and all the mea-

sures as the inquired measures. The second type of

conﬁguration is a special case of the ﬁrst one since it

only inquires one measure. A 2D table can be gen-

erated by assigning two dimensions to the two outer

axes. Once speciﬁed, the whole table is divided into

a 2D grid of panes each of which maps to a speciﬁc

pair of values of the dimensions assigned to the outer

axes. A subcube query is generated for each pane.

The actual query type depends on whether there is a

dimension assigned to the inner axes. For instance,

in the fourth type of conﬁguration in Section 4.2, one

subcube query is generated for each pane taking the

inner horizontal dimension as the inquired dimension.

In the ﬁfth type of conﬁguration, one subcube query

is generated for each pane taking the two inner mea-

sures as inquired measures and all uninstantiated di-

mensions as inquired dimensions.

Query Generation for Zooming and Pivoting.

Zooming aggregated data needs to unfold new dimen-

sions. Every aggregated datum is decomposed into

multiple ones each of which corresponds to a dis-

tinct value of the dimension chosen for disaggrega-

tion. Therefore, only one subcube query is generated

for each such operation taking the chosen dimension

as the inquired dimension. Similarly, a pivoting oper-

ation is also transformed to one subcube query. How-

ever, zooming clustered data is different in that no ad-

ditional dimensions are required. When the user se-

lects one region of interest to zoom in, the system au-

tomatically computes the bounding box of the region.

MULTISCALE VISUALIZATION OF RELATIONAL DATABASES USING LAYERED ZOOM TREES AND

PARTIAL DATA CUBES

107

This bounding box is appended to the query corre-

sponding to the pane. The query will be processed

as usual except that query results will be ﬁltered us-

ing the bounding box and the ﬁltered results will be

re-clustered.

Subcube Query Translation. In our system, a sub-

cube query is ﬁrst translated into multiple point

queries before being further processed. The idea is

to replace all inquired dimensions in the query with

all possible combinations of their values. More pre-

cisely, if there are n inquired dimensions in the query

with cardinalityC

,...,C

respectively, it will be trans-

lated into

∏

i=0

point queries each of which maps to

a unique combination of values of these inquired di-

mensions. To minimize data transmission overhead,

the translation is performed by the CPU component

of the server.

6 SERVER-SIDE ALGORITHMS

In this section, we present algorithms developed for

the server.

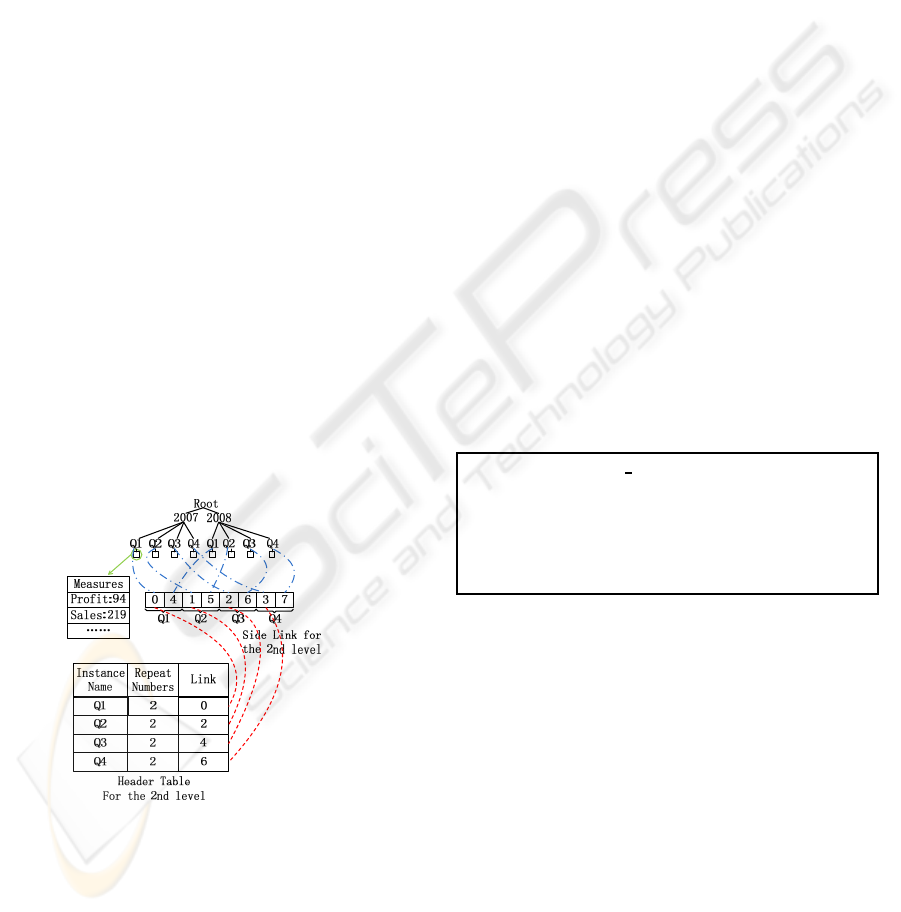
We adopt an H-tree to represent the partially ma-

terialized data cube on the server. H-tree is a hyper-

linked tree structure originally presented in (Han

et al., 2001), and was later deployed in (Han et al.,

2005) as the primary data structure for stream cubes.

However there are two major differences in our GPU-

Figure 5: GPU H-tree Structure.

based H-tree structure (Fig. 5) compared with the

original version. First, since CUDA does not sup-

port pointers, linked lists are replaced with arrays and

pointers are replaced with array indices. Second, the

array allocated for a side-link list is further divided

into contiguous segments each of which contains in-

dices of nodes which share the same attribute value.

We revised the structure of side links to achieve better

load balance and query performance.

Recently, GPUs attract more and more attentions

beyond the graphics community. Take the advantage

of the GPU H-tree structure, we develop a parallel

approach of online cubing algorithm to facilitate fast

query processing. We adopt NVidia CUDA (CUDA,

2008) as our programming environment. This is the

ﬁrst attempt to develop parallel cubing algorithms on

GPUs to the best of our knowledge.

6.1 Online Cubing

In this section, we only present the GPU-based par-

allel algorithm for point queries because a subcube

query can be easily translated into multiple point

queries. To achieve optimal performance, we propose

an approach exposing two levels of parallelism. Un-

like a sequential algorithm which processes queries

one by one, our algorithm can process thousands of

queries simultaneously in parallel. To further exploit

the massive parallelism of modern GPUs, we make

each query processed in parallel. We achieve this goal

by ﬁrst assigning one thread block to each query and

then making each thread in the block responsible for

an evenly divided portion of leaves or intermediate

nodes of the H-tree. Since each query is processed

by one thread block, we present the per-block query

processing algorithm as follows.

Algorithm: POINT QUERY

Input: HT, an H-tree;

pq, a point query including a set of instanti-

ated dimensions and a set of inquired measures;

Output: An aggregated value for each inquired

measure.

variables: i ← 0

begin

1. Follow the predeﬁned order of dimensions, locate

the last instantiated dimension, hd, in pq; load pq

and the header table for dimension hd into the shared

memory of the current thread block.

2. Search the header table for the i−th speciﬁed value

of hd in pq to retrieve the number of its repetitions,

rNum, and the index of its ﬁrst occurrence, start, in

the corresponding side-link list.

3. For each element e in the interval [start,start +

rNum] of this side-link list in parallel, locate the node

in the H-tree corresponding to e and use its parent in-

dex to move up the tree while checking all the instan-

tiated dimensions on the way. If one speciﬁed value of

every instantiated dimension can be found along the

path, fetch the values of the inquired measures stored

in the node corresponding to e and insert the value of

each inquired measure into a distinct temporary array.

IVAPP 2010 - International Conference on Information Visualization Theory and Applications

108

i+ = 1, go to step 2.

4. Perform parallel reduction on the temporary ar-

ray for each inquired measure to obtain the ﬁnal ag-

gregated value for each inquired measure.

end

In a real scenario, we initiate thousands of thread

blocks and each block takes care of one query. Note

that, in the ﬁrst step we assume that the entire header

table for hd and the query itself can be completely

loaded into the shared memory associated with the

block responsible for the query. Much care should be

taken to make sure it would not exceed the maximal

limit, which is 16KB per stream processor on G80.

If the cardinality of hd is relatively large, step 2 can

be parallelized as well. In step 3, we evenly divide

the rNum elements in the side-link list into chunks,

and the size of each chunk is rNum/S, where S is the

number of threads in a block. We allocate a tempo-

rary array for each inquired measure. Each element

in this array represents a partially aggregated value

computed from a particular chunk by the correspond-

ing thread. Since there could be more than one speci-

ﬁed values for the last instantiated dimension, we loop

over all these values and accumulate all partially ag-

gregated values to the temporary arrays. Finally, we

apply the parallel reduction primitive (Harris, 2008)

to each temporary array to compute the ﬁnal aggre-

gated value for each inquired measure.

The average time complexity of online cubing is

O(NM/(CP)) per point query, where P is the number

of processors allocated to process the query, N is the

number of tuples in the H-tree, M is the number of

dimensions, and C is the cardinality of the last instan-

tiated dimension in the query. The memory cost of

online cubing is O(S) per point query, where S is the

number of threads responsible for the query.

6.2 Online Clustering for Plot Charts

Implementing the zooming mechanism described in

Section 4.3.3 for plot charts requires performing clus-

tering in real time on the server. Classical clustering

methods such as K-means could be used for this pur-

pose. However, the main drawback of the k-means

algorithm in this scenario is that it requires multiple

iterations to cluster the data into a desired number of

clusters, which makes it hard to achieve real-time re-

sponse for large datasets even if we use its parallel

version (Shalom et al., 2008). Here we present a sim-

ple grid-based algorithm to cluster hundreds of thou-

sands of points into a desired number of clusters. In

doing do, we can not only reduce the overhead for

transferring a large amount of data but also can reduce

screen space clutter. To deliver optimal performance,

our clustering algorithm has been implemented on the

CPU of the server and is summarized in the following

steps.

1. Compute the bounding box of all input points.

2. Divide the bounding box into a 2D grid of N

bin

small boxes with equal size. Each small box

serves as a bucket.

3. Accumulate each point into an appropriate bucket

according to its screen space coordinates.

4. for every bucket in the grid, set the cluster center

of the bucket at the average location of the points

falling into the bucket.

This algorithm has a linear time and space com-

plexity. A reasonable value for N

bin

is 10. Users can

tune this parameter to achieve a visually pleasing pre-

sentation.

6.3 Performance

The described algorithms have been implemented and

tested on an Intel Core 2 Duo quad-core 2.4GHz pro-

cessor with an NVidia GeForce 8800 GTX GPU. To

cluster 1 millon randomly generated data points into

10x10 clusters, our grid-based clustering algorithm

only takes 22.96ms on a single core. The average

performance of the on-line cubing algorithm is pre-

sented in Fig. 6(a)&(b), where randomly generated

point queries are processed using an H-tree with 400k

and 800k tuples, respectively. Our GPU-based algo-

rithm can typically achieve a speedup much larger

than 10, and process 10,000 to 50,000 point queries

per second. The results also show that this algorithm

has more advantages when the number of dimensions

and the cardinality of each dimension are relatively

small. This is mainly because more dimensions and a

larger cardinality of the dimensions give rise to larger

H-trees which require more memory accesses. GPU

memory access latency is about 400-600 cycles which

is longer than CPU DRAM access latency.

6 9 12 15 18

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

# of dimension

Per Query Elapsed time(ms)

On Line Cubing Query for C160T800K

CPU

GPU

Speedup

20 40 80 160 320

Cardinality

Per Query Elapsed time(ms)

On Line Cubing for D15T400K

CPU

GPU

Speedup

(a) (b)

Figure 6: GPU speedup and average time vs. # of dimen-

sions and the cardinality of each dimension for online cub-

ing.

MULTISCALE VISUALIZATION OF RELATIONAL DATABASES USING LAYERED ZOOM TREES AND

PARTIAL DATA CUBES

109

7 USABILITY EVALUATION

To evaluate the usability of our system, we explored

several real datasets, including the American histor-

ical climate changes data of the last century and the

American census data in 2000 as well as the Coffee

Chain data(shown in the video). Since polaris can

be treated as the state-of-art for database visualiza-

tion, a user study was then conducted by comparing

the visualizations of these datasets using both zoom

tree and Tableau(Polaris). There were 8 total partici-

pants: 2 female,6 male. Their ages ranged from 19 -

28. They were from four different research labs, in-

cluding database(2), data mining(2), graphics(2) and

HCI(2).

7.1 Methods and Procedure

Before the testing, about one hour training and dis-

cussion were conducted in order to make them all

familiar with the meanings of datasets, the concepts

of cube as well as the interfaces of the two systems.

Participants were asked to perform two tasks with

both systems and rate(1-5) their satisfactions by ﬁll-

ing out questions. Note that, both tasks were in-

volved drilling down, rolling up and pivoting oper-

ations. An example step of one task is like: Se-

lect the sub-cube: ”Year=2007, Location=NewYork,

Product=Green Tea, then explore and ﬁnd the abnor-

mal relationships between the remaining dimensions

and the measure ’Proﬁt’ and then record them down.”.

An example of the questions is like: Rating the satis-

faction about the pivoting support along a zoom path.

7.2 Results and Observations

We measured the tasks times costed by each par-

ticipant. The average and variance time for task

one and two used by zoom tree are (average =

36s,variance = 15s) and (average = 95s,variance =

24s) respectively. While the corresponding results

used by polaris for the two tasks are (average =

45s,variance = 12s) and (average = 87s,variance =

26s) respectively. We also report the user satisfac-

tion ratings for the two different systems through ta-

ble 1. From the qualitative results including both pos-

itive and negative feedbacks, we found our system is

competitive with Polaris. Intuitive, easy to invoke and

manipulate, less clutter for high dimensional data all

make the layered zoom tree powerful. An interest-

ing observation is that most of the participants agree

table is good for overview visualization, but details

should be better visualized gradually in an isolated

layer to achieve clarity if focus and context is well

Table 1: User Satisfaction Ratings(0:Worst, 5:Best).

Question Zoom Tree Polaris

Subcube Selection 3.7 3.9

Pivoting 4.6 3.5

Aesthetic Appeal 3.4 3.7

Clutter Reduction 3.9 3.3

System Response Time 4.3 4.1

Historical Vis Support 3.8 3.7

processed. According to our experience, it’s really

hard to visualize datasets with 15 dimensions above

in a ﬁxed table using dimension embedding as in po-

laris, the higher the dimension the more clutter the

visualization. This is one of the main drawbacks of

polaris that layered zoom tree avoided. The results

also show that zoom tree gives quicker response time

for the same dataset, that’s mainly due to the leverage

of GPU parallelism through our H-tree online cubing

algorithm. Moreover, zoom tree only stores a partial

cube, compared with Polaris, it will save much more

spatial space. Flexibly changing the view is crucial

for users to facilitate the dynamic exploration, since

pivoting is not supported along the zoom path in po-

laris, layered zoom tree is absolutely the winner with

regard to this.

However, zoom tree also has some disadvantages,

for example participants think that although schema

based subcube selection is powerful, they prefer di-

rectly dragging and dropping dimensions to the table

shelves as in polaris. We also received some valu-

able suggestions for further improvement. For exam-

ple, one suggested to annotate the history button into

a meaningful thumbnail which reveals the structure of

the underlying subtree.

8 CONCLUSIONS

We have presented a visualization system with a

client-server architecture for multiscale visualization

of relational databases. Our system supports all types

of data cube operations using a combination of a

schema list, tables and zoom trees. To support fast

query processing on the server, we have also de-

veloped efﬁcient algorithms for online data cubing

and data clustering. The user study shows that our

proposed layered zoom tree and the overall system

framework are effective for visualizing databases.

Limitation. Our current system does not support

spatial dimensions such as maps. A spatial dimension

is likely to partition the screen space into irregularly

shaped regions instead of regularly shaped panes. In

future, we would be interested in investigating meth-

ods for placing charts inside such regions as well as

IVAPP 2010 - International Conference on Information Visualization Theory and Applications

110

zoom interfaces for spatial dimensions.

ACKNOWLEDGEMENTS

We would like to thank Shaowen Wang for the his-

torical climate dataset, Jiawei Han and Pat Han-

rahan for helpful discussions and suggestions, and

the anonymous reviewers for valuable comments.

This work was partially supported by NSF (IIS

09-14631), National Natural Science Foundation of

China (60728204/F020404).

REFERENCES

Proclarity analytics 6 2006. from: http://www.proclarity.

com/products/proclarity analytics 6.asp.

Report portal 2006:zero-footprint olap web client solution

xmla consluting. from:. http://www.reportportal.com.

Allison, W., Chris, O., Alexander, A., Michael, C., Vuk,

E., Mark, L., Mybrid, S., and Michael, S. (2001).

Datasplash: A direct manipulation environment for

programming semantic zoom visualizations of tabu-

lar data. Journal of Visual Languages & Computing,

12:551–571.

Antis, J., Eick, S., and Pyrce, J. (1996). Visualizing

the structure of large relational databases. Software,

IEEE, 13(1):72–79.

Bederson, B. B. and Hollan, J. D. (1994). Pad++: a zoom-

ing graphical interface for exploring alternate inter-

face physics. In UIST ’94: ACM symposium on user

interface software and technology.

Chaudhuri, S. and Dayal, U. (1997). An overview of

data warehousing and OLAP technology. SIGMOD

Record, 26:65–74.

CUDA (2008). Nvidia cuda (compute uniﬁed de-

vice architecture) programming guide 2.0.

http://developer.nvidia.com/object/cuda.html.

Ellis, G. and Dix, A. (2007). A taxonomy of clutter reduc-

tion for information visualisation. IEEE Transactions

on Visualization and Computer Graphics, 13(6).

Fua, Y.-H., Ward, M. O., and Rundensteiner, E. A. (1999).

Hierarchical parallel coordinates for exploration of

large datasets. In IEEE conference on Visualization

’99.

Gray, J., Chaudhuri, S., Bosworth, A., Layman, A., Re-

ichart, D., Venkatrao, M., Pellow, F., and Pirahesh, H.

(1997). Data cube: A relational aggregation operator

generalizing group-by, cross-tab and sub-totals. Data

Mining and Knowledge Discovery, 1:29–54.

Han, J., Chen, Y., Dong, G., Pei, J., Wah, B., Wang, J.,

and Cai, Y. (2005). Stream cube: An architecture

for multi-dimensional analysis of data streams. Dis-

tributed and Parallel Databases, 18(2):173–197.

Han, J., Pei, J., Dong, G., and Wang, K. (2001). Efﬁcient

computation of iceberg cubes with complex measures.

In SIGMOD.

Harris, M. (2008). Optimizing parallel reduction in cuda.

http://developer.download.nvidia.com/compute/cuda

/sdk/website/projects/reduction/doc/reduction.pdf.

Inc, B. (2007). Microsoft Excel 2007 Charts & Tables Quick

Reference Guide.

Kesaraporn, T., Amitava, D., and Robyn, O. (2004). Hddv:

Hierarchical dynamic dimensional visualization for

multidimensional data. In IASTED ’2004: Inter-

national Conference on Databases and Applications,

pages 157–162.

Kreuseler, M. and Schumann, H. (1999). Information vi-

sualization using a new focus+context technique in

combination with dynamic clustering of information

space. In NPIVM ’99: the 1999 workshop on new

paradigms in information visualization and manipu-

lation.

Maniatis, A. S., Vassiliadis, P., Skiadopoulos, S., and Vas-

siliou, Y. (2003). Advanced visualization for olap.

In DOLAP ’03: 6th ACM international workshop on

Data warehousing and OLAP.

Mansmann, S. and Scholl, M. H. (2007). Exploring olap

aggregates with hierarchical visualization techniques.

In SAC ’07: ACM symposium on Applied computing.

Peng, W., Ward, M. O., and Rundensteiner, E. A. (2004).

Clutter reduction in multi-dimensional data visualiza-

tion using dimension reordering. In INFOVIS ’04:

Proceedings of the IEEE Symposium on Information

Visualization.

Rao, R. and Card, S. K. (1994). The table lens: merging

graphical and symbolic representations in an interac-

tive focus + context visualization for tabular informa-

tion. In CHI ’94: SIGCHI conference on Human fac-

tors in computing systems.

Rundensteiner, E. A., Ward, M. O., Yang, J., and Doshi,

P. R. (2002). Xmdvtool: visual interactive data explo-

ration and trend discovery of high-dimensional data

sets. In SIGMOD ’02: 2002 ACM SIGMOD interna-

tional conference on Management of data.

Shalom, S. A., Dash, M., and Tue, M. (2008). Efﬁcient

k-means clustering using accelerated graphics proces-

sors. In DaWaK ’08: 10th international conference on

Data Warehousing and Knowledge Discovery.

Stolte, C., Tang, D., and Hanrahan, P. (2002). Polaris: A

system for query, analysis, and visualization of multi-

dimensional relational databases. IEEE Trans. on Vi-

sualization and Computer Graphics, 8:52–65.

Stolte, C., Tang, D., and Hanrahan, P. (2003). Multiscale

visualization using data cubes. IEEE Trans. on Visu-

alization and Computer Graphics, 9:176–187.

Techapichetvanich, K. and Datta, A. (2005). Interactive vi-

sualization for olap. In ICCSA ’2005: International

Conference on Computational Science and its Appli-

cations Part III, pages 206–214.

Weijia Xu, K. P. (2008). On interactive visualization with

relational database. In InfoVis’2008, Poster.

MULTISCALE VISUALIZATION OF RELATIONAL DATABASES USING LAYERED ZOOM TREES AND

PARTIAL DATA CUBES

111