GRAPH MATCHING USING SIFT DESCRIPTORS

An Application to Pose Recovery of a Mobile Robot

Gerard Sanrom`a

, Ren´e Alqu´ezar

and Francesc Serratosa

Departament d’Enginyeria Inform`atica i Matem`atiques, URV

Av. Paisos Catalans 26, Campus Sescelades, 43007 Tarragona, Spain

Institut de Rob`otica i Inform`atica Industrial, CSIC-UPC

Llorens Artigas 4-6, 08028 Barcelona, Spain

Keywords:

Graph matching, SIFT, Pose recovery.

Abstract:

Image-feature matching based on Local Invariant Feature Extraction (LIFE) methods has proven to be suc-

cessful, and SIFT is one of the most effective. SIFT matching uses only local texture information to compute

the correspondences. A number of approaches have been presented aimed at enhancing the image-features

matches computed using only local information such as SIFT. What most of these approaches have in com-

mon is that they use a higher level information such as spatial arrangement of the feature points to reject a

subset of outliers. The main limitation of the outlier rejectors is that they are not able to enhance the conﬁg-

uration of matches by adding new useful ones. In the present work we propose a graph matching algorithm

aimed not only at rejecting erroneous matches but also at selecting additional useful ones. We use both the

graph structure to encode the geometrical information and the SIFT descriptors in the node’s attributes to pro-

vide local texture information. This algorithm is an ensemble of successful ideas previously reported by other

researchers. We demonstrate the effectiveness of our algorithm in a pose recovery application.

1 INTRODUCTION

Visual odometry is used in mobile robotics to measure

the spatial displacement experienced by a robot given

the images taken at each location. In many SLAM

systems it is a key point to estimate the robot trajec-

tory in open-loop (V. Ila and Andrade-Cetto, 2009),

(V. Ila and Sanfeliu, 2007), (Ila et al., 2010).

A data association between the images is needed

in order to estimate the spatial displacement of the

robot. Image feature matching based on local invari-

ant features extraction (LIFE) has proven to be suc-

cessful, and SIFT (Lowe, 2004) is one of the most

effective. In SIFT, each feature is represented by its

location and orientation on the image and a descriptor

vector retaining information relative to the local tex-

ture. Such descriptors are invariant at a certain extent

to changes in scale, rotation and illumination, mak-

ing them suitable for matching images from the same

scene under varying pose and environmental condi-

tions. Features are then associated according to the

closeness between their descriptors.

There exist a number of approaches aimed at

enhancing the data association computed using lo-

cal descriptors. Some examples are ICP (Besl and

McKay, 1992), RANSAC (Brown and Lowe, 2003)

and Graph Transformation Matching (Aguilar et al.,

2009). What all these approaches have in common is

that they use the geometrical information to reject a

subset of erroneous matches (outliers).

Graphs are general-purpose structures aimed at

representation where features are represented by

nodes and the relations between them by edges. More

in the topic of the present paper, Aguilar et al.

(Aguilar et al., 2009) have recently presented an ap-

proach to use graph-based representations to the same

end. To give some details, they build two K-nearest-

neighbour graphs with the keypoints of the two im-

ages that have been matched (i.e., edges are placed

joining a keypoint with the K nearest neighbours in

space). The non-matched keypoints are discarded so,

they begin with two isomorphic graphs. At each itera-

tion, the algorithm removes the pair of matched nodes

most structurally dissimilar and re-computes the K-nn

structure (in both graphs). The process ends when two

topologically identical graphs are obtained. Graph

Transformation Matching has been recently used for

recoverying the pose of a mobile robot from a set

249

Sanromà G., Alquézar R. and Serratosa F. (2010).

GRAPH MATCHING USING SIFT DESCRIPTORS - An Application to Pose Recovery of a Mobile Robot.

In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 249-254

DOI: 10.5220/0002829702490254

 SciTePress

of known 2D views using epipolar geometry (Frank-

Bolton et al., 2008).

The main limitation of the outlier rejectors is that

they are unable to produce additional useful matches

different from the initial set.

In this paper we present a novel iterative graph

matching algorithm aimed at evolving an initial set

of correspondences computed with the locally based

SIFT method, to a kind of compromise between the

constraints imposed by both the SIFT descriptors and

the structural relations. Unlike the approaches de-

scribed above, our method is able of including addi-

tional useful matches (those that satisfy the new com-

bined constraints). This is the ﬁrst graph matching

algorithm that we have knowledge using structural re-

lations along with SIFT descriptors.

We demonstrate the effectiveness of our method

in a pose recovery application. Our method gets less

error with more matches.

The organization of this paper is as follows: In

section 2 we introduce some preliminary concepts. In

section 3 our graph matching algorithm is presented.

In section 4 we describe the experiments discuss the

results, and in section 5 the conclusions are given.

2 PRELIMINARIES

Deﬁnition 1. A Graph G (attributed relational

graph) is a 3-tuple G = (V,E,Z) where V is a set

of vertices (also called nodes), E ⊆ V × V is a set

of edges, where e ∈ E, e = (v

) is an edge joining

nodes v

∈ V, and Z is a set of vectors, where z

∈ Z

is a vector of attributes associated to node v

∈ V.

Although edges may contain attributes, we focus

on the binary case where edges exist (1) or not (0).

Deﬁnition 2. A matching matrix S is a binary

matrix deﬁning an injective mapping from a data-

graph G

= (V

) to a model-graph G

). Hence, an element s

∈ S is set to 1

if node v

∈ V

is matched to node v

∈ V

, and 0 oth-

erwise. On the other hand, matching node v

∈ G

node NULL (no node) means to put the a-th row of S

to zeros.

A number of SIFT keys are extracted from an

image through the local invariant feature extraction

method described in (Lowe, 2004).

Deﬁnition 3. Each SIFT key P





is composed by its 2D location in the image X

), its gradient magnitude and orientation R

,α

) and a descriptor vector of length 128, U

i,1

,... ,u

i,128

) with information the local texture on

the image.

Let P

,i = 1,... ,n and P

, j = 1,... ,m be the

SIFT keys of a source and destination images, respec-

tively.

Deﬁnition 4. A SIFT key P

from the source im-

age is positively SIFT matched to a SIFT key

from the destination image if dist





min



dist





, j = 1,. ..,m and

dist

(

)

dist

(

)

ρ, where dist(•) is the Euclidean distance, U

is the

descriptor of the destination image with the second

smallest distance from U

, and 0 < ρ ≤ 1 is a ratio

value controlling the tolerance to false positives.

Let P

left

,i = 1, ..., n and P

right

, j = 1,... ,m be the

SIFT keys of a left and right images of a scene, ob-

tained with stereo-vision. Let f be a function such

that, f (i) = j means that P

left

is positively SIFT

matched to P

right

, and f (i

′

) = 0 means that P

left

′

is not

matched to any. Let X

= (x

)

, l = 1, ...,t,

be the 3D coordinate-vectors obtained through stereo

triangulation of the local 2D coordinate-vectors X

left

and X

right

f(k)

, ∀k s.t. f(k) 6= 0.

Deﬁnition 5. A K-nearest-neighbour (K-nn) SIFT

graph G is a 3-tuple G = (V,E,Z), where V

is a set of nodes associated to each X

, Z =

left

| f(k) 6= 0

, is a set of SIFT descriptor-

vectors associated to the nodes, and E is a set of edges

where for each v

there is an edge (v

) that join v

with its K closest neighbours v

, p = 1.. .K in the

space of the coordinate-vectors X

3 A NOVEL GRAPH MATCHING

ALGORITHM

Let G

= (V

) and G

= (V

) be a

data and a model graph, respectively. In this sec-

tion, we present an iterative graph matching algo-

rithm, aimed at driving an initial estimate of the best

matching matrix S

(1)

through the space of matching

conﬁgurations, in the direction ﬁxed by a new set of

constraints aimed at representing a compromise be-

tween SIFT attributes and structural relations. This

algorithm is built from an ensemble of previously re-

ported ideas by other researchers (Gold and Rangara-

jan, 1996) (Luo and Hancock, 2001) (Cross and Han-

cock, 1998).

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

250

3.1 A Measure of Structural

Consistency

It is a well-known strategy to state that a match from

a node v

∈ V

to a node v

∈ V

is more likely to

occur as more nodes adjacent to v

are assigned to

nodes adjacent to v

(Luo and Hancock, 2001) (Gold

and Rangarajan, 1996).

We deﬁne a hit as a node v

∈ V

adjacent to v

that is matched to a node v

∈ V

adjacent to v

(Luo and Hancock, 2001) used the EM algorithm

to iteratively ﬁnd the maximum likelihood estimate

of the matching matrix S. They used a probability

model based on the Bernoulli distribution in order to

accomodate hits and no hits with ﬁxed probabilities

(1− P

) and P

(being P

the probability of error).

On the other hand, (Gold and Rangarajan, 1996)

proposed an iterative algorithm to solve the assign-

ment problem using graduated nonconvexity. They

used the compatibility measure between links to

gauge the hits.

Interestingly, both approaches (Luo and Hancock,

2001) and (Gold and Rangarajan, 1996) according

with their respective frameworks (i.e., Expectation-

Maximization and graduated nonconvexity) ended up

maximizing a similar expression.

We adopt the mentioned expression as our mea-

sure of structural consistency for the match v

→ v

This expression is

aα

= exp

∑

b∈V

∑

β∈V

αβ

bβ

(1)

where D and M are the adjacency matrices of G

and

, respectively (i.e., D

means that there is an edge

joining v

and v

; and M

αβ

means that there is an edge

joining v

and v

), s

bβ

∈ S is an element of the n ×

m current matching matrix S and µ > 0 is a control

parameter.

The presented expression is the exponential of the

number of hits for a match a → α, weighted by a pa-

rameter µ.

In (Gold and Rangarajan, 1996), µ controls the

convexity to avoid poor local minima. A high value

of µ tends to exaggerate the difference of the highest

values with respect to the others. On the other hand,

in (Luo and Hancock, 2001), µ = ln[(1− P

)/P

]. A

high value of P

means not to penalize too much the

structural errors. This has sense, since increasing the

value of P

(decreasing the value of µ) has the effect

of smoothing the differences among the values.

3.2 A Measure of Similarity between

SIFT Attributes

Up to this point, we have shown how to measure the

contribution of matching one node to another with re-

gards to the structural relations.

We propose the inverse of the distance as the mea-

sure of similarity of the SIFT attributes from two

nodes. More formally, we deﬁne the similarity of

matching node v

∈ V

to node v

∈ V

with regards

to the SIFT attributes as

aα

dist(z

)

(2)

where dist





is the Euclidean distance between

SIFT descriptors z

∈ Z

and z

∈ Z

The advantages of this measure are that we can

easily reformulate the ratio criterion of deﬁnition 4

so as to obtain the same results as the original SIFT

matching, while having turned a distance to a similar-

ity function.

3.3 A Combined Measure of

Consistency and Similarity

We propose a combined measure of the consistence

of a match inspired in the work of simultaneous

graph matching and alignment by Cross and Hancock

(Cross and Hancock, 1998). In their work, they com-

bined the structural relations with attributes informa-

tion of the 2D coordinate positions to recover both

the conﬁguration of matches and the spatial transfor-

mation. Since the SIFT descriptors have a constant

value throughout the process, we are only interested

in recovering the correspondences.

Our combined expression for gauging the consis-

tence of matching the node v

∈ V

to node v

∈ V

is:

aα

= Q

aα

(3)

where Q

aα

is the structural consistency coefﬁcient de-

scribed in equation (1) and R

aα

is the SIFT similarity

coefﬁcient described in equation (2).

The use of the multiplication to combine the mea-

sures due to both the local information and the sur-

rounding matches is closely related to the idea of

Probabilistic Relaxation (R.A. and W., 1983).

With this measure to hand, we deﬁne the matrix Ω

of combined coefﬁcients as:

Ω =







... W

. W

aα

... W







(4)

GRAPH MATCHING USING SIFT DESCRIPTORS - An Application to Pose Recovery of a Mobile Robot

251

3.4 A Cleaning Heuristic

A cleaning heuristic is needed to obtain a binary

n × m matching matrix (deﬁnition 2) S that selects

the matches corresponding to the highest coefﬁcients

from the continuous matrix Ω. Since it may not ex-

ist an exact isomorphism between two graphs G

and

, we also need a criterion to match nodes v

∈ G

to NULL.

Borrowing the idea of the ratio criterion of the

positive SIFT matches, we propose the following

cleaning procedure:

1. Initialize S to an n× m matrix of zeros. Let Ω

′

Ω. Set all W

′

a,α

∈ Ω

′

to zero except those W

′

a,k

from each row a of Ω

′

s.t. W

′

a,k

= max



′

a,α



α = 1,.. .,m and W

′

a,k

′

a,k2

, where W

′

a,k2

the second highest element in the a-th row of Ω

′

Note that we use the same ratio value 0 ≤ ρ ≤ 1

as in deﬁnition 4 to control the acceptance rate.

2. Find the maximun element W

′

a,α

∈ Ω

′

and activate

the corresponding match s

aα

∈ S

3. Set to zeros the row and column of Ω

′

where W

′

a,α

belongs to

4. Repeat steps 2-3 until Ω

′

becomes a matrix of ze-

ros

3.5 The Algorithm

Let G

and G

be two K-nn SIFT graphs obtained

from two pairs of stereo-images, with n and m nodes

respectively.

Our algorithm for matching G

to G

is the fol-

lowing:

1. Initialize the matching matrix at the ﬁrst itera-

tion S

(1)

to be the result of applying the cleaning

heuristic of subsection 3.4 to the matrix of SIFT

similarity coefﬁcients computed using equation

(2). Note that the structural information has no

inﬂuence in the computation of the initial match-

ing matrix, and that it becomes an injective set of

positive SIFT matches.

2. At iteration i, compute the n × m matrix of com-

bined coefﬁcients Ω

(i)

as described in equations

(3) and (4)

3. Compute the n× m matching matrix S

(i+1)

apply-

ing to Ω

(i)

the cleaning heuristic described in sub-

section 3.4

4. Increment the iteration number i and repeat steps

2-4 until convergence of the matching matrix

In the next section we give further details about

the empirical behaviour shown by the present algo-

rithm with regards to the convergence.

4 EXPERIMENTS AND

DISCUSSION

We have designed a pose recoveryexperiment to eval-

uate the effectivenes of three image-featuresmatching

methods. The errors obtained estimating the displace-

ment of the robot using the matches selected by each

method are taken as a measure of effectiveness of the

method.

We have 130 stereo-image pairs taken at differ-

ent places during a mobile robot outdoor route. We

have the ground truth positions and orientations of

the robot at these places, computed with high preci-

sion using the SLAM system presented in (Ila et al.,

2010), (V. Ila and Andrade-Cetto, 2009). These 130

images are divided into two sets, the origin set and

the destination set, with 65 images each, so that one

image of the origin set is matched against one image

of the destination set (thus, we carry out 65 matching

experiments).

To summarize, for each experiment we have two

pairs of stereo-images (origin and destination) each

one with its set of SIFT keys (features). Each fea-

ture is associated to a 3D coordinate position (through

stereo-triangulation), relative to the camera of the

robot at that place. We also have the ground truth

positions and orientations of each place.

Given an association between the features at the

origin and destination places, we make an estimation

of the destination pose (position and orientation), as

described in (V. Ila and Sanfeliu, 2007).

We assume that the higher the error between the

estimated and the ground truth destination poses is,

the worse the features association is.

We have compared the approach presented in this

paper (denoted as Graph Matching with SIFT) to

SIFT matching (deﬁnition 4) (Lowe, 2004) and Graph

Transformation Matching (Aguilar et al., 2009).

We have used a maximum of 80 features in each

experiment when available. This has represented

around a 50% of the total available data. The features

have been selected among the most salient (regarding

the gradient magnitude of the SIFT keys). We have

built a K-nn SIFT graph (deﬁnition 5) for each pair of

stereo-images using the values of K = 7 in the Graph

Transformation Matching method and K = 21 in our

method. The value of µ = 0.15 from equation (1) has

been used in our method (the values used in all the

methods have been carefully chosen to perform well).

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

252

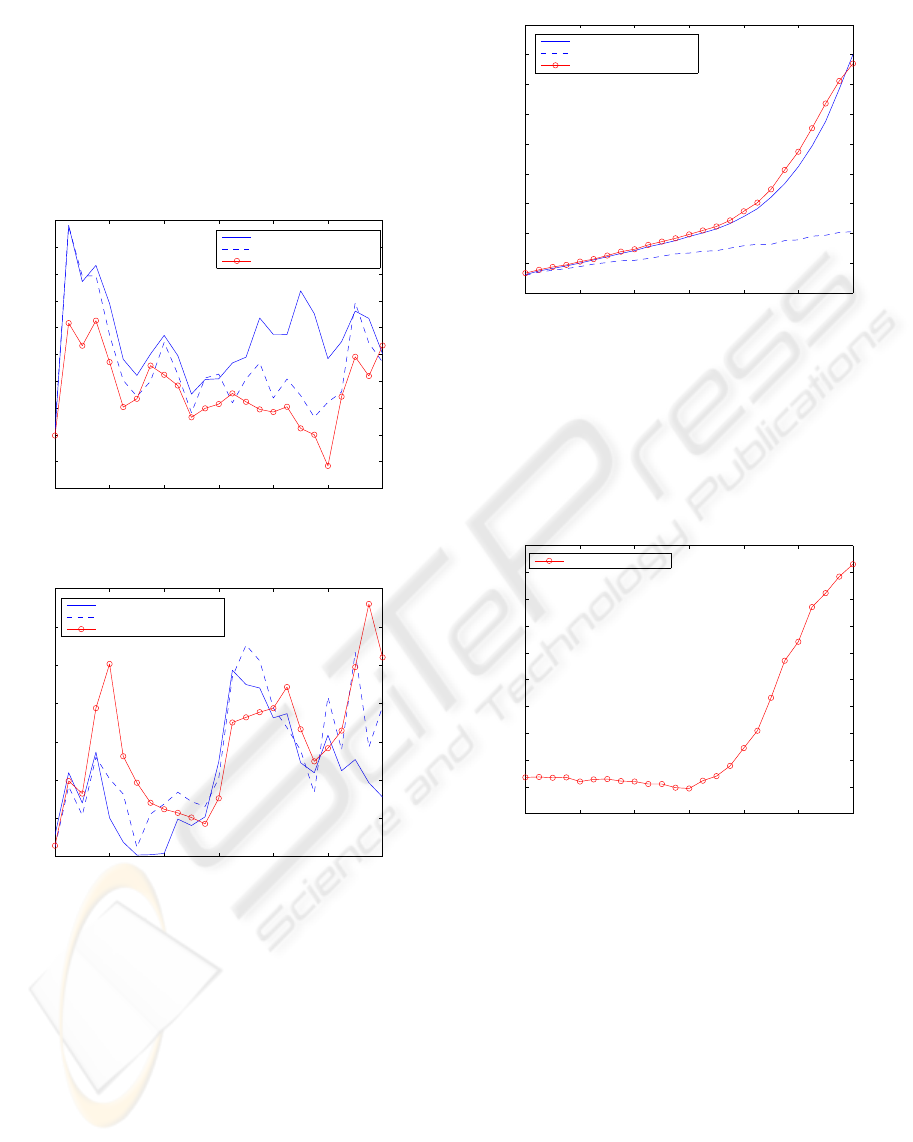
Figures 1 and 2 show the mean errors among

the 65 experiments of each method at an interval of

matching acceptance ratios ranging from 0.4 to 1. Al-

though lower ratio values often lead to less error (bet-

ter quality matches), the analysis at values lower than

0.4 has not too much interest, since a signiﬁcant num-

ber of matching experiments return not enough (or not

at all) results to recover the spatial transformations.

0.4 0.5 0.6 0.7 0.8 0.9 1

10.5

11.5

12.5

13.5

14.5

ratio

Position error (meters)

Position error wrt the ratio

SIFT Matching

Graph Transformation Matching

Graph Matching with SIFT

Figure 1: Position errors w.r.t. the acceptance ratio.

0.4 0.5 0.6 0.7 0.8 0.9 1

0.2

0.25

0.3

0.35

0.4

0.45

0.5

0.55

ratio

Angle (radians)

Orientation error wrt the ratio

SIFT Matching

Graph Transformation Matching

Graph Matching with SIFT

Figure 2: Orientation errors w.r.t. the acceptance ratio.

Figure 3 shows the mean number of matches re-

turned by each method at each acceptance ratio.

We have empirically observed two different be-

haviours with regards to the convergence of the

present algorithm. The stable case, where the match-

ing matrix reaches a certain conﬁguration that re-

mains stable along iterations. In this case, we stop

our algorithm at the ﬁrst iteration where the matching

matrix does not change. The unstable case, where the

matching matrix evolves until a point where it starts

to loop indeﬁnitely between two different conﬁgura-

tions. In this case, we stop our algorithm and we

arbitrarily choose one of both conﬁgurations as we

consider that they are equally likely solutions. Both

0.4 0.5 0.6 0.7 0.8 0.9 1

ratio

Number of matchings

Number of matchings wrt the ratio

SIFT Matching

Graph Transformation Matching

Graph Matching with SIFT

Figure 3: Number of matches returned w.r.t. the acceptance

ratio.

cases are observed nearly in the same number of ex-

periments. Figure 4 represents the mean number of it-

erations needed by our method to stop (regarding the

mentioned criteria). The maximum number of itera-

tions permitted is 20.

0.4 0.5 0.6 0.7 0.8 0.9 1

ratio

number of iterations

Number of iterations of the Graph Matching with SIFT algorithm wrt the ratio

Graph Matching with SIFT

Figure 4: Number of iterations until stop.

As is shown in ﬁgure 1, the proposed approach

demonstrates to perform signiﬁcantly better than the

others with regards to the position estimation, in the

database used in this experiment. On the other hand,

as we see in ﬁgure 2, orientation errors are not as good

as it would be expected. It is worth noting that the

Graph Transformation Matching method also experi-

ments a performance decreasing with respect to SIFT

matching in orientation recovery. We need to further

study this fact, since both approaches are aimed at the

improvement of the SIFT matching. Figure 3 show

evidences that our method is not only supposed to re-

move outliers, but also to introduce additional use-

ful matches. It can be observed that, while the pos-

itive SIFT matches added above an acceptance ratio

of 0.65 (≈ 7 matches) do nothing but to deteriorate

GRAPH MATCHING USING SIFT DESCRIPTORS - An Application to Pose Recovery of a Mobile Robot

253

its efﬁciency, our method improves its efﬁciency until

a threshold of 0.9 (≈ 24 matches), where it actually

performs optimally. On the other hand, it is clear that

the enhancement introduced by the Graph Transfor-

mation Matching is, as expected, based on the rejec-

tion of the SIFT outliers.

5 CONCLUSIONS

We have presented a new attributed graph matching

algorithm that combines the local texture information

of the SIFT descriptors with the higher level informa-

tion of the graph structure to derive a set of matches.

Unlike the SIFT enhancements based on outlier rejec-

tion, our approach aims to both eliminate erroneous

matches and add new useful ones. We have evaluated

three different approaches to image-feature matching

in a pose recovery application: our method, SIFT

matching (Lowe, 2004), and a graph-based outlier re-

jector run on the positive SIFT matches (Aguilar et al.,

2009). In the methods that use graphs, we have used

the 3-Dimensional positional information attached to

each feature to build the K-nn SIFT graphs.

In the position estimation experiments, our ap-

proach has been superior than the others. With a

higher number of correspondences than SIFT match-

ing, our method gets even a lower positional error

than the outlier rejector. In conclusion, our method

gets more and better matches.

On the other hand, both our method and the outlier

rejector perform worse than SIFT matching in orien-

tation recovery. This seems contradictory since both

methods are designed as an enhancement of SIFT

matching. We therefore need to further study this fact.

ACKNOWLEDGEMENTS

We want to acknowledge Juan Andrade-Cetto and

Viorela Ila for providing us with the stereo images

from the robot route, the code for triangulating the

3D feature positions and the ground truth poses used

to compute the errors.

This research was partially supported by Con-

solider Ingenio 2010, project CSD2007-00018, by the

CICYT project DPI 2007-61452 and by the Universi-

tat Rovira i Virgili.

REFERENCES

Aguilar, W., Frauel, Y., Escolano, F., and Martinez-Perez,

M. E. (2009). A robust graph transformation match-

ing for non-rigid registration. Image and Vision Com-

puting, 27:897–910.

Besl, P. J. and McKay, N. D. (1992). A method for regis-

tration of 3-d shapes. IEEE Transactions on Pattern

Analysis and Machine Intelligence, 14(2).

Brown, M. and Lowe, D. G. (2003). Recognising panora-

mas. Proceedings of the International Conference on

Computer Vision.

Cross, A. D. J. and Hancock, E. R. (1998). Graph matching

with a dual-step em algorithm. IEEE Transactions on

Pattern Analysis and Machine Intelligence, 20(11).

Frank-Bolton, P., Alvarado-Gonzalez, A. M., Aguilar, W.,

and Frauel, Y. (2008). Vision based localization for

mobile robots using a set of known views. In Pro-

ceedings of Advances in Visual Computing (LNCS),

volume 5358 of 4th International Symposium on Vi-

sual Computing, pages 195–204.

Gold, S. and Rangarajan, A. (1996). A graduated assign-

ment algorithm for graph matching. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

18(4).

Ila, V., Porta, J. M., and Andrade-Cetto, J. (2010).

Information-based compact pose slam. IEEE Trans-

actions on Robotics, 26(1). In press.

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. International Journal of Com-

puter Vision, 60(2).

Luo, B. and Hancock, E. R. (2001). Structural graph match-

ing using the em algorithm and singular value decom-

position. IEEE Transactions on Pattern Analysis and

Machine Intelligence, 23(10).

R.A., H. and W., Z. S. (1983). On the foundations of re-

laxation labeling proecesses. IEEE Transactions on

Pattern Analysis and Machine Intelligence, 5(3).

V. Ila, J. P. and Andrade-Cetto, J. (2009). Reduced state

representation in delayed state slam. In Proceedings of

the IEEE/RSJ International Conference on Intelligent

Robots and Systems, Saint Louis, pages 4919–4924.

V. Ila, J. Andrade-Cetto, R. V. and Sanfeliu, A. (2007).

Vision-basedloop closing for delayed state robot map-

ping. In Proceedings of the IEEE/RSJ International

Conference on Intelligent Robots and Systems, San

Diego.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

254