CONSTRUCTING THE HYBRID DITHERING MATRIX WITH

EQUAL CLUSTERED DOT DENSITY

Xu Guoliang and Tan Qingping

Computer College, National University of Defense Science and Technolgy, Changsha Hunan, China

Keywords: Image Halftone, Dithering Matrix, Geometry Subdivision, Delaunay Triangulation, PSNR.

Abstract: Hybrid halftone has great strengths over amplitude and frequency modulated halftone in offset printing.

Modern CTP systems employ hybrid dithering algorithm, because dithering algorithm is a very efficient

halftone algorithm. The shapes, distribution and density of clustered dots in halftone images depend on

hybrid dithering matrix. This research proposes a new method to construct a hybrid dithering matrix with

equal clustered dot density, based on a new geometry subdivision derived from Delaunay Triangulation.

The matrix helps increase clustered dot density and maintain constraints of the offset printing procedure.

This paper also discusses the uniformity of expanded central point set and quality of quadrilaterals of the

geometry subdivision by comparing PSNR and quality factor value with that of the previous work.

1 INTRODUCTION

Halftone images are classified into three categories

in terms of dot shape and distribution: AM, FM and

Hybrid halftone images. (1) Amplitude Modulated

(AM) halftone uses different size of clustered dots to

represent different grey values. Each clustered dot

belongs to a dot unit tiled in the halftone plane. It is

better if the percentage of black pixels in the dot unit

equals to the average grey value of the pixels in the

same location of the continuous tone image. AM

halftone is often used in laser printer, laser copier

and traditional offset printing. (2) Frequency

Modulated (FM) halftone randomly distributes dots

(pixels) of output device and uses dot density to

represent grey value. Dot density is defined as the

number of dots in a unit area. The dot density of FM

halftone is usually much higher than that of AM

halftone. High dot density will make a smooth edge

for line works and fine patterns. FM halftone fits for

high resolution devices, such as ink jet printer. (3)

Hybrid halftone dots vary both in size and density of

clustered dots to represent different grey values. It

combines the advantages of both AM and FM

halftone and is widely used in CTP (Computer to

Plate) systems.

In most cases, all halftone algorithms are often

described as the following three computing

procedures: point procedure, neighbouring point

procedure and iteration procedure. Algorithm of

point procedure is very simple and highly efficient

in speed. One typical point procedure, dithering

algorithm, requires a dithering matrix that will be

tiled in halftone plane. When a dithering algorithm

halftones a continuous tone image, it first compares

the value of the pixels of continuous tone image with

the element values of dithering matrix in the

corresponding position. Then, it sets the halftone

pixel to “0” or “1”, if the pixel value of the

continuous tone image is greater or less than the

value of the element of the matrix. Halftoning with

dithering matrix is often referred to as screening.

This research originates from the observation of

the unbalanced clustered dot densities shown in

Figure 1 and Figure 2 together. It is a vital issue for

hybrid halftone to maximize dot density in halftone

image and maintain the constraints of offset printing

procedure. There are two constraints of offset

printing procedure: (1) a minimum clustered dot size

that could be reliably reproduced in print; (2) a

standard dot gain curve of offset printing. The

positive clustered dot size in the light region and the

negative clustered dot size in the shadow are small,

when the clustered dot density is high. Therefore, we

balance the dot density in the highlight and shadow

of hybrid halftone image at all grey levels in order to

maximize the clustered dot density.

The main contributions of this research are: (1)

propose a new geometry subdivision of the halftone

plane, of which all the faces (or regions) are quadri-

Guoliang X. and Qingping T. (2010).

CONSTRUCTING THE HYBRID DITHERING MATRIX WITH EQUAL CLUSTERED DOT DENSITY.

In Proceedings of the International Conference on Imaging Theory and Applications and International Conference on Information Visualization Theory

and Applications, pages 61-67

DOI: 10.5220/0002830400610067

 SciTePress



7 clustered dots

Figure 1: Detail of

highlight.

13 clustered dots

Figure 2: Detail of

shadow.

laterals. The subdivision is constructed with points

of a expanded central points set as a vertex set; (2)

evaluate the quality of quadrilaterals in the proposed

geometry subdivision in this research; (3) analyze

the uniformity of the expanded central point set by

comparing PSNR of the initial central point sets; (4)

construct a dithering matrix with equal clustered dot

density.

2 RELATED WORK

A lot of research concerning hybrid screening has

been conducted since the 1990s. Screening is a

technique to halftone continuous tone images with

dithering algorithms. Printing industry usually uses

screening technology in desk top printers, ink jet

printers and RIPs (Raster Image Processor) for

printing industry.

Barco first launched its hybrid screening product

SAMBA for flexo printing. It combines AM and FM

halftone in a single screening process. It halftones

continuous tone images with FM halftone in tint

under 10% and above 90%. It halftones continuous

tone images with AM halftone in tint between 10%

and 90%. So, it has the merits of FM halftone, for

instance, fine detail of FM in the highlight instead of

the demerits of FM halftone, for instance, excessive

dot gain of FM in the middle tone.

Other companies, like Founder Electronic and

Dainippon Screen, issued their hybrid screening

products such as FAM and Spekta. However, few

papers have been published on the design of these

products.

Among the academic researches related to

halftone technology, Ulichney first proposed the

blue noise model for FM halftone (Ulichney, 1988).

According to Ulichney’s theory, the ideal halftone

image distributes the same-sized dots as

homogeneously as possible. By doing so, the

spectral content of the image is composed entirely of

high-frequency spectral components. And as blue is

the high-frequency component to visible white light,

it is named blue noise model. However, blue noise

model does not work for some printing procedures

such as offset printing, because separate pixels can

not be reproduced reliably. Hybrid screen is applied

in offset printing instead of FM screen.

Later, Lau formalized the concept of green noise

model for hybrid screen and proposed an algorithm,

EDODF (Error Diffusion with Output-Dependent

Feedback), to design such screens based on

enforcing certain spatial-statistical characteristics of

green noise (Lau et al, 1998; Lau et al, 2000).

However, it is very difficult to control the shape of

clustered dot with his method (see Figure 3).

Figure 3: Sample image halftoned by EDODF algorithm.

Damera-Venkata and Lin used the void-and-

cluster algorithm with a donut filter to create green

noise screens (Damera-Venkata and Lin,2004).

Ostromoukhov proposed a hybrid screen design

method based on stochastic seeding and Delaunay

triangulation (Ostromoukhov and Hersch,1999

This method apparently has the strength to control

the shape of the clustered dots. Tu tried other ways

of filling tint in the Delaunay triangulation (Tu et al,

2000). The clustered dot densities in highlight and

shadow have big difference for the result of research

in (Ostromoukhov and Hersch,1999; Tu et al, 2000),

as illustrated in Figure 1 and Figure 2.

Xu proposed two theorems to guide the

optimization of the geometry subdivision from

Delaunay triangulation, with which a dithering

matrix with balanced clustered dot densities were

constructed (

Xu and Tan, 2009). We will elaborate on

these theorems in Section 3.

IMAGAPP 2010 - International Conference on Imaging Theory and Applications

3 GEOMETRY THEORY FOR

OPTIMIZING HYBRID

DITHERING MATRIX

In the existing research, constructing hybrid

dithering matrix based on a geometry subdivision

usually follows this procedure (Ostromoukhov and

Hersch,1999; Tu et al, 2000): (1) randomly

distribute some dots in a tile unit of a halftone plane

as the vertex of geometry subdivision; (2) calculate a

geometry subdivision to a tile unit of the halftone

plane with the above central points as the vertex of

the subdivision; (3) produce the dithering matrix by

filling grey gradient tint in the regions of the

subdivision above and make the vertex of the

subdivision the darkest point and the centre of the

region as the lightest point. Then, the grey mode

image filled is converted directly to a dithering

matrix by taking the pixel value of the image as the

value of element of the matrix in the corresponding

position. The requirements for the geometry

subdivision are: (1) The narrow shape of region

should be avoided to make the shape of clustered dot

favourable in printing; (2) The vertex’s number is

expected to be as close as to the region’s number of

the subdivision. It is the best case as a result of

balancing clustered dot density in all grey levels, if

the vertex number equals the region’s number.

In the previous research, (Ostromoukhov and

Hersch,1999; Tu et al, 2000) first generate a pseudo

random distribution of central point with space

filling curve in a 1024x1024 square areas. Then,

mark in a 1024x1024 reference image with a disk of

radius r when a central point is added. After all

pixels of the referenced image have been marked,

the central point set is ready for the next step. When

the disk covers pixels are beyond (0..1023, 0..1023),

the pixels of coordinate mod by 1024 will also be

marked. The mod operation makes the central point

image mosaic seamlessly. Because Delaunay

triangulations maximize the minimum angle of all

the angles of the triangles in the triangulation, they

tend to avoid skinny triangles. Delaunay

triangulation is a good choice of geometry

subdivision to produce a hybrid dithering matrix

with favourable clustered dot shape. However, the

clustered dot density in highlight is greatly different

from the clustered dot density in shadow area.

Figure 1 and Figure 2 altogether show this

difference. Figure 1 and Figure 2 are the enlarged

detail of highlight and shadow of Figure 5 in

(Ostromoukhov and Hersch,1999). There are 7

positive clustered dots inside the marked circle of

Figure 1, whereas there are 13 negative clustered

dots inside the same sized circle of Figure 2.

Because of the great differences of clustered dot

densities and minimum dot size constraint for offset

printing, a comparatively low clustered dot density

has to be selected.

To explain the observation of Figure 1 and

Figure 2 theoretically, the research in

(Xu and Tan, 2009) deducted two theorems from

Euler formula.

[Theorem 1] G is a Delaunay triangulation

pattern that could be seamlessly tiled. The total

number of vertex, edges and faces of G are V, E and

F. Ｆ= V/2+2.

Proof: Because G is a geometry subdivision that

can be tiled seamlessly, it can be converted to a

multi-face object without hole and Euler formula can

be applied to G.

V-E+F=2 (1)

Every triangle has three edges and every edge is

shared by two triangles, so 3F=2E.

E=(3/2)F

(2)

Replace E in (1) with left side of (2):

V-(3F/2)+F=2

V=F/2+2 (3)

The geometry subdivision adopted to construct

dithering matrix usually has more than 1,000 faces.

Divide the two sides of equation (3) by F, we have

V:F≈1:2. [Theorems 1] explains why the ratio of

clustered densities in light and shadow areas is about

0.5.

[Theorem 2] G is a geometry subdivision that

can be tiled seamlessly. The total vertex, edges and

faces of G are V, E and F. If all the faces of the

division are quadrilaterals, then F=V-2.

Proof: Same as proof above:

V-E+F=2 (4)

If all faces of the G are quadrilaterals, every

quadrilateral has 4 edges and every edge is shared by

two quadrilaterals. So, 4F=2E

E=2F

(5)

Replace E in equation (4) with 2F

V-2F+F=2

F=V-2

[Theorems 2] suggests: if the geometry

subdivision compromises more quadrilaterals, the

ratio of the clustered dot densities in shadow and

light areas is closer to 1. According to [Theorem 2],

CONSTRUCTING THE HYBRID DITHERING MATRIX WITH EQUAL CLUSTERED DOT DENSITY

an optimized algorithm is designed to merge

triangles of Delaunay triangulation as much as

possible while trying to keep quadrilaterals merged

in good shape. In the research of (Xu and Tan, 2009),

the ratio of the clustered dot densities was improved

to 0.9 from 0.5 without any change to the central

point set.

This research adopts an approach different from

the optimizing algorithm in (Xu and Tan, 2009). It

first expands pseudo random central point set. Then,

it makes an all-quadrilateral subdivision with the

expanded central point set. A dithering matrix of

equal clustered dot densities is constructed, based on

the all-quadrilateral geometry subdivision. Because

this approach changes the initial central point set, a

further study on the uniformity of the expanded

central point set is conducted by comparing its

PSNR with PSNR of the images of the central point

set generated with different pseudo seeds.

4 ALL-QUADRILATERAL

GEOMETRY SUBDIVISION

In the first step of this research, we generate an

initial central point distribution over halftone plane

by using the algorithm 1-3 of (Xu and Tan, 2009).

The radius r defines minimum distance between

central points. In the experiment, r is set to 14. In the

second step, we calculate the Voronoi graph with the

central point set. Delaunay triangulation is obtained

by connecting the neighbouring central points in the

two regions which share the same edge of the

Voronoi graph.

’

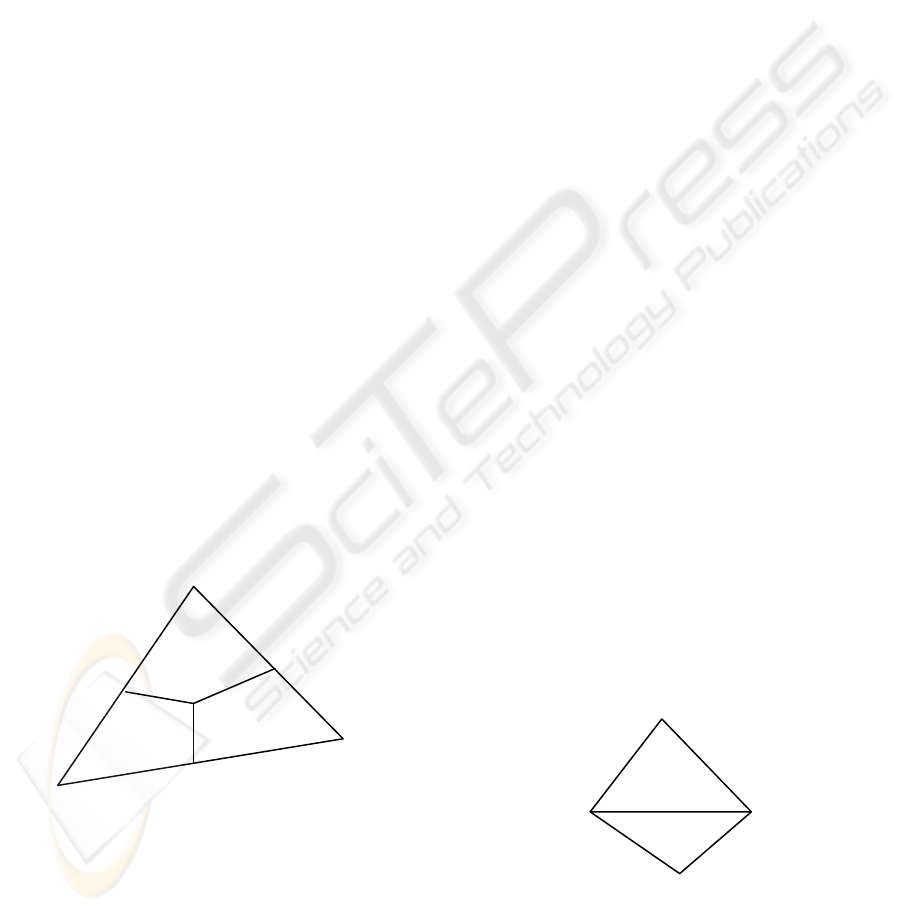
Figure 4: Split a triangle into quadrilaterals.

Now, take a triangle in Delaunay triangulation as

an example to explain the principle to construct all-

quadrilateral geometry subdivision. First, find the

weight of the triangle ABC in point P. Next, connect

P with three central points of the three edges of the

triangle ABC. The triangle is split into three

quadrilaterals (Figure 4). Then, all the triangles of

Delaunay triangulation will be converted to

quadrilaterals in this way. The new subdivision is

different from the optimized subdivision of (Xu and

Tan, 2009) in the following two aspects:

(1) The new geometry subdivision is

constructed with a central point set expanded from

the initial central point set by adding the weight

points and central points of edge of triangles.

(2) All regions of the new geometry

subdivision are quadrilaterals, whereas the regions

of the geometry subdivision optimized in (Xu and

Tan, 2009) are a combination of quadrilaterals and

triangles.

The vertex of the geometry subdivision is taken

as the centre of the negative clustered dot. The

image composed of the central points can also be

regarded as a halftone image of minimum non-zero

grey value. The image composed of the central

points can mosaic seamlessly according to the

previous description. We will further discuss the

quality issue of quadrilaterals.

The region’s narrow shape in the geometry

subdivision should be avoided, because the clustered

dot is formed in the region. By following the

definition of Delaunay triangulation, a quadruple is

defined as the quality factor the quadrilaterals (Xu

and Tan, 2009). When merging triangles besides an

edge into quadrilateral (Figure 5), quality factor of

(or edge A

) is calculated as follows:

Firstly, convert the angles of quadrilateral

to A

′, A

′ and A

′ according to

formula (6). Then, sort the angles in ascend order

and put it in a quadruple like (A

′, A

′)，

where i

∈{1,2,3,4}，A

′≤A

′.

The quadruple is called quality factor of

quadrilateral A

(6)

Figure 5: Defining quality factor of a quadrilateral.

For the convenience of comparing the quality of

quadrilaterals in geometry subdivision of this

research and (Xu and Tan, 2009), the quadruple is

{

′

>=180

, A

<=90

180-A

180>A

>90

IMAGAPP 2010 - International Conference on Imaging Theory and Applications

converted to a real value QF in conformity with

formula (7). The value QF ranges from 0 to 7.9.

QF=log

′

+ A

′

90+A

′)

(7)

The greater value of QF indicates better quality

of the quadrilateral. We calculate QF of

quadrilaterals in geometry subdivision of this

research and (Xu and Tan, 2009) and use Table 1 to

compare the quality of quadrilaterals in these two

subdivisions. In Table 1, Min_QF, Max_QF and

Average_QF are minimum, maximum and average

value of QF respectively. Table1 shows that quality

factor of the quadrilaterals in this research is better

than that in (Xu and Tan, 2009).

Table 1: Comparing QF of quadrilaterals.

Min_QF Max_QF Average_QF

All-

quadrilaterals

subdivision

7.6857 7.8218 7.7920

Optimized

subdivision in

(Xu and Tan,

2009)

7.4150 7.8218 7.7150

5 UNIFORMITY OF THE

EXPANDED CENTER POINT

SET

The purpose of this research is to produce a hybrid

dithering matrix with equal clustered dot densities.

Because some extra central points besides initial

central points are added in the process of obtaining

all-quadrilateral geometry subdivision, the expanded

central point set should be evaluated by comparing

its uniformity with that of the initial central point

set.

If the image of central points is regarded as a

1024x1024 halftone image, its average grey value g

is defined as:

(8)

NC is the number of central points and NP is the

total number of pixels of the image. The image of

central point can also be viewed as the result of

halftoning an image of constant grey value g. PSNR

(Peak Signal Noise Ratio) is often used to measure

the quality of image. In this research, the uniformity

of central point set is measured by PSNR defined in

the following procedure:

(1) Calculate the average grey value g;

(2) Filter the central point image with HVS

model and we get x(i,j), the human perceived image

of central point;

(3) Calculate PSNR with formula (9), where

max

is maximum grey value. Let it be 1.0 here.

PSNR=log(

max

((, ) )

ij g

−

∑∑

)

(9)

Greater PSNR means better uniformity for the

central point image. The expanded central point

image and initial central point image have different

dot densities. To reduce factors affecting the

comparing result, we scale down the expanded

central point image to the same dot density of the

initial central point image and crop it to 1024x1024.

The reason why we filter the image with HVS model

is that all printed halftone images are observed by

human eyes. It is due to the HVS model that the

halftone image looks similar to the original

continuous tone image. Table 2 lists PSNR of the

four central point images. D

is the expanded central

point image both cropped and scaled. D

is the initial

central point image. D

and D

are the central point

image that is generated with radius 14 and different

random seeds.

Table 2 shows PSNR of the tested pseudo

random central point images. PSNR of D

, D

and

varies in a range 43.3744~44.5205. PSNR of D

is out of this range. The quality (uniformity) of

expanded central point image D

is inferior to the

initial central point image D

. But PSNR of D

very close the above range. It is reasonable to think

PSNR of D

is still within the acceptable range.

Table 2: PSNR of image of central point set.

PSNR 43.1944 44.5205 43.3744 43.4002

g 0.0056 0.0051 0.0055 0.0055

6 CONSTRUCTING HYBRID

DITHERING MATRIX

In Section 4, the triangle of Delaunay triangulation

is split into three quadrilaterals to make an all-

quadrilateral geometry subdivision. Thus, we fill

these quadrilaterals with gradient tint to make a

dithering matrix.

CONSTRUCTING THE HYBRID DITHERING MATRIX WITH EQUAL CLUSTERED DOT DENSITY

Figure 6: Filling gradient in quadrilaterals.

Take the quadrilateral PC′AA′ as an example to

show the procedure of filling quadrilateral with

gradient tint (see Figure 6 also):

(1) Find the central point of all the four edges of

the quadrilateral PC′AA′ : K

, K

;

(2) Connect K

and K

with a line in between

. Connect K

and K

with a line in between

. O is the cross point of the line K

and K

Take O as the centre of positive clustered dot and

vertex P, C′, A, A′ as the centres of 4 negative

clustered dots;

(3) Fill quadrilateral OK

２

with gradient tint

a) Filling triangle K

２

the gradient tint

with 20 stages grey levels:

First, fill triangle K

with grey level

g=0.5；

Then, shift K

in the track of K

P and

P to K

′ and K

′ while keeping the line

′K

′ paralleled to K

; each step is 1/20 of

the distance from P to line K

; grey value g

filled is increased by 0.025 in each step;

b) Fill the gradient tint into triangle K

with 19 grey level stages;

First, fill grey level g=0.475 into triangle

；

Then, shift K

and K

in the track of K

and K

O to K

′ and K

′ while maintaining K

′

′ paralleled to K

; each step is 1/20 of the

distance from O to line K

, and grey value g

filled is decreased by 0.025 in each step;

(4) The same filling procedure will be applied to

quadrilaterals OK

C′K

, OK

and OK

A′K

The graphics of the dithering matrix image

described above is programmed in PostScript

language. With PostScript, it is easy to scale up and

down with ‘scale’ operator to produce the dithering

matrix of different clustered dot densities, which can

also be adapted to the output devices with different

resolutions.

The procedure to produce the dithering matrix is

described as follows:

First, we print the postscript file of dithering

matrix with Harlequin RIP and output it to a 600

DPI grey mode TIFF file. In Photoshop, the grey

image is smoothed by Gaussian filter to bring the

clustered dot a smooth edge. The parameters

employed in Gaussian filtering are: Radius=4,

Amount=100%. Next, we paste the above filtered

image into a new image of two different layers in

Photoshop. Then, we horizontally move the top layer

rightwards. When the left edge of the top layer

precisely matches the bottom layer, the distance by

which the top layer has been moved is the width of

pattern that can mosaic seamlessly. The size of the

image pattern that can mosaic seamlessly is a

2134x2134 image. Figure 7 is the mosaic unit

image. For clearness of the pattern, only a part of

image is shown in Figure 7. In the following step,

we directly convert the mosaic unit image to a

2134x2134 dithering matrix, in which the element

value of the matrix is the pixel value of the unit

mosaic image. Finally, we make a new dot shape

named ‘AccurateBalanced’ with the dithering matrix

and embed it into Harlequin RIP. Figure 8 and

Figure 9 are two samples produced with this dot

shape. From Figure 8 it is obvious that clustered dot

densities (98%) in shadow and light area (2%) are

the same. Figure 9 is an image halftone by the

Harlequin RIP with ‘AccurateBalanced’ dot shape.

Figure 7: Dithering

matrix.

Figure 8: Halftoned grey

image.

Figure 9: Halftoned image sample.

C’

’

B’

IMAGAPP 2010 - International Conference on Imaging Theory and Applications

7 CONCLUSIONS

This research proposes a new method to expand a

Delaunay triangulation to an all-quadrilateral

geometry subdivision. Based on the proposed

subdivision, we construct a hybrid dithering matrix

with equal clustered dot densities. The strengths of

this result are described as follows: (1) The clustered

dot density equals in all grey levels; (2) The quality

factor of the quadrilaterals is improved when

compared with that of the quadrilateral in the

optimized geometry subdivision in (Xu and Tan,

2009); (3) The uniformity of the expanded central

point set is proved to be acceptable by comparing its

uniformity with the variance of the uniformity of

central point distribution generated by different

pseudo random seeds.

The new hybrid dither matrix has an obvious

weakness: the shadow pattern consists of one big

negative clustered dot surrounded by several small

negative clustered dots (Figure 7). The big negative

clustered dot is centred on the vertex of the

geometry subdivision with five or more edges. The

small negative clustered dots are centred on the

vertex of 4 edges (central point of the edges of

Delaunay triangle) or on the vertex of 3 edges

(weight point of Delaunay triangle). The average

number of edges connected to a vertex is 4 for an

all-quadrilateral geometry subdivision. Further study

deserves to be conducted to make a geometry

subdivision with more 4 edges vertex to reduce the

local unbalance of the clustered dot size.

REFERENCES

Damera-Venkata N., Lin Q., 2003. AM-FM screen design

using donut filters.

Proc. SPIE,5293(469): 469–480.

Lau D. L., Arce G. R., Gallagher N. C., 1998. Green-noise

digital halftoning. Proc. IEEE,,86(12):2424–2444.

Lau D. L., Arce G. R., Gallagher N. C., 2000. Digital

color halftoning with generalized error-diffusion and

multichannel green-noise masks.

IEEE Trans. Image

Process.

, 9(5):923–935.

Ostromoukhov V., Hersch R. D., 1999. Stochastic

clustered-dot dithering. Journal of Electronic Imaging,

8(4): 439–445.

Tu Chang-He, Pan Rong-Jiang, Meng Xiang-Xu, 2000.

An algorithm for building stochastic clustered-dot

screens.

Chinese journal of computers,23(9):931-937

(in Chinese).

Ulichney R. A., 1988. Dithering with blue noise. Proc.

IEEE

, 76(1): 56-79.

Xu Guoliang, Tan Qingping, 2009. Research on balancing

clustered dot density for hybrid halftone dithering

algorithm.

Chinese journal of computers,.32 (8): 1550

1559 (in Chinese).

CONSTRUCTING THE HYBRID DITHERING MATRIX WITH EQUAL CLUSTERED DOT DENSITY