UTERINE FIBROID SEGMENTATION ON MRI BASED ON

CHAN-VESE LEVEL SET METHOD AND SHAPE PRIOR

MODEL

Alireza Fallahi, Mohammad Pooyan

Biomedical Engineering Department, Shahed University, Tehran, Iran

Hassan Hashemi

, Hassan Khotanlou

, Mohammad Ali Oghabian

, Kavous Firuznia

Advanced Diagnostic and Interventional Radiology Research, Tehran, Iran

Computer Engineering Department, Bu-Ali Sina University, Hamedan, Iran

Keywords: Uterine Fibroid, MRI Images, Image Segmentation, Chan-vese Level Set, Prior Shape Model.

Abstract: Uterine fibroid the most common benign tumor of the female pelvic affected 20%- 50% of the women in the

world. The efficacy of medical treatment is gauged by shrinkage of the size of these tumors after surgery.

Complex fibroids anatomy, nonhomogeneity region and missing boundary in some cases are a challenging

task in the segmentation. In this paper, we present a method to robustly segment these fibroids on MRI and

measure the volume. Our method is based on combination of two step Chan-Vese level set method and

geometric shape prior model. With calculating an initial region inside the fibroid using Chan-Vese level sets

method, rough segmentation obtained followed by a prior shape model. We found the algorithm efficient

and that it has some good results.

1 INTRODUCTION

Magnetic resonance image (MRI) is widely used in

radiology diagnosis especially in soft tissues.

Different modalities like T1, T2 and FLAIR and the

fusion of information provided by them can be

useful in diagnosis. One of the recent applications of

MRI is to diagnosis uterine fibroid. As the uterine

fibroid is the most common benign tumors of the

female pelvic (VeKaut, 1993), MR imaging can be

very useful in follow-up the patient condition,

diagnosis and treatment process (Cura and Bugnone,

2006). Uterine segmentation and volume

measurement is one of the important tasks that

usually is a time consuming and inaccurate work

when is performed manually. By automated and

semi-automated segmentation techniques we can

assist physicians to have a more accurate result and a

fast process. In (Guyon et al.,2003) geodesic active

contours and fast marching level set have been used

for segmenting fibroid and rigid landmark

registration has been applied for tracking its

variation over time. In (Jianhua et al, 2006) fast

marching level set has been used for initial

segmentation and Laplacian level set has been

applied to refine the segmentation result. These

methods can perform only in homogeneous and

connected boundary regions.

Even with great advantages of level set based

methods, active contours that are based on image

gradients are highly sensitive to the presence of

noise, poor image contrast and missing boundaries.

These lead to bad segmentation results. To

overcome these problems, some methods have

proposed robust region-based evolution criteria into

active contour energy function, built from intensity

statistics and homogeneity requirements (Paragios

and Deriche, 2002; Chan andVese, 2001). Prior

knowledge is usually very helpful to segment or

localize an anatomical structure. Several methods

have been proposed to incorporate prior shape

information into boundary determination. (Cootes et

al, 1995) have proposed an active shape model to

construct a statistical shape model from a set of

training images for image segmentation. The model

is built by outlining the contours and finding point

correspondences across shapes. (Staib and Duncan,

Fallahi A., Pooyan M., Hashemi H., Khotanlou H., Ali Oghabian M. and Firuznia K. (2010).

UTERINE FIBROID SEGMENTATION ON MRI BASED ON CHAN-VESE LEVEL SET METHOD AND SHAPE PRIOR MODEL.

In Proceedings of the International Conference on Imaging Theor y and Applications and International Conference on Information Visualization Theory

and Applications, pages 51-55

 SciTePress

1992) incorporate global shape information into the

segmentation process by using an elliptic Fourier

decomposition of the boundary and placing a

Gaussian prior on the Fourier coefficients.

(Leventon, 2000) incorporate statistical shape

influence into the evolution process of geodesic

active contours (Caselles, 1997) by attracting the

evolving contour toward the shape priors. The

correspondence problem is solved in their approach

by embedding the prior shape as the zero level set of

a level set function map. (Chen et al, 2001) propose

a variational method that minimizes an energy

function defined by the image gradients and the

shapes of interest. (Bresson et al., 2006) propose a

method by combination of region, boundary and

shape features based on Mumford-Shah function

(Mumford and Shah, 1989), level set approach and

prior shape model that is based on PCA of training

data to robustly segmentation.

In this paper we propose a tow step method for

robustly segmentation of uterine fibroids. First raw

segmentation obtained using Chan-Vese level set

method based on Mumford-Shah function. Then

segmentation is refined by applying prior shape

model using Bresson et al, method. In the proposed

method, the previous training data is not required.

We generate training data from ellipses model of the

segmented region.

In section 2 we describe the first step prior

segmentation using Chan-Vese level set method.

Section 3 explains the segmentation refinement

based on Bresson et al. prior shape model. Section 4

presents the segmentation results obtained by the

proposed approach. Section 5 presents some

conclusions and future extensions to this approach.

2 INITIAL SEGMENTATION

BASED ON CHAN-VESE LEVEL

SET METHOD

All classical snakes and active contour models are

based on edge-function depending on the image

gradient. These models can detect only objects with

edges defined by gradient to stop the curve

evolution. In practice, the discrete gradients are

bounded and then the stopping function is never zero

on the edges and algorithm fail to segment region.

(Chan and Vese, 2001) proposed a different

active contour method, that is not based on the

gradient of the image for the stopping process. The

stopping term is based on Mumford–Shah

segmentation techniques (Mumford and Shah,

1989).

The Mumford–Shah function for segmentation

is:











dxdyyxu

dxdyyxuyxu

CLengthcuF

),(|

|),(),(

)(.),(





(1)

Where

Ru :

is a given image,



and



are positive parameters. Their active contour model

is a particular case of the minimal partition problem,

in which they look for the best approximation

, as a function taking only two values, namely

and with one edge C, represented by the snake or the

active contour. This particular case of the minimal

partition problem can be formulated and solved

using the level set method (Osher and Sethian 1988).









outsideCuaverage

insideCuaverage

)(

(2)

Associated Euler–Lagrange equation deduced

for



represented in equation 3 which parameterize

the descent direction by an artificial time

0t

The

equation

),,( yxt



(with

),(),,0(

yxyx





)

defining the initial contour is:











),0(0])(

)()()[(

202

101

incu

cuvdiv









(3)

 inyxyx ),(),,0(









)(





In uterine fibroids that have a calcified and

infarcted region, edge based method fail to segment

whole region. We applied this method to the images

for initial segmentation. The segmentation is then

performed in whole image with initial manual region

in first slice. Figure.1 shows segmentation result in

some steps for a sample image.

IMAGAPP 2010 - International Conference on Imaging Theory and Applications

Figure 1: Result of applying Chan-Vese method, a: Initial

manual contour in the region, b and c: Evolving level set

to region boundary, d: Final segmentation result.

3 SEGMENTATION REFINMENT

USING ACTIVE PRIOR SHAPE

MODEL

The shape prior can be defined by different models

such as Fourier descriptors, medial axis or atlas-

based parametric models. Recently, the level set

representation of shapes has been employed as a

shape model (Leventon et al., 2000; Paragios et al.,

2003; Charpiat et al., 2003). This shape description

presents strong advantages since parameterization

free. It can represent shapes of any dimension such

as curves, surfaces and hyper-surfaces and basic

geometric properties such as the curvature. Finally,

this shape representation is also naturally consistent

with the level set framework of active contours. In

(Leventon et al, 2000), authors have used a level set

representation to model the shape prior. They have

defined a shape model of the object of interest by

computing principal components analysis (PCA) of

training shapes embedded in level set functions.

They have then integrated this shape model in an

evolution equation to globally drive the active

contour towards the prior shape. However, their

evolution equation is not expressed by a partial

differential equation (PDE) and there is no

variational formulation associated with his evolution

equation.

Recently Bresson et al, have proposed a

variational approach following the energy functional

model of (Chen et al. 2002) where integrate the

shape prior of (Leventon et al, 2002). They added a

region-based energy term based on the Mumford-

Shah function (Mumford and Shah, 1989) to

improve the robustness of segmentation model with

respect of noise, poor image contrast and initial

position of the contour.

They proposed the following energy functional

to address the problem of object segmentation using

a geometric shape prior with local and global image

information:

),,,(

)(),,(

outinTpcaregionr

boundarybTpcashapes

uuXXF

CFXXCFF









(4)

With

dqqCqChxF

xpcashape

)()))((,(









(5)

dqqCqCIgF

boundary

)()))(((







(6)









),(

)(

pca

Xout

pca

Xin

duuI

duuIF

ioutout

ininregion



(7)

where C is the active contour, φˆ is the shape

function of the object of interest given by the PCA

pca

is the vector of PCA eigen coefficients, h

is an

element of a group of geometric transformations

parameterized by x

(the vector of parameters), g is

an edge detecting function



and



out

are the

inside and outside regions of the zero level set of φˆ,

and u

out

are smooth approximations of the

original image I in



and



out

and β

, β

are

arbitrary positive constants that balance the

contributions of the boundary, shape and region

terms .We chose β

, β

, 1, 1/3 and 10

respectively.

3.1 Training Data for Computing PCA

The above method needs some initial training data

for calculating PCA eigen coefficients. Because of

explicit algebraic form we use ellipse model for

generating this training data based on region that

segmented from past stage. We calculate statistical

properties of the region: center, major axis, minor

axis and orientation. Then we generate ellipses

based on these parameters and some variations of

them for calculating PCA. Figure.2 shows generated

training data for segmented region.

We applied this method to refine segmented

region and consider active contour as a segmentation

result. Figure.3 shows the results.

UTERINE FIBROID SEGMENTATION ON MRI BASED ON CHAN-VESE LEVEL SET METHOD AND SHAPE

PRIOR MODEL

Figure 2: Training data generated from ellipse model of

segmented region.

Figure 3: Refined segmented region based on Bresson et

al, method and ellipses model; green contours denotes

shape model and red contours denote active contour.

4 RESULTS

We have used the above mentioned method on the

dataset containing the MR images of 5 patients that

were acquired at the Imam Khomeini hospital

Medical Imaging Centre. All the patients were

imaged on a 1.5T MR scanner used standard clinical

imaging protocol to obtain T2-weighted. Each MR

image has an in-plan resolution of 512×512 and slice

thickness of 5 mm with 15-20 slices.

Fig. 4 shows the segmentation results. With

manual initial region selection on first slice, other

slices were automatically segmented. The curves are

able to converge on the desired boundaries even

though some parts of the boundaries are too blurred

or missed to be detected by only gray level

information. To validate the segmentation results,

we compare obtained results with manual

segmentation performed by a senior radiologist. We

used four measures to evaluate the results which are

(M denotes the manually segmented area and an

automated segmented area):

• Similarity index:

%100*





Where

the number of true positive voxels and

is the cardinality of M and

is the

cardinality of A;

• Jaccard index:

%100*

TAM

NNN





• Hausdorff distance between A and M, defined

as HD = max (h (M, A), h (A, M)) where h (M, A) =

maxm∈M mina∈A d (m, a), and d (m, a) denotes the

Euclidean distance between m and a (m and a are

points of M and A, respectively).

•Average distance (MD) between the surfaces of

M and A.

As seen in Table 1 similarity index varies from

87.26% to 90.1% with a mean of 87.70%. The

Jaccard index varies from 74.65% to 82.62% with a

mean of 76.62% which shows a good accuracy of

segmentation. The average of Hausdorff distance is

3.42mm that smaller than a voxel size, and

constitutes good result. The mean value of the

average distance is 0.35mm that represented

accuracy of segmentation. Segmentation of fibroids

that have calcified and infarcted regions is a

challenging task due to global nonhomogenities.

Two published papers in uterine fibroid

segmentation used level set and active contour

methods. These methods are gradient based and are

not able to segment these types of tumors. Thus,

they only can be useful for complete infarcted

fibroids with clear boundaries. We have tried to

overcome these limitations by introducing a new

method that allows segmentation of these tumors by

region based method as initial segmentation. Then,

we applied combination of level set based and prior

shape model as final segmentation.

Table 1: Evaluation of the segmentation results of images

for which a manual segmentation was available.

Patient

Volume

metric (%)

Distance

metric(mm)

88.29

79.76

2.92

0.27

88.1

78.9

3.18

0.21

90.1

82.62

3.76

0.32

87.26

77.55

3.03

0.29

84.79

74.65

4.3

0.65

Average

87.70

78.62

3.42

0.35

IMAGAPP 2010 - International Conference on Imaging Theory and Applications

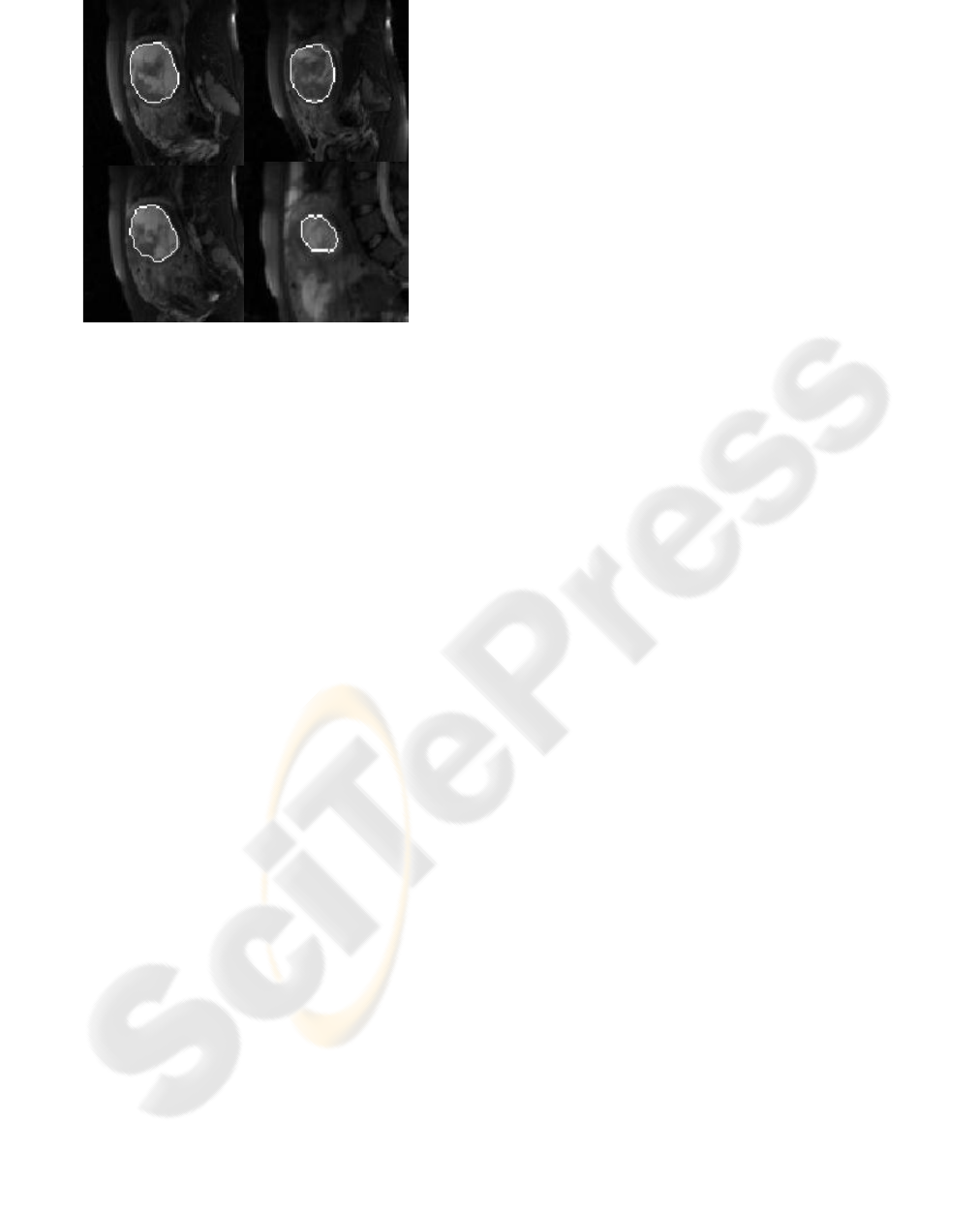
Figure 4: segmentation result using proposed method for

some slices of a patient.

5 CONCLUSIONS

This paper proposed an automatic method for the

segmentation of uterine fibroid in MR images. Using

Chan-Vese method initial segmentation obtained. In

second step segmentation refined by applying prior

shape model based on Bresson et al, method and

ellipses model. The quantitative results illustrate the

good performance of this method according to

nonhomogeneity region and missing boundary in

these types of fibroids. By uterine fibroid

segmentation in the future works we can analyze

fibroid properties like infarcted or calcified percent

region. This task has essential features in diagnosis

and treatment of uterine fibroids.

ACKNOWLEDGEMENTS

The authors would like to thank Dr A.Jalali and Dr

M.Shakiba of the Diagnostic and Interventional

Radiology Research Center (ADIR) for supplying all

patient images.

REFERENCES

Bresson, X., Vandercheynst, P., and Thiran, J.P., 2006, A

Variational Model for Object Segmentation Using

Boundary Information and Shape Prior Driven by the

Mumford-Shah Functional. International Journal of

Computer Vision, 68(2):145-162.

Caselles, V., Kimmel, R., and Sapiro, G., 1997, Geodesic

active contours, Int. J. Computer Vision, 22(1); 61–

79.

Chan, T.F. and Vese, L.A. 2001. Active contours without

edges. IEEE Transactions on Image Processing,

10(2):266–277.

Charpiat, G., Faugeras, O., and Keriven, R. 2003. Shape

metrics, warping and statistics. In IEEE International

Conference on Image Processing, 627–630.

Chen, S. Thiruvenkadam, H. D. Tagare, F. Huang, D.

Wilson, and E. A. Geiser, 2001, On the incorporation

of shape priors into geometric active contours, IEEE

Workshop on Variational and Level Set Methods in

Computer Vision, 145–152.

Cootes, T, F,. Taylor, C, J,. Cooper, D, H and Graham, J,

1995, Active shape models – their training and

application, Computer Vision Image Understand., 61

(1);38–59.

Cura M, Cura A , Bugnone A,. 2006, Role of Magnetic

Resonance Imaging in Patient Selection for Uterine

Artery Embolization. Acta Radiol ; 1105-1114.

Guyon J.P, Foskey M,Kim J, Firat Z, Davis Ylward B,.

2003, VETOT,Volume Estimation and Tracking Over

Time:Framework and Validation. Proceedings in

MICCAI; 142:149.

Jianhua Y , Chen D, Wenzhu L , Premkumar A., 2006,

Uterine fibroid segmentation and volume

measurement on MRI. Progress in biomedical optics

and imaging;(7)

Leventon, M. E,. Grimson, . W, E, L. and Faugeras,

2000, Statistical shape influence in geodesic active

contours, in Proc. IEEE Computer Society Conf.

Computer Vision and Pattern Recognition (CVPR),

;316–323.

Mumford, D. and Shah, J., 1989, Optimal approximations

of iecewise smooth functions and associated

variational problems. Communications on Pure and

Applied Mathematics, 42:577–685.

Osher, S. and Sethian, J.A. 1988. Fronts propagating with

curvaturedependent speed: Algorithms based on

Hamilton-Jacobi formulations. Journal of

Computational Physics, 79(1):2–49.

Paragios, N., Rousson, M., and Ramesh, V. 2003. Non-

rigid registr ation using distance functions . Journal of

Computer Vision and Image Understanding, 89(2–

3):142–165.

Staib,V and, Duncan, J,S, 1992, Boundary finding with

parametrically deformable models, IEEE Trans.

Pattern Anal. and Machine Intell., vol. 14, no. 11, pp.

1061–1075, 1992.

VeKaut, M, B,. 1993, Changing trends in treatment of

leiomyomata uteri. Curr Opin Obstet Gynecol 5:301.

UTERINE FIBROID SEGMENTATION ON MRI BASED ON CHAN-VESE LEVEL SET METHOD AND SHAPE

PRIOR MODEL