A SHAPE DESCRIPTOR BASED ON SCALE-INVARIANT
MULTISCALE FRACTAL DIMENSION
V´ıtor Baccetti Garcia and Ricardo da S. Torres
Institute of Computing, University of Campinas (Unicamp), Campinas, Brazil
Keywords:
Content-based image retrieval, Shape description, Image foresting transform, Multiscale fractal dimension.
Abstract:
This paper proposes a new scale-invariant shape descriptor based on the Multiscale Fractal Dimension (MFD).
The MFD is a curve that describes boundary complexity and self-affinity characteristics by obtaining fractal
dimension values as function of Euclidean morphologic dilation radii. Using this concept, which guarantees
rotation and translation invariance, we introduce a new scale-invariant descriptor that is obtained by selecting
a relevant fragment of this curve using a sliding window. The novel shape descriptor is compared with the
Multiscale Fractal Dimension and four other shape descriptors. Experimental results demonstrate that the new
descriptor is scale-invariant and yields very good results in terms of effectiveness performace when compared
with well-known shape descriptors.
1 INTRODUCTION
Image collections have been growing rapidly over the
last years (Datta et al., 2008), motivating the research
of new indexing and retrieval techniques. Content-
based image retrieval (CBIR) is a prominent topic
and proposes to index images based on their visual
properties. In order to achieve this objective, relevant
features (image signatures) must be extracted by low-
level descriptors and stored into databases. By defin-
ing a distance function to compare different signa-
tures, it is possible to retrieve images that form clus-
ters in the feature space and are assumed to be per-
ceptually similar.
Among the most used low-level features, one
can mention colour, texture, shape and spatial loca-
tion (Liu et al., 2007). Shape is considered an impor-
tant characteristic and is useful to accurately describe
and distinguish segmented objects. Typical properties
expected from shape descriptors include invariance to
translation, rotation, and scale. Moreover, shape de-
scriptors should be robust to noise, occlusions, and
distortions.
Many shape descriptors have been proposed in lit-
erature. They are usually classified into two cate-
gories: contour-based and region-based (Zhang and
Lu, 2004). As their names imply, the former uses only
boundary information whilst the latter employs all the
image pixels for obtaining a feature vector. Shape de-
scriptors can be further classified between global (in
which the contour or region is analysed as a whole)
and structural (where smaller primitives are studied
separately).
In this paper, a new shape descriptor is proposed,
a global contour-based descriptor that exploits fractal
theory concepts to describe boundaries. Fractal ge-
ometry (Mandelbrot, 1982) is a field of mathematics
that aims to analyze complex shapes. This theory has
been widely used in the image processing literature,
especially for texture segmentation (Chaudhuri and
Sarkar, 1995) and image compression (Fisher, 1995).
One of its fundamental definitions is the fractal di-
mension (FD), a measure of complexity that general-
izes the topological dimension concept.
The Multiscale Fractal Dimension (MFD) is an
extension of the Minkowski-Bouligand Fractal Di-
mension, using Euclidean morphological dilations for
multiscale representation. Basically, it encodes the
value of the fractal dimension as a function of the di-
lation radius (Costa et al., 2001). An efficient linear-
time algorithm for computing the MFD was proposed
in (da S. Torres et al., 2004). This method uses the
Image Foresting Transform (IFT) (Falc˜ao et al., 2004)
– a graph-based approach for the design of operators
employing connectivity characteristics.
In (da S. Torres et al., 2004), it is also described
how to use MFD as a shape descriptor. Basically,
MFD curves are used as feature vectors and are com-
pared using the Euclidean distance. Good results in
terms of effectiveness were reported in that article. In
185
Baccetti Garcia V. and da S. Torres R. (2010).
A SHAPE DESCRIPTOR BASED ON SCALE-INVARIANT MULTISCALE FRACTAL DIMENSION.
In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 185-190
DOI: 10.5220/0002831301850190
Copyright
c
 SciTePress

(a) (b)
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
1.3
1 2 3 4 5 6 7
Fractal dimension (F(r))
Dilation radius (r)
s
1
= 0.5
s
2
= 1.0
s
3
= 2.0
(c)
Figure 1: (a) An image extracted from the MPEG-7 data
set (Bober, 2001). (b) Dilated contours of (a). (c) The MFD
curves of rescaled versions of this image (each of them us-
ing a scale factor s
i
).
spite of these positive initial results, the MFD shape
descriptor has deficiencies regardingscale variance. It
can be observed that large contours tend to have frac-
tal curves shifted towards higher dilation radii (see
Figure 1). This phenomenon is expected, as smaller
contour details become indistinguishable for lower di-
lation radii, leading to an earlier fall of the curve and
a consequent “shift” between feature vectors. In or-
der to achieve scale invariance, it is important that the
curves are somehow “aligned”.
The descriptor proposed in this paper is based on
the Multiscale Fractal Dimension. It introduces a dif-
ferent feature extraction method that guarantees in-
variance to translation, rotation, and scale transfor-
mations. The main changes to the original MFD al-
gorithm are the use of a normalization step prior to
the execution of the IFT, a new MFD extraction strat-
egy that guarantees longer fractal dimension curves,
and the use of a sliding window for selecting relevant
information from the MFD curve. The same distance
function, the Euclidean distance, is applied.
Validation was conduced in two different data sets
in order to verify the general effectiveness as well as
its sensitivity towards the scale transformations. The
first database is composedof 99 images (9 classes) be-
ing subject to variations in form and also occlusion,
articulation, missing parts and segmentation-like er-
rors (Sebastian et al., 2004). The second set was de-
rived from the MPEG-7 database (Bober, 2001), with
700 images divided into 70 classes. Precision × Re-
call (Muller et al., 2001) is used to objectively analyze
obtained results.
The proposed descriptor is compared to four
other approaches available in literature: Beam an-
gle statistics (Arica and Vural, 2003), Fourier De-
scriptors (Gonzalez et al., 2004), Moment Invari-
ants (Hu, 1962), and Segment Saliences (da S. Torres
and Falc˜ao, 2007). Results have shown that the novel
descriptor is scale-invariant being comparable to the
best descriptors used as baselines in the Kimia data
set (Sebastian et al., 2004).
This paper is organized as follows: section 2
presents related work; section 3 describes the pro-
posed scale-invariant shape descriptor; section 4 de-
scribes conductedexperiments and discusses obtained
results; finally, section 5 states the conclusions and
discusses future work.
2 RELATED WORK
This section presents the Image Foresting Transform
(IFT) (Falc˜ao et al., 2004) and describes its use for
obtaining the MFD (da S. Torres et al., 2004).
2.1 Image Foresting Transform
The Image Foresting Transform (IFT) (Falc˜ao et al.,
2004) is a discrete approach for the design of im-
age processing operators based on connectivity prop-
erties. The main idea of this method is to reduce
the common image partition problem to find the
minimum-cost path forest in a graph.
In this paper, we use the Euclidean Distance
Transform (EDT) implemented with the IFT (Falc˜ao
et al., 2004; da S. Torres and Falc˜ao, 2007). The ad-
vantage of computing the EDT via IFT is that its time-
complexity is linear.
2.2 Multiscale Fractal Dimension
This section describes an efficient algorithm
(da S. Torres et al., 2004) for computing Multiscale
Fractal Dimension using the Euclidean Distance
Transform obtained with the Image Foresting
Transform (IFT).
There are several definitions for fractal dimension
(Mandelbrot, 1982). Among these definitions, the
Minkowski-Bouligand Fractal Dimension has been
one of the most popular in the image analysis com-
munity. It can be evaluated by a few different algo-
rithms (Costa et al., 2001). This fractal dimension
is defined as: F = 2 − lim
r→0
logA(r)
log(r)
, where A(r) is
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
186

the area of a region dilated by a radius r (see Fig-
ure 1(b)). The three-step algorithm, described next,
is used to compute the Minkowski-Bouligand fractal
dimension:
1 - Obtaining the Euclidean Distance Transform.
This part consists in the execution of the Image
Foresting Transform for obtaining the EDT of the
contour. As it will be discussed further ahead, the
maximum dilation radius for which the EDT is com-
puted is an important factor for obtaining scale-
invariance. For implementation purposes, the max-
imum dilation radius depends on the size of a large
empty frame placed around the input image.
2 - Evaluating Areas of Dilated Contours. By eval-
uating the cumulative histogram of the cost map (the
EDT image), one can determine dilated regions’ ar-
eas. It is also necessary to compute the log×log of
this cumulative histogram.
3 - Regression and Estimation of the Multiscale
Fractal Dimension. A common approach for eval-
uating a single-valued fractal dimension is to lin-
early fit the logA(r) × logr curve and to consider
the fractal dimension F as 2 minus the angular co-
efficient. Analysing the definition of Minkowski-
Bouligand Fractal Dimension, a great similarity with
the differentiation can be found. Indeed, both con-
cepts are related to behaviour in an infinitesimal in-
terval. One intuitive generalization is to fit the curve
with a function f that is not necessarily a line (in
our implementation a polynomial f
n
(r) with degree
n greater than one). Therefore, instead of a single
scalar value, the dilated contours’ fractal dimensions
can be obtained as a function of their dilation radii:
F(r) = 2− f
′
n
(r).
In comparison to other methods for evaluation
the fractal dimension, this approach avoids the prob-
lem of finding a suitable interval for linear regression
(as non-linear behaviour is observed for high dilation
radii). Comparing to previous methods for extracting
the Multiscale Fractal Dimension (Costa et al., 2001),
the IFT-based approach does not suffer from undesir-
able oscillations caused by noise in the estimation of
the derivative of a sampled curve.
In Figure 2, there is an example of steps 2 and 3
using the contour shown in Figure 1(a). Figure 2(a)
shows the log×log cumulative histogram of the cost
map fitted with a polynomial of degree n (n = 25).
Finally, Figure 2(b) presents the multiscale fractal di-
mension. The feature vector contains 25 samples of
the MFD curve for r ∈ [1, 6].
8
9
10
11
12
13
14
15
0 1 2 3 4 5 6 7
log A(r)
log r
Experimental data
Fitted function
(a)
0.7
0.8
0.9
1
1.1
1.2
1.3
1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6
F(r)
r
MFD curve
(b)
Figure 2: Using the image shown in Figure 1(a), (a) its
log(A)(r) ×log(r) values fitted by a function f
n
and (b) its
Multiscale Fractal Dimension.
3 SCALE-INVARIANT
MULTISCALE FRACTAL
DIMENSION
The Scale-Invariant Multiscale Fractal Dimension
(SIMFD) aims to use the shape description proper-
ties of MFD curves while avoiding their sensitivity
towards scale change. As explained in the introduc-
tion (see Figure 1), larger images have shifted fractal
curves.
The proposed method used to avoid scale varia-
tion is based on the idea of aligning curves during the
feature vector evaluation. The alignment method re-
lies on extracting a fragment of the MFD curve using
a sliding window of fixed length. In order to guar-
antee that this window can extract relevant fragments
(those that characterize the complexity of a contour),
two strategies are used before the alignment: normal-
ization of the input image before computing the IFT,
and the use of a modified MFD extraction method.
These two strategies are explained, respectively, in
sections 3.1 and 3.2. The use of the sliding window
for selecting the relevant fragment of the MFD curve
is described in Section 3.3.
A SHAPE DESCRIPTOR BASED ON SCALE-INVARIANT MULTISCALE FRACTAL DIMENSION
187

3.1 Pre-IFT Scale Normalization
Fractal curves of very small images decrease very
quickly, not having enough information to charac-
terize the shape complexity. Such problem can be
avoided easily by defining a minimum size for the
area of the Minimum Bounding-Box (MBB) around
the object whose contour is being described. Images
that are below this threshold are rescaled. The thresh-
old value (minimum area) used in our experiments
was 512 × 512. Higher values did not improve the
effectiveness of the method significantly.
3.2 Maximum Dilation Radius for MFD
Problems can also happen when images are too large.
The difficulty is that fractal curves might fall too late,
hampering the definition of the suitable curve frag-
ment that should be used for shape description. In
order to solve this problem, we propose a modified
MFD extraction method.
In the technique described in Section 2.2, the
MFD curve is sampled in a fixed dilation radius in-
terval. The lower bound cannot be changed, as it is
directly impacted by the regression stability. The up-
per bound – the maximum dilation radius – can nev-
ertheless be modified. Our proposal is that this value
should be proportional to the square root of the image
area. In this way, fractal curves of large images are
longer, having enough information about the shape
complexity. In our experiments the upper bound value
t
ub
is defined as follow: t
ub
= 2×
√
A, where A is the
area of the object’s MBB.
3.3 Curve Fragment Selection
The following properties are true for a MFD curve
F(r) of a closed contour:







F(r) ∈ [0, 2]
max(F(r)) ≥ 1
lim
r→∞
F(r) = 0
(1)
(2)
(3)
where r is the dilation radius.
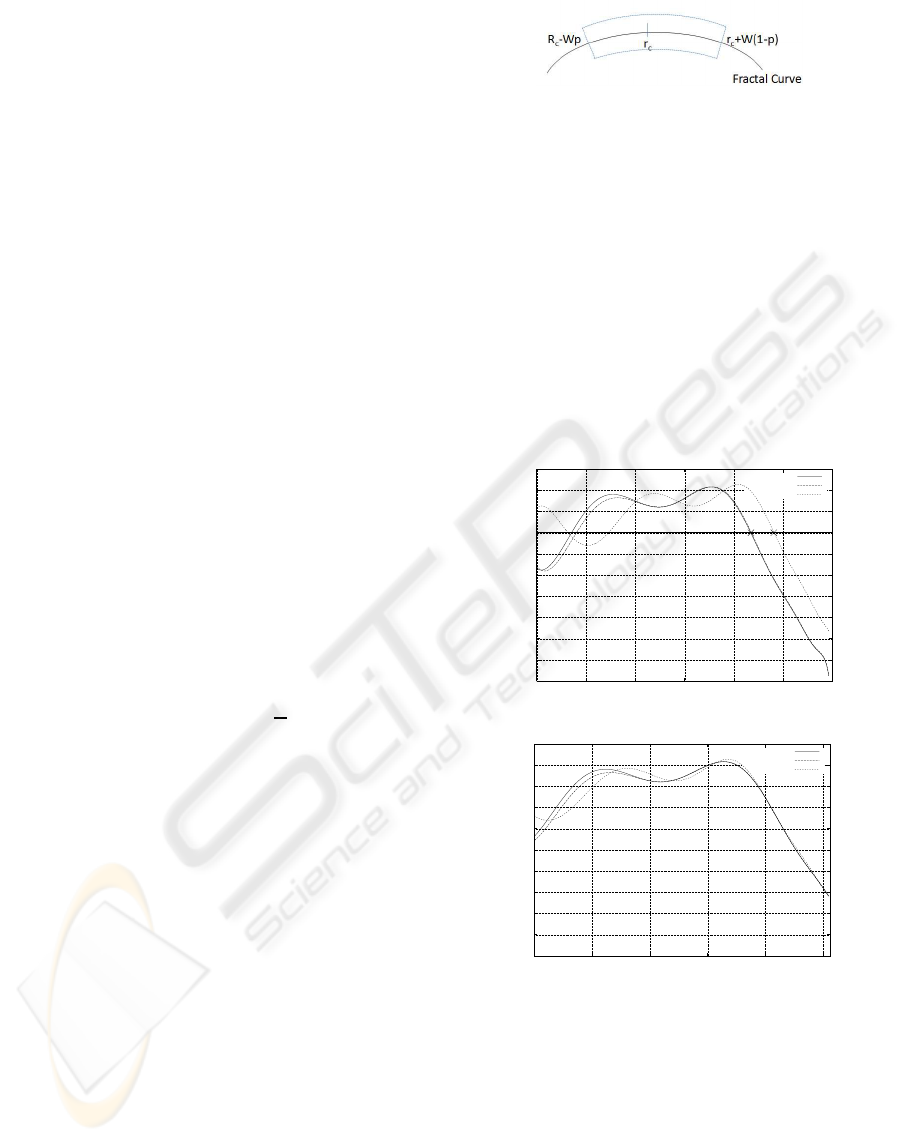
A sliding window of length W is used to find a ra-
dius r
c
in which F(r
c
) = F
c
for a fixed F
c
. The feature
vector is defined as the N multiscale fractal dimen-
sion values sampled in the interval [r
c
−W × p, r
c
+
W ×(1 − p)]. The parameter p is used to define the
proportion of points inside the window in which dila-
tion radii are smaller than r
c
. Figure 3 illustrates how
those parameters relate to each other.
Notice that, from Equations 2 and 3, if F
c
∈ [1, 0[
then there exists a r
c
in which F(r
c
) = F
c
. Therefore,
Figure 3: Window parameters.
if the curve is long enough, the radius r
c
can be found
by the sliding window. Moreover, it is necessary that
the sampling lower bound (r
c
−W × p) be larger than
the minimum dilation radius and that upper bound
(r
c
+W ×(1− p)) be smaller than the maximum dila-
tion radius. Those requirements are fulfilled by using
the approaches described in sections 3.1 and 3.2.
In our experiments, W = 5, p = 0.8, and F
c
= 1.0.
There are 256 samples and the polynomial degree is
25. Examples of feature vectors are shown in Fig-
ure 4. It is possible to see the normalization effects by
comparing these feature vectors to the MFD values in
Figure 1.
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
1.3
1 2 3 4 5 6 7
Fractal Dimension (F(r))
Dilation radius (r)
F
c
r
c
1
,
r
c
2
r
c
3
s
1
= 0.5
s
2
= 1.0
s
3
= 2.0
(a)
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
1.3
0 50 100 150 200 250
Fractal value
Feature vector bin
s
1
= 0.5
s
2
= 1.0
s
3
= 2.0
(b)
Figure 4: Results of the SIMFD for three rescaled versions
of Figure 1(a) using different scale factors’ values of s
i
: (a)
MFD curves prior to fragment selection (notice the x
ci
and
F
c
), (b) SIMFD feature vectors.
4 EXPERIMENTS
In this section, the proposed descriptor (SIMFD)
is compared with the earlier definition of MFD
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
188

(da S. Torres et al., 2004) and other shape descrip-
tors as well. Precision × Recall curves are used as
the effectiveness measure to evaluate performance.
4.1 Shape Data Sets
Finding good databases for shape description can be
difficult, as most of available data sets are formed
by colour and texture images. Moreover, contour-
based shape descriptors restrict even more the choice
of data sets, as images must have a single closed con-
tour without internal cavities. The MPEG-7 database
is extensively used in literature (Bober, 2001), how-
ever it has classes that might not be suitable to many
contour-based descriptors (see Figure 5). In our ex-
periments, the following data sets are employed:
Scale invariance tests data set: derived from the
Core Experiments Shape 1 Part B data set (Bober,
2001), this database contains 700 images divided into
70 classes. It has been created by randomly choosing
one image from each class of the former database and
by scaling them up and down by fixed factors.
Kimia-99 data set: this database has 99 im-
ages separated into 9 classes which have been sub-
ject to form variations as well as occlusion, articula-
tion, missing parts, etc. (Sebastian et al., 2004). This
database has been frequently employed for the vali-
dation of contour-based shape descriptors (Ling and
Jacobs, 2007; Yang et al., 2008).
Figure 5: Example of images of a MPEG-7 class that are
not suitable for contour-based shape descriptors.
Figure 6: Images of the Kimia-99 data set.
4.2 Descriptors used for Comparison
The new descriptor and the original proposi-
tion (da S. Torres et al., 2004) is referred as, respec-
tively, SIMFD and MFD. Besides these two algo-
rithms, the following descriptors are also used: Beam
0
0.2
0.4
0.6
0.8
1
0 0.2 0.4 0.6 0.8 1
Precision
Recall
Precision x Recall
BAS
FD
MFD
MI
SIMFD
SS
(a)
0
0.2
0.4
0.6
0.8
1
0 0.2 0.4 0.6 0.8 1
Precision
Recall
Precision x Recall
BAS
FD
MFD
MI
SIMFD
SS
(b)
Figure 7: Precision × Recall graphs for (a) the Scale invari-
ance data set, and for (a) the Kimia-99 shape data set.
angle statistics (BAS) (Arica and Vural, 2003);
Fourier Descriptors (FD) (Gonzalez et al., 2004);
Moment invariants (MI) (Hu, 1962); and Segment
saliences (SS) (da S. Torres and Falc˜ao, 2007).
4.3 Experimental Results
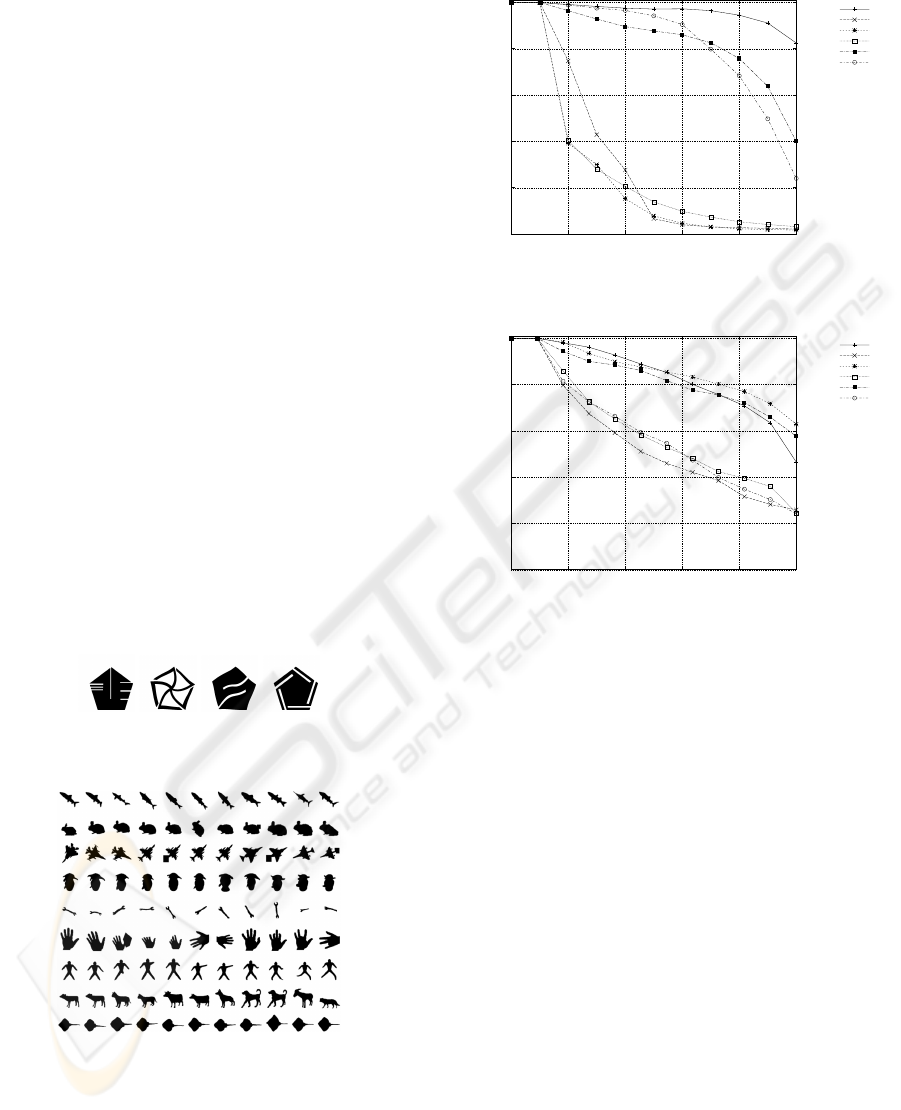
Considering the two data sets, the Precision × Recall
curves are shown in Figure 7. Regarding the scale in-
variance tests (Figure 7(a)), it can be observed that the
Scale-Invariant Multiscale Fractal Dimension is more
effective than the original MFD descriptor. Other de-
scriptors have different sensitivities to scale. BAS is
the most invariant descriptor.
For the general effectiveness experiments in the
Kimia-99 data set (Figure 7(b)), two different groups
of descriptors can be noticed in the Precision × Recall
graph. The effectiveness results of descriptors of each
group are almost the same. BAS, MFD, and SIMFD
yield the best effectiveness measures. FD, MI, and SS
have similar effectiveness performance, being largely
outperformed by BAS, MFD, and SIMFD, which
A SHAPE DESCRIPTOR BASED ON SCALE-INVARIANT MULTISCALE FRACTAL DIMENSION
189

have similar effectiveness performance. It is impor-
tant to note that in this data set there is almost no scale
variance (see Figure 6).
5 CONCLUSIONS
This article presented a novel shape description algo-
rithm, the Scale-Invariant Multiscale Fractal Dimen-
sion (SIMFD). This descriptor is based on the use
of the Fractal Dimension concept – a real number
that describes boundary complexity and self-affinity
characteristics. The proposed method relies on three
steps: a pre-IFT area normalization, the use of a new
algorithm for obtaining the multiscale fractal dimen-
sion, and the use of a method for extracting the most
relevant fragment of the MFD curve.
An experimental validation was conduced, com-
paring SIMFD to the Multiscale Fractal Dimension
and to four other shape descriptors. Experiments re-
sults have shown that the new descriptor is at least as
effective as the Beam Angle Statistics and the Mul-
tiscale Fractal Dimension, outperforming other well-
known shape descriptors. Moreover, it has been em-
pirically demonstrated that SIMFD is scale-invariant.
Future work includes extending the proposed de-
scriptor to more complex binary images (several con-
tours, cavities inside the shape, etc.). Extending the
description algorithm to grey-scale images is also be-
ing studied.
ACKNOWLEDGEMENTS
Authors thanks CNPq, CAPES, and FAPESP for fi-
nancial support.
REFERENCES
Arica, N. and Vural, F. (2003). BAS: a perceptual shape
descriptor based on the beam angle statistics. Pattern
Recognition Letters, 24(9–10):31–41.
Bober, M. (2001). MPEG–7 visual shape descriptors. IEEE
Transactions on Circuits and Systems for Video Tech-
nology, 11(6):716–719.
Chaudhuri, B. and Sarkar, N. (1995). Texture segmentation
using fractal dimension. PAMI, 17(1):72–77.
Costa, L., Campos, A., and Manoel, E. (2001). An inte-
grated approach to shape analysis: Results and per-
spectives. In International Conference on Quality
Control by Artificial Vision, pages 23–34.
da S. Torres, R. and Falc˜ao, A. (2007). Contour salience
descriptors for effective image retrieval and analysis.
Image and Vision Computing, 25(1). 3–13.
da S. Torres, R., Falc˜ao, A., and da F. Costa, L. (2004). A
graph–based approach for multiscale shape analysis.
Pattern Recognition, 37(6):1163–1174.
Datta, R., Joshi, D., Li, J., and Wang, J. Z. (2008). Image
retrieval: Ideas, influences, and trends of the new age.
ACM Computing Surveys, 40(2):1–60.
Falc˜ao, A., Stolfi, J., and de A. Lotufo, R. (2004). The
image foresting transform: Theory, algorithms, and
applications. PAMI, 26(1):19–29.
Fisher, Y. (1995). Fractal image compression: theory and
applications. Springer-Verlag, New York.
Gonzalez, R., Woods, R., and Eddins, S. (2004). Digital im-
age processing using MATLAB. Prentice Hall Upper
Saddle River, NJ.
Hu, M. (1962). Visual pattern recognition by moment in-
variants. IRE Trans. on Inf. Theory, 8(2):179–187.
Ling, H. and Jacobs, D. (2007). Shape classification using
the inner-distance. PAMI, 29(2):286–299.
Liu, Y., Zhang, D., Lu, G., and Ma, W. (2007). A survey of
content-based image retrieval with high-level seman-
tics. Pattern Recognition, 40(1):262–282.
Mandelbrot, B. (1982). The Fractal Geometry of Nature.
W. H. Freeman, San Francisco, CA, USA.
Muller, H., Muller, W., Squire, D., Maillet, S., and Pun, T.
(2001). Performance evaluation in content-based im-
age retrieval: Overview and proposals. Pattern Recog-
nition Letters, 22(5):593–601.
Sebastian, T. B., Klein, P. N., and Kimia, B. B. (2004).
Recognition of shapes by editing their shock graphs.
PAMI, 26(5):550–571.
Yang, X., Bai, X., Latecki, L. J., and Tu, Z. (2008). Improv-
ing shape retrieval by learning graph transduction. In
ECCV, pages 788–801.
Zhang, D. and Lu, G. (2004). Review of shape representa-
tion and description. Pattern Recognition, 37(1):1–19.
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
190