COMPLEMENTARITY OF FEATURE POINT DETECTORS

Guillaume Gales, Alain Crouzil

Institut de Recherche en Informatique de Toulouse, Univerist

e P. Sabatier

118 rte de Narbonne, 31062 Toulouse cedex 9, France

Sylvie Chambon

Laboratoire Central des Ponts et Chauss

ees, rte de Pornic, BP 4129, 44314 Bouguenais cedex, France

Keywords:

Feature points, Complementarity, Repeatability, Spatial distribution.

Abstract:

The goal of this paper is to provide a study on complementarity of feature point detectors. Many studies

have been proposed on these detectors but none deals with complementarity in details. We introduce an

evaluation of eleven well-known detectors based on new criteria used to characterize complementarity. The

complementarity is computed with spatial distribution and contribution measures as well as repeatability and

distribution gains of the association of two detectors.

1 INTRODUCTION

Many applications in computer vision rely on some

characteristic points called feature points (or point of

interest). Their detectors are designed to select the

most distinctive points in an image so they are easy to

match without ambiguities. We asked ourselves the

following question: if different feature point detectors

select the most distinctive points in an image, do they

return the same points ? In other words, we propose

to study the complementary of several feature point

detectors. Previous evaluations studied detection cri-

teria such as repeatability or information content and

matching criteria such as recall and precision rates.

We propose to study the complementarity of feature

point detectors based on new criteria: spatial distri-

bution and complementarity measures. The idea is to

ﬁnd out which are the most complementary detectors

in order to combine them when needed. Initially, this

evaluation is proposed on small-baseline stereo image

pairs since feature points may be used for instance

in application such as stereo matching (Lhuillier and

Quan, 2002) or fundamental matrix estimation (Hart-

ley and Zisserman, 2004).

First, previous work on feature point detectors is

described. Second, the new criteria to measure com-

plementarity are introduced. Finally, the results of our

experimentations are discussed before the conclusion.

2 PREVIOUS WORK

2.1 Feature Point Detection

Feature points are distinctive points within an image.

Therefore, they are used in many applications such

as tracking, indexation or stereo matching. There are

different families of detectors: contour based, inten-

sity based, parametric model based methods (Schmid

et al., 2000). We focus on intensity based methods

since they are widely used. They are based on the fol-

lowing steps: (i) computation for each pixel of a re-

sponse value based on local grey level variations ; (ii)

non maxima suppression ; (iii) post processing (edge

response elimination, subset selection, subpixel local-

isation). In this section we describe brieﬂy the ﬁrst

step for the well known detectors: Moravec, Harris,

Kitchen-Rosenfeld, Beaudet, SUSAN, FAST, SIFT,

SURF, Harris-Laplace, Hessian-Laplace and Kadir.

 Fixed Scale Detectors. The response is com-

puted using a ﬁxed window size.

Moravec (MO). The response is based on an

auto-correlation measure based on four direc-

tions (Moravec, 1977).

Harris (HA). The response is based on a generali-

sation of the auto-correlation measure on every shift

334

Gales G., Crouzil A. and Chambon S. (2010).

COMPLEMENTARITY OF FEATURE POINT DETECTORS.

In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 334-339

DOI: 10.5220/0002831703340339

 SciTePress

directions. It deﬁnes an auto correlation matrix, then

the response is obtained from this matrix. Several

variants were given (Harris and Stephens, 1988; No-

ble, 1988; Shi and Tomasi, 1994).

Kitchen-Rosenfeld (KR). The response is based on

the curvature of the grey level gradients (Kitchen and

Rosenfeld, 1982).

Beaudet (BE). The response is based on the de-

terminant of the Hessian matrix (second deriva-

tives) (Beaudet, 1978).

SUSAN (SU). The response is based on the area in

the neighbourhood of the same intensity as the current

pixel (Smith and Brady, 1997).

FAST (FA). The response is based on the conﬁg-

uration of the grey levels on a circle centred on the

current pixel (Rosten and Drummond, 2006).

 Multi Scale Detectors. The response is com-

puted using different window sizes (or image resolu-

tions).

SIFT (SI). The response is based on the grey level

Laplacian computed using a difference of Gaus-

sian (Lowe, 1999).

Harris-Laplace, Hessian-Laplace (HAL, HEL).

The response is based on Harris or the Hessian matrix

but the detected feature points must also be maxima

in the scale space of the Laplacian (Mikolajczyk and

Schmid, 2004).

SURF (SR). The response is based on the deter-

minant of the Hessian matrix. The detected feature

points must also be maxima in the scale space of the

determinant of the Hessian (Bay et al., 2006).

Kadir (KA). The response is based on the grey

level histogram entropy of the neighbours of the cur-

rent pixel (Kadir et al., 2004).

2.2 Previous Evaluations

Repeatability. When two images of a same scene

taken under different conditions are submitted to a

feature point detector, it is desirable that the returned

points are repeated: the two projections of a scene

point are detected in the two images. In other words, a

feature point in an image is repeated if its correspon-

dent in the other image is also detected as a feature

point. The repeatability rate of a detector is the per-

centage of repeated points from an image to another.

If this rate is high when a transformation between the

two images is large (rotation, scale change, perspec-

tive change, light change), this detector is robust to

that transformation (Schmid et al., 2000; Mikolajczyk

and Schmid, 2004; Gil et al., 2009).

Information Content. This value represents how

much the feature points of an image are distinct to

each other. The more distinctive the feature points

are, the less ambiguous they are to match. A descrip-

tor is computed for each feature point and the Ma-

hanalobis distance is used to normalize each compo-

nent (Schmid et al., 2000).

Complementarity. The complementarity is mea-

sured in (Mikolajczyk et al., 2005) in an object recog-

nition context. A clustering algorithm is applied to

the feature points, then the number of points from

each detector is computed for each class. Ideally, each

class must contain points from the same detector only.

3 PROPOSED EVALUATION

We propose to extend and modify the previous criteria

with the following ones:

• Spatial Distribution – distribution of feature

points is measured in depth discontinuity areas

and computed region wise ;

• Complementarity – complementarity of two de-

tectors is measured in three ways: contribution

measure ; repeatability gain and distribution gain.

The repeatability is taken into account by the com-

plementarity measures, therefore, we propose to com-

pute it using the deﬁnition below.

3.1 Repeatability

Let p

i, j

be the pixel at the i

row and j

column in

the image I. Let d

i, j

be the disparity vector such as

, j

= p

i, j

+ d

i, j

where p

, j

is the pixel in the right

image which is the projection of the same scene entity

as p

i, j

. Let ε be a tolerance margin in pixels. We use

the following deﬁnitions:

• repeated point – a feature point p

i, j

in the im-

age I

is repeated if a feature point p

, j

has

been detected in the image I

within a distance

lower than ε from its theoretical correspondent,

i.e. ||(p

i, j

+ d

i, j

) − p

, j

|| < ε.

COMPLEMENTARITY OF FEATURE POINT DETECTORS

335

• repeatability rate – the repeatability rate for a de-

tector D and an image pair (I

, I

) is given by:

rep(I

, I

) =

rep

→ I

) + rep

→ I

)

(1)

with

rep

(A → B) =

# feature pts. of A repeated in B

# feature points in A

(2)

3.2 Spatial Distribution

Distribution in Depth Discontinuity Areas. Depth

discontinuity areas are located near the boundaries be-

tween homogeneous depth regions. They result in

grey level variations. However, the grey level of the

background may be locally different for two corre-

spondents which makes such pixels harder to match

than pixels in other areas. Feature point detectors tend

to select points in areas where high grey level varia-

tions occur and therefore may return points in depth

discontinuity areas. Thus, we compute the following

measure:

DA =

# feature points in depth discontinuity areas

# feature points

(3)

Region Wise Distribution. The regions are ex-

tracted using a color segmentation algorithm. The

idea is based on the hypothesis that pixels with more

or less the same color belong to the same object part

(and therefore have more or less the same disparity

value). For a detector D, the region wise distribution

score is:

D,S

# regions holding at least one feature point

# regions

(4)

where S is a segmentation map. A low ratio reveals

a lack of feature points or a bad distribution over the

different regions of the image.

3.3 Complementarity

Contribution Measure. Let P

be the set of the

feature points returned by a detector D

and P

the

set of the feature point returned by a detector D

. The

contribution of D

over D

is given by:

contribution

card

{

}

− card

{

∩ P

}

card

{

}

(5)

where the intersection P

∩ P

is computed consid-

ering two points p

i, j

and p

, j

of an image I as the

50 100 150 200 250 300 350 400 450

100

150

200

250

300

350

50 100 150 200 250 300 350 400 450

100

150

200

250

300

350

− (P

∩ P

)

Figure 1: This ﬁgure shows on the left all the feature points

returned by HA and on the right the contribution of BE, i.e.

the feature points returned by BE which are different from

the ones already returned by HA (ε = 3). It also shows the

segmentation map (each color represents one region).

same point when ||p

i, j

− p

, j

|| < ε. The higher this

value is with a high ε, the larger the differences are

between the two sets P

and P

. This measure is

illustrated by ﬁgure 1.

This contribution measure is not symmetric since

the cardinalities of each detector are different, there-

fore in order to get an objective idea of the comple-

mentarity of the union of two detectors (D

, D

), we

compute:

contribution(D

, D

) = contribution(D

, D

)

= min(contribution

, contribution

)

(6)

Repeatability Gain. The repeatability is computed

independently for the detectors D

and D

. It is then

computed with D

which represents the union

∪ P

. The gain of repeatability is given by:

gain

rep

= rep

− max



rep

, rep



(7)

Distribution Gain. The spatial distribution is com-

puted independently for the detectors D

and D

. It

is then computed with D

which represents the

union P

∪ P

. The gain of distribution is given by:

gain

=RD

− max(RD

, RD

)

(8)

where S is a segmentation map.

4 DATA SET

4.1 Stereo Pairs

Stereo pairs from the Middlebury data set

are used

for this experimentation

. They present issues such as

vision.middlebury.edu/stereo/data/

We use the pairs named aloe, art, bowling1, cloth1,

cloth4, cones, dolls, midd2, moebius, plastic and teddy.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

336

occlusions and depth discontinuities. They are epipo-

lar rectiﬁed and the ground truth is known. However,

deformations between two images is not as important

as it could occur in applications such as indexation.

4.2 Implementation Details

The programs provided by the detector authors is used

when available: HAL

, HEL

, SU

, FA

, SI

, SR

and KA

. Our own implementation is used for the

other detectors. For each detector, the following pa-

rameters can have an inﬂuence on the result:

• Response Window Size (for ﬁxed scale detectors)

– the smaller this size is, the more the detector is

able to select small structures but the greater the

noise sensitivity is. On the other hand, the greater

this size is, the larger the smoothing effect is and

the greater localization errors are.

• Non Maxima Suppression Window Size – the

smaller this size is, the larger the number of de-

tected feature points is but these feature points

may be close to each other.

• Response Threshold – a threshold on the response

value is often used in order to get rid of false re-

sponses. The higher this value is, the smaller the

number of feature points is.

It would be interesting to study the inﬂuence of each

parameter on the result but this exhaustive evaluation

is difﬁcult to analyse. Moreover, for the detectors im-

plemented by their authors, we do not always have the

possibility to change all the settings. A normalization

would also be necessary on all the different values in

order to make them comparable. Facing this issue, we

decided to ﬁx these parameters once for all for each

detector. For the detectors we implemented, we used

parameter values that give good results with our ex-

perimentations. For the the other detectors, we used

the default values given by their authors.

5 RESULTS

5.1 Repeatability

The repeatability rep

of a detector D is given by

computing the mean value of the repeatability rates

robots.ox.ac.uk/˜vgg/research/afﬁne/

users.fmrib.ox.ac.uk/˜steve/susan/index.html

svr-www.eng.cam.ac.uk/˜er258/work/fast.html

cs.ubc.ca/spider/lowe/keypoints/siftDemoV4.zip

vision.ee.ethz.ch/˜surf/

robots.ox.ac.uk/˜timork/salscale.html

0 1 2 3

Repeatability (%)

HAL

HEL

Figure 2: Repeatability scores rep

for the tested detectors.

All the feature points are taken into account, therefore fea-

ture points in occluded areas decrease the score. The nota-

tions are deﬁned in § 2.1.

found over the data set. The repeatability is mea-

sured by taking ε ∈

{

0, 1.5, 3

}

. The results for re-

peatability are shown in ﬁgure 2. The detectors with

the best repeatability are HA, FA and SI. For ε = 0

the repeatabilities are very low. Therefore, a “fea-

ture points to feature points” matching strategy is not

advisable when high precision is required. We rec-

ommend a “feature points to neighbours of feature

points” matching strategy to settle this issue.

5.2 Spatial Distribution

The results for the depth discontinuity distribution are

shown in table 1. The depth discontinuity areas are

computed using the provided ground truth disparity

maps, see § 4.1. The results for the region wise dis-

tribution are shown in table 1. The EDISON

pro-

gram is used to compute two segmentation maps: (i)

an “under” segmentation S1 giving about 100 regions

for each image ; (ii) a “medium” segmentation S2 giv-

ing about 500 regions for each image (see ﬁgure 1).

The most signiﬁcant criteria, where the biggest

differences are obtained, are RD

D,S2

and Card. HAL

detector returns very few points and consequently

gives also the worst RD

D,S2

. On the other hand,

HA detector seems to obtain the best compromise

between cardinality, DA and RD

D,S2

. According to

these results, the best compromises is obtained by the

detectors HA, FA and SI.

5.3 Complementarity

Contribution Measure. This measure is computed

over all the feature points and over the repeated points

with ε = 3 (we consider this value as the minimum

caip.rutgers.edu/riul/research/code/EDISON/

COMPLEMENTARITY OF FEATURE POINT DETECTORS

337

Table 1: Mean cardinalities (Card.), mean of the distribu-

tion measures in depth discontinuity (DA), and mean of the

region based distribution measure (RD) with segmentation

S1 ans S2. For each column the best result is shown in bold.

D Card. DA% RD

D,S1

% RD

D,S2

BE 967 28 100 78

FA 2243 27 100 83

HAL 293 35 94 30

HA 989 25 99 86

HEL 1252 32 100 73

KA 638 29 99 61

KR 1153 31 100 81

MO 845 27 97 62

SI 1662 29 99 82

SR 303 31 99 49

SU 922 29 100 74

distance between two different points) in one hand

and ε = 12 (large enough value to see which detec-

tors return complementary feature points away from

each other) on the other hand. The results are shown

in table 2 (the measures are computed over all the fea-

tures points) and in table 3 (the measures are com-

puted over the repeated feature points). According to

these results, the most complementary detectors are

KA+SU, KA+MO and KR+HEL. By reading these

tables, we can see for instance that by taking the union

HA+SI, we add in the worst case 67% of new repeated

feature points within a distance of ε = 3 pixels of each

other and 2% of new repeated feature points within a

distance of ε = 12 (i.e. at least 12 pixels farther than

the already computed feature points).

Repeatability Gain. The results are shown in ta-

ble 4. They show which detectors are the most com-

plementary in terms of repeatability. First, it shows

the good complementarity of the following detectors

KR+HEL, HEL+SU and KR+SI. Second, it shows

which detector to use in combination to another in or-

der to improve the repeatability. The best repeatabil-

ity was given by FA, see § 5.1. Therefore, adding the

feature points from the detector HEL can improve by

2.12% the repeatability of FA.

Distribution Gain. The segmentation S2 is used

in our experimentation, see § 5.2. The results are

shown in table 5. They show which detectors are

the most complementary in terms of region based

distribution. First, it shows the good complementar-

ity of the following detectors KA+MO, KA+SU and

KA+SR. Second, it shows which detector to use in

combination to another in order to improve the spatial

distribution. The best region based distribution was

given by HA, see § 5.2. By reading table 5, we can

see that adding the feature points from the detector BE

can improve the distribution by 6.14% which gives a

Table 2: Contribution measures taking into account all the

feature points. For each couple of detectors D

, we

show contribution

. ε = 3 on the ﬁrst row and ε = 12

on the second row. To ﬁnd out which detector is the most

complementary with HA and ε = 3, for instance, look at the

HA row and column (here in blue). It shows that it is HEL.

For each detector and each ε value, the best result appears

in bold.

BE FA HAL HA HEL KA KR MO SI SR

17 0

4 0

HAL

20 9 0

2 1 0

55 28 15 0

2 2 0 0

HEL

58 56 9 67 0

10 10 0 6 0

56 28 40 56 49 0

19 12 9 9 15 0

58 18 23 62 73 58 0

8 2 1 1 9 20 0

39 4 39 42 53 85 27 0

2 0 8 10 5 27 1 0

37 28 16 56 58 45 51 31 0

7 3 1 2 10 20 5 2 0

23 13 70 25 3 38 26 46 10 0

3 1 8 1 0 9 2 12 1 0

42 6 36 42 55 92 33 45 32 39

3 0 3 1 6 30 2 3 3 5

Table 3: Contribution measures taking into account the re-

peated feature points (see table 2 for notations).

BE FA HAL HA HEL KA KR MO SI SR

18 0

6 0

HAL

19 7 0

2 1 0

52 30 12 0

3 3 0 0

HEL

61 51 8 75 0

13 12 1 6 0

34 19 71 33 32 0

17 14 11 7 16 0

68 17 22 60 72 42 0

9 2 1 1 11 22 0

46 5 36 44 55 82 35 0

2 0 10 0 6 31 1 0

42 27 15 67 63 29 53 34 0

8 4 1 2 13 21 6 2 0

21 9 85 20 3 64 24 42 8 0

3 1 12 1 0 11 2 13 1 0

42 5 43 36 47 85 35 62 29 41

3 1 3 1 7 37 2 3 3 5

score of 86+6.14=92.14% for the union HA+BE.

Analysis. These results can be read in two ways: (i)

for each detector they give which detector is the most

complementary in terms of contribution, repeatability

and spatial distribution ; (ii) they give the most com-

plementary detectors between them. The best com-

promises between repeatability and distribution are

given by: Harris, FAST and SIFT. Table 6 summa-

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

338

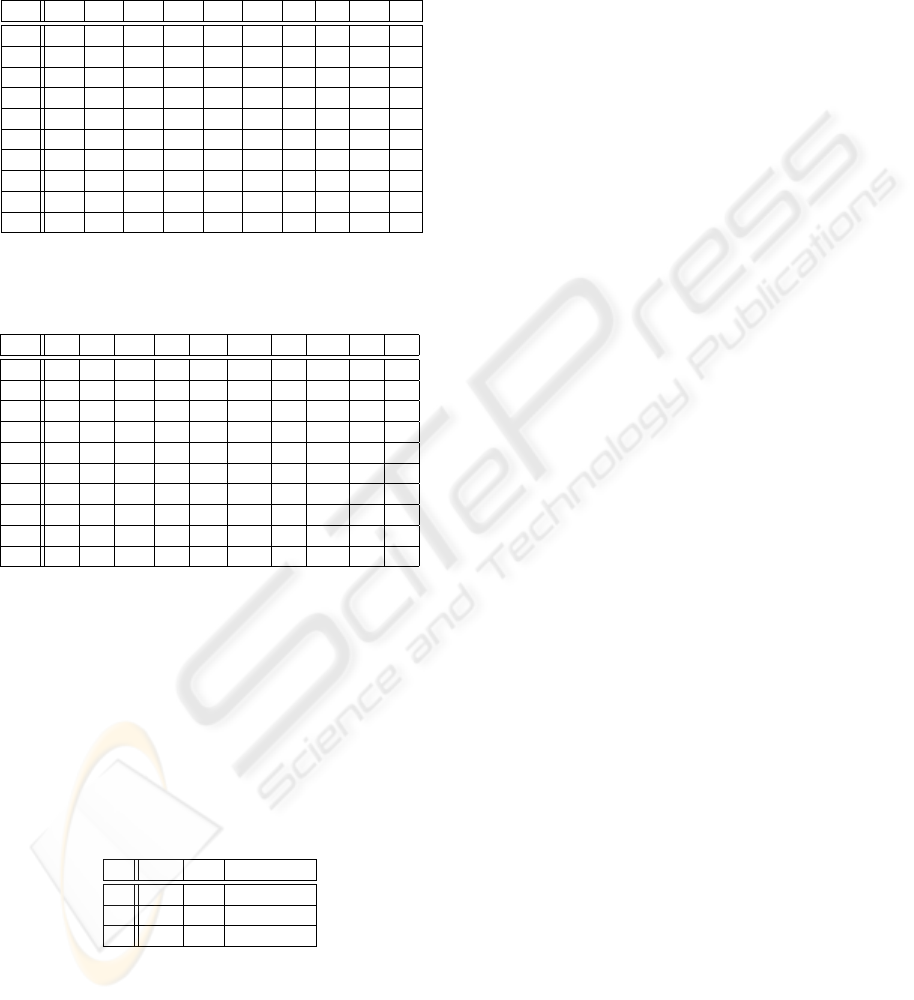
Table 4: Repeatability gain. For each couple of detectors

, we show gain

rep

(ε = 3). To determine which

detector is the most complementary in terms of repeatability

with HA, for instance, look at the HA row and column (here

in blue), it shows that it is HEL. For each detector, the best

result appears in bold.

BE FA HAL HA HEL KA KR MO SI SR

FA 1.55 0

HAL 0.75 -0.36 0

HA 3.77 0.32 -0.36 0

HEL 4.48 2.12 0.36 4.20 0

KA -0.17 -1.69 -0.39 -0.38 2.03 0

KR 4.71 0.22 0.90 3.88 5.75 1.81 0

MO 3.78 -0.69-0.62 3.11 4.47 -1.34 2.83 0

SI 3.57 1.19 0.76 3.40 2.37 0.82 4.98 3.00 0

SR 1.01 0.38 0.09 0.66 -2.06 1.48 1.70 0.82 -0.19 0

SU 3.53 -1.21 1.65 2.24 5.00 2.60 3.50 2.23 2.46 2.63

Table 5: Distribution gain. For each couple of detectors

, we show gain

,S2

(ε = 3) (see 4 for an exam-

ple of how to read the table).

BE FA HAL HA HEL KA KR MO SI SR

FA 3.96 0

HAL 2.23 1.30 0

HA 6.14 5.11 1.19 0

HEL 8.13 7.80 1.30 6.09 0

KA 8.53 6.85 7.09 5.54 9.27 0

KR 6.47 4.23 3.28 5.86 7.98 6.08 0

MO 3.82 0.02 6.46 3.26 8.62 12.07 2.30 0

SI 5.32 4.96 1.52 5.95 5.39 6.88 6.12 2.92 0

SR 4.15 3.79 4.89 3.63 0.51 11.58 5.30 10.38 1.71 0

SU 6.16 0.10 3.30 4.18 9.72 10.17 3.20 3.27 4.45 7.12

rizes the most complementary detectors to the detec-

tors in terms of contribution, repeatability and region-

wise distribution. The most complementary detectors

between them are Kadir and SUSAN, Kitchen and

Rosenfeld and Hessian-Laplace, Moravec and Kadir

i.e. they return the most distinct sets of feature points.

Table 6: This table summarizes the most complementary

detectors to Harris, FAST and SIFT in terms of contribution

(Cont.) (ε = 3) (results are similar whether all the feature

points or only the repeated points are taken into account),

repeatability (R) and region based distribution (RD

D Cont. R RD

,S2

HA HEL HEL BE

FA HEL HEL HEL

SI HEL KR KA

6 CONCLUSIONS

We proposed an evaluation and a comparison of

eleven well-known feature point detectors based on

new criteria used to characterize spatial distribution

and complementarity. This study aims to be helpful

for any applications that need feature points well dis-

tributed in the image. It also helps to select the most

complementary detectors in terms of region based dis-

tribution. This work will be extended on larger trans-

formations between the images.

REFERENCES

Bay, H., Ess, A., Tuytelaars, T., and Gool, L. V. (2006).

SURF: Speeded up robust features. CVIU, pages 346–

359.

Beaudet, P. R. (1978). Rotationally invariant image opera-

tors. In ICPR, pages 579–583, Kyoto, Japan.

Gil, A., Martinez, O., Ballesta, M., and Reinoso, O. (2009).

A comparative evaluation of interest point detectors

and local descriptors for visual SLAM. MVA.

Harris, C. and Stephens, M. (1988). A combined corner

and edge detector. In Alvey Vision Conference, pages

147–151, Manchester, United-Kingdom.

Hartley, R. I. and Zisserman, A. (2004). Multiple View Ge-

ometry in Computer Vision. Cambridge University

Press, ISBN: 0521540518, second edition.

Kadir, T., Zisserman, A., and Brady, M. (2004). An afﬁne

invariant salient region detector. In ECCV, pages 404–

416, Prague, Czech Republic.

Kitchen, L. and Rosenfeld, A. (1982). Gray level corner

detection. PRL, 1(2):95–102.

Lhuillier, M. and Quan, L. (2002). Match propagation

for image-based modeling and rendering. PAMI,

24(8):1140–1146.

Lowe, D. G. (1999). Object recognition from local scale-

invariant features. In ICCV, volume 2, pages 1150–

1157, Kerkyra, Greece.

Mikolajczyk, K., Leibe, B., and Schiele, B. (2005). Local

features for object classe recognition. In ICCV, vol-

ume 2, pages 1792–1799, Beijing, China.

Mikolajczyk, K. and Schmid, C. (2004). Scale & afﬁne

invariant interest point detectors. IJCV, 60(1):63–86.

Moravec, H. P. (1977). Toward automatic visual obstacle

avoidance. In IJCAI, volume 2, pages 584–584, Mas-

sachusetts, USA.

Noble, J. A. (1988). Finding corners. IVC, 6(2):121–128.

Rosten, E. and Drummond, T. (2006). Machine learning

for high-speed corner detection. In ECCV, volume 1,

pages 430–443, Graz, Austria.

Schmid, C., Mohr, R., and Bauckhage, C. (2000). Evalua-

tion of interest point detectors. IJCV, 37(2):151–172.

Shi, J. and Tomasi, C. (1994). Good features to track. In

CVPR, pages 593–600, Seattle, USA.

Smith, S. M. and Brady, J. M. (1997). Susan – a new ap-

proach to low level image processing. IJCV, 23(1):45–

78.

COMPLEMENTARITY OF FEATURE POINT DETECTORS

339