ADAPTIVE PATCH-BASED INPAINTING FOR IMAGE BLOCK

RECOVERY

Yunqiang Liu

Barcelona Media - Innovation Center, University of Pompeu Fabra, Barcelona, Spain

Jin Wang, Huanhuan Zhang

Philips Research Asia - Shanghai, China

Keywords:

Image block recovery, Inpainting, Error propagation, Combination strategy.

Abstract:

This paper presents an adaptive patch-based inpainting algorithm for image block recovery in block-based

coding image transmission. The proposed approach is based on prior information - patch similarity within

the image. By taking advantage of the information, we recover the lost pixels by copying pixel values from

the source based on a similarity criterion to keep local continuity. The pixel recovery is performed in a

sequential fashion in which the recovered pixels can be used in the recovery process afterwards. In order

to alleviate the error propagation with sequential recovery, we proposed an adaptive combination strategy

which merges different directional recovered pixels according to the conﬁdence of the estimated recovery

performance. Experimental results show that the proposed method provides signiﬁcant gains in both subjective

and objective measurements.

1 INTRODUCTION

With the advent of multimedia communication, im-

age/video transmission is becoming more and more

important. Unfortunately, transmission error is in-

evitable on most channels such as wireless channels

and the Internet which are not reliable enough to

guarantee error-free transmission. Meanwhile, exist-

ing multimedia compression standards such as JPEG,

MPEG-2 and H.264 (Sullivan and Wiegand, 2005)

use the variable length coding (VLC) with block-

based structure. The bit stream encoded by those stan-

dards is very sensitive to transmission errors (Kung

et al., 2006). Even one single bit error may cause the

loss of a whole block. And in video transmission, the

mistakes in current blocks even propagate to the fol-

lowing blocks or the following frames, which will re-

sult in serious degradation in the visual quality of the

decoded image.

Error recovery as a post-processing module is

widely adopted to alleviate the negative effect of the

erroneous blocks (Wang and Zhu, 1998) which at-

tempts to reconstruct corrupted pixels utilizing the

available neighbor information, without modifying

source and channel coding schemes. Comparing to

other existing error resilient approaches (Wang et al.,

2000) as the Forward Error Correction and the inter-

active methods, no extra delay or redundant informa-

tion will be added to the bit stream.

In general, according to correlation information,

error recovery methods could be divided into two

classiﬁcations (Agraﬁotis et al., 2006): spatial error

recovery (SER) and temporal error recovery (TER).

The former utilizes spatial neighbor information to ﬁll

the missing area whereas the latter utilizes temporal

information from successive frames. The spatial er-

ror recovery is often adopted in image sequence, intra

coded frame and areas of low temporal redundancy in

inter-coded frame.

A number of spatial recovery approaches have

been proposed already in the literature. Bilinear inter-

polation (Wang et al., 2002) is a simple and efﬁcient

method which utilizes the nearest correctly decoded

pixels to reconstruct the lost areas with weighted av-

erages of these pixels. Rane et al. (Rane et al., 2002)

estimate the lost information in the frequency domain

based on the spatial smoothing constraint on the re-

constructed blocks. While the obtained results are

fairly good, these algorithms provide smooth recon-

structions in image regions. Several methods try to

Liu Y., Wang J. and Zhang H. (2010).

ADAPTIVE PATCH-BASED INPAINTING FOR IMAGE BLOCK RECOVERY.

In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 52-59

DOI: 10.5220/0002832000520059

 SciTePress

mitigate this problem by interpolating missing pixels

along estimated edge directions such as directional in-

terpolation (Kim et al., 2006) and verge points based

method (Gao et al., 2007). In (Hong et al., 1999),

error recovery is performed recursively for bands of

missing pixels, using border pixels of surrounding

blocks and already concealed pixels of the recovered

block. The concept of sequential error recovery is also

followed in the orientation adaptive sequential inter-

polation (OASI) approach (Li and Orchard, 2002).

Some methods address the problem of recovering

missing data from different point of view. The best

neighborhood matching (BNM) method (Wang et al.,

1998) exploits block wise similarities within an image

to replace whole missing blocks through a search pro-

cess in the vicinity. Texture inpainting method, trig-

gered in part by texture synthesis (Efros and Leung,

1999), has shown promising results on restoring cor-

rupted image data, which is based on the similarity

between their local neighborhood and the surround-

ing neighborhoods. Criminisi et al. (Criminisi and

Perez, 2003) present an order-based image inpainting

method that extends the texture synthesis approach by

imposing higher priorities in the restoration order for

pixels lying in the neighborhood of edges, thereby

preserving better edge sharpness and continuity. In

(Arias et al., 2009) the authors propose a non-local

variational model to address the texture-oriented in-

painting problem and provide impressive results. In

(Bertalmio et al., 2003) Bertalmio et al. decompose

the image into two functions, one for the texture in-

gredient and the other for the geometry structure of

the image. Then they ﬁll in the texture component

using texture synthesis, and ﬁll in the structure part

using a classical inpainting approach based on partial

differential equation models (Bertalmio et al., 2000)

(Chan and Shen, 2001).

This paper presents an adaptive patch-based in-

painting algorithm for image block recovery in block-

based coding image transmission. The proposed ap-

proach is based on prior information - patch similarity

within the image. By taking advantage of this infor-

mation, we recover the lost pixels by copying pixel

values from the source based on a similarity criterion

to keep local continuity. The pixel recovery is per-

formed in a sequential fashion in which the recovered

pixels, as well as the uncorrupted pixels in the neigh-

bor area, can be used in the recovery process after-

wards. In order to alleviate the error propagation with

sequential recovery, we proposed an adaptive com-

bination strategy to reconstruct the lost block, which

merges different directional recovered pixels accord-

ing to their conﬁdence. The conﬁdence is estimated

by the dissimilarity and the amount of reliable infor-

mation in the patch.

The remainder of this paper is structured as fol-

lows. In Section 2, we give an overview of the

proposed adaptive patch-based inpainting algorithm.

Section 3 presents the proposed method in detail. Sec-

tion 4 gives the results and comparisons, and conclu-

sions are drawn in Section 5.

2 ALGORITHM OVERVIEW

Before the application of our image recovery ap-

proach, it is assumed that that we can locate the error

region in the decoded video or image with some

error detection algorithms. Most of traditional error

recovery methods, such as bilinear interpolation,

directional interpolation and OASI, perform as a low

pass ﬁlter or directionally low pass ﬁlter in nature.

They cannot recover accurately the sharp edge and

texture within the lost region, however, the edge and

texture information is very important for the human

vision system. It is introduced by the following two

reasons (Wang et al., 1998). First, the information

source to estimate pixels in the missing blocks is the

neighboring pixels in a very limited local region.

Second, these methods rely on some predeﬁned

constraints on the lost blocks such as the recovered

blocks should be smoothly connected with adjacent

regions either in spatial or in transform domain.

(a) (b)

Figure 1: Textural and edge images.

ADAPTIVE PATCH-BASED INPAINTING FOR IMAGE BLOCK RECOVERY

In order to overcome the above problems, the BNM

method exploits block wise similarities within an im-

age to replace whole missing blocks through a search

process in not only neighboring regions, but also re-

mote regions within the image. The method can re-

construct the simple texture block (Figure 1(a)) and

single strong edge (Figure 1(b)) effectively, and it can

keep the sharp edge and details of texture in the lost

block. However, BNM fails to recover the region with

multiple edges (Figure 1(c)) or complex texture (Fig-

ure 1(d)), because there are much less matching pos-

sibilities for the lost blocks in the image. The BNM

method takes the missing block as a whole to ﬁnd a

similar area in the vicinity. When the missing block

is large, such as 8x8 or 16x16 which is very common

in block-based image-coding systems, it is very difﬁ-

cult to ﬁnd the similar area especially for the situation

in Figures 1(c) and 1(d). Based on this observation,

we adopt the approach of patch-based inpainting to

reconstruct the missing regions. The approach grows

the missing area pixel by pixel, based on prior infor-

mation - patch-wise self-similarity within the image.

By taking advantage of the information, we recover

the lost pixels by copying pixel values from the source

based on a similarity criterion to keep local continu-

ity. The pixel recovery is performed in a sequential

fashion in which the recovered pixels, as well as the

uncorrupted pixels in the neighbor area, can be used

in the recovery process afterwards (Li and Orchard,

2002). This sequential fashion introduces a bias on

the later recovered pixels. Because the later recovered

pixels depend on the previous recovered pixels, error

propagation is inevitable. The quality of the recovered

image is highly inﬂuenced by the order in which the

ﬁlling process proceeds. The pattern of error prop-

agation varies with the recovery order. In order to

alleviate the error propagation with sequential recov-

ery, we perform the patch-based inpainting algorithm

from different directions. Then we calculate the con-

ﬁdence of the interpolated pixels from different direc-

tions, and ﬁnally combine them by adaptive weighting

according to the conﬁdence.

The proposed adaptive combination strategy is in-

spired by the work in (Li and Orchard, 2002). The

authors adopt a linear merge strategy, in which the

weights only depend on the distances of the given

pixel to the four borders of the block. These distances

cannot fully reﬂect the contribution of the pixels from

different directions to the interpolated pixel. In our

method, we introduced two conﬁdence measurements

to evaluate the contribution: reliability conﬁdence

and similarity conﬁdence. The former measures the

amount of the reliability of the available pixels for

recovering the missing one. The latter evaluates the

Figure 2: Reconstruction of lost blocks.

quality of the contribution of the available pixels to

the interpolated pixel. And the ﬁnal weights are deter-

mined by the two conﬁdence measurements together.

Based on the above analysis, the reconstruction of lost

blocks follows three main steps:

a) Choose the scan direction as recovery order;

b) Patch-based inpainting for each determined di-

rection;

c) Merge them by adaptive weighting according to

the conﬁdence.

3 ADAPTIVE PATCH-BASED

INPAINTING

In the proposed adaptive patch-based inpainting al-

gorithm, we ﬁrst determine the recovery order for

single-directional pixel interpolation. For each deter-

mined recovery order, we then recover the missing

block using patch-based inpainting algorithm based

on patch-wise similarity within the image. Finally,

we reconstruct the missing block by an adaptive com-

bination strategy according the conﬁdence of the in-

termediate recovered pixels. A sketch map of the pro-

cedure of our method is shown in Figure 2.

3.1 Recovery Order

For single directional error recovery, error propaga-

tion is inevitable because the later recovered pixels

depend on the previous recovered pixels. Different

recovery orders may introduce different error propa-

gation patterns. In practice, a speciﬁc recovery order

is very effective for its speciﬁc area and direction of

edge in the image. For example, the raster scanning

order from left to right can reconstruct the horizontal

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

edge more accurately than the vertical edge. More-

over, the pixels in the top-left area can be recovered

more accurately that those in the bottom-right area.

Single order recovery cannot represent the correct and

acceptable result especially for the area with complex

structure. Each recovery order has its own advantage

on its speciﬁc area and direction of edge in the im-

age. Therefore, it is expected that we can reconstruct

the image with high quality after carefully merging

the result from different recovery order, as shown in

Figure 2. Theoretically, if there are K continuous cor-

rupted pixels, there are K! different orders to get K!

recovery results(Li and Orchard, 2002). The compu-

tation is tremendous complex for searching all the or-

ders. In fact, lots of recovery orders are not practical.

For example the recovery beginning from the center

of the corrupted areas has little available information.

It is reasonable to choose several typical orders. In

this way, the reconstructed quality doesn’t decrease so

much whereas the computation complexity decreases

signiﬁcantly. In our method, we use raster recovery

order due to its simplicity of implementation. Starting

from each corner, there are two directions to reach the

diagonal corner and traversal all the missing pixels.

Therefore, we adopt eight single-directional recovery

orders, which is introduced by X. Li et al. the detailed

information can be found in (Li and Orchard, 2002).

Take the top-right corner as an example as shown in

Figure 3, the recovery process starts from the pixels in

the top-right corner, there are two directions to reach

the diagonal corner. In Figure 3(a), it recovers the

missing pixels with the direction from right to left for

each line and repeats the process till the bottom-left

corner. The missing block will be recovered using

patch-based inpainting in each determined direction.

3.2 Patch-based Inpainting

For each determined recovery order, the patch-based

inpainting algorithm uses patch-wise similarity within

the image to reconstruct the missing block.

The missing block is referred to as the unknown

area, denoted by Ω. The area will now be ﬁlled, pixel

by pixel, in a raster fashion. The known area, denoted

by Φ, provides samples used in the ﬁlling process. Let

Ψ denote the patch. The patch may be a square, rect-

angle, triangle, or any other shape, and all the pixels

within the patch are contiguously connected.

In this paper, the patch centered at the pixel p

(i, j) is here deﬁned to be a diamond shaped window,

as:

Ψ(p

) = {p = (x, y), 0 ≤ (|x−i| + |y− j|) ≤ T

} (1)

where T

is the order of the patch, which controls

the size of the patch. A target patch with T

= 2 is

shown in Figure 4, where the light-gray pixel p is the

current pixel to be recovered, and the dark-gray pixels

represent the available pixels, available means uncor-

rupted or recovered, the white pixels are the missing

pixels. A source patch is the corresponding area in Φ,

which has the same shape and size as the target patch.

(a) (b)

Figure 3: Textural and edge images.

To recover the lost pixels, a search procedure is

applied within a large range in the image. The pur-

pose of the search procedure is to ﬁnd a source patch

in the image that has the best similarity with the target

patch. We then replace the current pixel being ﬁlled in

the lost block by the value of the corresponding pixel

of the best matched source patch, as shown in Figure

5. Then we recover the rest of pixels using the same

approach under the mentioned recovery order.

Figure 4: Target patch with the order of 2.

The similarity of the source patch and the target

patch is measured by the normalized sum of absolute

differences. Since it is desirable to give more impor-

tance to the pixels that are uncorrupted than those re-

covered previously, different weights are taken for the

two kinds of pixels. The pixels within the patch that

have not been recovered yet are not taken into account

in the distance. The distance between the source patch

and target patch can thus be expressed as:

ADAPTIVE PATCH-BASED INPAINTING FOR IMAGE BLOCK RECOVERY

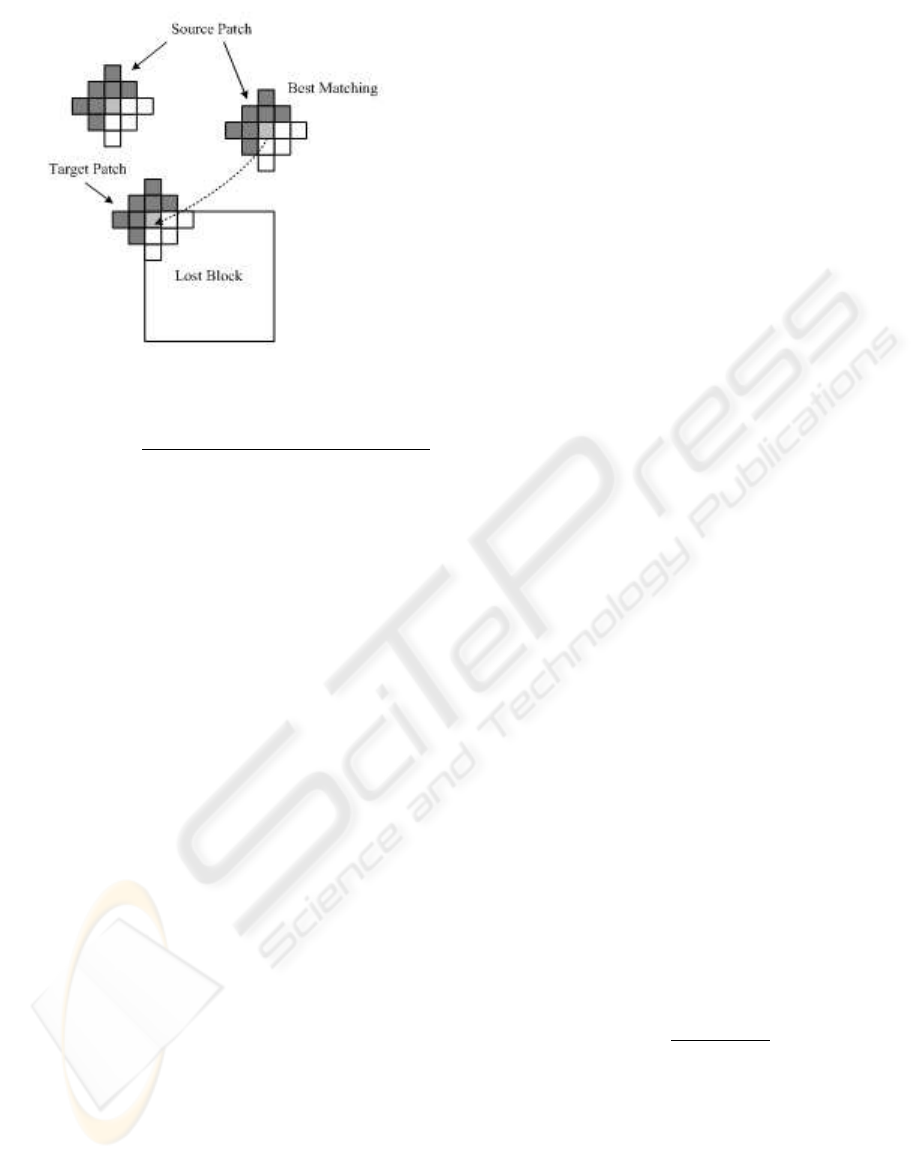
Figure 5: Pixel recovery.

d(Ψ(p

), Ψ(p

)) =

∑

q∈Ψ(q

)

a(p

+ q)| f(p

+ q) − f(p

+ q)|

∑

q∈Ψ(q

)

a(p

+ q)

(2)

where p

and p

are the centers of the source patch

Ψ(p

) and the target patch Ψ(p

), respectively, f (p)

is the value of the pixel p, Ψ(q

) is the diamond win-

dow deﬁned in (1) and q

= (0, 0), The weight map

a(p) is assigned for each pixel in target patch, as fol-

lows:

a(p) =







1, p is uncorrupted

0.5, p is revcovered

0, p is lost

(3)

The recovered pixel has some distortion and is

given a lower weight compared with the uncorrupted

one. And a(p) is set to 0.5 for the recovered pixel,

experimentally.

In summary, the patch based inpainting algorithm

for single directional recovery proceeds as follows:

1. Choose a pixel to be recovered in Ω as current

pixel according to the predetermined recovery or-

der, such as that in Figure 3(a).

2. Get the target patch Ψ(p

) centered by the cur-

rent pixel, and search as the best matching

source patch Ψ(p

) with Ψ(p

) , which minimizes

d(Ψ(p

), Ψ(p

)). In this paper, the search range is

selected as 32× 32.

3. Copy the pixel in the center of the source patch to

the current pixel. Alternatively, in order to accel-

erate the computation, we can ﬁll all the unknown

pixels in the target patch by the corresponding

pixels in the source patch. In this case, the com-

putation will be decreased signiﬁcantly with ac-

ceptable reduction of the performance.

4. Repeat steps 1, 2, and 3 until all the lost pixels are

ﬁlled.

3.3 Combination Strategy

In single-directional inpainting, the error of restored

pixels will increase along the recovery direction be-

cause of unconﬁdent recovered pixel results. Dif-

ferent recovery orders may introduce different error

propagation patterns. The error from one recovery or-

der can be compensated by results from the other or-

der. Therefore, we can reconstruct the image through

merging the result from different recovery orders as:

p =

∑

n=1

(p) f (p

) (4)

where w

(p) is the weighting coefﬁcient control-

ling the contribution of the n

recovery order for the

pixel p, and f(p

) is the value of the recovered pixel

in the n

order.

In this paper, the weight is associated with the

conﬁdence of the recovery performance in a speciﬁc

recovery order. The conﬁdence consists two items:

similarity conﬁdence S

(p) and reliablility conﬁdence

(p).

The similarity conﬁdence S

(p) can be expressed

by the Gaussian function of the Euclidean distance

between the source patch and the target patch, and we

simpliﬁed it as:

(p) = 2

−αd

∗

(Ψ(p

),Ψ(p

))

(5)

where d

∗

(Ψ(p

), Ψ(p

)) is the difference between

the target patch and the best match source patch,

which is deﬁned in (2), and the parameter α regulates

the relative inﬂuence of the difference on the weights.

It is set to 0.125, experimentally.

The reliability conﬁdence R

(p) measures the

amount of reliable information surrounding the pixel

p. Our aim is to give higher weight to the pixel whose

patch has more pixels which are known or have al-

ready been recovered. R

(p) is deﬁned as:

(p) =

∑

q∈Ψ(p)

(q)

A(Ψ(p))

(6)

where Ψ(p) is the target patch centered on the

pixel p, A(Ψ(p)) is the area of the patch Ψ(p), i.e.

the number of pixels in the patch. Initially, we deﬁne

(p) = 0 if p is a missing pixel, R

(p) = 1 if not.

For each pixel p to be recovered, we deﬁne its

weight for a speciﬁc recovery order associated with

the product of above two terms:

(p) ∝ S

(p)R

(p) (7)

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

The weighting provides an efﬁcient and ﬂexible way

to select the appropriate pixels contributing to the es-

timation of the lost pixel for the ﬁnal result.

We compute the conﬁdence for all the recovery

order for each lost pixel, and normalize the weight

coefﬁcients as:

(p) =

(p)R

(p)

∑

k=1

(p)R

(p)

(8)

After obtaining these weight coefﬁcients, we recover

the lost pixels through combining the intermediate re-

sults from all the recovery orders.

4 EXPERIMENT RESULTS

In order to illustrate the performance of our error re-

covery method, we take many experiments on test im-

ages: Lena, Baboon, Pepper and Barbara. We con-

sider the situation of the 16× 16 block since the im-

age or video are often encoded in 16× 16 block size.

Different block-loss situations are investigated in the

paper: isolated block loss and consecutive block loss.

For objective evaluation, we use a modiﬁed peak

signal-to-noise ratio (PSNR) as the objective measure

in our experiments, which is deﬁned just on the cor-

rupted areas instead of the entire image:

PSNR = 10log

255

∑

p∈Ω

( f

(p) − f

(p))

(9)

where f

(p) and f

(p) are the pixel values in the

original and the recovered image, and M is the num-

ber of the lost pixels. We ﬁrst give the implementation

details in our experiments and then compare it with

several existing error recovery algorithms.

4.1 Implementation Details

For the implementation of the proposed algorithm,

there remain some choices, which include the follow-

ing:

1. The patch size. The size of the patch affects how

well the ﬁlled pixels capture the local characteris-

tics of the known region. The patch size is con-

trolled by T

, which is deﬁned in (1).

2. The ﬁlling manner. The ﬁlling manner means

whether the pixel centered on the target patch

(pixel-ﬁlling) or the unknown part of the target

patch (patch-ﬁlling) will be ﬁlled in the step 3 of

the patch based inpainting algorithm.

In the ﬁrst experiment, we illustrate how the choice

of patch size affects the recovery performance. We

ﬁx the search range as 32× 32 with pixel-ﬁlling. And

we investigate the isolated block loss situation with

about 10% loss rate. Table 1 shows the evolution of

PSNR values with different patch size using pixel-

ﬁlling. Smaller patch size allows more matching pos-

sibilities, thus implies weaker statistical constraints.

Up to a certain limit, bigger patch size can capture

the texture characteristics better, however with much

higher computation complexity. From the results in

Table 1, T

= 2 is a good balance.

Table 1: The impact of patch size for block loss (dB).

Lena Baboon Pepper Barbara

1 26.63 20.94 28.34 24.13

2 27.35 21.25 29.10 26.01

3 27.33 21.24 29.31 26.40

Table 2: The impact of patch size for block loss (dB).

Filling Lena Baboon Pepper Barbara

Pixel 27.35 21.25 29.10 26.01

Patch 27.06 20.88 28.12 25.94

Table 3: Performance comparison for isolated block loss

(dB).

Image BI OI OASI Ours

Lena 24.03 23.74 25.98 27.35

Baboon 20.25 18.46 20.16 21.25

Pepper 24.85 24.34 26.67 29.10

Barbara 20.69 21.62 22.84 26.01

In the second experiment, we demonstrate the im-

pact of the ﬁlling manner on the recovery perfor-

mance. Table 2 shows the performance of the two

different ﬁlling manners with T

= 2. It can be seen

that pixel-ﬁlling shows better performance than the

patch-ﬁlling and the gap ranges from 0.07 to 0.98 dB.

4.2 Comparison Results

To demonstrate the effectiveness of our algorithm, we

compare it with several previous existing error recov-

ery algorithms: bilinear interpolation (BI), the ori-

entation adaptive sequential interpolation (OASI) (Li

and Orchard, 2002), order-based inpainting (OI) (Cri-

minisi and Perez, 2003). For our algorithm, in the

experiment, we set T

= 2 and use pixel-ﬁlling man-

ner in the recovery process.

Table 3 and Table 4 give the PSNR comparisons

between the compared methods and our algorithm

under the following two loss situations: the isolated

block loss (about 10%) and consecutive block loss

ADAPTIVE PATCH-BASED INPAINTING FOR IMAGE BLOCK RECOVERY

Table 4: Performance comparison for consecutive block

loss (dB).

Image BI OI OASI Ours

Lena 22.21 21.32 22.07 24.21

Baboon 19.15 17.94 19.08 20.24

Pepper 25.22 23.26 24.00 26.05

Barbara 19.98 18.21 20.06 23.11

(a) Origin (b) Corrupted

(e) OASI (f) Our Method

Figure 6: Reconstructed images for Barbara for isolate

block loss.

(about 25%). It can be seen that we have achieved

1.09-3.17 dB improvement in the case of isolated

block loss and 1.16-3.05 dB improvement in the case

of consecutive block loss over OASI. To subjectively

evaluate the results, Figure 6 shows the comparison

of the reconstructed images for Barbara by the com-

pared methods and our algorithm in the situation of

isolated block loss. It can be observed that our new

approach has achieved signiﬁcant improvements in

the area of complex texture structures. For better sub-

jective evaluation, we show some enlarged examples

for sharp edge areas, texture areas and very complex

areas in Figure 7. The visual quality of the recov-

(a) Bilinear Interpolation (b) Order-based Inpainting

Figure 7: Enlarged part of the images in Figure 6.

ered blocks are very good even when the areas con-

tain a lot of detail information. Figure 8 shows the

comparison of the reconstructed images for Lena by

the compared methods and our technique in the situa-

tion of consecutive block loss. Signiﬁcant improve-

ments can be found in the recovered image by the

proposed method, especially on the blocks with the

strong edges or complex texture. And the similar re-

sults are obtained for other test images.

5 CONCLUSIONS

In this paper, we present an adaptive patch-based in-

painting algorithm for image block recovery in block-

based coding image transmission. The proposed ap-

proach is based on a prior information - patch simi-

larity within the image. By taking advantage of the

information, we recover the lost pixels by copying

pixel values from the source based on a similarity cri-

terion to keep local continuity. The pixel recovery is

performed in a sequential fashion in which the recov-

ered pixels can be used in the recovery process after-

wards. In order to alleviate the error propagation with

sequential recovery, we proposed an adaptive combi-

nation strategy which merges different directional re-

covered pixels according to the conﬁdence of the es-

timated recovery performance. Experimental results

show that the proposed method provides signiﬁcant

improvements in terms of both subjective and objec-

tive evaluations.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

(a) Origin (b) Corrupted

(e) OASI (f) Our Method

Figure 8: Reconstructed images for Lena for consecutive

block loss.

ACKNOWLEDGEMENTS

The authors deeply appreciate the constructive sug-

gestions and insightful comments from Prof. Vicent

Caselles.

REFERENCES

Agraﬁotis, D., Bull, D., and Canagarajah, C. (2006). Error

resilient video coding techniques. IEEE Trans. Cir-

cuits Syst. Video Technol., 16(8):960–973.

Arias, P., Caselles, V., and Sapiro, G. (2009). Varia-

tional framework for non-local image inpainting. In

Proc.EMMCVPR, pages 345–358, Bonn, Germany.

Bertalmio, M., Sapiro, G., Caselles, V., and Ballester, C.

(2000). Image inpainting. In Proc. Computer Graph-

ics (SIGGRAPH 2000), pages 417–424.

Bertalmio, M., Vese, L., Sapiro, G., and Osher, S. (2003).

Simultaneous structure and texture image inpainting.

IEEE Trans. on Image Processing, 12(8):882–889.

Chan, T. and Shen, J. (2001). Mathematical models for

local nontexture inpainting. SIAM J. Appl. Math.,

62(3):1019–1043.

Criminisi, A. and Perez, P. (2003). Object removal by

exemplar-based inpainting. In Proc. Int. Conf. Comp.

Vision Pattern Rec., pages 721–728, Madison, WI.

Efros, A. and Leung, T. (1999). Texture synthesis by non-

parametric sampling. In Proc. Int. Conf. Computer

Vision, pages 1033–1038, Kerkyra, Greece.

Gao, Y., Wang, J., Liu, Y., Yang, X., and Wang, J.

(2007). Spatial error concealment technique using

verge points. In Proc. IEEE ICASSP, pages 309–312,

Honolulu, HI.

Hong, M. C., Scwab, H., Kondi, L., and Katsaggelos, A. K.

(1999). Error concealment algorithms for compressed

video. Signal Processing: Image Communication,

14:473–492.

Kim, W., Koo, J., and Jeong, J. (2006). Fine directional in-

terpolation for spatial error concealment. IEEE Trans.

Consumer Electronics, 52(3):1050–1055.

Kung, W.-Y., Kim, C.-S., and Kuo, C.-C. J. (2006). Spatial

and temporal error concealment techniques for video

transmission over noisy channels. IEEE Trans. Cir-

cuits Syst. Video Technol., 16:789–802.

Li, X. and Orchard, M. T. (2002). Novel sequential error-

recovery techniques utilizing orientation adaptive in-

terpolation. IEEE Trans. Circuits Syst. Video Technol.,

12(10):857–864.

Rane, S. D., Remus, J., and Sapiro, G. (2002). Wavelet-

domain reconstruction of lost blocks in wireless im-

age transmission and packet-switched networks. In

Proc.IEEE ICIP, pages 309–312, Rochester, NY.

Sullivan, G. J. and Wiegand, T. (2005). Video compression

- from concepts to the H.264/AVC standard. Proceed-

ings of the IEEE, 93(1):18–31.

Wang, Y., Hannuksela, M. M., Varsa, V., Hourunranta, A.,

and Gabbouj, M. (2002). The error concealment fea-

ture in the H.26L test model. In Proc. IEEE ICIP,

pages 729–732, Rochester, NY.

Wang, Y., Wenger, S., , and Katsaggelos, A. K. (2000). Er-

ror resilient video coding techniques. IEEE Signal

Processing Mag., 17(4):61–82.

Wang, Y. and Zhu, Q.-F. (1998). Error control and conceal-

ment for video communication: A review. Proceed-

ings of the IEEE, 86(5):974–997.

Wang, Z., Yu, Y., and Zhang, D. (1998). Best neighborhood

matching: An information loss restoration technique

for block-based image coding systems. IEEE Trans.

on Image Processing, 7(7):1056–1061.

ADAPTIVE PATCH-BASED INPAINTING FOR IMAGE BLOCK RECOVERY