LANE DETECTION BASED ON GUIDED RANSAC

Yi Hu, You-Sun Kim, Kwang-Wook Lee and Sung-Jea Ko

Center for Multimedia Communication & Processing, School of Electrical Engineering

Korea University, Anam-dong, Sungbuk-gu, Seoul, Korea

Keywords:

Driving assistance, Computer vision, Lane detection, RANSAC.

Abstract:

In this paper, a robust and real-time lane detection method is proposed. The method consists of two steps,

the lane-marking detection and lane model ﬁtting. After detecting the lane marking by the Intensity bump

algorithm, we apply the post ﬁlters by constraining the parallelism of lane boundary. Then, a novel model

ﬁtting algorithm called Guided RANSAC is presented. The Guided RANSAC searches lanes from initial

lane segments and the extrapolation of lane segments is used as the guiding information to elongate lane

segments recursively. With the proposed method, the accuracy of the model ﬁtting is greatly increased while

the computational cost is reduced. Both theoretical and experimental analysis results are given to show the

efﬁciency.

1 INTRODUCTION

In recent years, many driving assistance systems have

been developed. To increase driving safety, the basic

but important component is lane detection. With ac-

curate lane information, lane departure warning, lat-

eral control or impact warning can be achieved. In the

literature, various lane detection methods have been

proposed (Ieng et al., 2003; Kim, 2008; Wang and

Shen, 2004; Wu and Lin, 2007; Zhou et al., 2006).

Generally, the lane detection method consists of two

steps. The ﬁrst step is to detect lane-marking features

such as edge features (Wang and Shen, 2004; Zhou

et al., 2006), ridgel features (Lopez et al., 2005) or

intensity bump features (Ieng et al., 2003). Then in

the next step, for speciﬁc lane models, model param-

eters are estimated using the lane-marking features.

In most cases, the appearance of lane on the road im-

age is not straight line but curve. Thus, most popu-

lar lane models are using polynomial based models to

represent lane curves as (Kim, 2008; Wang and Shen,

2004; Zhou et al., 2006). A good survey can be found

in (McCall and Trivedi, 2006). The Hough transform

is a good estimator working on simple models such

as straight line or circle. As an adaptation, in (Wang

and Shen, 2004), the image is divided into severalsec-

tions so that lane segments in each section are approx-

imated as straight line segments. Then, Hough trans-

form is applied on each section. To estimate spline

curves, RANSAC is preferred. The author in (Kim,

2008) used an modiﬁed one to detect multiple lanes.

They generate a ﬁxed number of hypotheses and then

verify using inliers support and constrains. Here we

denote this method as substandard RANSAC to dif-

ferentiate from standard one. It is important to note

that the substandard RANSAC neither guarantees to

achieveoptimal solutions nor to ﬁnd all possible mod-

els. In this paper, we propose a novel lane model ﬁt-

ting algorithm called Guided RANSAC. It searches

all possible lanes by an iterative search strategy and

achieves optimal solutions with expected conﬁdence.

The rest of paper is organized as follows: Section 2

gives the description of lane-marking detection and

ﬁltering. Section 3 describes the Guided RANSAC

algorithm. In Section 4, theoretical analysis on com-

putational complexity is given. Then, Section 5 shows

the experimental results and Section 6 gives conclu-

sion.

2 LANE-MARKING DETECTION

For lane-marking detection, various algorithms have

been proposed. Among the existing techniques,

the intensity bump algorithm (Ieng et al., 2003) is

adopted in the proposed technique. To reduce the

false detections, a ﬁlter is introduced based on the fact

457

Hu Y., Kim Y., Lee K. and Ko S. (2010).

LANE DETECTION BASED ON GUIDED RANSAC.

In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 457-460

DOI: 10.5220/0002832204570460

 SciTePress

that the two boundaries of the lane are parallel. Af-

ter intensity bump detection, we calculate ﬁrst deriva-

tive of left and right boundary for each lane-marking

candidate: {dx

,dy

,dx

,dy

}. Then directions of left

and right boundary are calculated as: v

= R

· [x

]

and v

= R

· [x

]

. Then the lane-marking candi-

dates are ﬁltered using the rule as: v

· v

> τ, where

and R

are 2x2 matrix that to rotate edge orienta-

tions to boundary directions, τ is the threshold for the

boundary correlation.

3 LANE DETECTION METHOD

After the lane-marking detection, the detected results

are grouped to form meaningful structures such as

lines or curves. The popular approaches use poly-

nomial models with RANSAC as model ﬁtting algo-

rithm (Kim, 2008; Wang and Shen, 2004; Lopez et al.,

2005). We follow this framework and present a new

model ﬁtting algorithm to achieve lane detection ef-

ﬁciently. To extend the generalization of curve rep-

resentation, the lane is represented by multiple lane

segments. To represent one lane segment, we follow

Kim’s method (Kim, 2008) to use the cubic spline

model.

3.1 Guided RANSAC Algorithm

Conventionally, RANSAC method works on whole

sample space. For example, Kim’s method performs

lane ﬁtting on the whole sample space (Kim, 2008).

Here in this paper, a novel method is presented to

ﬁt the lane model in an iterative way. This method

is inspired by the CHEVP algorithm described in

(Wang and Shen, 2004). The CHEVP algorithm di-

vides the image into several horizontal sections and

lane segments are detected section by section. In-

stead of using explicit sections, we detect lane seg-

ments and elongate them recursively. The algorithm

is designed hierarchically as a main routine and a core

routine. The main routine scans all lane-markings se-

quentially. Once it ﬁnds an unvisited lane marking,

the core routine is activated to search a lane from a

starting lane-marking then iteratively search forward

to elongate the lane (see Figure 1). The core routine

mainly consists of two steps, a start search step and

an iterative search step. The start search step is to

ﬁnd an initial lane segment. Once an initial lane seg-

ment is found successfully, the iterative search step is

activated to elongate the lane segment as long as pos-

sible. In the start search step, lane-markings which

located near the starting lane-marking are collected

as a search space. The initial lane segment is approx-

imated as a straight line. RANSAC is performed to

ﬁnd the initial lane segment. In the iterative search

step, the lane-markings that close to the extrapolated

lane segment are gathered into a subset as the search

space. The idea is that lane markings located near the

extrapolated curve are more likely to lie on the lane.

It can be considered as a prediction of lane path. To

do the elongation, three control points are used during

the RANSAC ﬁtting. One control point is randomly

sampled from the search space while the other two

are directly from the previous lane segment. There

are several advantages of this scheme. First, it avoids

the unexpected elongation since the curve should pass

through two control points of the previous lane seg-

ment. Second, the number of iterations during the

RANSAC can be reduced since the search space is

small and only one sample is drawn randomly.

Figure 1: Core routine of Guided RANSAC. Lane is elon-

gated step by step.

3.2 Lane Segment Aggregation

The Guided RANSAC algorithmattempts to detect all

lane segments. One possible case is that dashed lane

segments are detected separately. We try to aggre-

gate lane segments to form lanes. The lane segments

are aggregated using a method similar to hierarchical

clustering. Iteratively, two lane segments are merged

into one using a merging function. The Figure 2 illus-

trates the use of the merging function. It generates a

hypothesis by selecting three control points from two

lane segments. Then the consistency of tow lane seg-

ments are evaluated. Short lane segments are thresh-

old out by lane-marking support.

4 THEORETICAL ANALYSIS

The standard RANSAC algorithm mainly consists of

two steps: 1) hypothesis generation and 2) hypothe-

sis veriﬁcation. The computational cost of standard

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

458

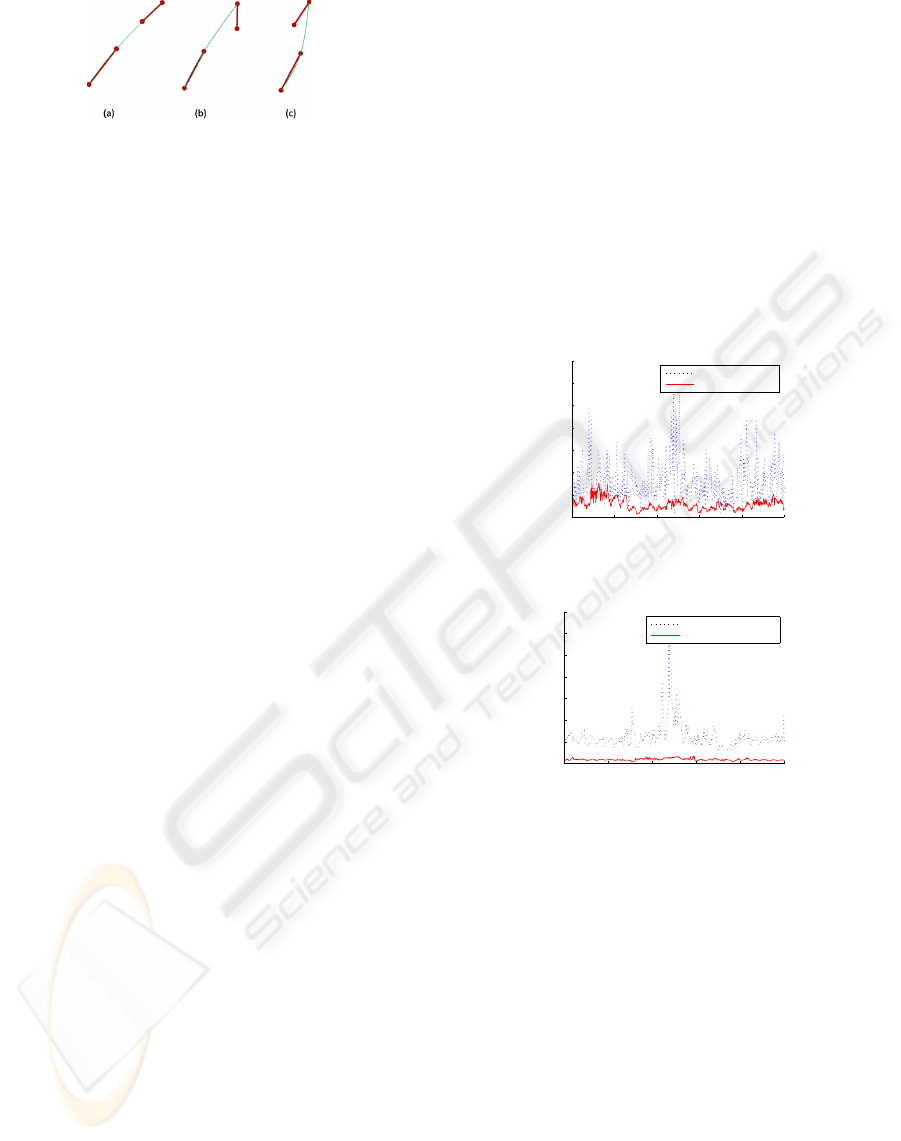
Figure 2: The merging function generates a hypothesis to

merge segments. (a) can be merged. (b) and (c) cannot be

merged.

RANSAC depends on the number of iterations and

the population of the sample space to perform con-

sensus veriﬁcation which can be expressed as a func-

tion linear to k∗ N, where N is the population, k is the

number of iterations which depends on stopping cri-

terions. One typical criterion is the probability of bad

model support after k iterations. Let w be the frac-

tion of inliers, m be the number of points needed to

generate hypothesis. Then the probability that no cor-

rect hypothesis is generated after k iterations will be:

p = (1− w

)

. We have the conﬁdence (1− p) to ob-

tain a good solution. Given p, k can be calculated

as: k = log(p)/log(1− w

). In order to ﬁnd multi-

ple models, a substandard RANSAC is used in (Kim,

2008) that a ﬁxed number of hypotheses is generated.

The problem is that a ﬁxed number of hypotheses

can neither guarantee an optimal solution nor sup-

port all models. The Guided RANSAC solves the

above problems since it searches all possible lanes.

The Guided RANSAC can be considered as a set of

standard RANSACs. The computational cost can be

roughly expressed as:

T ∝

∑

i=1

· k

) · δ(vis

= 0), (1)

where S is the size of subset in a search region and vis

stands for the visit state of samples. As described in

Equation 3, k depends on the value of p, w and m. p

is a predeﬁned parameter. w is the fraction of inliers

given by user. m is 1 in Guided RANSAC as given in

section 3.2. In contrast, 3 or 4 control points are re-

quired using standard RANSAC. In a typical setting

that p is 0.05 and w is 0.3, then log(p)/ log(1−w

) =

368.3 while log(p)/log(1 − w) = 8.4. It is promis-

ing that only few trials are required in our algorithm.

Furthermore, in each iterative search step, the search

space is restricted, so that S ≪ N and w is generally

increased. Finally, T becomes a quite small value. In

worst case, T = N ∗ S ∗ log(p)/log(1− w) where im-

age is total clutter. The additional computational cost

in Guided RANSAC is to generate subset. However,

the experimental results show that it is negligible.

5 EXPERIMENTAL RESULTS

The algorithm has been tested on image sequences

captured from real environment. The size of an im-

age is 720x480. First, we give the comparison re-

sult of standard RANSAC and proposed algorithm in

Figure 3. In this comparison, the standard RANSAC

uses 4 control points and both standard RANSAC

and Guided RANSAC use a bad model support cri-

terion with p = 0.05. The result shows that the com-

putational cost of our proposed algorithm is about 3

times less than standard RANSAC. We also found that

the real time cost of standard RANSAC and Guided

RANSAC are closely proportional to this result.

0 100 200 300 400 500

2000

4000

6000

8000

10000

12000

14000

frame index

number of evaluation

Standard RANSAC

Guided RANSAC

Figure 3: The comparison of computational cost.

0 100 200 300 400 500

frame index

time cost / ms

Substandard RANSAC

Guided RANSAC

Figure 4: The comparison of time cost.

In Figure 4, the comparison result between sub-

standard RANSAC and Guided RANSAC is given.

100 hypotheses are generated with 4 control points

as in (Kim, 2008). The reason of the peak time cost

of substandard RANSAC is that in a complex envi-

ronment, more outliers will lead to higher probability

to generate bad hypothesis. The average time cost of

Guided RANSAC is about 6 times less than substan-

dard RANSAC. Finally, we show the results on real

road images. In Figure 5, The lane aggregation con-

nects dashed lane or broken lane while removes false

positives. The results in Figure 6 show that the pro-

posed algorithm is robust to complex lane types such

as curved lane, dashed lane and crotched lane.

LANE DETECTION BASED ON GUIDED RANSAC

459

Figure 5: Lane aggregation. The ﬁrst row: without lane aggregation. Second row: with lane aggregation.

Figure 6: Detection results for complex lanes.

6 CONCLUSIONS

We have presented a novel method to detect lanes in

real-time. The algorithm requires little assumption

and is able to detect lanes in complex road conditions.

The experimental result shows that the proposed al-

gorithm is suitable for real-time applications such as

lane departure warning system. It can be extended to

many model ﬁtting based applications such as curve

ﬁtting, shape detection and so on.

ACKNOWLEDGEMENTS

This research was supported by Seoul Future Con-

tents Convergence (SFCC) Cluster established by

Seoul R&BD Program (No. 10570). This work

was supported by the Korea Science and Engineer-

ing Foundation(KOSEF) grant funded by the Korea

government(MEST) (No. 2009-0080547).

REFERENCES

Ieng, S.-S., Tarel, J.-P., and Labayrade, R. (2003). On

the design of a single lane-markings detector regard-

less the on-board camera’s position. pages 564–569,

Colombus, OH, USA. Proceedings of IEEE Intelligent

Vehicle Symposium.

Kim, Z. (2008). Robust lane detection and tracking in chal-

lenging scenarios. IEEE Transactions on Intelligent

Transportation Systems.

Lopez, A., Canero, C., Serrat, J., Saludes, J., Lumbreras, F.,

and Graf, T. (2005). Detection of lane markings based

on ridgeness and ransac. IEEE Conf. on Intelligent

Transportation Systems.

McCall, J. and Trivedi, M. (2006). Video based lane esti-

mation and tracking for driver assistance: Survey, sys-

tem, and evaluation. IEEE Trans. Intell. Transp. Syst.

Wang, Y., T. E. and Shen, D. (2004). Lane detection and

tracking using b-snake. Image and Vision Computing.

Wu, B.-F. and Lin, C.-T. (2007). Robust lane detection and

tracking for driving assistance systems. IEEE Interna-

tional Conference on Systems, Man and Cybernetics.

Zhou, Y., Xu, R., Hu, X., and Ye, Q. (2006). A robust lane

detection and tracking method based on computer vi-

sion. volume 17, pages 736–745. Measurement Sci-

ence and Technology.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

460