UNDERSTANDING OBJECT RELATIONS IN TRAFFIC SCENES

Irina Hensel, Alexander Bachmann, Britta Hummel and Quan Tran

Department of Measurement and Control, Karlsruhe Institute of Technology, 76131 Karlsruhe, Germany

Keywords:

Intelligent vehicles, Object relations, Markov logic.

Abstract:

An autonomous vehicle has to be able to perceive and understand its environment. At perception level objects

are detected and classiﬁed using raw sensory data, while at situation interpretation level high-level object

knowledge, like object relations, is required. In order to make a step towards bridging this gap between low-

level perception and scene understanding we combine computer vision models with the probabilistic logic

formalism Markov logic. The proposed approach allows for joint inference of object relations between all

object pairs observed in a trafﬁc scene, explicitly taking into account the scene context. Experimental results

based on simulated data as well as on automatically segmented trafﬁc videos from an on-board stereo camera

platform are provided.

1 INTRODUCTION

To enable autonomous driving, a vehicle has to per-

ceive and interpret its environment with respect to the

driving task. Perception in this context refers to the

detection and classiﬁcation of objects based on raw

sensory data, whereas interpretation denotes inferring

and manipulating high-level scene descriptions based

on this data, such as relations between objects and

driver intentions. Methods from the ﬁeld of cog-

nitive vision aim at bridging the gap between per-

ception and interpretation, by using abstracted sen-

sor data together with explicitly encoded prior knowl-

edge and inference procedures (Vernon, 2006). This

prior knowledge typically takes the form of frequently

occurring spatial and temporal relations between do-

main objects. A couple of formalisms have been

applied to model and exploit such knowledge, such

as: probability theory (Howarth and Buxton, 2000),

frames (Hotz et al., 2008), description logic (Neu-

mann and M

oller, 2008) (Hummel et al., 2008), Sit-

uation Graph Trees (Arens et al., 2004), Scenarios

(Georis et al., 2006) and lately Markov logic (Tran

and Davis, 2008). Typical applications of such meth-

ods include surveillance tasks, interpretation of aerial

images or analysis of trafﬁc situations. Some related

work that links trafﬁc videos to conceptual relational

knowledge is outlined in the following. (Howarth and

Buxton, 2000) derive conceptual representations of

events from model-based object tracking data com-

puted on trafﬁc videos from a roundabout.

(Cohn et al., 2006) overview a system that can learn

trafﬁc behaviour using qualitative spatial relation-

ships among close objects travelling along learned

paths. Another system, presented in (Gerber and

Nagel, 2008), imports extracted geometrical trajec-

tories from inner-city monocular videos into a con-

ceptual representation of elementary vehicle actions

based on a fuzzy metric-temporal Horn logic. The

same knowledge formalism is used in (Fern

andez

et al., 2008) as a basis for an integrative architecture

of a cognitive vision system, which extracts textual

descriptions of a recorded pedestrian crossing sce-

nario. (Arens et al., 2004) demonstrate that high-level

hypotheses about intended vehicle behaviour can be

used to improve tracking under occlusion. The next

two recent works use Markov logic as a representation

language. That is a novel probabilistic logic formal-

ism, which can handle uncertain and imperfect data

(Richardson and Domingos, 2006). (Tran and Davis,

2008) addresses the task of visual recognition of inter-

actions of people and vehicles at a parking lot. (Bach-

mann and Lulcheva, 2009) classiﬁes multiple inde-

pendently moving objects by taking into account ex-

isting object relations.

With the exception of (Bachmann and Lulcheva,

2009) all publications mentioned use videos recorded

from static cameras. Furthermore, relations between

object pairs are inferred without taking scene context

into account. This can lead to a globally implausible

scene description since it is hard to detect noise and

outliers in the sensor data.

389

Hensel I., Bachmann A., Hummel B. and Tran Q. (2010).

UNDERSTANDING OBJECT RELATIONS IN TRAFFIC SCENES.

In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 389-395

DOI: 10.5220/0002832603890395

 SciTePress

To address these issues, this contribution presents

an approach that allows for joint inference of relations

between all object pairs in a scene, thus explicitly tak-

ing into account the scene context. Moreover, traf-

ﬁc videos are acquired from a stereo camera platform

that is mounted inside a moving vehicle.

The proposed system automatically segments im-

ages into object hypotheses. Motion proﬁle and posi-

tion in space are estimated for every object hypothe-

sis. This quantitative sensor data is mapped onto sym-

bols and an evidence ﬁle is generated. Markov logic

models for understanding object relations in a trafﬁc

scene are developed and trained on a set of trafﬁc im-

ages. The evidence together with the trained model

are provided as input to the Markov Logic reasoner.

As a result conditional probabilities for the validity of

the modelled object relations between every two ob-

jects in the scene are computed.

This paper is organised as follows: next section

will give a short theoretical introduction to Markov

logic. Then the vocabulary used in our trafﬁc scene

models is introduced in form of an ontology. Sec-

tion 4 describes the trafﬁc scene models developed in

Markov logic. Finally, Section 5 provides experimen-

tal results on simulated and real data.

2 MARKOV LOGIC

Markov logic combines ﬁrst-order logic with Markov

random ﬁelds. It provides a framework for explicitly

modeling relations in complex domains, while taking

into account uncertainties and performing probabilis-

tic inference (Richardson and Domingos, 2006). A

Markov logic network (MLN) L consists of a set of

weighted logic formulae (F

, g

) describing a spe-

ciﬁc domain. The formulae F

are constructed from

logical atoms (e.g. sceneObject(o)) linked with log-

ical connectives and quantiﬁers. The attached real

valued weights g

validate the assertions stated over

the domain by the corresponding formulae and can be

learned from training data. Given L and a ﬁnite set of

logical constants B (e.g. O1) all possible groundings

of each logical atom X (e.g. sceneObject(O1)) and

all possible groundings of each formula G can be in-

stantiated by substituting all (typed) variables by con-

stants from B. Each ground formula in G is assigned

the weight of the underlying ﬁrst-order formula from

L. The set of ground atoms X can be seen as a set of

binary random variables and therefore be represented

by an Markov random ﬁelds M(L, B), which has a bi-

nary node for every X

. The value of a node is 1, if

the corresponding ground atom is true and 0 other-

wise. There is an edge between two nodes of M(L, B)

iff the corresponding ground atoms appear together in

at least one element of G. Thus, all ground atoms of

a ground formula constitute a clique in M(L, B). The

state x

{m}

of the m-th clique is evaluated by the fea-

ture f

{m}

) ∈ {0, 1} of the corresponding ground

formula from G and by the weight g

assigned to it.

The value of the feature f

{m}

) is 1, if G

is sat-

isﬁed by x

{m}

, i.e. if the ground formula is true. The

joint distribution of M(L, B) is

P(X = x) = Z

−1

exp



∑

{m}

)



where Z is a normalization factor. Algorithms for

learning and inference in MLNs are implemented in

the open-source package Alchemy (Kok et al., 2007)

and have been used throughout this work.

3 ONTOLOGY

Knowledge about object attributes and object rela-

tions to other scene objects is described using a de-

ﬁned vocabulary. Figure 1 shows the pictorial rep-

resentation of the ontology formalised in ﬁrst-order

logic. The arity of each predicate symbol, that is

the number of its typed logical variables, is shown in

brackets (as e.g. hasSpeed(object,speed)).

isa

sceneObject(1)

cross(2)

follow(2)

distance

speed

Zero

relation

flank(2)

VeryClose

VeryLow

name

difference

Equal

hasDiffIn

Orient(3)

Crossing

Opposite

position

moveTowards(2)

movePast(2)

moveAwayFrom(2)

approachOncoming(2)

flankOncoming(2)

leaveOncoming(2)

approachCrossing(2)

leaveCrossing(2)

hasSpeed

(2)

hasRelPos

(3)

hasDistance

(3)

Figure 1: Object relation ontology. In order to maintain

readability some conceptual values of the object attribute

classes are left out. The numbers in brackets denote the ar-

ity of each predicate symbol.

Object Attributes. The scene object concept is

connected with all modelled object attributes (see

Figure 1). One can distinguish between self object

attributes, which refer to one object, and relative

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

390

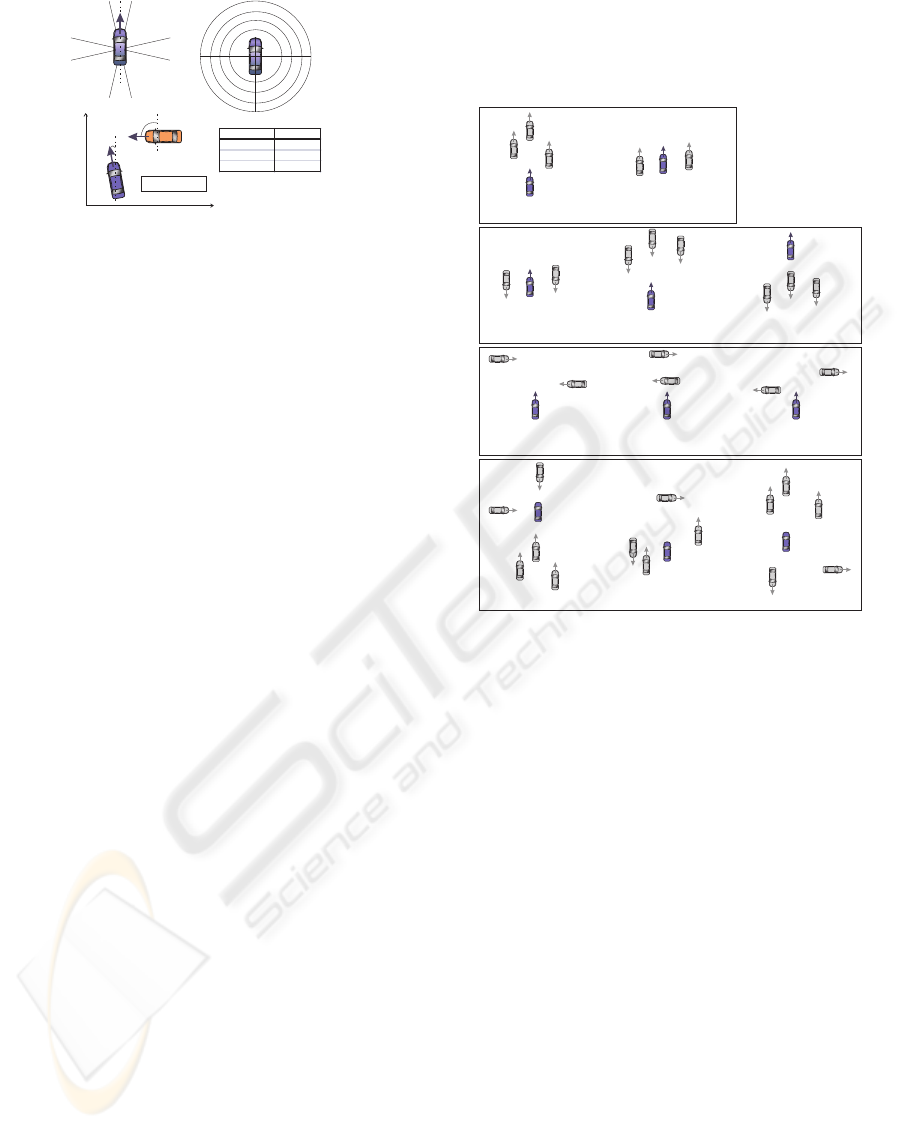
10°

80°

100°

-10°

SW SE

Dy y y=| - |

1 2

|Δψ| [°] difference

0 £ y £ 30 Equal

30 < y £ 150 Crossing

150 < y £ 180 Opposite

(a)

20 70 250[m]

Far

(b)

(c)

Figure 2: Conceptual values for relative position, relative

distance and relative orientation.

object attributes, which refer to two objects. Respec-

tively, there is a predicate symbol of proper arity that

explicates each of these links. The quantitative value

range of every modelled attribute is discretised in a

proper set of conceptual values that are formalised

as logical terms (e.g. VeryLow). The modelled object

attributes are: speed - object speed; difference - dif-

ference in orientation between two objects; position -

relative position between two objects and distance -

relative distance between two objects. All conceptual

values of an object attribute are modelled as pairwise

disjoint and jointly exhaustive (see Figure 2).

Object Relations. An object relation in this work de-

notes an elementary action of a trafﬁc participant sup-

plemented by a reference to another relevant scene

object. All object relations depicted in Figure 1 are

formalised as predicates of arity 2 with both variables

being of type object, as e.g. follow(object,object). Ev-

ery object relation is speciﬁed for the second entry

(primary object) with respect to the ﬁrst one (refer-

ence object), e.g. follow(O1,O2) reads “O2 follows

O1”. The object relations represent general relations

between two moving objects or between a moving and

a standing object. The meaning of each object relation

is visualised in Figure 3.

4 MODEL

This section introduces several trafﬁc scene models

developed in Markov logic. They consist of a number

of ﬁrst-order logic rules formulated with the predi-

cates introduced in the previous section. These rules

can be divided into hard and soft rules. Hard rules are

assumed to be deterministic and obtain a large pos-

itive weight attached without a training phase. Soft

rules make assertions over the domain that are only

typically true. The weights associated with them

are learned from hand-labeled training data generated

from images of urban, rural road and highway trafﬁc

scenes.

Thereby all free logical variables in the examples

below are to be considered as implicitly universally

quantiﬁed.

follow(O2,O1)

flank(O2,O1)

flank(O1,O2)

flankOncoming(O2,O1)

flankOncoming(O1,O2)

approachOncoming(O2,O1)

approachOncoming(O1,O2)

leaveOncoming(O2,O1)

leaveOncoming(O1,O2)

approachCrossing(O2,O1)

approachCrossing(O1,O2)

cross(O2,O1)

cross(O1,O2)

leaveCrossing(O1,O2)

(v=0)

moveTowards(O1,O2)

(v=0)

movePast(O1,O2)

(v=0)

moveAwayFrom(O1,O2)

Figure 3: Exemplary trafﬁc scenes visualising the meaning

of the object relations.

4.1 Object Relations MLN (OR MLN)

Object Relations MLN (OR MLN) models dependen-

cies between the introduced object attributes and ob-

ject relations. In the training phase for this MLN a

formal deﬁnition of object relations in terms of object

attributes is learned.

In OR MLN hard formulae describe the taxonomi-

cal structure of the object attribute predicates and their

properties, such as symmetry or disjointness. The

predicates hasRelDist and hasDiffInOrient describe

symmetric relative object attributes, while hasRelPos

is unsymmetric.

Soft rules model the correspondence between ob-

ject attribute values and object relations. There

are rules that explicit the dependencies between the

movement state of two different objects and the

present object relation, e.g. if both objects are stand-

ing still none of the introduced object relations is

valid, if both objects are moving none of the relations

moveTowards, movePast and moveAwayFrom is valid,

and if one of the objects is moving and the other is

standing, then none of the object relations, represent-

ing occurrences between two moving objects, is valid.

UNDERSTANDING OBJECT RELATIONS IN TRAFFIC SCENES

391

Further, there are a set of rules that link the remain-

ing three modelled object attributes with each of the

object relations, e.g. :

!(o1=o2) ∧ hasRelPos(o1,o2,+p) ⇒ follow(o1,o2)

!(o1=o2) ∧ hasRelDist(o1,o2,+dist) ⇒ follow(o1,o2)

!(o1=o2) ∧ hasDiffInOrient(o1,o2,+d) ⇒ follow(o1,o2)

In the syntax of Markov logic a “!” denotes logical

negation. The plus operator preceding the variables

in the above example makes it possible to learn a sep-

arate weight for each formula obtained by grounding

the variable with every possible conceptual value of

the corresponding object attribute. This can be in-

terpreted as learning a “soft deﬁnition” for every ob-

ject relation. The weights of the soft rules are learnt

using the discriminative training algorithm from the

Alchemy system (Kok et al., 2007).

The full OR MLN consists of the deﬁned hard

rules and the soft rules with learned weights. It softly

deﬁnes the object relations in terms of the object at-

tributes. Figure 3 visualises several examples of these

learned deﬁnitions for each object relation. Symmet-

ric object relations are indicated in the Figure.

4.2 Scene Consistency MLN (SC MLN)

Using OR MLN one can infer the present object rela-

tions between all possible pairs of objects in a trafﬁc

scene given the object attributes. Thereby all object

relations are inferred jointly. However, uncertainties

in the measurement of the object attributes can still

lead to a globally inconsistent scene description. This

is addressed within the Scene Consistency MLN (SC

MLN), which models which object relations may be

valid at once among three scene objects.

SC MLN consists of soft rules constructed with

object relation predicates only. Despite of rules that

state which object relations are symmetrical, there are

a number of rules that describe plausible object rela-

tions between three different scene objects, such as:

!(o0=o1) ∧ !(o0=o2) ∧ !(o1=o2) ∧

follow(o1,o0) ∧ follow(o1,o2) ⇒

follow(o0,o2) ∨ follow(o2,o0) ∨ ﬂank(o2,o0)

All combinations of object relations with three objects

are modelled. Figure 4 shows all constructed rules in

a schematic way. The abbreviations used are listed in

Table 1. All of these formulae are constructed analo-

gously to the one written above. The rows and lines

in Figure 4 contain the predicates from the left side of

the formula and the corresponding matrix entry con-

tains the right side of the formula (the possible plau-

sible object relations for this case). The formula from

above, for example, is build from row one and line

one.

The constructed rules are trained generatively on

hand labeled training data. The weighted knowledge

base forms the SC MLN.

Table 1: Abbreviations of object relation predicates used in

Figure 4.

fo10 follow(o1,o0)

ﬂ10 ﬂank(o1,o0)

aO10 approachOncoming(o1,o0)

fO10 ﬂankOncoming(o1,o0)

lO10 leaveOncoming(o1,o0)

aC10 approachCrossing(o1,o0)

lC10 leaveCrossing(o1,o0)

c10 cross(o1,o0)

mT20 moveTowards(o2,o0)

mP20 movePast(o2,o0)

mA20 moveAwayFrom(o2,o0)

4.3 SCOR MLN

SCOR MLN stands for the combination of the above

presented SC MLN and OR MLN. It consists of all

hard rules and weighted soft rules of both MLNs.

While OR MLN models relations between object

pairs, SC MLN models the plausibility of a scene as a

whole. Thus SCOR MLN allows for a global look at

a trafﬁc scene.

4.4 Evidence/ Inference

The available quantitative information about do-

main objects is mapped onto logical constants us-

ing qualitative abstraction. The constants represent

objects (e.g. O1), conceptual values of self object

attributes (e.g. Zero) or conceptual values of rel-

ative object attributes (e.g. NW). The set of true

ground atoms resulting from the abstracted constants

(sceneObject(O1), hasSpeed(O1,Zero), etc.) is the ev-

idence given as input to the reasoner.

Based on the MLN and evidence, a grounded

Markov network specifying the joint distribution is

constructed and the conditional probability that a par-

ticular ground atom is true, can be inferred (e.g. that

O1 follows O2). This way the probability that a par-

ticular object relation holds can be estimated for every

evidence object pair at every discrete time step.

5 EXPERIMENTS

Experiments were carried out on simulated data as

well as on automatically segmented trafﬁc image se-

quences. In all experiments the MC-SAT Algorithm

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

392

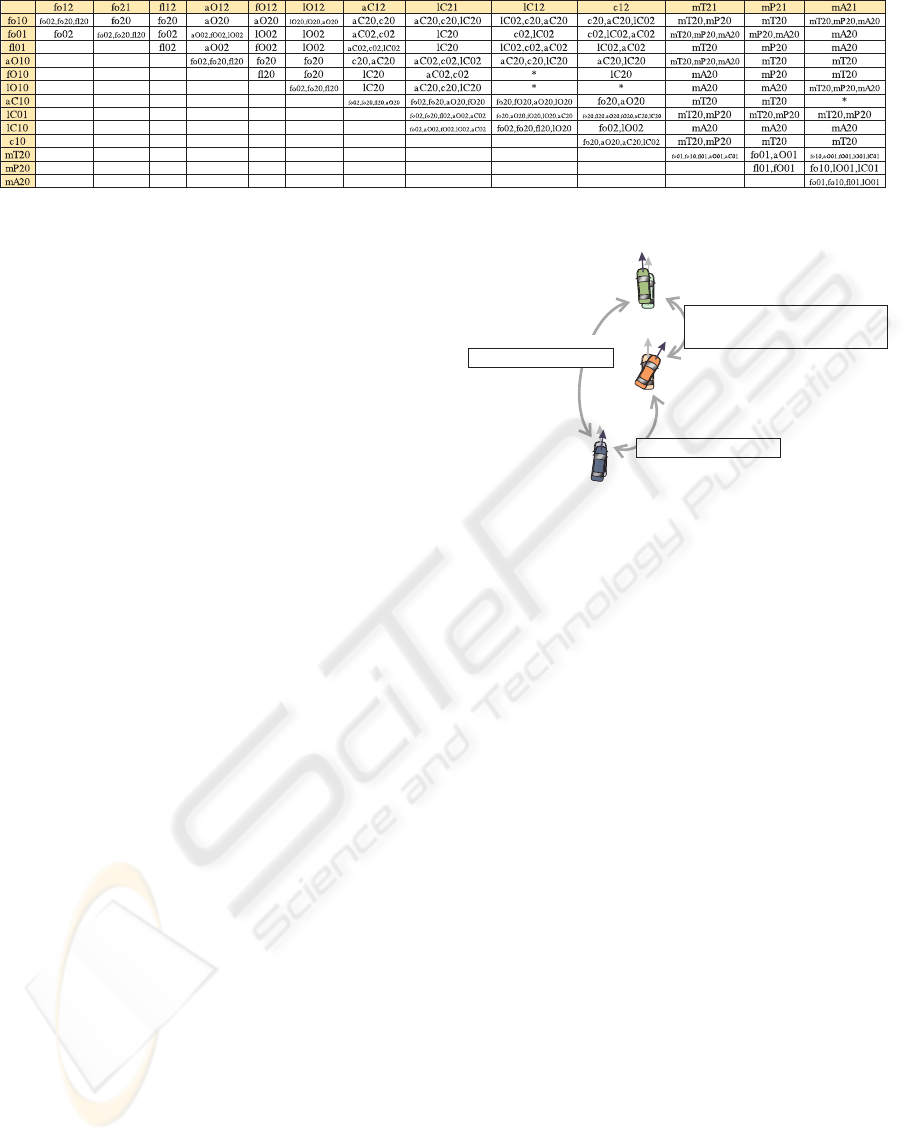
Figure 4: SC MLN formulae encoded in a matrix form. Abbreviations are depicted in Table 1.

from Alchemy was used for inference (Richardson

and Domingos, 2006).

5.1 Simulated Example

The following simulation exempliﬁes the need of a

global view on a trafﬁc scene. A situation with three

cars O0, O1 and O2 is simulated. All three cars are

moving in the same direction, so that for every ob-

ject pair the object relation follow is valid. Mea-

surement uncertainty with respect to object orienta-

tion was added and the resulting scene is shown in

Figure 5. The corresponding abstracted conceptual

values of all modelled object attributes are depicted

in Figure 5 in brackets, while inferred results of OR

MLN and SCOR MLN are shown in boxes. Thereby

only the inferred object relations with highest proba-

bility are listed. Because of the simulated uncertainty

for O0, the conceptual values for the relative object

attribute difference in orientation result in Equal be-

tween O0 and O2 as well as between O1 and O2,

but Crossing between O0 and O1. A contradiction in

these measured attributes is easy to see, if we look

at the scene described by the object attributes as a

whole: if O2 has qualitative the same orientation as

O1 and O0 has crossing orientation to O1, then the

orientation between O0 and O2 should be crossing

too; or, if same orientation between O1 and O2 and

between O0 and O2 holds, then it should hold also

between O0 and O1. The OR MLN is not capable of

resolving this contradiction, since it infers the object

relations considering the object attributes only. The

SCOR MLN, however, takes the consistency of the

scene into account, which leads to a considerable in-

crease in the conditional probability for follow from

0.02 to 0.44.

5.2 Real Data

Video data from an on-board stereo camera platform

are processed with the algorithm described in (Bach-

mann and Dang, 2008) to automatically segment and

track object hypotheses. This method partitions the

image sequence into independently moving regions

{Low,Crossing,NW/S },Close

{Low,Equal,NE/S },Close

{Low,Equal,NE/SW

}

Medium

follow(O1,O0)

leaveCrossing(O0,O1)

approachCrossing(O0,O1)

0,02

0,95

0,35

0,44

0,83

0,05

follow(O1,O2)

0,99 0,98

follow(O0,O2)

0,99 0,99

OR SCOR

SCOR

Figure 5: Simulated trafﬁc scene example with correspond-

ing object attribute values and inference results of OR MLN

and SCOR MLN.

with similar 3-dimensional motion and relative dis-

tance. For every tracked segmented object hypothesis

we obtain a unique identiﬁer. As long as a particu-

lar segmented hypothesis is being tracked, we get for

each frame a bounding box with its dimensions and

height above the estimated ground plane, the charac-

teristic 3D motion of the corresponding region and the

current position in space. These quantitative measure-

ment series are subsequently preprocessed and then

mapped onto conceptual values.

The series preprocessing step is done in batch

mode for a segmented image sequence. At ﬁrst the

measurement series are smoothed. Afterwards ob-

ject speed magnitude and direction for every frame

are calculated from the corresponding 3D motion pro-

ﬁle. Further, relative distance, relative position and

difference of orientation are computed for each pos-

sible pair of moving objects in the frame. Thereby

we consider the ego-vehicle as a scene object, so that

pair relations between the segmented object hypothe-

ses and the ego-vehicle are also evaluated. The dif-

ference in orientation is determined by substracting

the speed direction angles of both objects. By com-

puting the relative position between a reference and a

primary object a reference system centered at the ref-

erence object is used. The reference axis is thereby

the axis in the direction of motion. We compute the

relative position relation exhaustively for every possi-

ble combination of reference and primary object. The

UNDERSTANDING OBJECT RELATIONS IN TRAFFIC SCENES

393

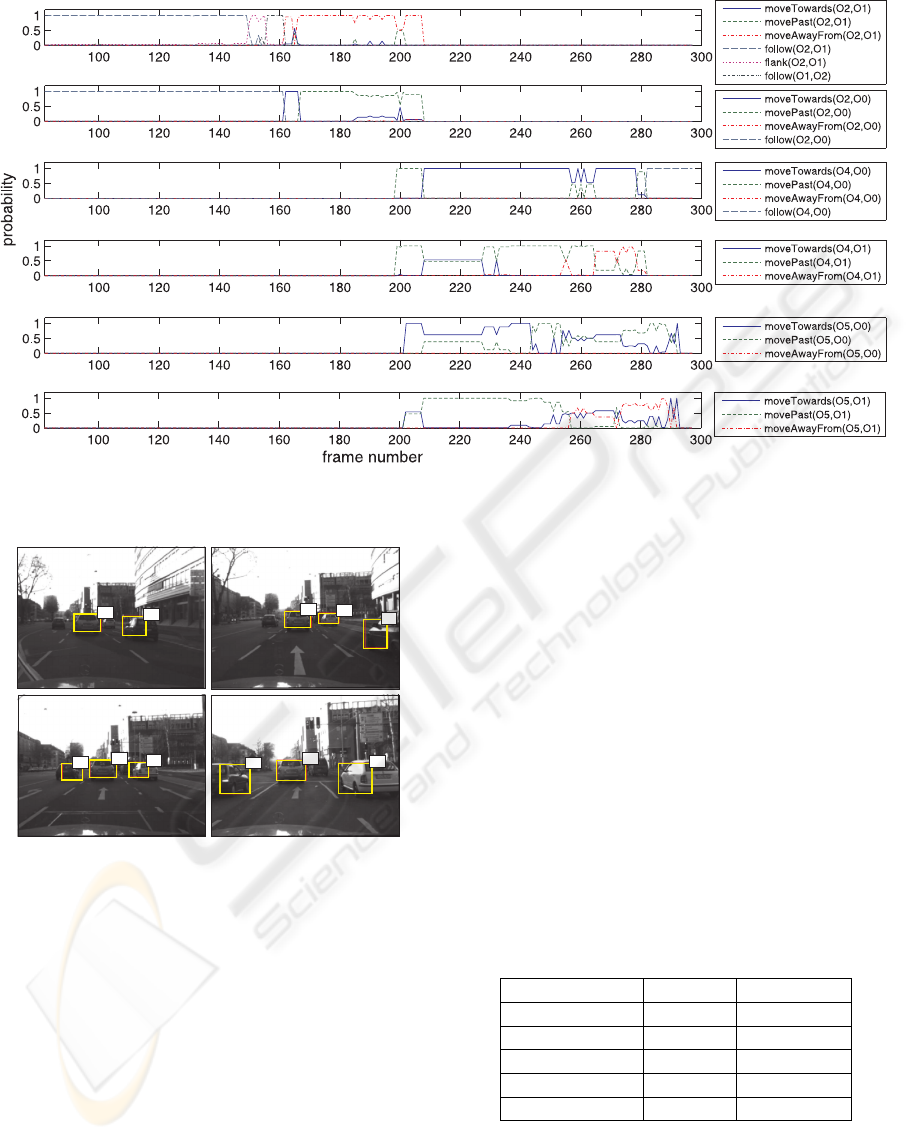
Figure 6: Inference results for selected groundings of the query predicates for all frames of the inner-city test sequence

obtained using SCOR MLN.

frame160 frame200

frame240

frame280

Figure 7: Representative frames from the inner-city test se-

quence with segmented object hypotheses.

calculated quantitative values for all necessary object

attributes and relations are adjacently represented by

conceptual values and abstracted to ground logical

atoms. This abstraction step is carried out for each

frame of the sequence and thus we get as a result one

evidence ﬁle per frame. Inference is run for every

evidence ﬁle generated and so we get inferred proba-

bilities for each frame of the corresponding sequence.

Hence, one should consider the results obtained for

each frame as an individual experiment, which can

be assessed as being acceptable or not. Experiments

on automatically segmented trafﬁc video sequences

are performed with both OR MLN and SCOR MLN.

Thereby query predicates are all modelled object rela-

tions. Exemplary results of SCOR MLN for an inner-

city video sequence are visualised and discussed in

the following. Figure 7 show several characteristic

image frames from the test sequence that reveal the

temporal trafﬁc activities. Object IDs and bounding

boxes of the segmented objects in these images are

depicted too. In Figure 6 the results for all frames of

the test sequence are represented as graphs of inferred

probability versus image frame number for selected

groundings of the query predicates. It can be seen

that the inferred results comply to a great extend with

the sequence ground truth: First, the ego-vehicle O0

follows O1 and O2; then, O2 stops so that O1 and O2

drive by; while O2 disappears from camera sight after

some time, O4 and O5 appear standing still, waiting

at the trafﬁc light; eventually O1 drives between O4

and O5; the ego-vehicle O0 follows O1 throughout

the sequence.

Table 2: AUC ROC results for OR MLN and SCOR MLN.

OR MLN SCOR MLN

follow 0,994051 0,997625

ﬂank 0,574146 0,820281

moveTowards 0,929208 0,919756

movePast 0,900425 0,951633

moveAwayFrom 0,962180 0,978520

In order to gain a quantitative measure for the ac-

curacy of the inferred probabilities, our approach can

be considered as a classiﬁcation task. Therefore, the

area under the receiver operating curve (AUC ROC)

is computed for each object relation seen as a differ-

ent class. Ground truth for the validity of the ob-

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

394

ject relations in every frame from the test sequence

is manually annotated. It should be noted that this

is an ambiguous task depending on the judgement of

the human observer. The AUC ROC results of OR

MLN and SCOR MLN for the test sequence visu-

alised in Figure 7 are listed in Table 2. Hereby the

inferred probabilities of 3384 groundings per mod-

elled object relation were evaluated. The SCOR MLN

achieved signiﬁcantly improved results for most rela-

tions, supporting the claim for considering scene con-

text in complex relational classiﬁcation tasks.

6 CONCLUSIONS

This contribution introduced an approach for inferring

a conceptual representation of relations between ob-

jects in trafﬁc scenes using Markov logic. Soft deﬁni-

tions for object relations in terms of discretised sen-

sor data were learned, as well as typical combinations

of such object relations. These learned models were

tested on automatically segmented trafﬁc videos from

an on-board stereo camera platform. Taking into ac-

count both the soft deﬁnitions and typical scene con-

text, the conditional probability of several object rela-

tions given the learned model and evidence was com-

puted for each object pair in each frame of a test se-

quence. The results complied in most cases with the

judgement of a human observer. The proposed ap-

proach can be seen as a promising step towards bridg-

ing the gap between low-level image processing and

high-level situation interpretation. Future work con-

siders verifying the proposed approach on a broader

statistical base, augmenting the model with temporal

dependencies and closing the loop to low-level scene

segmentation.

ACKNOWLEDGEMENTS

The authors gratefully acknowledge support of this

work by the Deutsche Forschungsgemeinschaft (Ger-

man Research Foundation) within the Transregional

Collaborative Research Centre 28 “Cognitive Auto-

mobiles”.

REFERENCES

Arens, M., Ottlik, A., and Nagel, H. H. (2004). Using be-

havioral knowledge for situated prediction of move-

ments. In KI, pages 141–155. Springer-Verlag.

Bachmann, A. and Dang, T. (2008). Improving motion-

based object detection by incorporating object-

speciﬁc knowledge. International Journal of Intel-

ligent Information and Database Systems (IJIIDS),

2(2):258–276.

Bachmann, A. and Lulcheva, I. (2009). Combining low-

level segmentation with relational classiﬁcation. In

ICCV2009; IEEE Workshop on Visual Surveillance

(VS), pages 1216–1221.

Cohn, A. G., Hogg, D., Bennett, B., Devin, V., Galata, A.,

Magee, D., Needham, C., and Santos, P. (2006). Cog-

nitive vision: Integrating symbolic qualitative repre-

sentations with computer vision. In Christensen, H. I.

and Nagel, H. H., editors, Cognitive Vision Systems:

Sampling the Spectrum of Approaches, volume 3948

of LNCS, pages 221–246. Springer.

Fern

andez, C., Baiget, P., Roca, X., and Gonz

ılez, J.

(2008). Interpretation of complex situations in a

semantic-based surveillance framework. Image Com-

mun., 23(7):554–569.

Georis, B., Mazire, M., Br

emond, F., and Thonnat, M.

(2006). Evaluation and knowledge representation for-

malisms to improve video understanding. In Proceed-

ings of the International Conference on Computer Vi-

sion Systems (ICVS’06), New-York, NY, USA.

Gerber, R. and Nagel, H. H. (2008). Representation of oc-

currences for road vehicle trafﬁc. Artif. Intell., 172(4-

5):351–391.

Hotz, L., Neumann, B., and Terzic, K. (2008). High-level

expectations for low-level image processing. In KI,

pages 87–94. Springer-Verlag.

Howarth, R. J. and Buxton, H. (2000). Conceptual descrip-

tions from monitoring and watching image sequences.

Image Vision Comput., 18(2):105–135.

Hummel, B., Thiemann, W., and Lulcheva, I. (2008). Scene

understanding of urban road intersections with de-

scription logic. In Cohn, A. G., Hogg, D. C., M

oller,

R., and Neumann, B., editors, Logic and Probability

for Scene Interpretation, number 08091 in Dagstuhl

Seminar Proceedings, Dagstuhl, Germany.

Kok, S., Sumner, M., Richardson, M., Singla, P., Poon, H.,

Lowd, D., and Domingos, P. (2007). The Alchemy

system for statistical relational AI. Technical report,

Department of Computer Science and Engineering,

University of Washington, Seattle, WA.

Neumann, B. and M

oller, R. (2008). On scene interpreta-

tion with description logics. Image Vision Comput.,

26(1):82–101.

Richardson, M. and Domingos, P. (2006). Markov logic

networks. Machine Learning, 62(1-2):107–136.

Tran, S. D. and Davis, L. S. (2008). Event modeling and

recognition using markov logic networks. In ECCV

’08: Proceedings of the 10th European Conference on

Computer Vision, pages 610–623, Berlin, Heidelberg.

Springer-Verlag.

Vernon, D. (2006). The space of cognitive vision. In Chris-

tensen, H. I. and Nagel, H. H., editors, Cognitive Vi-

sion Systems: Sampling the Spectrum of Approaches,

volume 3948 of LNCS, pages 7–26. Springer.

UNDERSTANDING OBJECT RELATIONS IN TRAFFIC SCENES

395