NON-PARAMETRIC BAYESIAN ALIGNMENT AND RECOVERY

OF OCCLUDED FACE USING DIRECT COMBINED MODEL

Ching-Ting Tu and Jenn-Jier James Lien

Robotics Laboratory, Department of Computer Science and Information Engineering

National Cheng Kung University, Tainan, Taiwan, R.O.C.

Keywords: Principal Component Analysis (PCA), Eigenface, Statistical Image Models.

Abstract: This paper focuses on the problem of recovering the occluded facial image automatically with the aid of

domain specific prior knowledge and no manual face alignment or user-specified occlusion region is

needed. The robust alignment and occlusion recovery are solved sequentially by a novel recovery scheme

called the direct combined model (DCM). Local occluded facial patches are recovered by utilizing the

information propagated from other non-occluded patches and is further constrained by a global facial

geometry. The error residue between the recovered result and the geometric constraint is then used for

updating the parameter of alignment function for the next iteration. Into this recovering framework, DCM

efficiently and robustly updates the results of recovering and aligning based on a compact statistic model

representing the prior updating knowledge. Our extensive experiment results demonstrate that the recovered

images are quantitatively closer to the ground truth with no manual alignment and occlusion dection.

1 INTRODUCTION

Recently, with the help of a large collection of other

facial images, a number of face occlusion recovery

techniques have been developed. Park et al. (Park et

al., 2005) and Saito et al. (Saito et al., 1999) propose

methods to remove occlusion and reconstruct facial

images with principal component analysis (PCA).

However, the results synthesized via the original

PCA process are highly affected by the appearance

and location of the occlusion. Subsequently, Hwang

et al. (Hwang et al., 2003) and Mo et al. (Mo et al.,

2004) presented methods to recover occluded faces

using two separate eigenspaces sharing the same

coefficients. However, the occluded and non-

occluded appearances have an entirely different

character, recovery results using the same weights

for two different spaces tends to be inaccurate.

Furthermore, the learning-based facial recovery

methods are required automatically detecting the

occluded area and aligning the test image with

training examples. However, pervious methods, e.g.

(Hwang et al., 2003; Lin et al., 2009; Mo et al.,

2004), are need a user either to specify the occlusion

region or to align the occluded face images.

This paper unifies the tasks of automatic occluded

face recovery, detection, and alignment in a

Bayesian framework, and solves these problems

sequentially by a novel particle-based recovery

scheme. In this framework, we introduce a novel

learning algorithm, DCM, to deterministically and

robustly infer the affine parameters and the

recovered facial appearance.

2 DIRECT COMBINED MODEL

The DCM algorithm assumes there are two related

classes: class X and class Y, e.g. the facial

appearances of occluded and non-occluded patches

or the affine parameter and the corresponding facial

appearance. Let the structure of the coupled training

dataset be

11 2 2

(, ),(, ) ,( , )

yxy xy…, , where N is

the total number of

(, )

y feature pairs. The

combined principal space

[]

TTT

for minimizing

the energy function

(,,)

UUW

|| || || ||

iXi iYi

Uw x y Uw y

−−+ −−

∑∑

(1)

can be solved by SVD process, where and w

is the

weight set calculated by projecting each feature pair,

(, )

y , onto the combined principal space

[]

TTT

and

(, )

y is the mean vector pair.

495

Tu C. and James Lien J. (2010).

NON-PARAMETRIC BAYESIAN ALIGNMENT AND RECOVERY OF OCCLUDED FACE USING DIRECT COMBINED MODEL.

In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 495-498

DOI: 10.5220/0002833704950498

 SciTePress

Figure 1: Workflow of testing process consists of (a) geometry/illumination normalization, (b) patch-based occlusion

detection and recovery, (c) probabilistic propagation: (c.1) face-based measurement, (c.2) drift, and (c.3) diffuse.

According to (De la Torre et al., 2001), the

common drawback of such combined formulation,

[]

TTT

, is that it is not suitable for predicating

from one class to another. We exploit the

fundamental property of SVD in Eq.(1), the

unpredictable problem is resolved via a MMSE

criterion.

ˆˆ

() argmin ( ) (, )

yx y y PxydXdY=−

∫∫

(2)

where (, )Pxy is the joint probability of feature

vectors x and y, and

()yx

is the estimated vector y

for a given x. According, it is the expected value or

vector of the posterior probability of y for a given

observation x,

[| ]EY X x= .

Under the assumption that the joint distribution

of X and Y in Eq. (1) is a multivariate normal

density, Eq.(2) further is derived:

(

)

†

()

yx y UU x x=+ −

(3)

where

†

is the right inverse matrix of

that can

be approximated by the SVD algorithm. Eq. (3) is

defined as the DCM transformation from X to Y,

where the regression matrix

†

can be calculated

in off-line. Especially, in contrast to the standard

multiple multivariate linear regression approach, the

DCM transformation extracts only a few significant

feature pairs to represent the relevant information,

and thus, the major features of the X-Y correlation

are better captured.

3 DCM-BASED BAYESIAN

ALIGNMENT AND RECOVERY

We introduce a Bayesian framework to bind the

tasks of occluded facial image alignment and

recovery and the occlusion detection together, and

address such a task by a novel particle-based scheme

to model the posterior probability density function.

The proposed process takes both the global and local

facial appearance components of the input image

into account, and sequentially recovers and

propagates the particles by embedding with the

DCM algorithm.

3.1 Unified Probability Model

Following the sequential recovery algorithm, the

recovered facial appearance f in an image I is

inferred from the previously recovered result

′

arg max ( | , , ) ( , | , )

Pf bIP b f Iddb

ξξ

′

∫∫

(4)

where the affine parameter

and the PCA weight

vector b are included for aligning f with training

examples and for guaranteeing the global facial

geometric structure of f. It naturally decomposes into

two terms:

Posterior Probability

(|,,)Pf bI

. Since the

weight vector b is independent from the affine

parameter

, the posterior density term are factored

as (| )( |,)Pb f P f I

in the recovery stage (sec

3.2).

Propagation Probability

(, | ,)

bfI

′

. It is

defined as the probabilistic propagation formulation:

(, | ) (, | , ) ( , | )

pbf Pb bP bfddb

ξξξξξ

′′

′

′′ ′′ ′ ′ ′

∫∫

(5)

where

and

are from the previous iteration.

Fig. 1 illustrates the proposed particle based

solution for this Bayesian framework. In practice,

particles

are sampled based on two inner corner

(a) Geometry/Illumination

Normalization

(b) Local Patch-based Occlusion Detection and

Recovery

[,]

[]

[,]

(c.1) Global Face-based Measurement

(c.2) Drift

(c.3) Diffuse

P+



{( )}

iii

PP P

=+Δ

{,()}

iiii



O-De

O-Re

{()}

iii

Pr+Re

{,()}

()

iiii

−

∝Δ = −

{}

{' }

ii ii

PPP

=+Δ

{''}

ii ii

PP P

=+Δ

{}

{' '}

iii

+Δ

-S: Sampling

-RS: Re-sampling

-A

: Geometry

Normalization

-A

: Illumination

Normalization

-O-De: Occlusion

Detection

-O-Re: Occlusion

Recovery

-Pr: Projection

on to U

-Re: Reconstruction

based on U

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

496

Figure 2: Training process consists of face-based PCA

creation, patch-based DCM creation, and facial

appearance error-to-eyes position updating DCM creation.

points of the eyes P by an affine transformation

function

via a parameter

. The initial position

of two inner corner points of the eyes

(it is

probably occluded) is roughly detected, and K

initializations particles are randomly generated

around

{}

PP P=+Δ

. The particle weight

measured with its coincidence with the learned

eigenspace

(Initial weights of all particles are

equal). Further, to suppress the effects of

illumination differences between different facial

appearances, a illumination

normalization scheme A

is performed.

3.2 Local-based Occlusion Recovery

The posterior density, (|,,)Pf bI

for recovery

stage is modeled by a Markov network embedded

with the proposed DCM algorithm. Different from

the common patch-based Markov network

approaches (Freeman et al., 2000; Liu et al., 2001;

Sudderth et al., 2003) that selects the recovered

patches from the training database, the current

approach recovers patches by other non-occluded

patches via the DCM transformation.

Learning Patch Pair l-to-m DCM

[]

TTT

(Fig. 2). For each patch

, {1, 2,..., }lm M∈ (each f is

composed of M patches), the l-m patch pairs of N

training facial appearances

{()}

P are used to train

the combined principal space

[]

TTT

and the

DCM transformation from l to m by Eq. (1) and Eq.

(3), respectively.

Occlusion Detection (Fig. 1.b). The confidence of

visibility of patch l is written as c

which is directly

proportional to the difference between the original

local texture detail of patch l and the reconstructed

texture by the bidirectional DCM transforms from l

to m and from m back to l, where the patch m is one

of neighbor patches of l.

Occlusion Recovery (Fig. 1.b). We solve the

defined Markov network by the nonparametric belief

propagation method (NBP) (Sudderth et al., 2003),

but the recovery order is from non-occluded patches

to the occluded patches sorted based on their

confident values, i.e. the c-value.

3.3 Global-based Face Alignment

After the recovery, the higher-weighted particles are

chosen to form the distribution of

(, | )

′′ ′

the face-based measurement step of the probabilistic

propagation stage (Fig. 1.c.1), where only these

correctly aligned ones will be treated as the updating

initializations in the following steps of re-

randomization. According, the summarization of the

current recovered results,

{(), }fP

′

, is the mean of

these particles,

[]

Ef f

∑

Learning the Position-facial Appearance DCM

[]

TTT

ΔΔ

(Fig. 2). Each training image I generates

N’ perturbed facial appearances, {( )}

PP+Δ , by

disturbing elements of the manually labeled position

P. Subsequently,

'NP

Δ of N training images and

their corresponding facial appearance difference

generated by

are used to train the DCM

combined principal space

[]

TTT

ΔΔ

and the DCM

transformation from

PΔ

, respectively.

Face Alignment. The drift step (Fig. 1.c.2) updates

positions

{}PP P

′

+Δ from the given facial

differences,{}

based on the combined space

[]

TTT

ΔΔ

in order to form the transition

probability,

(, | , )

′

. Finally, a diffuse step

(Fig. 1.c.3) is done on these higher-weighted

particles to generate several copies and shift them to

the neighbors of the updated position,

{}

′′

+Δ

The new set of particles then forms the distribution

(, | )

′

for the following step.

4 EXPERIMENTAL RESULTS

The performance of the proposed recovery system

was evaluated by performing a series of

experimental trials using training and testing

databases comprising 100 and 50 facial images,

respectively, where specific facial feature regions of



(, ) {1, , }lm M∀∈…

M×

Local Patch-based

DCM Creation :

DCM:

[]

TTT

Δ= −

: Geometric normalization

: Illumination normalization

S: Samp ling of P

Pr: Projection to eigenspace

Re: Reconstruction based on eigenspace

: Sep arate as M local p atches

{}

iii

{()}

iii

m-patch

ii jji

IPP

++Δ

{{ ( )} }

ii jji

+Δ

N×

{{ ( )} }

ii jji

FP P

+Δ

'NN

[]

TTT

ΔΔ

Facial Appearance and Eye

Position DCM Creation :

DCM:

Global Face-based

PCA Creation:

Eigenspcae:

[]

l-patch

Pr+

()m

()l

NON-PARAMETRIC BAYESIAN ALIGNMENT AND RECOVERY OF OCCLUDED FACE USING DIRECT

COMBINED MODEL

497

the testing images are occluded manually. The

normalized images are 28x96 pixels and the patch

size and overlap size are 13 and 5, respectively.

Fig. 3 presents representative examples of the

reconstruction results. Table 1 presents the average

recovery and alignment errors computed over all the

images in the testing database. Fig. 4 compares the

recovery results obtained using the proposed DCM

method with those obtained by methods in (Hwang

et al., 2003 and in Park et al., 2005).

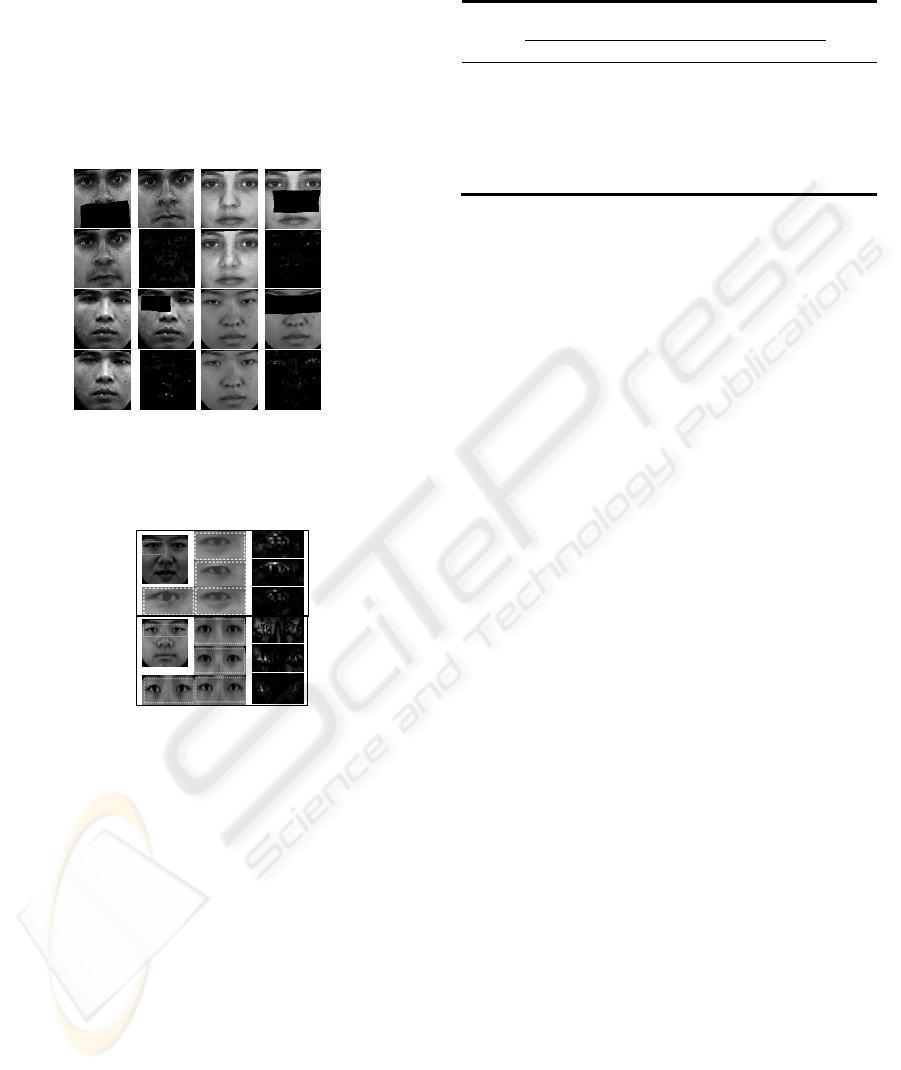
Figure 3: Reconstruction results of the DCM schemes: (1

and 3

rows) occluded and ground truth facial images and

(2nd and 4

rows) reconstructed facial images and its

difference from its ground truth.

Figure 4: Two examples of reconstruction results and

errors using three eigen-based method. (1st column):

original occluded images and the occlude features.

5 CONCLUSIONS

This study has presented a Bayesian framework for

sequential facial occlusion alignment, detection, and

recovery through a DCM-based algorithm. By

considering both local and global facial structures,

our recovered results closely resemble the ground

truth facial appearances. Overall, the proposed

method is a promising way to improve the

performance of existing automatic face recognition,

facial expression recognition, and facial pose

estimation applications.

Table 1: Average and standard deviation of the position P

and the recovered f estimation errors for all images in

testing database by different levels of occlusion.

Facial

features

Ave. Error

(Pixel/Grayvalues)

Std. Dev.

(Pixel/Grayvalues)

Occl

usion

Area

P f P f

Left Eye 0.7 6.6 0.5 1.7 10%

Right

Eye

0.6 6.5 0.6 1.8 10%

Both

Eye

0.7 6.6 0.6 16 24%

Nose 1.0 7.0 1.2 2.0 16%

Mouth 1.6 6.8 1.5 1.9 20%

REFERENCES

De la Torre, F. D.and Black, M. J. (2001). Dynamic

Coupled Component Analysis. CVPR.

Freeman, W.T., Pasztor, E.C., and Carmichael, O.T.

(2000). Learning Low-Level Vision. IJCV, 40: 25-47.

Hwang, B.W. and Lee, S.W. (2003). Reconstruction of

Partially Damaged Face Images Based on a Morphable

Face Model. IEEE Trans. on PAMI, 25: 365-372.

Lin, D. and Tang, X. (2009). Quality-Driven Face

Occlusion Detection and Recovery. ICCV.

Liu, C., Shum, H.Y., and Zhang, C.S. (2001). A Two-Step

Approach to Hallucinating Faces: Global Parametric

Model and Local Nonparametric Model. CVPR.

Mo, Z., Lewis, J.P., and Neumann, U. (2004). Face

Inpainting with Local Linear Representations. BMVC.

Park, J.S., Oh, Y.H., Ahn, S.C., and Lee, S.W. (2005).

Glasses Removal from Facial Image Using Recursive

PCA Reconstruction. IEEE Trans. on PAMI, 27: 805-

811.

Saito, Y., Kenmochi, Y., and Kotani, K. (1999).

Estimation of Eyeglassless Facial Images Using

Principal Component Analysis. ICIP.

Sudderth, E., Ihler, A., Freeman, W., and Willsky, A.

(2003). Nonparametric Belief Propagation. ICCV.

Hwang,2003

‐Park,2005



‐DCM



‐Hwang,2003

‐Park,2005



‐DCM



VISAPP 2010 - International Conference on Computer Vision Theory and Applications

498