TOWARDS REAL-TIME NEURONAL DISPARITY MAP

ESTIMATION

Nadia Baha and Slimane Larabi

Computer Science Department USTHB University, BP 32 EL ALIA, Algiers, Algeria

Keywords:

Disparity map, Neural network, DSI (Disparity Space Image), FPGA.

Abstract:

We propose in this paper a new approach for fast disparity map estimation from pair of stereo images. The

disparity map computing is divided into two main steps. The ﬁrst one deals with computing the initial dispar-

ity map using a neuronal DSI (Disparity Space Image) method. Whereas, the second one is a simple and fast

method to reﬁne the initial disparity map. New strategies and improvements are introduced so an accurate and

fast result can be acquired. In order to reduce the computing time, we implemented some steps of the pro-

posed algorithm on FPGA. Experimental results on real data sets were conducted for evaluating the solutions

proposed and comparative evaluation of our method with two others methods is presented.

1 INTRODUCTION

A great number of approaches for disparity map es-

timation have been proposed in the literature, includ-

ing features-based (Di Stefano et al, 2004; Maas et

al, 1999), area-based (Kumar and Chatterji, 2002;

Ogale and Aloimonos, 2005), DSI-based (Binaghi

et al, 2006; Bobik and Intille, 1999) and energy-

based approaches (Alvarez et al, 2002; Miled and Pes-

quet, 2006). A survey for the different approaches

can be found in (Nalpantidis et al, 2008; Scharstein

and Szeliski, 2002). Area-based techniques utilize

the correlation between the intensity patterns in the

neighborhood of a pixel in the left image and those in

the neighborhood of a corresponding pixel at the right

image. One of the principal factors inﬂuencing suc-

cess of area-based methods is the suitable selection of

window shape and size. Feature-based techniques, in-

stead, stem from human vision studies and are based

on matching segments or edges between two images,

thus resulting in a sparse output. Of course, there

are many other methods that are not strictly included

in either of these two broad classes. The energy-

based approaches are time consuming but very accu-

rate. While these techniques achieve satisfactory re-

sults in certain situations, they are often implemented

using numerical schemes which may be computation-

ally intensive. In this paper, we propose a new ap-

proach for computing a dense disparity map based on

the Artiﬁcial Neural Networks and the DSI data struc-

ture. Our approach divides the matching process into

two steps: initial matching and reﬁnement of dispar-

ity map. Initial disparity map is ﬁrst approximated by

neuronal-DSI method so called (Neural-DSI). Then a

reﬁnement method is applied to the initial disparity

so an accurate result can be acquired. In addition, in

order to accomplish real-time operation, we have im-

plemented some steps of the disparity map calculat-

ing on algorithm on a ﬁeld programmable gate array

FPGA. This paper is organized as follows: section 2

presents the stages followed to compute the initial dis-

parity map. Section 3 presents the reﬁnement method.

In section 4, experiments on real image and an anal-

ysis of the results are presented. Finally, section 5

concludes the paper with some remarks.

2 NEURAL-DSI NETWORK

DISPARITY MAP ESTIMATION

Our approach for disparity map estimation described

in this section is based on the DSI data structure and

the use of a neural network. A new strategy is deﬁned

to reduce the computation time of disparity map.

2.1 Points of Interest Extraction and

Matching

Some points of interest are extracted in the image

and their attributes (gradients and orientations) are

computed. These points are selected depending on

355

Baha N. and Larabi S. (2010).

TOWARDS REAL-TIME NEURONAL DISPARITY MAP ESTIMATION.

In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 355-360

DOI: 10.5220/0002833803550360

 SciTePress

Figure 1: The windows used in DSI Computation.

their high values of intensity, gradient and orientation.

Matching of these points is done using the normalized

correlation (ZNCC) considering the left image to the

right image and vice versa. A valid match is consid-

ered only for those points that yield the best correla-

tion score (Baha and Larabi, 2008). These matched

points will be used in the training of the neural net-

work.

2.1.1 DSI Computation

DSI is an explicit representation of the matching

space introduced by A. Bobik and S. Intille (Bobik

and Intille, 1999). It plays an essential role in the de-

velopment of the overall matching algorithm which

makes use of occlusion constraints.

Assuming that the images pair are rectiﬁed, the

disparity computation concerns thus two matched

points which have the same abscise. For each pixel

, y

) in the left image, the disparity computation

will concerns all pixels of a window W

centered on

. At each pixel p

, y

) of the W

, the matched pixel

, y

) will appertains to the window W

of the

right image centered on p

, y

) (see ﬁgure 1). The

position of W

depends on the disparity d of the pair

, p

) which varies from zero to d

max

, where d

max

represent the highest disparity value of the stereo-

scopic images. The relations which bind two matched

points p

, p

of W

and W

are:

= x

+s ∗ d , y

= y

, where s = ±1 is a sign chosen

so that disparities are always positive.

To determine the disparity of a given pixel

, y

), we calculate for assumed disparity d the

score DSI

) of all p

of the windows W

. The size

of the window was experimentally chosen to be 7× 7.

In the literature, this score is based only on the pixel

intensities. We introduce in this work two additional

features: the gradient and orientation of pixels. The

DSI

) score is then computed for a given disparity

d as the sum of squared difference of three attributes

(intensity, gradient magnitude and orientation) as fol-

low:

DSI

) = (I

, y

) − I

− d, y

))

(1)

DSI

) = (G

, y

) − G

− d, y

))

(2)

DSI

) = (O

, y

) − O

− d, y

))

(3)

Where (I

, I

), (G

, G

), (O

, O

) are respectively

the intensities, gradient magnitudes, orientations val-

ues of the pixels on the left and right images.

DSI

) = DSI

) + DSI

) (4)

To calculate the primary disparity map, This pro-

cess is repeated for each value of the disparity d and

the disparity with the minimal cost DSI

) among

the various costs of neighboring pixels p

of the win-

dow W

in the interval [0, dmax ] will be chosen as

the initial disparity of the pixel p

and will be noted

∗

As the implementation of this method for DSI

computation is time consuming, we propose in the

next section a neural network architecture in order to

parallelize the calculation of various costs and back

propagation of errors.

2.2 Neural Network Architecture

The proposed neural networks is composed by four-

layer network (see ﬁgure 2). The input layer has 147

neurons (3 × 49) of respectively intensities, gradient

magnitudes and orientations of W

pixels. The second

layer has the function to compute the scores DSI

intensities, DSI

of gradient magnitudes and DSI

orientations for each one pixel of the window W

. We

obtain then for each value of the disparity d three (7 ×

7) matrices of scores (d = 0..d

max

To compute the ﬁnal DSI

, the third layer adds

the three correlation scores for each one pixel of the

window (see equation 4). We obtain d

max

+ 1 ma-

trices of 7 × 7 scores. In the fourth layer, for each

value of d, all scores of the W

pixels are added and

constitutes the score SumDSI

of the central pixel.

Then, to the central pixel of the window is asso-

ciated a vector of costs (Aggregation cost) AC =

(SumDSI

, SumDSI

, ..., SumDSI

max

). The minimum

cost amount of the d

max

+1 costs is chosen as the best

score and deﬁnes the disparity d

∗

of the central pixel

of the window.

The neural correlation network must be trained

with the learning procedure before computing the

minimum of SumDSI

values(best score) for each

pixel. To prepare the training data, 150 unmatched

pixels and 50 matched pixels are selected to train of-

ﬂine the network. During training, the differences of

intensities, gradient magnitudes and orientations be-

tween two local windows (one for the left image, the

other for the right) are fed to the network. After the

training, the network should have the ability to differ-

entiate the matched pairs from unmatched ones.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

356

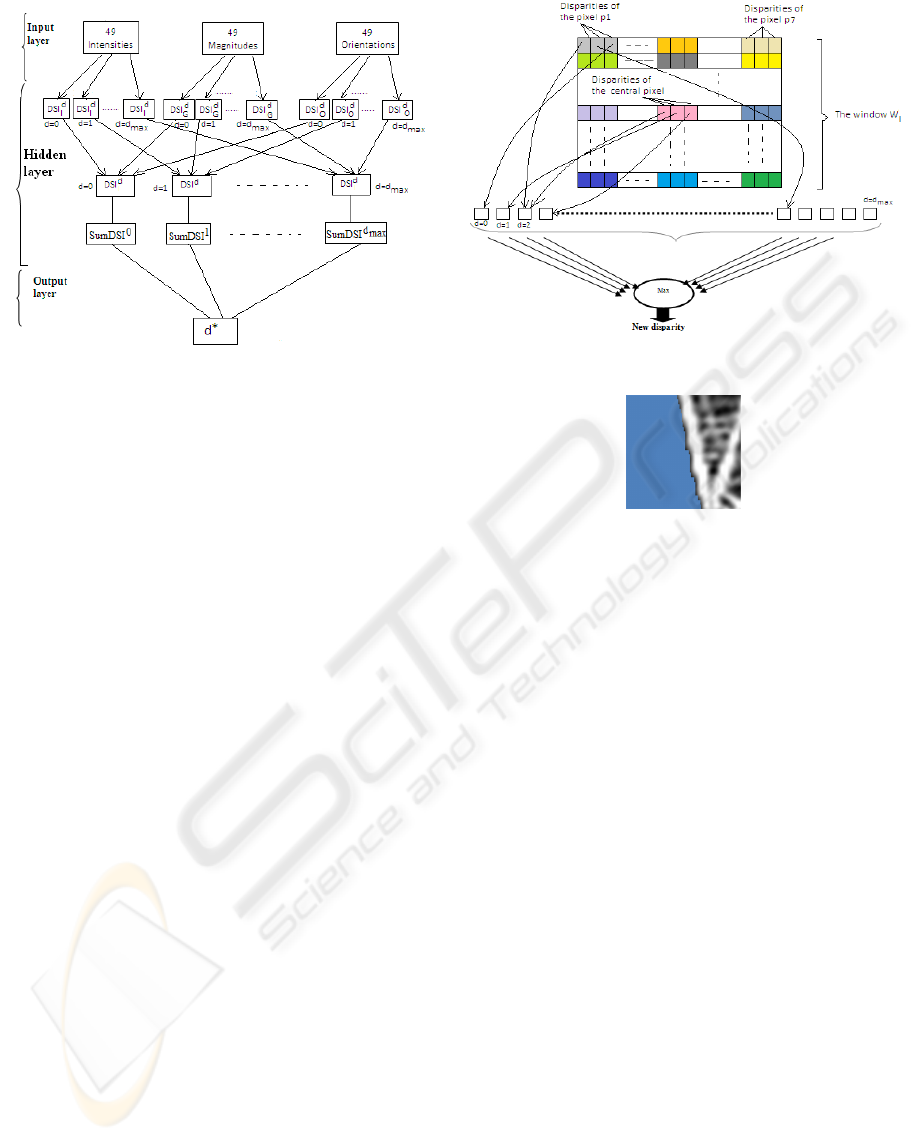
Figure 2: The Neural-DSI network architecture.

3 DISPARITY MAP

REFINEMENT

In this paper we propose the disparity map reﬁnement

by the improvement of Growing Aggregation (GA)

method (Binaghi et al, 2006) and the median ﬁlter ap-

plication.

3.1 Improved Growing Aggregation

Unlike conventional techniques that base further steps

of matching algorithm on the minimal aggregated cost

computed, Binaghi bases decisions on the use of all

scores obtained (Binaghi et al, 2006). Instead to se-

lect in the window W

only one disparity having the

best score, Binaghi propose to select for each pixel n

disparities corresponding to the best scores DSI

We assume that initial disparities of all pixels of

the left image are computed. For each pixel p

the left image, we verify in the ﬁrst if the disparity

is dominant in the window W

. If it is the case, this

disparity will be considered as the ﬁnal disparity and

not necessitates any reﬁnement. Otherwise, we pro-

pose a reﬁnement which consist to select in W

win-

dow three best scores of SumDSI

for each pixel (see

ﬁgure 3). We obtain then the best three disparities as-

sociated to the pixel P

instead of one disparity. The

proposed process consist to apply a vote in order to

choose the dominant disparity in the associated W

us-

ing the three disparities of the central pixel p

and its

48 neighboring pixels.

The disadvantage of all known methods published

is that not address the problem of region bound-

aries(see ﬁgure 4). For this we propose a second im-

provement of GA method by adding a criterion which

Figure 3: Disparity computing with Improved GA.

Figure 4: Example of inter-region problem.

eliminates from the vote process described above all

pixels of the window W

for which the gradient mag-

nitudes have high values relatively to others of the

same window. In this case, only a single disparity

by pixel is considered. Finally, a median ﬁlter is used

for smoothing the disparity map.

4 EXPERIMENTS RESULTS

In this section, we describe the experiments con-

ducted to evaluate the performance of the proposed

method. To this purpose, we examine the main algo-

rithms (DSI, Neural network, improved GA and Me-

dian ﬁlter). Many applications require not only ac-

curate disparities, but also fast runtime (Nalpantidis

et al, 2008). In our case, we will use the computed

disparity map as input for obstacle detection system.

4.1 Initial Disparity Map Results

To compare the result of initial disparity map with

our method (Neural-DSI), two other approaches were

implemented: The neuronal method and DSI method

as described in (Bobik and Intille, 1999), (Binaghi et

al, 2006). We applied these methods on ﬁve images

(Cones, Teddy, Barn1, Sawtooth, Tsukuba) of stan-

dard data sets available on the Middlebury website.

Figures 5 and 6 illustrate the results of initial dis-

TOWARDS REAL-TIME NEURONAL DISPARITY MAP ESTIMATION

357

Figure 5: Initial disparity map obtained with 3 selected

methods.

Figure 6: Processing Time (seconds) of selected algorithms

on the ﬁve image pairs.

parity map obtained for 3 selected methods and the

correspondent processing time (second). This time

depends mainly on the image size. The timing tests

were performed on a PC with a microprocessor of 32

bits, 2.5 GHZ. We can clearly see that, the Neural-DSI

method is fastest relatively to DSI and neural meth-

ods.

4.2 Reﬁnement Disparity Map Results

We implemented our method for disparity map reﬁne-

ment(improved GA + median ﬁlter) so as the neural

reﬁnement method. The obtained results are illus-

trated by ﬁgure 7 and show that our reﬁnement gives

a better map than the neural reﬁnement method.

Figure 8 shows the processing time obtained by

our method (improved GA + median ﬁlter) and the

neural reﬁnement method applied on the ﬁve image

pairs. Also, the proposed reﬁnement is fastest com-

pared to neural reﬁnement method.

We studied also the inﬂuence of window size on

the accuracy of the proposed method. Figure 9 shows

the disparity map obtained after applying our reﬁne-

ment method (improved GA) for the Barn1 image pair

Figure 7: Reﬁnement disparity map obtained with two se-

lected methods.

Figure 8: Processing time (seconds) of the two methods.

for different sizes of the window. More the size of the

window W

is great, more the computed map dispar-

ity is good. Nerveless, the computation time is also

very high when the size of W

became large. Figure

10 illustrates the variation of time processing for three

methods DSI, Neural and Neural-DSI.

Figure 9: Application of Improved GA method on Barn1

image with different window sizes.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

358

Figure 10: Processing time(s) of the selected methods with

different windows size.

Figure 11: Processing time(s) of disparity map computing

of Neural-DSI with different values of d

max

on four images

pairs with 1x7 window.

Experiments are conducted in order to study the

inﬂuence of d

max

values on the performance of the Im-

proved GA method. We used different values of this

parameter for map disparity estimation of four stereo

images pairs with 1x7 window. Figure 11 illustrates

the processing times and show that the Neural-DS I

method is fastest. Indeed, the processing time ob-

tained is less than 0.2seconds.

The results obtained by our algorithm are better

than some methods reported in (Nalpantidis et al,

2008). Indeed the results obtained by (Binaghi et

al, 2004) are satisfactory but not suitable for real-

time applications because the running time needed for

standard image sets is very high. In another method

reported in (Ogale and Aloimonos, 2005), the execu-

tion time varies from 1 to 5 seconds for the standard

image sets . For the window-based method presented

in (Yoon and Kweon, 2006), the running time for the

Tsukuba image pair with 35x35 pixels support win-

dow is about one minute. In the method based on

the Bayesian estimation theory described in (Gutier-

rez and Marroquin, 2004), the results are encouraging

in terms of accuracy but are not suitable for real time

applications, since it takes few minutes to process a

256x255 stereo pair. Another method developed in

(Veksler, 2003), the running times obtained for the

Tsukuba pair is about 6 seconds and 13 seconds for

the Sawtooth pair.

4.3 FPGA Implementation

In order to reduce the computing time, the idea is to

implement certain steps in calculating of the disparity

map on algorithm on a ﬁeld programmable gate array:

FPGA, the processing time can be further reduced.

Indeed the power of FPGAs has attracted researchers

in computer vision. The use of FPGAs is now the

most convenient and reasonable choice for hardware

development. They are cheap and perform extremely

well (Nalpantidis et al, 2008). Based on the previ-

ous study on the calculation of the disparity map, we

can effectively implement some parts of the methods

that are time consuming using FPGAs circuits of Vir-

tex II. The main objective of this work is the design

of various circuits FPGAs for some algorithm previ-

ously presented using hardware description language

VHDL. For this, we have proposed optimal architec-

tures for:

• The Sobel operator: used to calculate the image

gradient

• Neural-DSI: used for the initial disparity map

• Neural Method: used for the reﬁnement

• The Median Filter: used for the reﬁnement

Due to space limitations in this paper, we present

only the processing time obtained for each compo-

nent. To demonstrate the importance of the use of

FPGA circuits, table 1 illustrates the processing time

obtained for each component in traditional implemen-

tation (Soft) where:

- Pair1, Pair2, pair3 are respectively Barn1(432x381),

Teddy(450x375), Tsukuba(384x288)

- Methods 1, 2, 3, 4 correspond respectively to Gradi-

ent (Sobel), Neural DSI, Neural reﬁnement and Me-

dian Filter.

Table 2 illustrates the processing time obtained for

each component using FPGA implementation. Not

surprisingly the running times obtained with the use

the FPGA are better. All the reasons make FPGA im-

plementation preferable.

Table 1: Processing time (ms) for software implementation.

Method 1 2 3 4

Pair1 147 4.32 × 10

31.09 × 10

468

Pair2 163 4.81 × 10

31.92 × 10

470

Pair3 107 3.01 × 10

23.06 × 10

312.5

Table 2: Processing time (ms) for FPGA implementation.

Method 1 2 3 4

Pair1 2.99 14.991 81.90 3.46

Pair2 3.07 15.369 83.99 3.55

Pair3 2.01 10.072 54.78 2.32

TOWARDS REAL-TIME NEURONAL DISPARITY MAP ESTIMATION

359

5 CONCLUSIONS

The disparity map estimation remains an active area

for research in computer vision. More and more mod-

ern applications demand not only accuracy but real-

time operation as well. In this paper, we presented a

disparity map estimation algorithm based on the neu-

ral network and DSI data structure. The disparity map

computing process is divided on to two main steps.

The ﬁrst one deals with computing the initial dispar-

ity map using a neuronal method and DSI structure.

The second one presents our contribution to reﬁne the

initial disparity map using improved GA and median

ﬁlter so an accurate result can be achieved. Experi-

ments results show that the computation time mainly

depends on the image size, window size and the value

of highest disparity in the image. When we imple-

ment some algorithms on FPGA, the processing time

has decreased considerably.

REFERENCES

Alvarez, L., Deriche, R., Sanchez, J., Weickert, J., (2002).

Dense disparity map estimation respecting image dis-

continuities: a PDE and scalespace based approach..

J. of Visual Commun. Image Represent 13, 3-21.

Baha, N., Larabi, S., (2008). Obstacle Detection from Un-

calibrated Cameras. In Proc of PCI’2008, Greece, pp.

152-157.

Binaghi,, E., Gallo,I., Fornasier, C., Raspanti, M., (2006).

Growing aggregation algorithm for dense two-frame

stereo correspondence. In 1st Int.Conf. on Computer

Vision Theory and Application, 326-332.

Binaghi,, E., Gallo,I., Fornasier, C., Raspanti, M., (2004).

Neural adaptative stereo matching. Pattern Recogni-

tion Letters25,1743-1758.

Bobik,A., Intille,S., (1999). Large occlusion stereo. Intern.

Journal on computer vision 33, 181-200.

Di Stefano, L., Marchionni, M., Mattoccia,S., (2004). A

fast area-based stereo matching algorithm. Image and

vision computing, 22(12), 983-1005.

Goulermas,J., Liatsis,P., (2001). Hybrid symbiotic genetic

optimisation for robust edge-based stereo correspon-

dence. Pattern Recognition. 34, 2477-2496.

Gutierrez, S., Marroquin,J., (2004). Robust approach for

disparity estimation in stereo vision. Image and Vision

Computing, 83-195.

Kumar, S., Chatterji, B., (2002). Stereo matching algo-

rithms based on fuzzy approach. Int. Journal in Pattern

Recognit. Artif. Intell. 16,7, 883-899.

Maas, R.,Haar Romeny, B., Viergever, M., (1999). Area-

based computation of stereo disparity with model

based window size selection. Computer Vision and

Pattern Recognition (CVPR), 106-112.

Miled, W.and Pesquet, J., (2006). Dense Disparity esti-

mation from stereo images. Int. Symposium on Im-

age/Video Communication.

Nalpantidis, L., Sirakoulis, G.,and Gasteratos, A., (2008).

Review of stereo vision algorithms: from Software to

Hardware. International Journal of Optomechatron-

ics, 2:435-462, 2008

Ogale, A., Aloimonos, Y., (2005). Shape and the stereo

Correspondence Problem. Int. Journal of Computer

Vision, 65,3,147-1758.

Scharstein, D., Szeliski,R., (2002). A taxonomy and evalu-

ation of dense two-frame stereo correspondence algo-

rithms. Int. Journal on Computer Vision, 47,7-42.

Veksler, O., (2003). Extracting dense features for visual

correspondence with graph cuts. Proc. Of the IEEE

Computer Society Conference on Computer Vision

and pattern Recognition.

Yoon,K., Kweon,I., (2006). Adaptive Support Weight Ap-

proach for Correspondence Search. IEEE Tran. On

Pattern Analysis and Machine Intelligence, vol. 28.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

360