DECOMPOSITION OF A 3D TRIANGULAR MESH INTO

QUADRANGULATED PATCHES

Roseline B

eni

ere, G

erard Subsol, William Puech

LIRMM, Univ. Montpellier 2, CNRS, 161 rue Ada, 34392, France

Gilles Gesqui

ere

LSIS, Aix-Marseille University, CNRS, IUT, BP 90178, 13637 Arles Cedex, France

Franc¸ois Le Breton

C4W, 219 rue Le Titien 34000 Montpellier, France

Keywords:

Remeshing, Quadrangular mesh, Quads quality, Parametrization.

Abstract:

In this paper we present a method to decompose a 3D triangular mesh into a set of quadrangulated patches.

This method consists in merging triangles to obtain quads. The quads are then grouped together to compose

quadrangulated areas and patches. Unlike many methods of remeshing, this method does not move the vertices

of the original triangular mesh. Quadrangulated patches extracted can then be used as a support of a parametric

function or of a subdivision scheme.

1 INTRODUCTION

In Computer Aided Design (CAD), numerical calcu-

lation or simple data exchange, it may be necessary

to discretize a 3D object to obtain a triangular mesh.

However, for many applications, a parametric repre-

sentation of these objects must be found. This topic

has been studied for many years. One way to solve

this problem is to calculate quadrangulated patches

which are then used to support parametric surfaces,

as shown in (Krishnamurthy and Levoy, 1996).

However, ﬁnding quadrangulated patches may be

useful for other applications. Thus (Arden, 2001)

shows the importance of these patches to use subdi-

vision methods, as the Catmull-Clark algorithm (Cat-

mull and Clark, 1978). The decomposition into quad-

rangulated patches can also be used for Finite Ele-

ments methods (Frey and George, 1999). Finally, in

the context of reverse engineering where we want to

ﬁnd a CAD model composed of parametric surfaces,

searching such patches is essential (Bommes et al.,

2009a).

This paper is focused on this problem with the

three following constraints:

• The original vertex positions of the 3D triangu-

lar mesh must be preserved and new vertex must

not be added. We assume indeed that these po-

sitions were determined by metrology, or were

computed directly from discretized CAD models

or were generated by numerical computation.

• The edges of the quadrangulated mesh must be

derived from the triangulated mesh (see Figure

1(b)). This ensures that the ﬁnal mesh will not

contain any incoherent junction, like, for exam-

ple, a T-junction where two edges cut themselves

in a point which is not a vertex of the mesh.

• The quadrangulated mesh must be decomposed

into patches which are rectangular grids with the

same number of rows for each column (see Figure

1(c)). This will then allow us to encode the object

in a standard format used in CAD as IGES (Initial

Graphics Exchange Speciﬁcation).

A study of existing methods is proposed in Section

2 and shows some of their limitations. A new method

of decomposition into quadrangulated patches is pre-

sented in Section 3. Some results are shown in section

4, and future work is explored in Section 5.

Bénière R., Subsol G., Puech W., Gesquière G. and Le Breton F. (2010).

DECOMPOSITION OF A 3D TRIANGULAR MESH INTO QUADRANGULATED PATCHES.

In Proceedings of the International Conference on Computer Graphics Theory and Applications, pages 96-103

DOI: 10.5220/0002833900960103

 SciTePress

(a) (b) (c)

Figure 1: Extraction of quadrangulated patches: a quadran-

gulated mesh is computed from the triangulated mesh (b).

The quadrangulated mesh is then decomposed into patches

(c).

2 PREVIOUS WORK

We choose to classify the methods for creating a

quadrangulated mesh from a triangulated mesh into

the three following classes.

2.1 The Remeshing Algorithms

In these methods, the position of the vertices are

not preserved. The idea of quadrangulated remesh-

ing is not recent (see for example (Hormann and

Greiner, 2000)) but new methods called “Quad dom-

inant remeshing” have emerged these last years. In

2003, Alliez and al. (Alliez et al., 2003) propose to

compute the principal directions at each regular point

of the surface. The curvature lines which are the in-

tegral lines of the principal directions allow to draw a

quadrangulated grid on the surface. This method has

been extended and for example, Dong and al. pro-

posed to use harmonic functions (Dong et al., 2005).

A synthesis of these methods is presented in (Alliez

et al., 2007) and recent algorithms can be found in

(Bommes et al., 2009b), (Lai et al., 2009), (Dong

et al., 2006) or (Huang et al., 2008). Notice that

many papers mention the T-junction problem which

requires a post-processing to avoid inconsistencies in

the resulting meshes.

2.2 The Advancing Front Algorithms

The most representative method is Q-Morph (Owen

et al., 1998). The idea is to propagate the construc-

tion of quads from the outlines to the center of the

triangulated mesh. The resulting quads are based on

the edges of the triangulated mesh. However, they are

smoothed and their vertices are not anymore similar

to the original ones. Furthermore, this method raises

some problems in the case of closed meshes and re-

cently a solution has been proposed (Miyazaki and

Harada, 2009). In this method, the authors segment

the mesh into areas, based on the vertex normals and

they apply the Q-Morph method to these areas.

2.3 The Merging Algorithms

These methods come from the numerical analysis

ﬁeld. Their aim is to merge triangles of the mesh into

quads to perform numerical computing, in general by

Finite Element methods. Most of these algorithms

work only with 2D meshes but (Borouchaki et al.,

1997) presents a simple and modular presents for 3D

meshes. This method is based on triangle merging

with respect to a quality coefﬁcient. As (Tarini et al.,

2010), we have adapted and developed this idea to ob-

tain the ﬁrst step of our decomposition algorithm.

2.4 Conclusion

All these methods create quadrangulated meshes

which are not composed of the original vertices and

edges of the initial triangular mesh. Furthermore,

they do not lead to a direct and explicit decomposi-

tion into patches even if some methods as (Eppstein

et al., 2008) have been proposed.

In this paper, we present a straightforward method

that combines both steps: quadrangulation and de-

composition into patches.

3 OUR METHOD

In this section we describe a new method of decompo-

sition into quadrangulated patches which is composed

of three steps:

• a coefﬁcient which deﬁnes the quality of a quad

created by merging two triangles is computed for

each pair of adjacent triangles;

• quadrangulated areas are then built by aggregat-

ing the quads according to values of the quality

coefﬁcient;

• quadrangulated areas are then decomposed into

quadrangulated patches.

3.1 Quads Creation

The ﬁrst step consists in creating quads based on the

triangulated mesh. These quads should be built using

only vertices and edges of the original mesh. A quad

is deﬁned by merging two adjacent triangles. A trian-

gle can lead to the creation of up to three quads, one

by edge, so a choice should be made.

As in (Borouchaki et al., 1997), this choice should

be based on a quality coefﬁcient computed for each

pair of adjacent triangles. In our method, we want to

give high priority to quads which are similar to planar

rectangles. In this case, each angle α

of the quad is

DECOMPOSITION OF A 3D TRIANGULAR MESH INTO QUADRANGULATED PATCHES

close to

and the dihedral angle φ between the two

triangles constituting the quad is close to π (see Figure

2). So, a quality coefﬁcient Q can be deﬁned by:

Q =







2π if φ < φ

min

∑

i=1

− α

| else .

(1)

Thus, this coefﬁcient equals to the average differ-

ence between each angle and

. Thus a quad which is

similar to a rectangle will have a coefﬁcient close to

(a)

(b)

Figure 2: (a) The quality coefﬁcient Q is computed with the

(in red) which are the angles at the quad vertices and the

dihedral angle φ (in blue). (b) A large dihedral angle and α

far from

implies a “bad” quality.

Moreover, if the dihedral angle is smaller than a

tolerance φ

min

, the quad will be ﬂagged as “incorrect”

as in Figure 2(b). Similarly, the quads which have a

quality coefﬁcient greater than the tolerance Q

max

are

not used to build quadrangulated areas.

3.2 Extraction of Quadrangulated

Areas

The aim of this step is to extract quadrangulated areas

using the quality coefﬁcient presented in the previous

section.

In the ﬁrst step, to initialize the process, the quad

with the best quality coefﬁcient is chosen. The quad-

rangulated area is propagated iteratively by adding at

each step the quad having the best quality coefﬁcient

among the neighborhood of the area in construction.

To ﬁnd this quad, all potential quads containing an

adjacent triangle with an edge of the area outline are

examined. For example, in Figure 3(b), the hatched

triangles are examined to ﬁnd the next quad of the

quadrangulated area.

The propagation is stopped when there is no

neighboring triangles anymore, or if the triangle is

isolated, or if the neighboring triangles can only cre-

ate quads with a quality coefﬁcient larger than Q

max

When an area is ﬁnalized, a new area is initialized,

with the quad having the best quality coefﬁcient in the

part of the triangulated mesh not used yet.

Initialization FinalizationStep n

(a)

(b)

(c)

Figure 3: Iterative extraction of a quadrangulated area: ini-

tialization with the quad having the best quality coefﬁcient

(a); at each step a quad is added (b); the process stops when

there is no quad to be added anymore (c).

Thus from a triangulated mesh, one or more quad-

rangulated areas are obtained. For example, only one

quadrangulated area has been extracted from the mesh

in Figure 4. However, all triangles are not used, the

left triangles correspond to isolated triangles or tri-

angles which can only lead to quads with a quality

coefﬁcient larger than Q

max

Figure 4: Extraction of a quadrangulated area from a trian-

gulated mesh. The left triangles do not enable to create a

quad having a good quality.

3.3 Decomposition into

Quadrangulated Patches

After the quadrangulated area process, a decomposi-

tion into sub-areas which are called “rectilinear poly-

gons” begins. For this purpose, a unique position is

assigned to each quad. This position consists in a line

number and a column number which will allow to de-

ﬁne the rectilinear polygons.

The quad having the best quality coefﬁcient is

chosen in the quadrangulated area. It is labeled with

the position (0, 0). Positions are then propagated to

its four neighbors, as in the Figure 5.

(1,1)

(0,1)

(1,0)

(0,1)

(0,0)

(1,0)

Initialization Step 1 Step n

(a)

(b)

(c)

(0,-1)

(-1,0)

(0,-1)

(1,-1)

(-1,1)

(0,0)

(-1,-1)

(-1,0)

Figure 5: Propagation of the position from the ﬁrst quad to

its neighbors.

When a position is assigned to each quad, a recti-

linear polygon is deﬁned using the positions to store

the quads at a correct place in a regular grid.

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

Creating the rectilinear polygon by assigning a po-

sition to each quad in relation to the position of its

neighbors can lead to ambiguities. Thus, the ﬁrst cho-

sen quad in Figure 6 is quad 1, the positions of quads

2, 3, 4, 5 and 7 are easily deduced afterward. The

problem is with the quad 6 which would have both

the position (1, 2) as a neighbor “down” of the quad

5 and the position (0, 2) as a neighbor “up” of the

quad 7. Furthermore, these two positions are already

assigned. There will be another problem with quad

11 which has two different positions assigned, one as

the “right” neighbor of quad 8 and one as the “right”

neighbor of quad 9.

Such ambiguities occur when the vertices of the

quadrangulated area are not of valence 4. In the ex-

ample of Figure 6, a valence 3 vertex and a valence 5

vertex raise the position attribution problems.

31 5

(1,0)

(0,2)

(1,1)

(1,2)

(??,2)

(0,1)(0,0)

Valence 3

Valence 5

Figure 6: Decomposition into “rectilinear polygons” with

ambiguity positions with the quads 6 and 11.

To avoid this, some tests were added to check if

two quads have not the same position or if two po-

sitions are not assigned to the same quad. If any of

these cases occur, the rectilinear polygon is decom-

posed into two polygons. Thus the quadrangulated

mesh of Figure 6 is decomposed into three rectilinear

polygons as in Figure 7.

Rectilinear polygons containing only one quad are

not kept, like the rectilinear polygon with the single

quad 11 in Figure 7. Its two triangles remain then in

the triangulated mesh.

(0,0) (0,1) (0,2)

(0,3)

(0,4)

(0,0)

(0,1)

(0,2)

(1,3)

(0,3)

(1,2)

(0,0)

Figure 7: Decomposing the quadrangulated area into 3 rec-

tilinear polygons.

The last step enables to decompose the rectilin-

ear polygons into patches, which are rectangular grids

having the same number of lines for each column.

An iterative method is used to perform this. Ini-

tially, the patch with the greatest number of quads is

computed. The quads of the patch are removed from

the rectilinear polygon. A new patch with the great-

est number of quads can be then searched in the new

rectilinear polygon. The process is stopped when no

quad is left in the rectilinear polygon.

To ﬁnd the patch with the greatest number of

quads in the rectilinear polygon, each quad of the rec-

tilinear polygon is examined. For a quad, all patches

having this quad at “left upper corner” are computed.

Such a computation of patches is based on browsing

along only two directions(→ and ↓), because the two

other directions were already examined by browsing

from the previous quads. The longest line (→) from

the quad is computed. Then, the number of lines hav-

ing the same length existing down (↓) is determined.

In Figure 8, from the quad q, the longest possible line

includes ﬁve quads, and lines of ﬁve quads are pos-

sible only on both lines. Finally, the patch with the

greatest number of quads among all patches computed

for each quad is selected.

Figure 8: Patch construction in a rectilinear polygon from

quad q.

Nevertheless, this method does not guarantee that

the number of patches is minimal at the end of the

process. Thus in Figure 9, extracting initially the

patch with the greatest number of quads (hatched

in blue), the rectilinear polygon is decomposed into

three patches whereas only two would be necessary

to cover the whole it.

Figure 9: Case where our method does not give an optimal

covering: we obtain three patches while two would be suf-

ﬁcient.

However we decide to keep this simple approach

even if some methods exist to optimize the number of

patches dissecting the rectilinear polygon as for ex-

ample in (Soltan and Gorpinevich, 1993).

Finally, the three steps lead to three quadrangu-

lated patches, shown in Figure 10. Notice that a part

of the triangulated mesh is not used. This is due to

isolated triangles, quads of which Q > Q

max

, or quads

DECOMPOSITION OF A 3D TRIANGULAR MESH INTO QUADRANGULATED PATCHES

Quadrangle with

Triangle isolated

Patch extracted 1

Patch extracted 2

Patch extracted 3

Quadrangle isolated

bad quality

Figure 10: Decomposition into quadrangulated patches

from a triangulated mesh.

isolated during the creation of the rectilinear poly-

gons.

4 EXPERIMENTAL RESULTS

Our method has been implemented in the software 3D

Shop of the C4W

. This software gives efﬁcient devel-

opment tools for 3D modeling and visualization

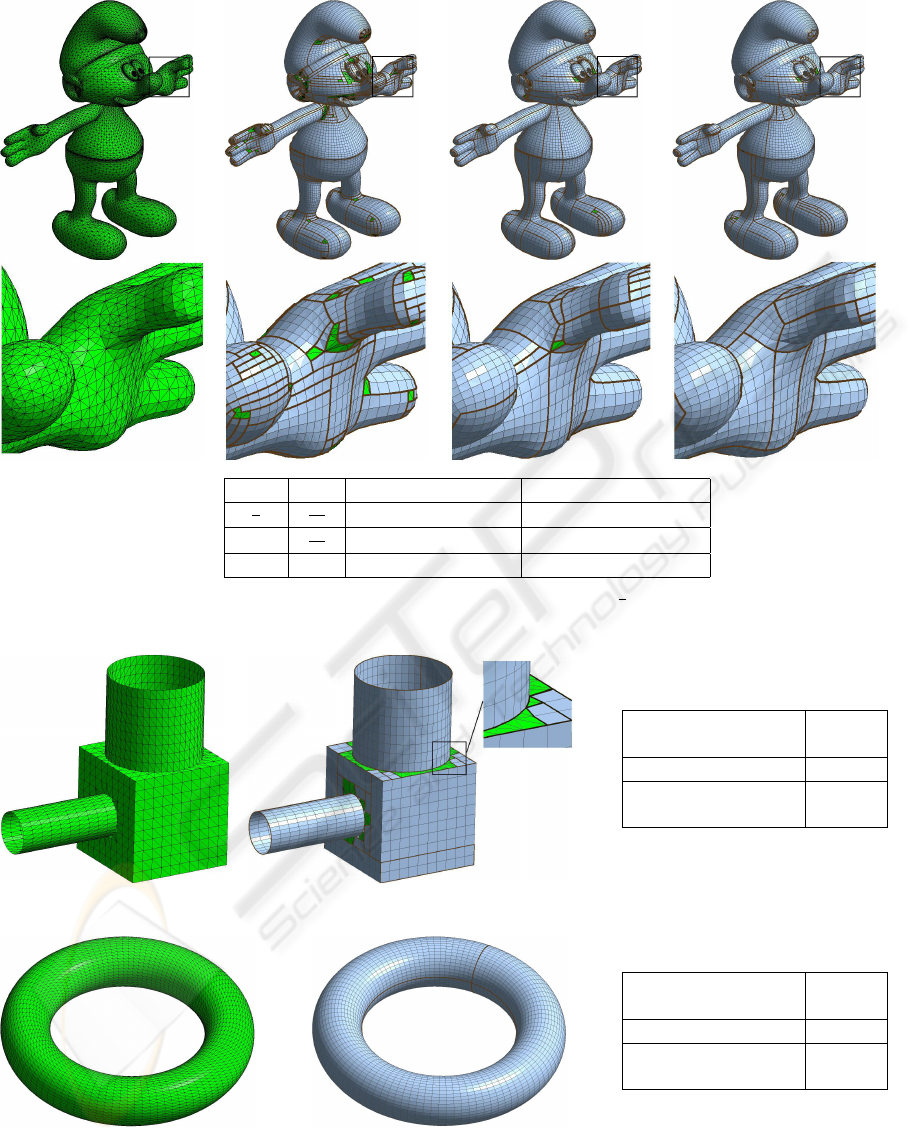
Figures 11 (Bunny), 12 (Face), 13 (Fandisk), 14

(Smurf

), 15 (CubeCylinders) and 16 (Torus) show

some results obtained on triangulated meshes coming

from various sources as CAD for CubeCylinders and

Torus, infography for Face and Smurf or 3D digitiza-

tion for Bunny and Fandisk. Each result is constituted

of the extracted quadrangulated patches (in blue) and

of remaining triangles (in green). Table 1 gives for

each mesh, the number of triangles, the number of ex-

tracted patches and the covering percentage that cor-

responds to the percentage of original triangles cov-

ered by quadrangulated patches.

On Bunny, Face and Fandisk, the quadrangulated

patches cover a large part of the mesh. That enables to

obtain a reduction factor between the triangle number

and the patch number which reaches 30. Effective

coding in CAD format based on the face concept (like

IGES) can be envisaged.

Nevertheless, some patches have a small size and

to cover 80% of the 5,590 triangles of the mesh Face,

335 patches are used. The decomposition of some

areas into small patches comes from a few triangles

or quads which are isolated and lead to decompose a

large potential patch into several smaller ones.

C4W is a company which develops innovative

CAD solutions and support this Ph.D. Thesis work

(http://www.c4w.com)

www.c4w.com/3d-cad-software.html

http://www.3dvalley.com/3d-models/characters

To avoid this and to create larger patches, we ex-

perimented different values for the parameters Q

max

and φ

min

because these thresholds may limit the prop-

agation process during the construction of quadran-

gulated areas. The values Q

max

and φ

min

were em-

pirically ﬁxed to respectively

and

5π

, for all tests

except on the mesh Smurf.

For the mesh Smurf in Figure 14, the value Q

max

is ﬁxed successively to

, π and 2π. The threshold

min

has been modiﬁed in the last case to 2π: in this

case, all potential quads have been then considered.

Figure 14, with the mesh Smurf, which have 64,320

triangles, shows the patches evolution. Some areas

like the eyes, the hands or the shoulder contain many

triangles which are not used. The number of unused

triangles decreases when the thresholds are modiﬁed.

The number of patches decreases too and the cover-

ing percentage increases. These new results arises

because the patch shapes can change dramatically by

adding only one new quad as in Figure 14.

However, it is necessary to take care of the quad-

rangulated patches which can then contain some

quads with low quality. This may engender problems

to some applications, for example in numerical calcu-

lation. Moreover even when we set both thresholds

to 2π, there are always left triangles. Indeed, there

are triangles isolated in the quadrangulated areas con-

struction and quads isolated in the rectilinear poly-

gons construction. On the quadrangulated areas con-

taining many vertices which are not valence 4, these

quads can very be numerous and may lead to lots of

small rectilinear polygons.

Finally, we have tested our method on 3D simple

objects, like the union of a cube and two cylinders

(Figure 15). The result of the decomposition from

the mesh CubeCylinders, is satisfying because more

than 95% of the mesh is covered with only 21 patches

which corresponds to a reduction factor of more than

130. However in the case of a simply torus like Figure

16, our method ﬁnds one patch which covers 100%

of the object. The method is really adapted to CAD

meshes composed by simple primitives. In fact our

method has good result on the CAD mesh because

the discretization of the mesh has often a ﬁrst step of

quadrangulation which was then triangulated.

5 CONCLUSIONS AND

PERSPECTIVES

In this paper, we have presented a method enabling to

decompose 3D triangulated meshes into quadrangu-

lated patches, without modifying the vertex position.

Our method is based on merging adjacent triangles to

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

100

Table 1: Results on different 3D triangular meshes.

Mesh Triangles in mesh Extracted patches Covering percentage

Bunny 69,451 1,932 89.98%

Face 5,590 335 80.32%

Fandisk 23,964 720 88.66%

Smurf 64,320 931 91.39%

CubeCylinders 2,608 21 95.47%

Torus 9,384 1 100%

Triangles in the mesh 69,451

Extracted patches 1,932

Covering percentage 89.98%

Figure 11: Original mesh and result for: Bunny.

Triangles in the

mesh

5,590

Extracted patches 335

Covering percent-

age

80.32%

Figure 12: Original mesh and result for: Face.

Triangles in the

mesh

23,964

Extracted patches 720

Covering percent-

age

88.66%

Figure 13: Original mesh and result for: Fandisk.

DECOMPOSITION OF A 3D TRIANGULAR MESH INTO QUADRANGULATED PATCHES

101

max

min

Number of patches Covering percentage

5π

931 91.39%

5π

519 98.52%

2π 2π 502 98.56%

Figure 14: The mesh Smurf with a zoom mesh and the obtained results with Q

max

, π and 2π (left to right). The number

of patches decreases and their sizes increase. So the covering with the decomposition is better on this example.

Triangles in the

mesh

2,608

Extracted patches 21

Covering percent-

age

95.47%

Figure 15: Original mesh and result for: CubeCylinders.

Triangles in the

mesh

9,384

Extracted patches 1

Covering percent-

age

100%

Figure 16: Original mesh and result for: Torus.

create quads satisfying a quality criterion. Quads are

then aggregated into quadrangulated areas which are

ﬁnally decomposed into patches.

This decomposition into quadrangulated patches

can be used in many applications such as the creation

of parametric surfaces, subdivision, or the numerical

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

102

calculation.

Comparison with other existing methods, quad-

rangulation and decomposition ones, should be made.

The proposed method can be improved in each

of its three steps. First, deﬁning other quality coef-

ﬁcients could improve the extraction of quadrangu-

lated areas. According to computed parameters on the

complete mesh, averages of angles computed for all

the vertices seems to be a good way. The constraints

can also be adjusted according to its local “shape”, by

relaxing for example the constraints of the dihedral

angle in the most curved part of the object.

Other propagation algorithm for the creation of

quadrangulated areas, can be proposed or the research

of rectilinear polygons can be optimized. The objec-

tive of these two modiﬁcations would be to decrease

the number of isolated triangles.

Another possible improvement would be to avoid

the step of extracting rectilinear polygons, and to de-

compose directly quadrangulated areas into patches.

This would enable to optimize globally the process

and to decrease the number of patches constituted by

a single quad which do not belong to the ﬁnal decom-

position.

A last step of patch merging could be added and

it would enable to group two patches in only one, in-

tegrating if it is necessary adjacent isolated quads. If

it does not improve the percentage of covering, it will

decrease the number of patches of the decomposition.

Finally, some feature lines could be used, as

the “ridge lines” to deﬁne potential boundaries for

patches. The decomposition would be then optimized

using this knowledge as it is done in several remesh-

ing algorithms.

ACKNOWLEDGEMENTS

The authors want to thank the C4W company and the

Association Nationale de la Recherche et de la Tech-

nologie (ANRT) for their ﬁnancial support.

REFERENCES

Alliez, P., Cohen-Steiner, D., Devillers, O., Lvy, B., and

Desbrun, M. (2003). Anisotropic polygonal remesh-

ing. ACM Transactions on Graphics, SIGGRAPH

2003 Conference Proceedings, 22(3):485–493.

Alliez, P., Ucelli, G., Gotsman, C., and Attene, M.

(2007). Recent advances in remeshing of surfaces.

In Shape Analysis and Structuring, pages 53–82.

Springer Berlin Heidelberg.

Arden, G. (2001). Approximation Properties of Subdivision

Surfaces. PhD thesis, University of Washington.

Bommes, D., Vossemer, T., and Kobbelt, L. (2009a). Quad-

rangular parametrization for reverse engineering. Lec-

ture Notes in Computer Science (to appear).

Bommes, D., Zimmer, H., and Kobbelt, L. (2009b).

Mixed-integer quadrangulation. ACM Trans. Graph.,

28(3):1–10.

Borouchaki, H., Frey, P. J., and George, P. L. (1997). Mail-

lage de surfaces param

etriques. Partie III: El

ements

quadrangulaires. 325(1):551–556.

Catmull, E. and Clark, J. (1978). Recursively generated

B-spline surfaces on arbitrary topological meshes.

Computer-Aided Design, 10(6):350–355.

Dong, S., Bremer, P.-T., Garland, M., Pascucci, V., and

Hart, J. C. (2006). Spectral surface quadrangulation.

ACM Trans. Graph., 25(3):1057–1066.

Dong, S., Kircher, S., and Garland, M. (2005). Har-

monic functions for quadrilateral remeshing of arbi-

trary manifolds. Computer Aided Geometry Design,

Special Issue on Geometry Processing, 22(5):392–

423.

Eppstein, D., Goodrich, M. T., Kim, E., and Tamstorf, R.

(2008). Motorcycle graphs : Canonical mesh parti-

tioning. Comput. Graph. Forum, 27(5):1477–1486.

Frey, P. J. and George, P. L. (1999). Maillage : Applications

aux

ements ﬁnis. Hermes Science.

Hormann, K. and Greiner, G. (2000). Quadrilateral remesh-

ing. In Girod, B., Greiner, G., Niemann, H., and Sei-

del, H.-P., editors, Proceedings of Vision, Modeling,

and Visualization 2000, pages 153–162, Saarbr

ucken,

Germany.

Huang, J., Zhang, M., Ma, J., Liu, X., Kobbelt, L., and Bao,

H. (2008). Spectral quadrangulation with orientation

and alignment control. ACM Trans. Graph., 27(5):1–

Krishnamurthy, V. and Levoy, M. (1996). Fitting smooth

surfaces to dense polygon meshes. In Proceedings of

SIGGRAPH 96, pages 313–324.

Lai, Y.-K., Kobbelt, L., and Hu, S.-M. (2009). Feature

aligned quad dominant remeshing using iterative lo-

cal updates. Computer-Aided Design (to appear).

Miyazaki, R. and Harada, K. (2009). Transformation of

a closed 3D triangular mesh to a quadrilateral mesh

based on feature edges. IJCSNS International Journal

of Computer Science and Network Security, 9(5).

Owen, S. J., Staten, M. L., Canann, S. A., and Saigal, S.

(1998). Advancing front quadrilateral meshing using

triangle transformations. 7th International Meshing

Roundtable, pages 409–428.

Soltan, V. and Gorpinevich, A. (1993). Minimum dissec-

tion of a rectilinear polygon with arbitrary holes into

rectangles. Discrete and Computational Geometry,

9(1):57–59.

Tarini, M., Pietroni, N., Cignoni, P., Panozzo, D., and

Puppo, E. (2010). Practical quad mesh simpliﬁcation.

Computer Graphics Forum, 29(2):To appear.

DECOMPOSITION OF A 3D TRIANGULAR MESH INTO QUADRANGULATED PATCHES

103