OBJECT DETECTION USING PICTORIAL STRUCTURE OF

GABOR TEMPLATE

Babak Saleh and Mohammad Rastegari

Computer Vision Group, Institute for Research in Fundamental Sciences (IPM), Tehran, Iran

Keywords:

Gabor wavelet, Deformable model, Spanning tree, Dynamic programming, Pictorial structure.

Abstract:

Object detection methods are divided into two main branches: In the global approach one extracts low level

features and uses machine learning techniques. In the part-based approach one uses deformable templates. We

present a Hybrid approach for constructing a deformable template for modeling and detection. Initially one

applies Gabor wavelet ﬁlters to extract low level features and constructs graphs which resemble shock graphs.

A minimum spanning tree (MST) is extracted and is called the pictorial graph. It is used for matching. The

pictorial graph is suitable for preserving the visual appearance of the shape of the object and for accommo-

dating shape variances. In this hybrid approach we maintain the generality of the global and the efﬁciency of

part-based approaches. Our algorithm has been applied to a set of test cases and the result shows improved

performance as compared to standard object detection methods that do not rely on human intervention.

1 INTRODUCTION

There are two approaches to object detection namely

the global and the part-based ones. In the Global ap-

proach to object detection features are extracted from

raw images and machine learning is used to make

models for particular objects (Zhang et al., 2008; Wu

et al., 2009; Amira and Farrell, 2005). In the part-

based approach (Ramanan and Sminchisescu, 2006;

Ioffe and Forsyth, 2001; Kohandani et al., 2006;

E. Yen, 2005; Lowe, 1991) an object is represented as

a set of its parts, and it is represented as a graph with

various parts connected by the edges of the graph.

In the global approach gabor wavelets are applied

globally to extract a template from a class of objects

(e.g., bicycles, cars etc.) For object detection the tem-

plates are applied to the given image. A propitious

feature of the global approach is that it lends itself

to learning algorithms well. A difﬁculty with this

approach is that it is very rigid and cannot accom-

modate shape variances. The part-based approach

improves the performance and alleviates the rigidity

problem of the global method but the templates had

to be designed separately and rely strongly on human

intervention. Computational speed is another issue in

the global approach to object detection. The graph

models are usually simple trees in the part-based ap-

proach and economize signiﬁcantly on the compu-

tational time as compared to the global one. Dy-

namic programming, belief propagation algorithms

can be applied to accelerate the computation in the

part-based method (Kohandani et al., 2006).

In our hybrid approach, we initially apply gabor

wavelets to extract templates as in the global ap-

proach. A key new feature is that we modify the

template by ﬁrst assigning a graph to it and then ex-

tracting a minimum spanning tree (MST) from the

graph. With the MST we can apply a method sim-

ilar to that of the part-based approach for the detec-

tion of an object in a given image. It should be noted

that the tree structure that was extracted from the tem-

plate allows for the incorporation of shape variances

in a given class and ameliorates the corresponding

problem which one normally encounters in the global

method. Our hybrid approach is computationally ef-

ﬁcient since we are essentially dealing with a tree

structure as in the part-based method. Furthermore

the learning processes in the proposed algorithm do

not suffer from the shortcomings of the part-based

method and are easily implementable as in the global

approach.

In Section 2 the template extraction method that

we used is described and is based on (Wu et al., 2009).

The extraction of the MST corresponding to a given

class is given in Section 3. The object identiﬁcation

process is described in Section 4 and the empirical re-

sults are presented in Section 5.

396

Saleh B. and Rastegari M. (2010).

OBJECT DETECTION USING PICTORIAL STRUCTURE OF GABOR TEMPLATE.

In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 396-400

DOI: 10.5220/0002834203960400

 SciTePress

2 TEMPLATE EXTRACTION

We extract a generative template consisting of small

components. These small elements are special type of

wavelets. Mathematically a gabor function is one of

the form:

G(x,y) ∝ e

{−[(

)

]}

(1)

The general form of gabor wavelets are obtained

by the translation, rotation and dilation of G; In fact

representing a rotation and translation in the form:

˜x = (x

− x)cosα − (y

− y)sinα,

˜y = (x

− x)sinα − (y

− y)cosα.

Then the general gabor wavelet with (x,y) as the cen-

tral position, s the scale parameter and orientation α

is given by:

(x,y,s,α)

G( ˜x/s, ˜y/s)

In Figure 1 an artiﬁcial image and its gabor transform

are shown.

(a) (b)

Figure 1: An artiﬁcial image and its gabor transform. (a)An

artiﬁcial input image. (b)Output ﬁeld, resulted by applying

gabor function.

For template extraction we ﬁrst ﬁx a category con-

sisting of one class of objects, e.g. passenger cars.

The samples have the same parameters such as pose,

size, orientation, etc. Then we apply gabor ﬁlters in

every possible combinations of location and orienta-

tion with a ﬁxed scale on the training image set. The

output is a set of coefﬁcients which are computed in

the familiar way as an inner product. A template is

selected by a voting algorithm, more precisely known

as the Shred Sketch Algorithm, applied to the outputs

of gabor ﬁlters as in (Wu et al., 2009). A selected

output is referred to as a component of a generative

template.

3 EXTRACTING MST

STRUCTURE

The template graph is a weighted complete graph with

nodes (or vertices) corresponding to the wavelet coef-

ﬁcients. The weight assigned to an edge is the ”Eu-

clidean distance” between the centers of the wavelets

whose coefﬁcients correspond to the vertices of the

edge. This is a very complex graph we extract a mini-

mum spanning tree (MST) by which we mean a span-

ning tree such that the sum of the weights is a mini-

mum. In general specifying an MST has O(n

) com-

plexity. To reduce the amount of calculation we con-

sider the Delaunay triangulation of the plane with the

given nodes. This is no longer a complete graph and

we retain the weights for the surviving edges. By a

standard method (Kruskal, 1956) we extract an MST

from this graph as shown Figure 2. The complexity

of this operation is O(n logn).

Having modiﬁed the active template structure to

that of an MST we tested the algorithm on several

shape categories to ensure that it provides a faithful

representation of the class of objects in the category.

Five examples are shown in Figure 2. Notice that the

MST’s are “good” representations of the objects.

4 MATCHING ALGORITHM

In this section we are going to explain how we can

ﬁnd the best matching of the extracted template (or

MST) to an object in a given image. In order to

ﬁnd this best matching we will modify a well-known

method (P.F. Felzenszwalb, 2000) for the efﬁcient

matching of pictorial structures. A pictorial structure

(Fischler and Elschlager, 1986) is a template given

by a number of parts with connections between them

(Figure 3(a)). This connection is elastic like a spring

and shrinks or dilates according to the movements of

the parts (Figure 3(b)). This form of connection gives

the parts the capability to change their location with

respect to each other in a deformation in a smooth

manner.

To quantify the “goodness” of a match we intro-

duce several quantities. Let l

be the 4-vector describ-

ing the location, scaling and orientation of a wavelet

coefﬁcient. Given an image I we want to deﬁne a cost

function (Global Matching Function) for a given pic-

torial structure which is a sum of both the cost for

ﬁtting this pictorial structure to an object in the im-

age and a deformation cost with respect to parts’ po-

sitions, their distances, rotations, and scales (Felzen-

szwalb and Huttenlocher, 2005). In other words the

cost function measures both how well each element

ﬁts the image data and how well the relative positions

of the elements agree with the model. Mathematically

the global matching function or cost on an image I is

expressed as

OBJECT DETECTION USING PICTORIAL STRUCTURE OF GABOR TEMPLATE

397

Figure 2: Extracted Templates and the corresponding MST. The ﬁrst row shows input templates consisting of gabor wavelets.

The second row is the result of applying MST on these templates.

(a) (b)

Figure 3: (a) Pictorial structure of Human body, different

parts and their connection are illustrated this picture de-

signed by (Borgefors, 1984) (b) Spring connection in a Pic-

torial Structure. It shows that in pictorial structure of a face

different parts can slightly change their positions. This pic-

ture designed by (Felzenszwalb and Huttenlocher, 2005).

L(I) = min



∑

)∈E

i j

) +

∑

∈V

(I, l

)



, (2)

where E is the edge set of the MST, d

i j

) is the

Euclidean distance between l

’s, m

(I, l

) represents

the distance between the wavelet l

and the wavelet

transform of the corresponding point in the image I,

and the min is taken over all possible matching.

The naive exhaustive search computation of L is

very inefﬁcient and its complexity is of the order

O(h

), where h is the number of possible location. In

(P.F. Felzenszwalb, 2000) the authors showed that if

the given pictorial structure is a tree, then one can ap-

ply a dynamic programming algorithm which reduces

the complexity to as low as O(h). The tree structure

helps represent the deformation cost of each element

as a function of its children’s costs. This method re-

sults in a recursive algorithm for the minimization

problem as follow: For every leaf node of this tree

it is sufﬁcient to ﬁnd the best location which has the

minimum matching cost. For other nodes one ﬁnds

the best place constrained by the children’s locations

which have been determined in the preceding itera-

tion. This recursive algorithm is summarized by the

equation 3

) = min



i j

) + m

(I, l

) +

∑

∈C

)



(3)

where C

is the set of children of j, B

) is the

best location for the children of j (represented by

the v

), which B

) is the best location of the j

part given its parent location l

. This recursive algo-

rithm reduces the complexity to O(h

). To achieve

a lower complexity we make use of the generalized

distance transform (GDT) (P.F. Felzenszwalb, 2004)

on the tree. GDT is a weighted version of usual dis-

tance transform (Borgefors, 1984; Borgefors, 1986).

We used expanded GDT in four dimensions: (x, y)

-components of the center of the gabor, s-scale pa-

rameter and r-orientation. Using the naive approach

ﬁnding the best conﬁguration has complexity O(h

and the dynamic programming approach (A. Amini,

1990) reduces it to O(h

n), where h is the number of

possible locations for each part and n is the number of

parts. In our application h is large (and n is relatively

small) which makes the computation infeasible. But

state of the art generalized distance transform reduces

the complexity to O(hn) or O(h) since n is a small

number independent of h.

5 RESULTS

In this section we present some experimental results

of our approach and a comparison is made with the

Active Basis methods (Wu et al., 2009). We imple-

mented our method with MATLAB on a PC with 1.8

GHz CPU and 512 MB RAM and selected 60 gabor

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

398

Figure 4: Qualitative results. The ﬁrst and fourth rows show input test images for different categories, taken from (Wu et al.,

2009), the second and ﬁfth rows are the results of the proposed method and the third and sixth rows show the results attained

by (Wu et al., 2009).

wavelets for the template. We used gabor bases at

8 orientations and 10 scales. Our experiments were

carried out on the database provided by (Wu et al.,

2009). Figure 4 shows a qualitative comparison where

the results of four test cases obtained by the pro-

posed and the Active Basis (Wu et al., 2009) methods

are shown. As one can see our method (the second

and ﬁfth rows) has qualitatively superior performance

relative to the Active Basis one (the third and sixth

rows). Figure 5 demonstrates a quantitative compar-

ison. The RoC curves of the two test cases for three

methods are shown. The RoC curve based on the pro-

posed method showed signiﬁcant improvement rela-

tive to Active Basis and the Texture Mask methods

(Wu et al., 2008). We did not compare with the part-

based method because the latter approach requires hu-

man intervention.

6 CONCLUSIONS

A new method for object detection was presented.

The proposed algorithm is a hybrid method that com-

bines a generative template similar to the global ap-

proach to object detection and a fast algorithm for ﬁt-

ting this template into images in order to achieve ob-

ject detection. This matching algorithm is based on

dynamic programming algorithm.

The novelty and advantages of the proposed

method are

1. It has the ﬂexibility of accommodating visual

variances as in the part-based approach.

2. It lends itself easily to learning algorithms as in

the global approach.

3. It does not require human intervention as in the

part-based approach.

4. Its computational complexity is low as in the part-

based approach.

ACKNOWLEDGEMENTS

The authors would like to thank Prof. Mehrdad Mir-

shams Shahshahani for his great support, valuable

discussions and supervision.

OBJECT DETECTION USING PICTORIAL STRUCTURE OF GABOR TEMPLATE

399

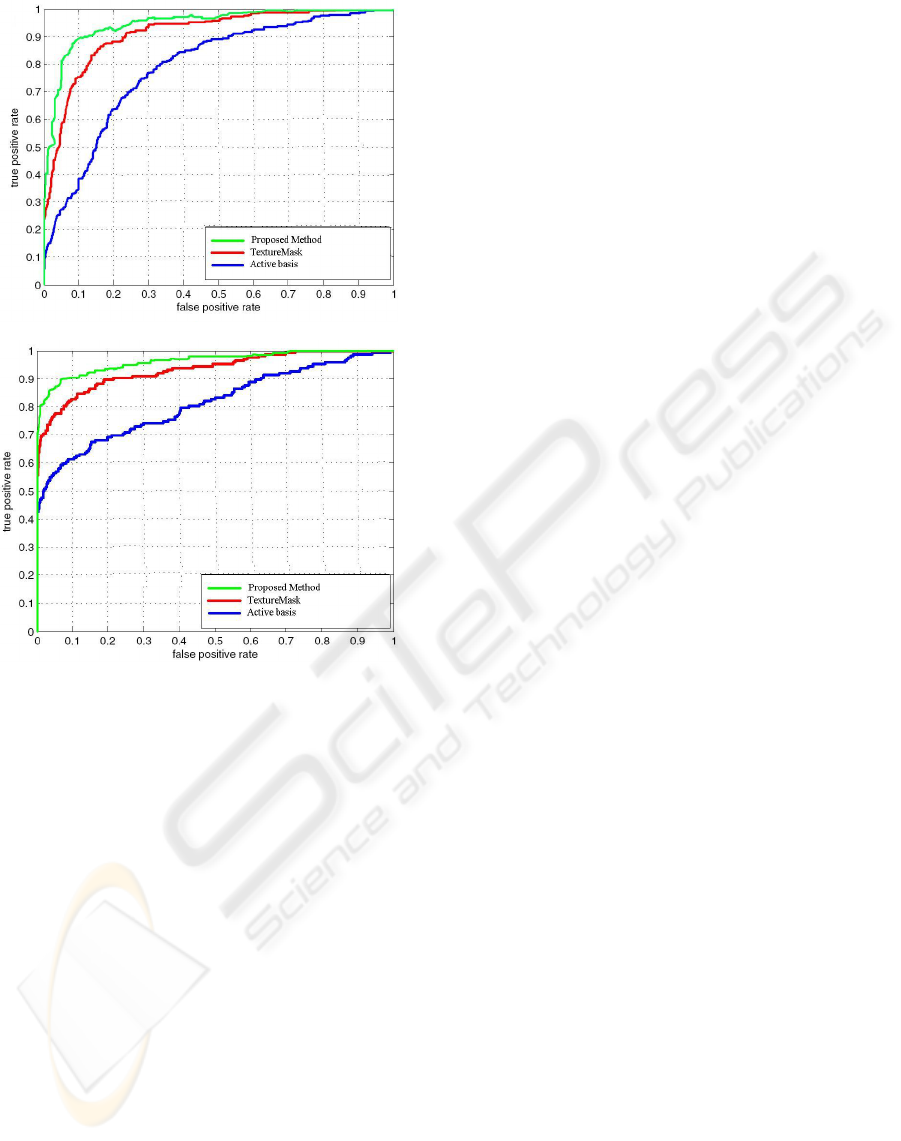
(a)

(b)

Figure 5: (a) RoC curves for Car samples, in the front

viewpoint,(b) RoC curves correspondent to Motorbike sam-

ples.

REFERENCES

A. Amini, T. Weymouth, R. J. (1990). Using dynamic pro-

gramming for solving variational problems in vision.

In Vol. 12, No. 9, pp. 855-867. PAMI.

Amira, A. and Farrell, P. (2005). An automatic face recog-

nition system based on wavelet transforms. In ISCAS

(6), pages 6252–6255.

Borgefors, G. (1984). Distance transformations in arbitrary

dimensions. In Vol. 27, No. 3, pp. 321-345. CVGIP.

Borgefors, G. (1986). Distance transformations in digital

images. In Vol. 34, No. 3, pp. 344-371. CVGIP.

E. Yen, A. S. (2005). Image recognition via deformable

template. statistical methodology. In pp. 213-225. Sta-

tistical Methodology.

Felzenszwalb, P. F. and Huttenlocher, D. P. (2005). Pic-

torial structures for object recognition. International

Journal of Computer Vision, 61(1):55–79.

Fischler, M. and Elschlager, R. (1986). The representation

and matching of pictorial structures. In Vol. 22, No. 1,

pp. 67-92. IEEE Trans. On Computers.

Ioffe, S. and Forsyth, D. A. (2001). Mixtures of trees for

object recognition. In CVPR (2), pages 180–185.

Kohandani, A., Basir, O. A., and Kamel, M. S. (2006). A

fast algorithm for template matching. In ICIAR (2),

pages 398–409.

Kruskal, J. (1956). On the shortest spanning subtree of a

graph and the traveling salesman problem. In Pro-

ceedings of the American Mathematical Society.

Lowe, D. G. (1991). Fitting parameterized three-

dimensional models to images. IEEE Trans. Pattern

Anal. Mach. Intell., 13(5):441–450.

P.F. Felzenszwalb, D. H. (2000). Efﬁcient matching of pic-

torial structures. In IEEE Conference on Computer

Vision and Pattern Recognition.

P.F. Felzenszwalb, D. H. (2004). Distance transforms of

sampled functions. In Cornell Computing and Infor-

mation Science Technical Report TR2004-1963.

Ramanan, D. and Sminchisescu, C. (2006). Computer Vi-

sion and Pattern Recognition, 2006 IEEE Computer

Society Conference on, volume 1.

Wu, Y., Si, Z., Gong, H., and Zhu, S. (2009). Learning ac-

tive basis model for object detection and recognition.

In IJCV.

Wu, Y. N., Si, Z., Gong, H., and Zhu, S.-C. (2008). Active

basis model, shared sketch algorithm, and sum-max

maps. IJCV.

Zhang, L., Gong, H., Wu, T., and Dong, J. (2008).

Deformable template combining alignable and non-

alignable sketches. In ICPR, pages 1–4.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

400