CONTROLLED AND ADAPTIVE MESH ZIPPERING

Stefano Marras

, Fabio Ganovelli

, Paolo Cignoni

, Riccardo Scateni

and Roberto Scopigno

University of Cagliari, Italy

ISTI-CNR, Italy

Keywords:

Zippering, Stitching, 3D scanning.

Abstract:

Merging meshes is a recurrent need in geometry modeling and it is a critical step in the 3D acquisition pipeline,

where it is used for building a single mesh from several range scans. A pioneering simple and effective

solution to merging is represented by the Zippering algorithm (Turk and Levoy, 1994), which consists of

simply stitching the meshes together along their borders. In this paper we propose a new extended version

of the zippering algorithm that enables the user to control the resulting mesh by introducing quality criteria

in the selection of redundant data, and allows to zip together meshes with different granularity by an ad hoc

reﬁnement algorithm.

1 INTRODUCTION AND

PREVIOUS WORK

In recent years, the technology for digitizing real

3D objects has greatly improved and became more

accessible to the general audience. While only

ten years ago the acquisition of the Michelangelo’s

David (Pereira et al., 2000) required 22 people for 30

days and the prototypical device sampled 14k points

per second, nowadays it is possible to acquire a sim-

ilar device for less than 3000$ (NextEngine, 2010).

However, notwithstanding the impressive improve-

ment and diffusion of the hardware, the 3D scanning

software pipeline is substantially unchanged: once the

single range maps have been acquired with the device,

they must be aligned in the same reference system,

then merged in a single triangle mesh. After these

steps others may follow for including colors and/or

for optimizing the resulting mesh for rendering. ai

Over the years each and every step has been reﬁned

in several regards, and nowadays we can safely state

that the 3D acquisition pipeline is a stable process.

Nonetheless, further improvements still can be done

for example in terms of computation time, which is

what we do in this work, focusing on the process of

merging aligned range maps.

A range map is an image where each pixel stores a

depth value, which means that information contained

in a range map is a set of points in 3D space. Given

the regular distribution of the samples in the image

space, it is possible to triangulate them to obtain a

triangle mesh for each range map.

An early mesh merging approach, called zipper-

ing (Turk and Levoy, 1994), consists in stitching to-

gether the pairs of triangulations that overlap in 3D

space by eliminating the redundant faces in the over-

lapping regions and then adjusting the mesh connec-

tivity locally. Other approaches work by triangu-

lating union of the point sets, like the Ball Pivot-

ing (Bernardini et al., 1999), which consists of rolling

an imaginary ball on the point sets and creating a tri-

angle for each triplet of points supporting the ball.

This approach is strictly connected to the idea of α-

shapes (Edelsbrunner and M

ucke, 1994), which may

be thought as a ball pivoting where the ball may ap-

pear simultaneously everywhere outside the scanned

volume. In other approaches, like in (Duan and Qin,

2003), active contours are used to deform a mesh to

ﬁt the sample points. Note that in these cases the ver-

tices of the ﬁnal mesh do not coincide with the initial

samples. In fact, the reconstruction of the ﬁnal repre-

sentation is also a way to ﬁlter the input data to reduce

noise and discard outliers.

Imperfections and noise produced by the scanning

devices is one of the reasons for the success of vol-

umetric methods, which convert the range maps in

a volumetric domain (a discrete distance ﬁeld), well

suited for ﬁltering and merging operations. The Space

Carving proposed in (Curless, 1999) uses range maps

and line of sight of the scanner to determine a con-

ﬁguration of the empty voxels consistent with all the

range images. Many of the improvements to volu-

104

Marras S., Ganovelli F., Cignoni P., Scateni R. and Scopigno R. (2010).

CONTROLLED AND ADAPTIVE MESH ZIPPERING.

In Proceedings of the International Conference on Computer Graphics Theory and Applications, pages 104-109

DOI: 10.5220/0002834301040109

 SciTePress

metric methods consist of enhanced methods for es-

timating distances and normals of the surface. The

method proposed in (Hoppe et al., 1992) uses local

estimation of tangent planes to obtain a signed dis-

tance function. More recent approaches uses MLS

local approximations of the surface to address con-

tinuity of the distance function (Alexa et al., 2001;

Shen et al., 2005) which may be then visualized by

sampling the isosurface with points, using contour-

ing techniques (Fiorin et al., 2007) to build a poly-

gon mesh or ray tracing it at rendering time (Guen-

nebaud and Gross, 2007). A quadratic local approx-

imation scheme has been combined with a hierarchi-

cal space subdivision that allows the reconstructions

of the surface for large number of points in (Ohtake

et al., 2003). In the same ﬂavor, the Poisson Surface

Reconstruction algorithm (Kazhdan et al., 2006) for-

mulates the problem of deﬁning the surface from a set

of point as a Poisson problem, for which a least square

solution can be efﬁciently found at different scales.

The revisitation of the mesh zippering as a mesh

merging algorithm is mainly motivated by the fact

that, thanks to the improvement of both the soft-

ware and the hardware involved in the 3D scanning

pipeline, the quality of acquisition and range maps

alignment may allow to zip them together and to ob-

tain the same result as with more costly and sophisti-

cated methods.

2 ALGORITHM OVERVIEW

Our zippering algorithm consists of the same steps

as the original version presented in (Turk and Levoy,

1994), that we summarizes in the following. Given

two meshes A and B that partially overlap, the zipper-

ing algorithm proceeds in three phases:

• Border Erosion. Remove faces from the border

of the patches to minimize data redundancy.

• Clip a patch against the other. The border of

one of the two range maps is projected on the

other range map, the faces intersected by projec-

tion of A’s border are retriangulated in order to

create a new consistent connectivity.

• Cleaning. Improve the quality of the mesh in the

region when retriangulation occurred.

These phases are revisited to extend the zipper-

ing to support a user-deﬁned criterion to eliminate the

data redundancy and to robustly support the zippering

of patches with very different resolution.

Figure 1: False Positive.

2.1 Border Erosion

In the original zippering algorithm (Turk and Levoy,

1994) a triangular face is said to be redundant if its 3

vertices project on the surface of the other patch. As

it is shown in Figure 1 this process may easily create

holes of roughly the size of the face, that will be even-

tually triangulated after the zippering process. How-

ever there are situations in which we cannot make the

assumption that range maps to be zippered are simi-

lar in terms of size and number of polygons, for ex-

ample because more than one device is used to scan

the surface and the two produce range maps with dif-

ferent granularity. This is quite common in scanning

Cultural Heritage artifacts where there are portions of

the surface that cannot be accessed with the device

used and are subsequently covered with a different

one (Dellepiane et al., 2009).

Therefore we compute the distance between a face

of a patch and the other patch by using a uniform sam-

pling of the face, in order to guarantee a bounded size

of the holes that we may create. We say that a point

projects on the patch if it is closer than a given thresh-

old to the patch and the closest point is not on a border

edge (see Figure 2). Our algorithm classiﬁes a face of

patch A as redundant if all the samples project on the

patch B (and vice versa).

The meaning of eliminating redundant faces is to

redeﬁne the border of the patches, in other terms to

establish a frontier to divide the region where faces

of the mesh A are taken as valid data from the re-

gion where faces of the mesh B are taken. Figure 3

shows three different frontiers for the same pair of

range maps. In the original algorithm a single patch

is chosen as the one containing redundant information

and therefore only its faces are possibly redundant.

Conversely, our algorithm chooses to test redundant

faces on the base of a quality value that we may use,

for example, to preserve faces with lower estimated

acquisition error, or with a better aspect ratio.

Figure 4 sketches the erosion algorithm. The

queue Q stores the faces on the border of the two

patches in ascending order of quality; the face with

lowest quality will be the ﬁrst one of the queue. Start-

CONTROLLED AND ADAPTIVE MESH ZIPPERING

105

Figure 2: Three points and a patch A: distance d

between

and A is greater than a given threshold ε, so P

does not

project on A; distance d

between P

and A is lower than

ε, but the closest point C

is on a border edge of A, so also

does not project on A; ﬁnally, P

project on A, since its

distance from A is lower than ε and closest point does not

lie on border of A.

Figure 3: Two patches (a), labeled as A and B, and possible

frontiers between them; the frontier can be made of border

faces from A (b) or B (c), or it can be mixed with part of

border from A and part from B (d).

ing from the ﬁrst face in the queue, we check all faces,

testing redundancy. Each face is tested once, and then

it is removed from the queue; if the face is redundant,

then it will be also removed from the original mesh,

and its neighbors will be added to Q. The process

stops when Q is empty, and all the faces involved in

the process have been tested.

2.2 Clipping

At this point, the redundant faces have been removed

from A and B and we are in a situation where there is

an overlap between the two meshes so that every face

on the border of a patch is only partially overlapping

the other patch.

Our clipping algorithm consist of two steps:

1. reﬁne the faces on the border of the patch A until

no border edge projects on more than one face of

2. remove from each face of B the part covered by a

Erosion ( Patch A, patch B){

Q = BorderOf (A) + BorderOf (B) ;

while ( ! queue . empty ( ) ) {

Face f = Q. pop ( ) ;

i f ( Redundant ( f , OtherPatch ( f ) ) ){

RemoveFromThePatch ( f ) ;

queue += Adjacents ( f ) ;

}

Figure 4: The erosion algorithm selects the lowest priority

face until there is redundancy of data.

projection and retriangulate the remain.

2.2.1 Reﬁnement

he ﬁrst step if carried out as follows. We keep a queue

of faces of A to be processed and initialize it with

the border faces of A. Then the following steps are

applied until the queue is empty.

Remove a face F

from B

, project its two border

vertices, named v

and v

, on the surface of B. Let F

and F

be the faces of B where projections of v

and

lie, and let e

the border edge between v

and v

Then one of the followings holds:

• F

and F

are the same face, in this case, the pro-

jection of e

lies completely inside the face, we

associate the face F

with F

(see Figure 5.(a)).

• F

is adjacent to F

, that is, they share an edge;

we name this edge e

, in this case we create a ver-

tex on the edge e

positioned at the closest point

of e

to e

and replace the face F

with two faces

as shown in Figure 5.(b), which are inserted in B

• F

is not adjacent to F

, in this case we simply

split the face F

along the middle point of the bor-

der edge and insert the resulting faces in B

(see

Figure 5.(c).

• One of the two vertices does not project on B

(see Figure 6.(a)), in this case we simply consider

the non projecting vertex, say it is v

as project-

ing in an ideal face of patch B passing through v

and process the faces as explained in the previous

cases.

• None of the vertices project, in which case there

is no action to take (see Figure 6.(b)).

In other terms, we reﬁne the faces until the ﬁrst case is

veriﬁed (see Figure 5.(c)). Note that the last two cases

always happen when only a portion of one patch over-

laps the others, while may not be encountered when

using a patch to close a hole.

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

106

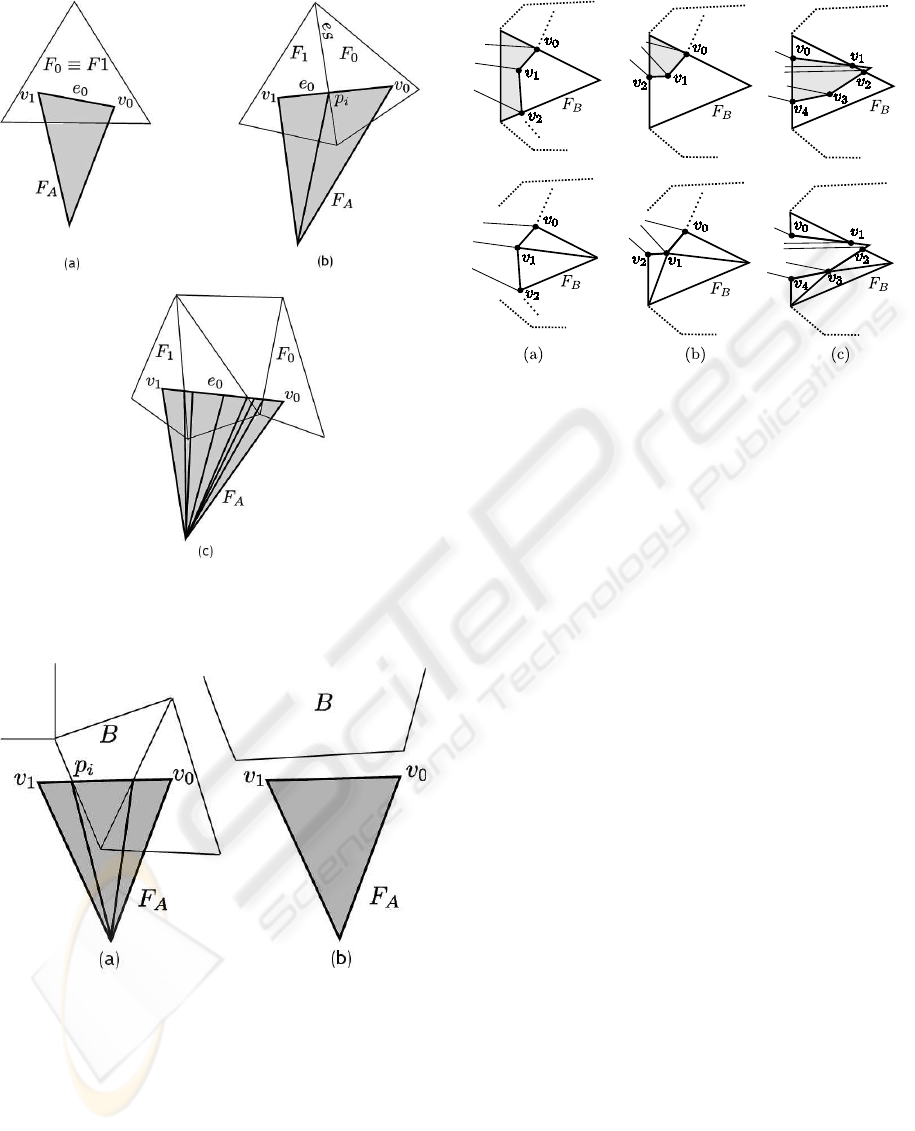
Figure 5: (a) projection of both vertices lie in one face; (b)

in two adjacent faces. (c) projections lie on non adjacent

faces: the border face is recursively split.

Figure 6: Two additional case: vertex v

is not projectable

on mesh, so edge is split on point p

, then only segment

from v

to p

is projected on B; both v

and v

are not pro-

jectable, so F

will not be modiﬁed.

2.2.2 Removal and Retriangulation

At this point each of the projecting faces of A will

be associated with a face of B. What we need to do

is to decompose each face of B in a part clipped by

the projection of the faces of A and a part to be retri-

angulated accordingly to such projections. As shown

Figure 7: Examples of face clipping. The polygon shaded

in gray is to be removed, the rest of face F

will be retrian-

gulated.

in Figure 7 for each face F

to clip we will have one

or more polylines with ending vertices exactly on the

edges of F

, which allow to separate the face in non-

clipped and clipped part. Then we only need to dis-

card the clipped parts and to retriangulate the remain-

ing polygon. Note that in rare situations we can also

have more than one remaining polygon for the same

face (see Figure 7.(c)).

2.3 Cleaning

The quality of the faces is an important part of any

reconstruction techniques. In this sense the zippering

bears a clear disadvantage since it uses a constrained

triangulation. On the other hand, we know exactly the

region of the resulting mesh where the quality of the

faces tends to be poor and may selectively ﬁlter those

parts. Furthermore, we know that the poorly shaped

faces are mostly the result of almost planar subdivi-

sion (during the reﬁnement step) or planar retriangu-

lations (the ﬁnal part of clipping).

3 EXPERIMENTAL RESULTS

In this section, we present some results of the exper-

iments conducted. For each result we also gave in-

formation about time consumed by each stage of the

algorithm. All of the experiments were performed on

a Inter Quad-Core Q9550 2.83GHz equipped with a

NVidia GeForce GTX 260 and 4,00 GB of on-board

memory. Our algorithm has been developed as a plu-

CONTROLLED AND ADAPTIVE MESH ZIPPERING

107

Table 1: Result table for experiment shown in Figure 9.

Criteria Erosion Clipping Cleaning

Preserving model’s face 938 ms 1018 ms 79 ms

Preserving patch’s face 1016 ms 4454 ms 89 ms

Using distance from border 962 ms 1050 ms 90 ms

Figure 8: Test case. A hole in a dense mesh (left) is cov-

ered with with a quad (center) and the algorithm produces a

conformal mesh.

gin for the MeshLab system (Cignoni et al., 2008).

Figure 9 shows a model of a car with a large missing

part and the patch that covers the missing part (top

row). We applied our algorithm with three different

criteria: by preserving the faces of the model, by pre-

serving the faces of the patch and by weighting the

faces on the base of their distance from the border,

so obtaining a clipping frontier in the middle of the

previous two. Table 1 reports the timing for the three

cases.

The most interesting experiment is the compari-

son with the Poisson Surface Reconstruction Algo-

rithm (Kazhdan et al., 2006) to merge two range maps

with 2.5M triangles each. The range maps, obtained

with a Breukmann Smartscan laser scanner1 (Breuck-

mann, 2010), are very dense (100 samples per mil-

limeter) and very well aligned. Figure 10 shows two

range maps merged using PSR (left) and the result or

our zippering algorithm (right). The bottom of the ﬁg-

ure shows the Hausdorff distance between the two re-

sults mapped as false color on the mesh. As expected,

the result is essentially the same and the sewing re-

gions are not noticeable. However, our zippering al-

gorithm took 1m27s seconds to complete against the

6m16s of the Poisson Surface Reconstruction. Note

that the PSR is done with the original source code pro-

vided by the authors and in the same hardware setup.

4 CONCLUSIONS

We presented an improved version of the zipper-

ing algorithm for merging meshes which extends the

original version by enabling enhanced control over

the redundancy of data and supporting merging of

meshes with very different granularity. In the exam-

ples above, we presented results of merging of two

Figure 9: A large hole on the surface of a mesh and zip-

pering with three different criteria: faces from mesh are

preserved, then faces from patch are preserved and, ﬁnally,

faces are weighted using their distance from border.

different mesh, but the procedure can be easily ex-

tended in order to manage more than two meshes,

e.g. two or more patches covering a single hole, or

two or more range maps partially overlapping. Our

experiments shown that with modern range scanners

and thanks to the signiﬁcant improvements made to

the scanning pipeline since the dawn of 3D scanning,

mesh zippering is back as a viable and efﬁcient solu-

tion to merging.

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

108

Figure 10: Poisson reconstruction, on the left, and zip-

perend range maps on the right. The bottom of the ﬁgure

shows Hausdorff distance between the two results mapped

to a ramp between red (0m) and blue(0.001m).

REFERENCES

Alexa, M., Behr, J., Cohen-Or, D., Fleishman, S., Levin, D.,

and Silva, C. T. (2001). Point set surfaces. In VIS ’01:

Proceedings of the conference on Visualization ’01,

pages 21–28, Washington, DC, USA. IEEE Computer

Society.

Bernardini, F., Mittleman, J., Rushmeier, H., Silva, C., and

Taubin, G. (1999). The ball-pivoting algorithm for

surface reconstruction. IEEE Transactions on Visual-

ization and Computer Graphics, 5:349–359.

Breuckmann (2010). Breuckmann smartscan.

http://

www.breuckmann.com

Cignoni, P., Callieri, M., Corsini, M., Dellepiane, M.,

Ganovelli, F., and Ranzuglia, G. (2008). MeshLab: an

Open-Source Mesh Processing Tool. In Sixth Euro-

graphics Italian Chapter Conference, pages 129–136.

Curless, B. (1999). From range scans to 3D models. Com-

puter Graphics, 33(4):38–41.

Dellepiane, M., Venturi, A., and Scopigno, R. (2009). Im-

age guided reconstruction of un-sampled data: a co-

herent ﬁlling for uncomplete cultural heritage mod-

els. In IEEE Workshop on eHeritage and Digital Art

Preservation, page In press. IEEE.

Duan, Y. and Qin, H. (2003). 2.5 d active contour for sur-

face reconstruction. Proceedings of the Eighth Inter-

national Workshop on Vision, Modeling, and Visual-

ization (VMV 2003), page 431439.

Edelsbrunner, H. and M

ucke, E. P. (1994). Three-

Dimensional Alpha Shapes. ACM Transactions on

Graphics, 13:43–72.

Fiorin, V., Cignoni, P., and Scopigno, R. (2007). Out-

of-core MLS reconstruction. In Proc. of he

Ninth IASTED International Conference on Computer

Graphics and Imaging (CGIM), pages 27–34.

Guennebaud, G. and Gross, M. (2007). Algebraic point set

surfaces. ACM Transactions on Graphics, 26:23.

Hoppe, H., DeRose, T., Duchamp, T., McDonald, J., and

Stuelzle, W. (1992). Surface reconstruction from un-

organized points. In ACM Computer Graphics Proc.,

Annual Conference Series, (SIGGRAPH 92), pages

71–78.

Kazhdan, M., Bolitho, M., and Hoppe, H. (2006). Pois-

son surface reconstruction. Proceedings of the fourth

Eurographics symposium on Geometry processing,

page 70.

NextEngine (2010). Nextengine laser scanners.

http://

www.nextengine.com/

Ohtake, Y., Belyaev, A., Alexa, M., Turk, G., and Seidel,

H.-P. (2003). Multi-level partition of unity implicits.

ACM Transactions on Graphics, 22:463–470.

Pereira, M. G., Anderson, S., Davis, J., Ginsberg, J., Shade,

J., and Fulk, D. (2000). The Digital Michelangelo

Project: 3D Scanning of Large Statues. Proc. ACM

SIGGRAPH Conf., pp:131–144.

Shen, C., O’Brien, J. F., and Shewchuk, J. R. (2005). In-

terpolating and approximating implicit surfaces from

polygon soup. ACM SIGGRAPH 2005 Courses on -

SIGGRAPH ’05, page 204.

Turk, G. and Levoy, M. (1994). Zippered polygon

meshes from range images. ACM Computer Graph-

ics, 28:311–318.

CONTROLLED AND ADAPTIVE MESH ZIPPERING

109