FACIAL POSE ESTIMATION USING ACTIVE APPEARANCE

MODELS AND A GENERIC FACE MODEL

Thorsten Gernoth, Katerina Alonso Martínez, André Gooßen and Rolf-Rainer Grigat

Vision Systems E-2, Hamburg University of Technology, Harburger Schloßstr. 20, 21079 Hamburg, Germany

Keywords:

Pose estimation, Active appearance model, Infrared imaging, Face recognition.

Abstract:

The complexity in face recognition emerges from the variability of the appearance of human faces. While

the identity is preserved, the appearance of a face may change due to factors such as illumination, facial pose

or facial expression. Reliable biometric identiﬁcation relies on an appropriate response to these factors. In

this paper we address the estimation of the facial pose as a ﬁrst step to deal with pose changes. We present a

method for pose estimation from two-dimensional images captured under active infrared illumination using a

statistical model of facial appearance. An active appearance model is ﬁtted to the target image to ﬁnd facial

features. We formulate the ﬁtting algorithm using a smooth warp function, namely thin plate splines. The

presented algorithm requires only a coarse and generic three-dimensional model of the face to estimate the

pose from the detected features locations. The desired ﬁeld of application requires the algorithm to work

with many diﬀerent faces, including faces of subjects not seen during the training stage. A special focus is

therefore on the evaluation of the generalization performance of the algorithm which is one weakness of the

classic active appearance model algorithm.

1 INTRODUCTION

In the modern society there is a high demand to au-

tomatically and reliably determine or verify the iden-

tity of a person. For example, to control entry to re-

stricted access areas. Using biometric data to iden-

tify a target person has some well known concep-

tual advantages, such as the identiﬁcation procedure

is immutable bound to the person which should be

identiﬁed. Using facial images as a biometric charac-

teristic has gained much attention and commercially

available face recognition systems exist (Zhao et al.,

2003, Phillips et al., 2007). However unconstrained

environments with variable ambient illumination and

changes of head pose are still challenging for many

face recognition systems.

The appearance of a face can vary drastically if the

intensity or the direction of the light source changes.

This problem can be overcome by employing active

imaging techniques to capture face images under in-

variant illumination conditions. In this work we use

active near-infrared (NIR) illumination (Gernoth and

Grigat, 2010). Possible surrounding light in the visi-

ble spectrum is ﬁltered out.

Another beneﬁt of active near-infrared illumina-

tion is the bright pupil eﬀect which can be employed

to assist eye detection. Pupils appear as unnaturally

Figure 1: The bright pupil eﬀect perceivable under active

near-infrared illumination.

bright spots when an active near-infrared radiation

source is mounted close to the camera axis (Figure 1).

We use image processing to detect these bright spots

in the images and thus can reliable detect the eyes

(Zhao and Grigat, 2006).

Challenging for face recognition systems are also

changes of head pose. Appearance-based face recog-

nition systems use the texture of faces in the form of

two-dimensional frontal images to identify a target

person. But faces are three-dimensional objects and

due to head pose changes, their appearance in images

can change signiﬁcantly.

There are three diﬀerent main strategies to over-

499

Gernoth T., Alonso Martínez K., Gooßen A. and Grigat R. (2010).

FACIAL POSE ESTIMATION USING ACTIVE APPEARANCE MODELS AND A GENERIC FACE MODEL.

In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 499-506

DOI: 10.5220/0002835604990506

 SciTePress

come this problem in appearance-based approaches

for face recognition. The ﬁrst is to use features which

are invariant to these deformations, e. g. invariant to

changes of the facial pose relative to the camera. An-

other strategy is to use or synthetically generate a

large and representative training set. A third approach

is to separate the factors which code the identity of a

person from other sources of variation, such as pose

changes. This is addressed in this paper. The pos-

ture of the head in-front of the camera is estimated

from monocular images. The additional pose infor-

mation may be utilized to register the facial images

very precise and thereby make it possible to perform

face recognition using a pose normalized representa-

tion of faces.

A survey of head pose estimation in computer

vision was recently published by Murphy-Chutorian

and Trivedi, 2009. We use active appearance models

(AAM) to detect facial features in the images. Sub-

sequently, the head pose is determined from a sub-

set of the localized facial features using an analyt-

ical algorithm (DeMenthon and Davis, 1995, Mar-

tins and Batista, 2008). The algorithm can esti-

mate the pose from a single image using four or

more non-coplanar facial features positions and their

known relative geometry. Using three-dimensional

model points from the generic Candide-3 face model

(Ahlberg, 2001, Dornaika and Ahlberg, 2006) and

their image correspondences estimated using the ac-

tive appearance model, the posture of the head in-

front of the camera can be estimated.

Active appearance models are a common ap-

proach to build parametric statistical models of fa-

cial appearance (Cootes et al., 2001, Stegmann et al.,

2000). The desired ﬁeld of application requires the al-

gorithm to work with many diﬀerent faces, including

faces not seen during the training stage (Gross et al.,

2005). We use simultaneous optimization of pose and

texture parameters and formulate the ﬁtting algorithm

using a smooth warping function (Bookstein, 1989).

The thin plate spline warping function is parametrized

eﬃciently to achieve some computational advantages.

A special focus is on the evaluation of the generaliza-

tion performance of the model ﬁtting algorithm.

In Section 2 we introduce statistical models of fa-

cial appearance. Section 3 describes the smooth warp-

ing function. The pose estimation algorithm is ex-

plained in Section 4. With experimental results and

discussion in Section 5, we conclude in Section 6.

2 STATISTICAL MODELS OF

FACIAL APPEARANCE

We parametrize a dense representation of facial ap-

pearance using separate linear models for shape and

texture (Matthews and Baker, 2004). The shape

and texture parameters of the models are statistically

learned from a training set.

2.1 Facial Model

Shape information is represented by an ordered set

of l landmarks x

, i = 1 . . . l. These landmarks de-

scribe the planar facial shape of an individual in a

digital image. The landmarks are generally placed

on the boundary of prominent face components (Fig-

ure 2a). The two-dimensional landmark coordinates

are arranged in a shape matrix (Matthews et al., 2007)

s =



. . . x



, s ∈ R

l×2

. (1)

Active appearance models express an instance s

of a particular shape as mean shape s

and a linear

combination of n eigenshapes s

, i.e.

= s

i=1

. (2)

The coeﬃcients p

constitute the shape parameter

vector p =



, . . . , p



. The mean shape s

and shape

variations s

are statistically learned using a training

set of annotated images (Figure 2a). Since reliable

pupil positions are available (Zhao and Grigat, 2006),

the training images can be aligned with respect to the

pupils in a common coordinate system I ⊂ R

us-

ing a rigid transformation. The images are rotated,

scaled and translated using a two-dimensional simi-

larity transform such that all the pupils fall in the same

position (Figure 2b). The mean shape s

and basis of

shape variations s

are obtained by applying princi-

pal component analysis (PCA) on the shapes of the

aligned training images (Cootes et al., 2001).

The texture part of the appearance is also modeled

using an aﬃne linear model of variation. Texture is

deﬁned as the intensities of a face at a discrete set A

of positions x in a shape-normalized space A ⊂ R

The texture of a face is vectorized by raster-scanning

it into a vector. Similar to the shape, λ =



, . . . , λ



denotes a vector of texture parameters describing a

texture instance

= a

i=1

. (3)

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

500

(a) Annotated image (b) Aligned shapes

Figure 2: Shapes of annotated images aligned with respect

to pupil positions.

(a) a

(b) a

Figure 3: The mean texture a

and the ﬁrst two basis of

texture variations a

The texture at position x ∈ A

of a

is a function

of the domain A, with

: A → R; x 7→ a

(x). (4)

To create a texture model, all the aligned training

images are warped into the shape-normalized space.

The shape-normalized space is given by the mean

shape s

of the shape model. A smooth warping func-

tion that maps one image to another by relating two

sets of landmarks is used as described in Section 3.

contains positions that lie inside the mean shape

. PCA is applied on the training textures to obtain

the mean texture a

and basis of texture variations a

Photometric variations of the texture a

are mod-

eled separately by a global texture transformation

(x)) = (u

+ 1)a

(x)+u

(Baker et al., 2003). The

intensities of the texture vector a

are scaled by a

global gain factor (u

+ 1) and biased by u

To simplify the notation, the parameters describ-

ing shape, texture and photometric variations are

combined into the single parameter vector

q =





. (5)

2.2 Model Fitting

The parameters of the generative model described in

Section 2.1 need to be estimated to ﬁt the model to a

target image. The target image can be aligned to the

common coordinate system with respect to the pupils

(Section 2.1). The target image is regarded as a con-

tinuous function of the domain I:

I : I → R; x

7→ I(x

). (6)

Fitting the model to an image is generally done by

minimizing some error measure between the modeled

texture and the target image. The error at the position

x ∈ A

between the generated texture and the target

image is

e(x, q) = a

(x) − T

(I(W(x, p))). (7)

W(x, p) is a non-linear warping function that maps po-

sitions x ∈ A of the model to positions x

∈ I of the

target image. The warping function is parametrized

by the shape parameters p as described in Section 3.

Typically the sum-of-squared error of all positions

x is minimized to ﬁnd the parameters q, such that

argmin

x∈A



e(x, q)



. (8)

This is a non-linear optimization problem. Gen-

eral optimization techniques can be used to ﬁnd a so-

lution. Commonly used is an iterative Gauß-Newton

style algorithm (Matthews and Baker, 2004). We as-

sume a current estimate of q and solve for incremental

updates ∆q in each step. The update can be combined

with the previous estimate in several ways (Matthews

and Baker, 2004). The simplest update is the linear

additive increment q ← q + ∆q. The following ex-

pression is minimized with respect to ∆q:

argmin

∆q

x∈A



e(x, q + ∆q)



. (9)

Performing a ﬁrst-order Taylor expansion of the

residual e(x, q + ∆q) around q yields:

e(x, q + ∆q) ≈ e(x, q) +

∂e(x, q)

∂q

∆q (10)

≈ e(x, q) +

∂e(x, q)

∂p

∆ p+ (11)

∂e(x, q)

∂u

∆u +

∂e(x, q)

∂λ

∆λ.

The Gauß-Newton algorithm uses the update

∆q = −H

−1

x∈A

e(x, q)

∂e(x, q)

∂q

(12)

with

H =

x∈A

∂e(x, q)

∂q

∂e(x, q)

∂q

. (13)

FACIAL POSE ESTIMATION USING ACTIVE APPEARANCE MODELS AND A GENERIC FACE MODEL

501

Solving for ∆q and using a Gauß-Newton step to

optimize Eq. (9) involves computing an approxima-

tion of the Hessian matrix (Eq. (13)) and its inverse in

each iteration. Assuming a constant Hessian matrix

results in signiﬁcant computational savings (Amberg

et al., 2009, Cootes et al., 2001).

Matthews and Baker, 2004 showed that the lin-

ear additive increment is not the only parameter up-

date strategy. They introduced compositional up-

date strategies which permit overall cheaper algo-

rithms for person-speciﬁc active appearance mod-

els. Their simultaneous inverse compositional algo-

rithm for person-independent active appearance mod-

els (Gross et al., 2005) is however not as computa-

tionally eﬃcient.

3 THIN PLATE SPLINE WARP

A warp function maps positions of one image to posi-

tions of another image by relating two sets of land-

marks. The most common warp functions are the

piecewise aﬃne warp (Glasbey and Mardia, 1998)

and the thin plate spline (TPS) warp (Bookstein,

1989). The aﬃne warp function has the advantage of

being simple and linear in a local region. But although

it gives a continuous deformation, it is not smooth.

Thin plate spline warping as an alternative produces a

smoothly warped image. However, it is more expen-

sive to calculate and non-linear due to the interpolat-

ing function used. In this paper we focus on the thin

plate spline warp.

In the case of our active appearance model, the

warp maps the positions x from the shape-normalized

space A to positions x

∈ I of the target image. The

transformation is such that the landmarks x

, i = 1 . . . l

are mapped to corresponding landmarks x

, i = 1. . . l

of a shape instance s

in the target image. Since the

landmark positions in the target image depend on the

shape parameters p, we parametrize the warp function

by the shape parameter vector p.

The thin plate spline warp function W : A → I is

vector valued and deﬁned as (Bookstein, 1989,Cootes

and Taylor, 2004):

W(x, p) =







i=1

(

kx − x

)







+ c + Cx (14)

= W(p)

|{z}

2×(l+3)

· k(x)

|{z}

(l+3)×1

, (15)

with

W( p) =

. . . w

c C

, (16)

k(x) =

U(r

(x)) . . . U(r

(x)) 1 x

, (17)

where r

(x) = kx − x

k is the Euclidean distance be-

tween a position x and landmark x

of the mean

shape s

. U(r) is the TPS interpolating function (e.g.

U(r) = r

logr

with U(0) = 0) that makes the warp

function non-linear.

W( p) contains the warp weights. The weights c, C

represent the aﬃne part of the mapping in Eq. (14).

The warp weights are deﬁned by the sets of source

and destination landmarks to satisfy the constraints

W(x

, p) = x

∀ i ∈ {1. . . l} and to minimize the bending

energy. Combining all constraints yields in a linear

system (Bookstein, 1989):

K P

W( p)

= L W( p)

(18)

where K is a l × l matrix and K

i j

= U



− x



, the

i’th row of the l × 3 matrix P is



1 x



, O is a 3 × 3

matrix of zeros and o is a 3 × 2 matrix of zeros. If L

is non-singular the warp weights are given by

W( p) =



−1



(19)

with

B =







1 0 · · · 0

0 1 · · · 0

0 0 . . . 1

0 0 · · · 0







| {z }

(l+3)×l

. (20)

During model ﬁtting (Section 2.1) we estimate it-

eratively the parameters p of the shape s

that cor-

responds to the shape of the target image. Since

the residual in Eq. (7) is deﬁned within the shape-

normalized space A given by s

, the matrix L de-

pends only on the landmarks x

of the mean shape s

The mean shape does not change for a give training

set. L and its inverse can therefore be precomputed.

Parametrization of the warp function with respect

to p yields another computational advantage. The tex-

ture is deﬁned at a discrete set of positions A

(Sec-

tion 2.1). The residual in Eq. (7) only need to be eval-

uated at these positions. The positions depend on s

and do not change for a give training set. k(x) can

also be precomputed for all x ∈ A

Using Gauß-Newton to minimize Eq. (9) requires

the Jacobian matrix

∂W(x, p)

∂p

of the warp function with

respect to the shape parameters (Eq. (11)):

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

502

∂e(x, q)

∂p

= −

∂T

(I(W(x, p))

∂p

(21)

= −

∂T

(I(W(x, p))

∂W (x, p)

W(x, p)

∂p

(22)

Using the parametrization of the warp function

with respect to p gives the components of the Jaco-

bian matrix as follows:

∂W (x, p)

∂p

= s



−1



k(x). (23)

The Jacobian does not depend on the value of the eval-

uation point p and can be precomputed for all x ∈ A

4 POSE ESTIMATION

The pose of a face in-front of the camera is deﬁned

as its position and orientation relative to a three-

dimensional camera coordinate system. We denote by

a three-dimensional feature point of a face model in

a coordinate system attached to the model. The per-

spective projection of a feature point onto the image

plane of the camera is x

. The pose of a face with

respect to a camera can be deﬁned with a translation

vector t ∈ R

and a rotation matrix R ∈ SO(3):

• The translation vector is the vector from the origin

of the coordinate system attached to the camera to

the origin of the face model: t =





• The rotation matrix is the matrix whose rows are

the unit vectors of the camera coordinate system

expressed in the coordinate system of the face

model: R =

i j k

Under perspective projection with a camera hav-

ing focal length f , x

is related to the corresponding

feature point of the model

as follows:

+ t

. (24)

The equation may be written as in DeMenthon and

Davis, 1995,

(1 + 

) −

, (25)

with i

i, j

j, t

, t

and 

By setting 

= 0, x

equals the scaled orthographic

projection of the face model point

. Scaled ortho-

graphic projection is similar to perspective projection

if the depth of the face is small compared to its dis-

tance to the camera. For the case of ﬁxed 

and as-

suming known projection of the model origin onto the

(a) AAM Landmarks (b) Candide Model

Figure 4: (a) The selected landmarks for pose estimation

and (b) the corresponding Candide-3 model.

image plane, the unknown i, j and t

can be com-

puted from Eq. (25) from at least 4 non-coplanar fea-

ture points (DeMenthon and Davis, 1995,Martins and

Batista, 2008). The third row of the rotation matrix R

can be obtained from the cross product k = i × j. Us-

ing an iterative scheme and estimating 

from k and

of the previous iteration, an approximation of the

pose can be computed.

4.1 Generic Face Model

A three-dimensional model of the face shape is re-

quired to estimate the pose. The Candide-3 model

(Ahlberg, 2001) is used. This general model is used

in its neutral state but adapted in scale for facial pose

estimation of all subjects (Figure 4b).

4.2 Feature Point Selection

As stated above, the algorithm requires at least 4 non-

coplanar feature points to estimate the facial pose.

These points are chosen from the estimated landmark

positioning provided by the AAM. A correspondence

was established between the Candide-3 model points

and the landmarks of the active appearance model.

Since only one generic face model is used, the

landmarks which do not vary much between faces

of diﬀerent subjects are chosen as feature points for

pose estimation. The variability of each landmark was

studied in order to pick the most stable ones. As it can

be seen in Figure 4a, two landmarks from the eye con-

tour and landmarks on the nose are chosen. The nose

tip is used as the origin of the coordinate system of

the face model.

5 EXPERIMENTS

We use the TUNIR database (Zhao et al., 2007) for

all experiments. The database consists of recordings

FACIAL POSE ESTIMATION USING ACTIVE APPEARANCE MODELS AND A GENERIC FACE MODEL

503

Subject

Landmark Distance [pixel]

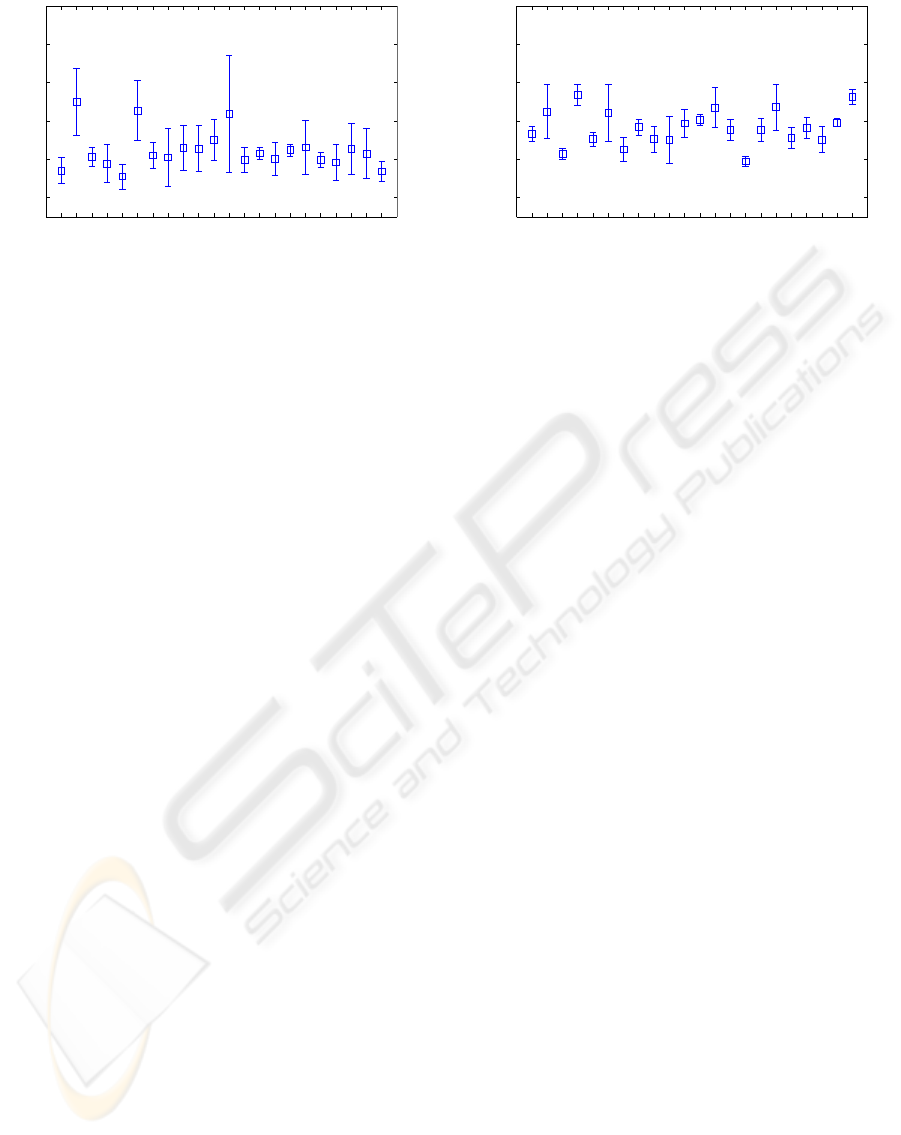
Figure 5: Mean and standard deviation of the distance be-

tween estimated and hand-labeled landmarks used for pose

estimation for each subject (Person-speciﬁc AAM).

of 74 people in a typical access control scenario under

active near-infrared illumination. The subjects move

in-front of the camera and were asked to speak to

recreate a realistic scenario.

5.1 Model Fitting

To evaluate the performance of the AAM ﬁtting al-

gorithm with smooth warp function, 5 images of 22

subjects from the TUNIR database were labeled in a

semi-automatic way with 67 landmarks. Before ﬁt-

ting, the shapes were prepositioned according to the

pupil positions, as described in Section 2.1. A hi-

erarchical approach with two levels was chosen. To

evaluate the ﬁtting ability of the algorithm and for

comparison, an experiment with known subject but

novel image was conducted. Person-speciﬁc active

appearance models were trained for each subject and

evaluated in a leave-one-out cross-validation manner.

90% of shape variance and 95 % of appearance vari-

ance of each training set were retained in the model.

This corresponds to the optimal settings for the ex-

periment with generic active appearance models de-

scribed below. In Figure 5 the mean and standard de-

viation of the distance between the estimated and the

hand-labeled landmarks are shown for each subject.

Only the landmarks which are used for pose estima-

tion contribute to the evaluation of the landmark dis-

tance.

Of more interest for the desired ﬁeld of applica-

tion is the performance with subjects not seen during

training. In a second experiment generic active ap-

pearance models were trained from all but one sub-

ject. All images of the remaining identity were used

to evaluate the performance of the ﬁtting algorithm.

Of interest is again the distance between the estimated

and the hand-labeled landmarks used for pose estima-

tion. This is shown in Figure 6.

As expected, the mean distance between estimated

Subject

Landmark Distance [pixel]

Figure 6: Mean and standard deviation of the distance be-

tween estimated and hand-labeled landmarks used for pose

estimation for each subject (Generic AAM).

and hand-labeled landmarks is lower for person spe-

ciﬁc active appearance models. Nevertheless, the to-

tal mean distance is also just 1.8 pixels for generic ac-

tive appearance models. In many cases the estimated

landmarks ﬁt well the face components but do not

match the hand-labeled landmarks. This is because

the hand-labeled positioning is not necessary the op-

timum one. Data reﬁtting (Gross et al., 2005) could

improve the performance. After a visual inspection of

the estimated landmarks, an error up to 3pixels was

considered as good performance for the application.

5.2 Pose Estimation

To test the accuracy of the pose estimation algo-

rithm quantitatively, we used the three-dimensional

Candide-3 model. Of interest was the quality of

the pose estimation from landmarks perturbed in the

range of what can be expected from the AAM ﬁtting

algorithm. The Candide-3 model was situated in 729

diﬀerent positions. We obtained simulated landmarks

by projecting the three-dimensional model points per-

spectively to an image plane corresponding to the

application scenario. We uniformly perturbed these

landmarks from 1 pixels to 10 pixels and estimated the

pose using the algorithm described in Section 4.

In Figure 7, the mean distance of the true model

points to the model points of the Candide-3 model

with estimated pose for diﬀerent ranges of landmark

perturbation is shown. Figure 7 shows that for a per-

turbation between 3 and 4 pixels, the mean model

point distance is just around 7pixels.

A typical result of pose estimation is shown in Fig-

ure 8. Since the posture of the subjects in-front of the

camera is not known for the test images of the TU-

NIR database, the performance could only be evalu-

ated qualitatively for this database.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

504

0 2 4 6 8 10

Landmark Perturbation [pixel]

Model Point Distance

Figure 7: Mean and standard deviation of the distance be-

tween true model points and model points with estimated

pose for diﬀerent ranges of landmark perturbation.

Figure 8: The estimated pose of a subject of the TUNIR

database.

6 CONCLUSIONS

We presented an approach for facial pose estimation

from two-dimensional images using active appear-

ance models. Only a generic three-dimensional face

model is required for pose estimation. We formulated

the active appearance model ﬁtting algorithm in an

eﬃcient manner with a smooth warp function. Our

experiments show that the ﬁtting accuracy of the al-

gorithm is suﬃcient to estimate the pose from the de-

tected landmark positions. Estimated poses from test

images of the TUNIR database emphasize this result

qualitatively.

ACKNOWLEDGEMENTS

This work is part of the project KabTec – Modulares

integriertes Sicherheitssystem funded by the German

Federal Ministry of Economics and Technology.

REFERENCES

Ahlberg, J. (2001). Candide-3 – an updated parame-

terized face. Technical Report LiTH-ISY-R-2326,

Dept. of Electrical Engineering, Linköping Univer-

sity, Linköping, Sweden.

Amberg, B., Blake, A., and Vetter, T. (2009). On compo-

sitional image alignment, with an application to ac-

tive appearance models. In Proc. IEEE Conference

on Computer Vision and Pattern Recognition (CVPR

2009), pages 1714–1721.

Baker, S., Gross, R., and Matthews, I. (2003). Lucas-

Kanade 20 years on: A unifying framework: Part 3.

Technical Report CMU-RI-TR-03-35, Robotics Insti-

tute, Carnegie Mellon University, Pittsburgh, PA.

Bookstein, F. (1989). Principal warps: thin-plate splines

and the decomposition of deformations. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

11(6):567–585.

Cootes, T., Edwards, G., and Taylor, C. (2001). Active ap-

pearance models. IEEE Transactions on Pattern Anal-

ysis and Machine Intelligence, 23(6):681–685.

Cootes, T. and Taylor, C. (2004). Statistical models of ap-

pearance for computer vision. Technical report, Uni-

versity of Manchester, Manchester, U.K.

DeMenthon, D. F. and Davis, L. S. (1995). Model-based

object pose in 25 lines of code. International Journal

of Computer Vision, 15(1-2):123–141.

Dornaika, F. and Ahlberg, J. (2006). Fitting 3d face mod-

els for tracking and active appearance model training.

Image and Vision Computing, 24(9):1010 – 1024.

Gernoth, T. and Grigat, R.-R. (2010). Camera characteri-

zation for face recognition under active near-infrared

illumination. In Proc. SPIE, volume 7529, page

75290Z.

Glasbey, C. A. and Mardia, K. V. (1998). A review of

image-warping methods. Journal of Applied Statis-

tics, 25(2):155–171.

Gross, R., Matthews, I., and Baker, S. (2005). Generic vs.

person speciﬁc active appearance models. Image and

Vision Computing, 23(1):1080–1093.

Martins, P. and Batista, J. (2008). Monocular head pose

estimation. In Proc. 5th international conference on

Image Analysis and Recognition (ICIAR ’08), pages

357–368.

Matthews, I. and Baker, S. (2004). Active appearance mod-

els revisited. International Journal of Computer Vi-

sion, 60(2):135–164.

Matthews, I., Xiao, J., and Baker, S. (2007). 2d vs. 3d de-

formable face models: Representational power, con-

struction, and real-time ﬁtting. International Journal

of Computer Vision, 75(1):93–113.

Murphy-Chutorian, E. and Trivedi, M. (2009). Head pose

estimation in computer vision: A survey. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

31(4):607–626.

FACIAL POSE ESTIMATION USING ACTIVE APPEARANCE MODELS AND A GENERIC FACE MODEL

505

Phillips, P. J., Scruggs, W. T., O’Toole, A. J., Flynn, P. J.,

Bowyer, K. W., Schott, C. L., and Sharpe, M. (2007).

FRVT 2006 and ICE 2006 Large-Scale Results. Tech-

nical Report NISTIR 7408, National Institute of Stan-

dards and Technology, Gaithersburg, MD.

Stegmann, M. B., Fisker, R., Ersbøll, B. K., Thodberg,

H. H., and Hyldstrup, L. (2000). Active appearance

models: Theory and cases. In Proc. 9th Danish Conf.

Pattern Recognition and Image Analysis, pages 49–

57.

Zhao, S. and Grigat, R.-R. (2006). Robust eye detection

under active infrared illumination. In Proc. 18th In-

ternational Conference on Pattern Recognition (ICPR

2006), pages 481– 484.

Zhao, S., Kricke, R., and Grigat, R.-R. (2007). Tunir: A

multi-modal database for person authentication under

near infrared illumination. In Proc. 6th WSEAS Inter-

national Conference on Signal Processing, Robotics

and Automation (ISPRA 2007), Corfu, Greece.

Zhao, W., Chellappa, R., Phillips, P. J., and Rosenfeld, A.

(2003). Face recognition: A literature survey. ACM

Computing Surveys, 35(4):399–458.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

506