
STRUCTURE FROM MOTION OF LONG VIDEO SEQUENCES
Siyuan Fang and Neill Campbell
Department of Computer Science, University of Bristol, Bristol, U.K.
Keywords:
Camera pose estimation, Sparse 3D structure reconstruction, Bundle adjustment.
Abstract:
In this paper we introduce an approach for “Structure from Motion” from long video sequence. Our approach
starts from an initialization of first several frames and adopts an incremental strategy to allow more frames
to be added into the SFM system. The main contribution lies in that we introduce an update propagation
to modify the entire SFM system to accommodate changes brought by the local bundle adjustment applied
to newly added frames. With this step, our approach gains a significant accuracy improvement at a cost of
relatively small extra computation overhead.
1 INTRODUCTION
This paper presents a structure from motion approach
for long video sequences with fixed intrinsic camera
parameters. The term “Structure from motion” (SFM)
(Hartley and Zisserman, 2004) refers to the process of
automatically recovering camera parameters and re-
constructing the 3D scene structure from recorded 2D
images. It has been a central issue of computer vision
for decades and there are many implemented systems
(2d3, 2000; Digi-lab, 2005). Many applications of
SFM can be found in different fields, such as image-
based rendering , virtual reality and stereo.
Most SFM algorithms are based on point cor-
respondence form different views, from which the
epipolar geometry, e.g., the fundamental matrix for
two-views, can be extracted. A projective reconstruc-
tion of camera parameters can be calculated from the
epipolar geometry, which is then upgraded to a metric
one using the intrinsic camera parameter. Once cam-
eras are recovered, 3D points can be constructed us-
ing the triangulation. Up to this stage, we are given a
very coarse estimate, upon which a further optimiza-
tion is required to minimize the reprojection error. For
normal pinhole cameras, the most common optimiza-
tion approach is the bundle adjustment (Triggs et al.,
1999), which minimizes reprojection errors by simul-
taneously refining the 3D structure and cameras in
a non-linear style. The bundle adjustment requires
an initialization for following iterative adjustments.
Currently, most bundle adjustment algorithms are im-
plemented using the Levenberg-Marquardt method
(Hartley and Zisserman, 2004; Lourakis and Argy-
ros, 2009), which, compared to the traditional Gauss-
Newton method, is faster and less sensitive to poor
initial estimates. However, a good initialization is still
of great importance, because it can provide a faster
convergence for the iteration process, and more cru-
cially, in some cases, it can even determine the suc-
cess of the bundle adjustment.
For long sequences, the reconstruction usually
starts from several reference frames, and an incremen-
tal mechanism is necessary to allow more views to
be added into the current system. As the sequence
length increases, the accumulated error may cause
the initial estimate far away from the real one, and
therefore, provide the bundle adjustment a poor ba-
sis. To solve this problem, one may suggest perform-
ing the the bundle adjustment over all frames so far
handled at each increment step. However, the bun-
dle adjustment is computationally expensive. Accord-
ing to (Shum et al., 1999), the complexity of each it-
eration of bundle adjustment is O(m · n
3
), where m
is the number of 3D points and n is the number of
frames. To improve the efficiency, it is desired to
reduce the number of fames involved. For the in-
cremental SFM system, the local bundle adjustment,
which restricts the refinement to only several frames
around the currently added one, is preferable (Zhang
and Shan, 2003; Mouragnon et al., 2009; Zhang et al.,
2007).
This paper aims to deliver a robust incremental
361
Fang S. and Campbell N. (2010).
STRUCTURE FROM MOTION OF LONG VIDEO SEQUENCES.
In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 361-366
DOI: 10.5220/0002836203610366
Copyright
c
SciTePress

SFM approach, which supplies a good starting point
for global bundle adjustments. In addition, such a in-
cremental system itself is useful in many applications.
Imagining the case that a global bundle adjustment is
not affordable due to the efficiency requirement, an
incremental SFM approach which can provide a re-
sult with almost the same precision is really needed.
The local bundle adjustment is adopted in our ap-
proach for incrementally expanding the current recon-
struction. A problem arising is that the local bundle
adjustment of each expansion step might change the
existing reconstruction. Obviously these changes will
bring extra errors to the previous reconstruction. And
more importantly, with increasing sequence length,
these relatively small changes can be accumulated to
a sufficient amount that invalidate the previous recon-
struction. In this case, the incremental algorithm is
at risk of losing the basis for further expansion. To
alleviate this problem, we adopts an update propaga-
tion method, which modify the entire reconstruction
to cater for changes brought by the local bundle ad-
justment. Compared to the pure local bundle adjust-
ment, our approach is clearly slower due to the extra
expense of the update propagation, but gains a signif-
icant accuracy improvement.
In this paper, we assume the intrinsic parameter of
the camera is known and fixed, i.e., we will not deal
with the self-calibration problem.
The rest of this paper is organized as: Section
2 introduces some math notations used in this paper
and presents an overview of our approach. Section
3 describes how the reconstruction is initialized from
reference frames. Section 4 introduce our incremen-
tal method for reconstruction expansion. Section 5
presents the results. Section 6 concludes this paper.
2 THE FRAMEWORK
We first introduce the math notation used throughout
this paper. Suppose we are given a sequence with n
frames: {I
i
}
n−1
0
. For each I
i
, the corresponding cam-
era is modeled by the intrinsic parameter K, which is
a 3 ×3 up-triangle matrix, (we assume K remains un-
changed across the frame), and the extrinsic param-
eter [R
i
| t
i
], where R
i
is a 3 × 3 orthonormal rota-
tion matrix and t
i
= (tx
i
,ty
i
,tz
i
) is a translation vec-
tor. The projection matrix of such a camera is that:
P = K · [R
i
| t
i
].
To reduce the parameter number, the rotation of
each camera can be described by its Euler angle:
ω
i
= (α
i
, β
i
, γ
i
). In this case, the camera C
i
is parame-
terized by a 6-vector: C
i
= (α
i
, β
i
, γ
i
,tx
i
,ty
i
,tz
i
). The
projection of a 3D points X
j
= [x
i
, y
i
, z
i
]
T
onto a 2D
image by C
i
can be expressed by a non-linear func-
tion Θ such that: Θ(C
i
, X
j
).
For a sequence to be reconstructed, sparse points
are matched consecutively, i.e., I
1
against I
0
, I
2
against I
1
and etc. The point matching is based on cer-
tain feature tracking techniques, (we have tried bother
SIFT (Lowe, 2004) and KLT points (Shi and Tomasi,
1994)). The Random Sample Consensus (RANSAC)
algorithm is used to fit the fundamental matrix that
encapsulates the epipolar constraint. Therefore, the
track of a point can be lost in a given frame for two
reasons: there is no matched point or the match does
not conform to the epipolar constraint. For each track,
a 3D point can be constructed if corresponding cam-
era parameters are known.
If the camera moves slowly, we resample the se-
quence to select some keyframes that have wider
base-lines. In addition, since information contained
in a long track is more reliable than a short one. We
only consider tracks that are not shorter than certain
minimal track length (T ). T is usually set to be 3
keyframes.
The reconstruction process is initialized from first
several frames. Then more frames are added incre-
mentally to expand the current reconstruction. Each
expansion is accomplished by two steps: 1. Firstly,
the local bundle adjustment is performed over several
neighbouring frames around the newly added frames.
2. Then, the update brought by the local bundle ad-
justment is propagated to the entire reconstruction.
After all frames are processed, if the remaining re-
projection error is still large, an optional global bun-
dle adjustment is applied to refine the result. Finally,
Cameras of non-keyframes are calculated based on
the reconstructed 3D points, if the sequence has been
resampled.
3 RECONSTRUCTION
INITIALIZATION
The first (0
th
) frame is always selected as the refer-
ence frame, such that R
0
= I and t
0
= 0. We select
the first s (s ≥ 3) frames to initialize the reconstruc-
tion. The length of s is based on how many tracks
can be seen from both the 0
th
and the i
th
(0 < i < s)
frame. The minimal number of such tracks is set to
30. For each of non-reference initialization frames,
its fundamental matrix against the reference frame F
i
is discovered based on inlier matches. With the intrin-
sic matrix K, the epipolar constraint can be upgraded
from the fundamental matrix to an essential matrix E
i
:
E
i
= K
T
· F
i
· K.
Then, the essential matrix is decomposed into an
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
362

orthonormal matrix corresponding to the rotation ma-
trix and a skew-symmetric matrix corresponding to
the translation vector:
E
i
= [t
i
]
×
R
i
(1)
The decomposition is implemented using the
singlular value decomposition (SVD), which returns
two twisted configurations of R
i
and two reflected
configurations of t
i
, therefore in total four combina-
tions. To remove the ambiguity, these four configura-
tions are tested with a single reconstructed 3D point to
make sure that such a point is in front of both the 0
th
and i
th
camera (Hartley and Zisserman, 2004). Once
the rotation matrix is computed, its corresponding Eu-
ler angle ω
i
can be extracted.
Since translation vectors achieved from the above
process are normal vectors that only parameterizes di-
rections, relative scales have to be discovered. We de-
fine the translation between the 0
th
and 1
st
camera as
a reference scale. The following scale of translation
can be determined using the 3D points triangulated
from the 0
th
and 1
st
camera. Suppose that the x
i j
is
the observed 2D point of the projection from j
th
3D
point onto the i
th
frame, the problem of determining
the scale l is formulated into a linear Least Squares
estimation: A · l = B. Each visible X
j
provides two
linear functions:
((K ·t
i
)
1>
− u
i j
· (K · t
i
)
3>
)
((K ·t
i
)
1>
− v
i j
· (K · t
i
)
2>
)
| {z }
A
j
·l =
u
i j
· (K · R
i
· X
j
)
3>
− (K · R
i
· X
j
)
1>
v
i j
· (K · R
i
· X
j
)
3>
− (K · R
i
· X
j
)
2>
| {z }
B
j
(2)
where ()
i>
denotes the i
th
row of a matrix. The
linear system is solved by SVD.
After all the initialization frames are processed,
tracks falling into this segment are selected to con-
struct the corresponding 3D points using the linear
DLT triangulation (Hartley and Zisserman, 2004).
Then the bundle adjustment is applied to guarantee
an accurate initialization. Suppose that the Euclidean
distance between the observed image and the repro-
jected point from the estimated X
j
and C
i
is denoted
by d(x
i j
, Θ(C
i
, X
j
). Assuming that, so far, we have
been given s frames and m
c
3D points (or tracks). The
goal of the bundle adjustment is to find an optimal
estimation that has the maximal likelihood given the
observed data, in other words, minimizes the sum of
distances between the observed 2D points and the 2D
points predicted by the estimation, specifically:
min
{C
i
}
s−1
1
,{X
j
}
m
c
−1
0
m
c
−1
∑
j=0
s−1
∑
i=1
d(x
i j
, Θ(C
i
, X
j
))
2
(3)
There are in total 6 ∗ (s − 1) + 3 ∗ m
c
parameters
involved in the minimization, as we assume the ref-
erence frame is fixed. It is usually not reliable to
initialize from only first several frames. In practice,
we make use of more frames s
0
, which can be cho-
sen based on the total length of the sequence, say
n
5
.
The reconstruction is extended from s to s
0
using the
expansion strategy presented in the next section.
4 RECONSTRUCTION
EXPANSION
Suppose that frames from I
0
to I
i−1
has been pro-
cessed, so that the corresponding cameras C
0
to C
i−1
are recovered and a set of 3D points are reconstructed.
The new frame I
i
is added into the current SFM sys-
tem. We initialize the camera C
i
using the previously
reconstructed 3D points that are visible in I
i
. Suppose
that there are m
v
such 3D points, the cost function for
calculating C
i
is that:
min
C
i
m
v
−1
∑
j=0
d(x
i j
, Θ(C
i
, X
j
))
2
(4)
For each expansion step, we add into the SFM sys-
tem h new frames. h varies according to how many
3D points can be seen in the newly added frame.
The minimal visible 3D points are usually set to be
m
v
= 30. For the local bundle adjustment, an over-
lapping number o is chosen to set how many previ-
ously recovered cameras are involved in the current
refinement, i.e., the local bundle adjustment is per-
formed over frames {I
i−o
, ..., I
i−1
, ..., I
i+h−1
}. In order
to maintain information from previous reconstruction,
the fixation number f ix is set to prescribe how many
frames starting from I
i−o
should keep unchanged in
the current local bundle adjustment (2 ≤ f ix ≤ o).
3D points that have been refined by the current lo-
cal bundle adjustment can be divided into two groups:
those have been previously reconstructed and can be
seen from frames {I
0
, ..., I
i−o−1
}, which is denoted by
V , and those cannot. For the former, changes brought
by the local bundle adjustment have to be propagated.
For each frame falling in {I
0
, ..., I
i−o−1
}, we check if
there is a 3D point from V is visible in that frame.
If so, we refine the corresponding camera C using 4.
The minimization process takes the current parameter
as the initial guess. An illustration of this process is
presented in Figure 1.
After cameras of all the affected frames haven
been updated, a further reconstruction of all 3D points
that have been involved so far is introduced, such that:
min
{X
j
}
m−1
0
m−1
∑
j=0
i+h−1
∑
i=1
d(x
i j
, Θ(C
i
, X
j
))
2
(5)
STRUCTURE FROM MOTION OF LONG VIDEO SEQUENCES
363

(a) The Crow.Rd sequence
(b) The Office sequence
(c) The Pkway.St sequence
Figure 2: Example frames of testing sequence and visualizations of reconstructed 3D points and cameras.
Ii-o-1
o111
11
Ii-o
Ii-h+1
Ii- 1
Ii-o-2
I0
Ii-o-3
X1
X2
Figure 1: Illustration of the local bundle adjustment and
update propagation: Newly added cameras are denoted by
red dashed lines and camera involved in current local bun-
dle adjustment are denoted by dashed line. Suppose that
the previously constructed 3D points X
1
and X
2
are updated
due to the current local bundle adjustment, X
1
is visible in
I
i−o−3
, I
i−o−2
and I
i−o−1
, X
2
is visible in I
i−o−2
and I
i−o−1
.
Therefore, these cameras have to be updated.
(Steedly and Essa, 2001) proposes an approach in
a similar style to incorporate updates brought by new
frames. However, we are more concerned with the lo-
cal information propagation, rather than achieving a
global minimum for each expansion step. As men-
tioned above, after cameras of affected frames are
solved, we reconstruct 3D points assuming that all
camera parameters are optimized. Compared to the
section-resection framework that alternates between
the process of camera parameters estimation and 3D
reconstruction (Mahamud et al., 2001), this is concep-
tually equivalent to forcing such process to stop at that
moment, otherwise our update propagation will be-
come another global bundle adjustment. Indeed, we
will show in Section 5 that this will not incur a large
precision lost.
5 EXPERIMENTS
Our SFM system is implemented using the C++ pro-
gramming language on the WindowsXP platform.
The experiment is conducted on a desktop PC with In-
Table 1: Statistics of test sequences.
Crow.Rd Pkway.St Office
Frames N 810 227 672
Keyframes N 73 75 112
Tracks (3D pts) N 1712 2020 2784
Projection N 12496 16135 22441
Overlapping (o) N 5 8 5
Fixation ( f ix) N 5 6 5
Initialization (s
0
) N 15 15 22
tel Pentium 2.40 GHz CPU and 1.50GB RAM mem-
ory.
Three video sequences are used as our testing
data. The Crowther Road sequence is captured around
a corner of a living neighborhood of Bristol with
a hand-held camera. The Parkway street sequence
captures a business street of Bristol with a camera
mounted on a moving vehicle and The Office se-
quence films scenes of our office with a hand-held
camera. All these three sequences are not closed.
Statistics of these three sequence are presented in Ta-
ble 1. Reconstructions are visualized (using our 3D
visualizer) in Figure 2 together with some example
input frames.
To show the strength of our incremental approach
(local bundle adjustment plus update propagation),
we compare our result with those of pure local bun-
dle adjustment and global bundle adjustment. For
simplicity, these three approaches are denoted as
LBA+UP, LBA, and GBA respectively. For compari-
son, we consider two facts, the accuracy and the com-
putation cost, which are used to demonstrate that with
a relatively small expense, our LBA+UP approach is
much more robust than the LBA approach, and some-
times it is even comparable with the GBA approach.
In addition, for showing that our LBA+UP is able to
provide a more solid basis for a final GBA, we also
compare results of two types of GBA, one takes the
traditional LBA result as the initial estimate, and the
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
364
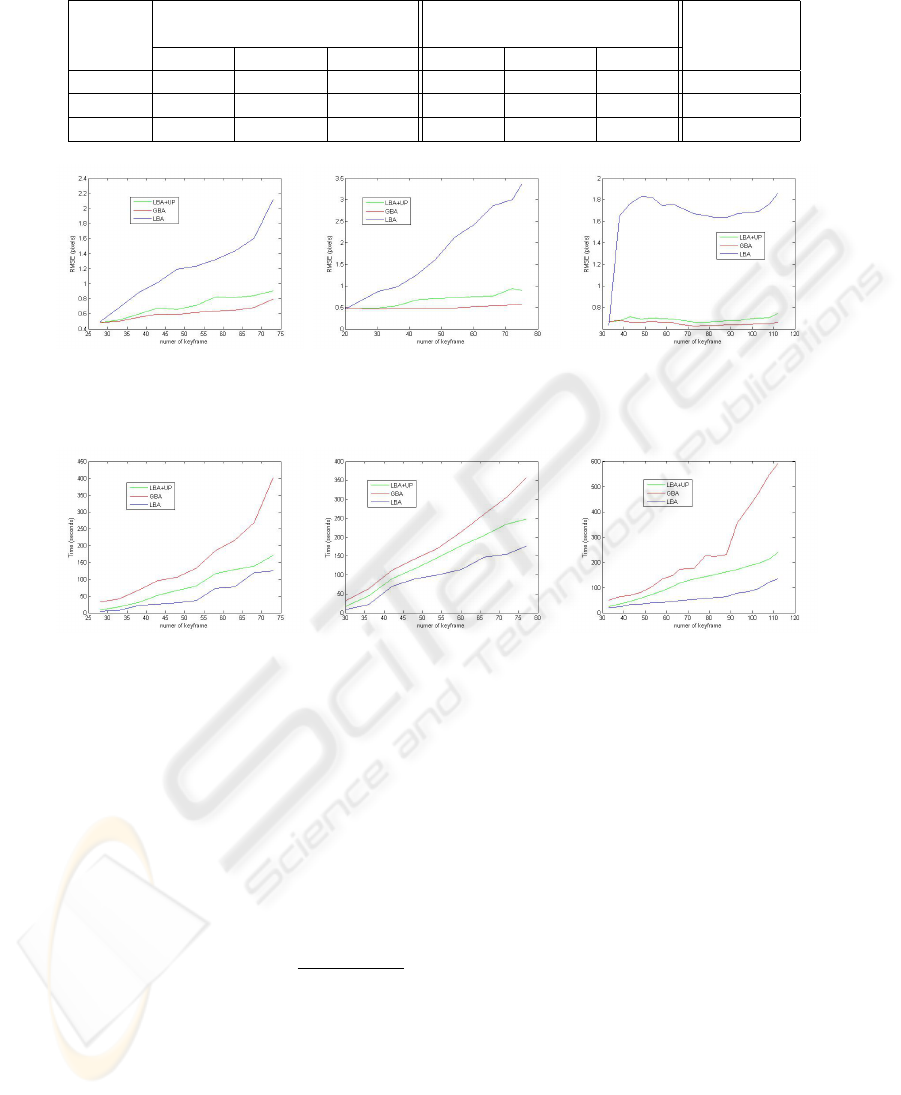
Table 2: Comparison results of different approaches.
RMSE (pixel) Time (Second) RMSE of GBA
based on LBA
LBA LBA+UP GBA LBA LBA+UP GBA
Crow.Rd 2.11884 0.906058 0.794769 124.772 170.519 400.033 1.62013
Pkway.St 3.36435 0.898319 0.568826 176.262 247.37 355.945 1.36299
Office 1.86079 0.745086 0.663738 133.615 238.804 591.199 0.671995
(a) (b) (c)
Figure 3: Visualization of how accuracy varies with the increasing keyframe number. From left to right: the Crow.Rd, the
Pkway St and Office.
(a) (b) (c)
Figure 4: Visualization of how computation cost varies with the increasing keyframe number. From left to right: the Crow.Rd,
the Pkway St and Office.
other takes our LBA+UP result as the initial guess.
For each sequence, experiments are carried out with
the same parameters, such as the overlapping segment
length (o), the fixation number f ix, the initialization
length s
0
, and other arguments like stopping condi-
tions of the bundle adjustment.
Since there is no ground truth available, the re-
projection error is used to measure the accuracy. The
reproejction error is expressed by the Residual Mean
Squared Error (in pixels): RMSE =
∑
d(x
i j
,Θ(C
i
,X
j
))
N
pro j
,
where N
pro j
is the total number of projection. The
computation cost is measured by the time (in sec-
onds). We only record the time related to solving
cameras and 3D points, as the efficiency of feature
tracking is not considered in this paper.
Table 2 presents comparison results, from which
it can be seen that: for long sequences, the perfor-
mance of pure LBA is not reliable, while the accu-
racy of our LBA+UP approach is quite close to the
GBA (here it takes the result of LBA+UP as the ini-
tial guess). Although our LAB+UP would bring some
extra overhead, compared to the GBA, it still saves a
lot of time. Considering the high precision improve-
ment, we would say that it is worth of accepting such
relatively small efficiency lost.
In addition, we also present the RMSE of GBA
that takes the LBA as its initial guess, (the last column
of Table 2). Compared to that based on the LBA+UP
(the third column), we can see that our approach pro-
vides a much better starting point for the GBA.
Figure 3 and 4 visualize how those compari-
son statistics changes with the increase of sequence
length. It is can be observed that with the sequence
extended, the accuracy of LBA drops rapidly and the
computation cost of GBA grows steadily, while our
LBA+UP approach achieves a best tradeoff between
them.
STRUCTURE FROM MOTION OF LONG VIDEO SEQUENCES
365

6 CONCLUDING REMARKS
In this paper we present a new incremental SFM ap-
proach with fixed intrinsic camera parameter. Apart
from the local bundle adjustment carried out for each
expansion step, we introduce an update propagation
step which modify the entire current reconstruction
system to cater for changes brought by the local ad-
justment. Experiments on real data shows our ap-
proach works much better than those with merely lo-
cal bundle adjustment, in that it is more accurate itself
and provides a better initial guess for the global bun-
dle adjustment.
ACKNOWLEDGEMENTS
The author would like to thank Mr Mosalam Ebrahimi
for his insight discussion on implementing the SFM
system.
REFERENCES
2d3 (2000). Boujou. http://www.2d3.com.
Digi-lab (2005). The Voodoo Cam-
era Tracker. http://www.digilab.uni-
hannover.de/docs/manual.html.
Hartley, R. and Zisserman, A. (2004). Multiple view geom-
etry in computer vision. Cambridge University Press,
2 edition.
Lourakis, M. and Argyros, A. (2009). Sba: A software
package for generic sparse bundle adjustment. 36(2).
Lowe, D. (2004). Distinctive image features from scale-
invariant keypoints. 60(2):91–110.
Mahamud, S., Hebert, M., Omori, Y., and Ponce, J. (2001).
Provably-convergent iterative methods for projective
structure from motion. In Proceedings of the IEEE In-
ternational Conference on Computer Vision and Pat-
tern Recognition 2001, pages 1018–1025.
Mouragnon, E., Lhuillier, M., Dhome, M., Dekeyser, F., and
Sayd, P. (2009). Generic and real-time structure from
motion using local bundle adjustment. 27(8):1178–
1193.
Shi, J. and Tomasi, C. (1994). Good features to track. In
Proceedings of the IEEE Conference on Computer Vi-
sion and Pattern Recognition 1994, pages 593–600.
Shum, H., Ke, Q., and Zhang, Z. (1999). Efficient bundle
adjustment with virtual key frames: a hierarchicalap-
proach to multi-frame structure from motion. In Pro-
ceedings of the IEEE Conference on Computer Vision
and Pattern Recognition 1999, volume 2, pages 538–
543.
Steedly, D. and Essa, I. (2001). Propagation of inno-
vative information in non-linear least-squares struc-
ture from motion. In Proceedings of the IEEE Inter-
national Conference on Computer Vision 2001, vol-
ume 2, pages 223–229.
Triggs, B., McLauchlan, P., Hartley, R., and Fitzgibbon, A.
(1999). Bundle adjustment: A modern synthesis. In
Proceedings of the International Workshop on Vision
Algorithms: Theory and Practice, pages 298–372.
Zhang, G., Qin, X., Hua, W., Wong, T.-T., Heng, P.-A., and
Bao, H. (2007). Robust metric reconstruction from
challenging video sequences. In Proceedings of IEEE
Conference on Computer Vision and Pattern Recogni-
tion 2007, pages 1–8.
Zhang, Z. and Shan, Y. (2003). Incremental motion esti-
mation through modified bundle adjustment. In Pro-
ceedings of IEEE International Conference on Image
Processing 2003, volume 2, pages 343–346.
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
366
