
ROBUST KEY FRAME EXTRACTION FOR 3D RECONSTRUCTION
FROM VIDEO STREAMS
Mirza Tahir Ahmed, Matthew N. Dailey
School of Engineering and Technology, Asian Institute of Technology, Pathumthani, Thailand
Jose Luis Landabaso, Nicolas Herrero
Telefonica Research, Barcelona, Spain
Keywords:
3D reconstruction, Key frame extraction, 3D video player, Geometrical robust information criterion (GRIC),
3D reconstruction degeneracy.
Abstract:
Automatic reconstruction of 3D models from video sequences requires selection of appropriate video frames
for performing the reconstruction. We introduce a complete method for key frame selection that automatically
avoids degeneracies and is robust to inaccurate correspondences caused by motion blur. Our method combines
selection criteria based on the number of frame-to-frame point correspondences, Torr’s geometrical robust
information criterion (GRIC) scores for the frame-to-frame homography and fundamental matrix, and the
point-to-epipolar line cost for the frame-to-frame point correspondence set. In a series of experiments with
real and synthetic data sets, we show that our method achieves robust 3D reconstruction in the presence of
noise and degenerate motion.
1 INTRODUCTION
Reconstructing a 3D scene from video requires choos-
ing a number of representative (key) frames from
the video stream. Automatic 3D reconstruction from
snapshots and manually extracted video frames has
been a focus of the structure-from-motion research
community for a long time, but only a few researchers
have carefully considered automatic selection of key
frames prior from a video prior to the reconstruction
process.
Estimation of 3D camera poses and recovery of
3D scene geometry are two very expensive processes
in 3D reconstruction if performed with all frames in
a video sequence. If the frames are decimated then
these processes become less expensive. Additionally,
consecutive frames may have baselines that are too
short for accurate triangulation. Another important
factor is that while the fundamental matrix provides
extremely useful information about the relationship
between two images of a general 3D structure related
by general camera motion, in degenerate cases, when
these generality assumptions for do not hold, funda-
mental matrix estimation fails.
We introduce a method for automatic key frame
selection that takes all of these factors into account. It
is based on the number of frame-to-frame point corre-
spondences obtained, Torr’s geometrical robust infor-
mation criterion (GRIC, Torr, 1998), and the point-to-
epipolar line cost for the frame-to-frame correspon-
dence set to identify key frames. In a series of exper-
iments with real and synthetic data sets, we show that
our method achieves robust 3D reconstruction in the
presence of noise and degenerate motion.
2 REQUIREMENTS
There three main reasons for extracting key frames
from video sequences: computational performance,
triangulation accuracy, and avoidance of degeneracy.
2.1 Computational Performance
The same level of 3D reconstruction can be achieved
from a few frames instead of processing all the frames
in a video sequence. This will not only improve the
performance but also the estimation of the 3D cam-
era pose and recovery of 3D scene geometry will be
computed more efficiently.
231
Tahir Ahmed M., N. Dailey M., Luis Landabaso J. and Herrero N. (2010).
ROBUST KEY FRAME EXTRACTION FOR 3D RECONSTRUCTION FROM VIDEO STREAMS.
In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 231-236
DOI: 10.5220/0002836902310236
Copyright
c
SciTePress

2.2 Triangulation Accuracy
The baseline is the line between two camera centers.
The baseline length is typically very small in consec-
utive frames. Long baselines are required for accu-
rate triangulation. The size of a 3D point’s region
of uncertainty increases as the distance between two
frames decreases. Therefore, the frame selection pro-
cess should seek to maximize the baseline between
the camera positions for key frames, subject to the
constraint that a sufficient number of correspondences
are retained.
2.3 Degeneracy Avoidance
There are two conditions for non-general camera mo-
tion and non-general position of structure known as
degenerate cases when the epipolar geometry is not
defined and methods based on estimation of the fun-
damental matrix will fail (although note that the frame
pair may still be useful for resectioning, in which we
estimate only the camera position from known 3D-2D
correspondences):
Motion Degeneracy: If the camera rotates about its
center with no translation, the epipolar geometry
is not defined.
Structure Degeneracy: When all of the 3D points in
view are coplanar, the fundamental matrix cannot
be uniquely determined from image correspon-
dences alone.
3 PREVIOUS WORK
Here we provide an overview of the most relevant re-
cent work in key frame selection. We mention the
most relevant. Seo et al. (2003) consider three fac-
tors: (a) the ratio of the number of point correspon-
dences found to the total number of point features
found, (b) the homography error, and (c) the spatial
distribution of corresponding points over the frames.
Hartley and Zisserman (2004) state that the homogra-
phy error is small when there is little camera motion
between frames. Homography error is a good proxy
for the baseline distance between two views. Seo et
al. also encourage the use of evenly distributed corre-
spondences over the entire image to obtain the funda-
mental matrix. They derive a score function from the
above mentioned factors which is used to select key
frames. The pair with the lowest score is selected as
a key frame. The authors do not discuss any measure
for degenerate cases.
Pollefeys and van Gool (2002) select key frames
for structure and motion recovery based on a motion
model selection mechanism (Torr et al., 1998) to se-
lect next key frame only once the epipolar geometry
model explains the relationship between the pair of
images better than the simpler homography model.
The distinction between the homography and the fun-
damental is based on the geometric robust informa-
tion criterion (GRIC, Torr, 1998). They discard all
frames based on degenerate cases.
Seo et al. (2008) use the the ratio of the number
of correspondences to the total number of features
found. If the ratio is close to one this means the im-
ages overlap too much and the baseline length will be
small. Under these assumptions, a frame should not
be selected as a key frame. The second measure is
the reprojection error. The pair of frames with mini-
mum reprojection error are categorized as key frames.
But as in their earlier work, no measures are taken for
degenerate cases.
4 METHOD
We treat key frame selection as constrained optimiza-
tion. Given the first frame of a video sequence, we
seek to find the successor frame that 1) has a suffi-
ciently long baseline (via a correspondence ratio con-
straint), 2) does not lead to degenerate motion or
structure, and 3) has the best estimated epipolar ge-
ometry. We introduce our methods to achieve these
criteria in this section.
4.1 Correspondence Ratio Constraint
We use Seo et al.’s (2008) correspondence ratio R
c
as
a proxy for baseline length:
R
c
=
T
c
T
f
, (1)
where T
c
is the number of frame-to-frame point fea-
tures in correspondence for the frame pair under con-
sideration, and and T
f
is the total number of point fea-
tures considered for correspondence. R
c
is inversely
correlated with camera motion: as the camera moves,
features in view tend to leave the scene, and the ap-
pearance of objects in view tends to change with per-
spective distortion, occlusion, and so on.
Although a long baseline is desirable for triangu-
lation accuracy, if the number of corresponding fea-
tures is too low, camera pose estimation accuracy will
suffer. We therefore constrain candidate key frames to
those having a correspondence ratio R
c
between up-
per and lower thresholds T
1
and T
2
. Currently, we set
these thresholds through experimentation.
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
232

4.2 Degeneracy Constraint
The relationship between a pair of images with gen-
eral camera motion and general structure is appropri-
ately defined by a fundamental matrix, whereas de-
generate camera motion is more fittingly defined by
a homography. We can thus use the relative quality
of fit to distinguish general motion from degenerate
motion. To assess the relative quality of fit, we use
Torr’s geometric robust information criterion (GRIC,
Torr, 1998). GRIC is based not only on goodness of
fit but also on the relative parsimony of the two types
of models. The score, summed over the point corre-
spondences, is
GRIC =
∑
i
ρ(e
2
i
)
i
+ λ
1
dn + λ
2
k, (2)
where ρ(e
2
i
) is a robust function
ρ(e
2
i
) = min(
e
2
i
σ
2
, λ
3
(r − d))
of the residual e
i
, d is the number of dimensions mod-
eled (d = 3 for a fundamental matrix or 2 for a ho-
mography), n is the total number of features matched
across the two frames, k is the number of degrees of
freedom in the model (k = 7 for a fundamental matrix
or 8 for a homography), r is the dimension of the data
(r = 4 for 2D correspondences between two frames),
σ
2
is the assumed variance of the error, λ
1
= log(r),
λ
2
= log(rn), and λ
3
limits the residual error.
Given a candidate key frame, we calculate the
GRIC score for the homography and the fundamental
matrix models. If the GRIC score for the homography
model is lower than the GRIC score for the fundamen-
tal matrix, we eliminate the frame as a candidate key
frame.
4.3 Key Frame Selection Criteria
We assume that the ith key frame has already been
identified as the frame with index k
i
(k
0
is just the first
frame of the video sequence). Here we describe our
method to select the next key frame k
i+1
. Let φ(k
i
)
be the set of frame indices succeeding k
i
for which
the upper and lower bounds on the correspondence
ratio R
c
are satisfied and for which the GRIC score
for the fundamental matrix model is better than the
GRIC score for the homography model. We let
k
i+1
= argmax
j∈φ(k
i
)
( f (k
i
, j)) (3)
where f (i, j) is an objective function expressing one
or more key frame goodness criteria for current key
frame i and candidate next key frame j. We con-
sider two criteria, GRIC difference and the point-to-
epipolar line cost (PELC).
4.3.1 GRIC Difference Criterion
If the GRIC score of the fundamental matrix model is
much better than that of the homography model, the
relationship between the frames is much better repre-
sented by the fundamental matrix model, indicating
a good candidate key frame. We use the normalized
GRIC difference as one possible criterion for select-
ing the next key frame:
f
G
(i, j) =
GRIC
H
(i, j) − GRIC
F
(i, j)
GRIC
H
(i, j)
, (4)
where GRIC
H
(i, j) is the GRIC score from Equation
(2) for the homography between frames i and j, and
GRIC
F
(i, j) is the GRIC score for the fundamental
matrix for frames i and j. As we shall see, this mea-
sure is good for selecting key frames because it pro-
vides very low variation in reprojection error as com-
pared to uniformly sampled frames.
4.3.2 PELC Criterion
The GRIC difference method tends to stabilize varia-
tion in reprojection error, but as we shall see in the ex-
perimental results, it has little effect on the mean error
compared to uniformly sampled frames. We analyzed
the GRIC difference scores and the point-to-epipolar
line cost over many frames in real image sequences
and observed some frames in which the variation in
the GRIC difference was very small but the variation
in the point-to-epipolar line cost (PELC) was very
high, as shown for example in Figure 1. We found
that high PELC values tended to occur due to inaccu-
rate correspondences with blurry images in our video
sequences.
We thus consider PELC as an additional criterion
for key frame selection. As we shall see in the exper-
imental results, including both the GRIC difference
and the PELC in the key frame selection criteria helps
us find key frames that are both well explained by
the epipolar geometry and have highly accurate cor-
respondences. We therefore propose the alternative
key frame score
f
GP
(i, j) = w
G
f
G
(i, j) + w
P
(σ −PELC(i, j)), (5)
where σ is the assumed standard deviation of the er-
ror and PELC is the standard geometric reconstruc-
tion error measure for the fundamental matrix (Hart-
ley and Zisserman, 2003). The weights w
G
and w
P
could be set automatically, but we currently set them
experimentally.
4.4 Algorithm Summary
The complete method for key frame selection is sum-
marized in Algorithm 1.
ROBUST KEY FRAME EXTRACTION FOR 3D RECONSTRUCTION FROM VIDEO STREAMS
233

Frames
5 10 15 20
0.25
0.2
0.15
0.1
0.05
0
0.66
0.6
0.55
0.5
0.45
0.4
0.35
0.4
0.36
0.3
0.25
0.2
GRIC
PELC
GRIC+PELC
Figure 1: Variation of GRIC difference and PELC. Frame
0 is an assumed previous key frame. The GRIC difference
is maximal for frame 13, but PELC has a local minimum
at frame 14. Since there is only a small change in GRIC
difference between frame 13 and 14 but a much improved
PELC, the GRIC+PELC method (Equation 5) selects frame
14 as the next key frame.
Algorithm 1: KEYFRAMEEXTRACTION.
1: Input: A video stream with n frames.
2: Output: Key frame index sequence k
0
, k
1
, . . .
3: i ← 0; j
∗
← 0
4: while j
∗
6= ⊥ do
5: k
i
← j
∗
;i ← i + 1; j
∗
← ⊥
6: for candidate frame j ∈ k
i
+ 1..n do
7: Match keypoints between frames k
i
and j
8: Compute H and F using RANSAC
9: Discard outlier matches
10: Calculate correspondence ratio R
c
11: if R
c
< T
min
or R
c
> T
max
then
12: continue
13: end if
14: if GRIC
H
(k
i
, j) ≤ GRIC
F
(k
i
, j) then
15: continue
16: end if
17: if f
GP
(k
i
, j) is best so far then
18: j
∗
← j
19: end if
20: end for
21: end while
5 EXPERIMENTS AND RESULTS
We performed experiments with both synthetic and
real data. The synthetic data is useful because we
can precisely identify degenerate motion and struc-
ture; the real data is useful for validate the method’s
robustness to real-world noise.
5.1 Video Sequences
Here we provide details about each experimental
video sequence.
Synthetic Data: Church. We created a 930-frame
synthetic sequence with ground truth data using
Blender (Blender Community, 2009) and a sam-
ple 3D model of a church (Blender Artists, 2000).
The scene is outdoors, with sky in the back-
ground. We inserted degenerate cases of both
types by rotating the camera view point about its
center or zooming in on planar surfaces. We ex-
tracted 3D points, projected 2D points, camera
projection matrices, and the ground truth depth for
every 2D point.
Indoor Data. These sequences were captured in-
doors at Telefonica Research, Barcelona, with a
Sony HDR camera. We performed manual cali-
bration of the camera intrinsic parameters using a
chessboard pattern.
Library. A 1500-frame sequence in the Telefon-
ica library.
Lunch Room. A 1500-frame sequence in the
Telefonica lunch room.
Imagenio. A 1500-frame sequence in the Image-
nio room at Telefonica.
Nico. A 1000-frame sequence of a person sitting
still in a chair.
Photocopy Machine. A 1200-frame sequence of
a photocopy machine.
5.2 Experiment 1: Degeneracy
In Experiment 1, we tested degenerate case identifi-
cation in the Church sequence. We processed every
10th frame as a candidate key frame. We manually
identified 26 frames consisting of degenerate motion
or structure.
Figure 2 shows the GRIC
H
(i, i + 10) and
GRIC
F
(i, i + 10) scores for each frame i consid-
ered. Frames 201–271 and 441–571 consist of pure
camera rotations, and frames 761–881 only contain
coplanar points.
Table 1 shows the detection rate and error rate
for the degenerate cases in the data set. The method
is able to identify the actual degenerate cases per-
fectly, with only 3 false positives among the 93 frames
tested.
Table 1: Detections and errors for degenerate motion and
structure detection in Experiment 1. FPs = false positives;
FNs = false negatives.
Sequence Positives FPs FNs
Church 26 3 0
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
234
Frames
0 100 200 300 400 500 600 700 800 900
4000
3500
3000
2500
2000
1500
1000
500
Automatic detection of Homography using GRIC Score
GRIC Homography
GRIC Fundamental
Cyan show 26 Degenerate Cases
Light Red show 3 False Positive
Figure 2: GRIC scores for the synthetic Church sequence.
The red dash-dot line shows GRIC
H
(i, i + 10); the green
dash-dot line shows GRIC
F
(i, i + 10). The cyan areas show
when the when the homography model is preferred. The
light red areas indicate false positives.
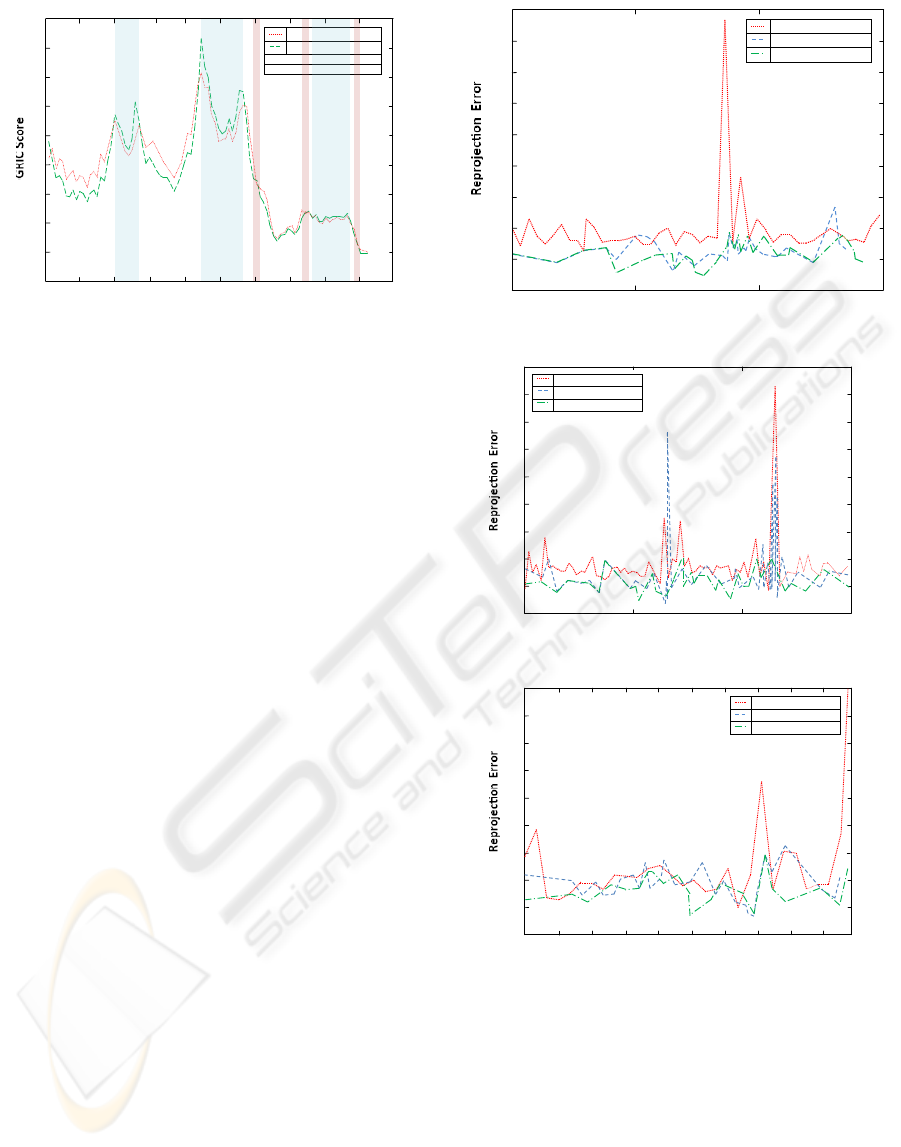
5.3 Experiment 2: 3D Reconstruction
In Experiment 2, we compared uniformly sampled
key frames, key frames selected based on the GRIC
difference score, and key frames selected using PELC
as well as the GRIC difference score. For each
sequence, we performed key frame selection then
applied Telefonica’s structure from motion pipeline
(metric reconstruction from the essential matrix for
the first pair followed by resectioning and bundle ad-
justment for subsequent key frames) to obtain a 3D
point cloud from the key frames. We computed the
root mean reprojection error for each frame then com-
puted the min, max, mean, and standard deviation
statistics over the entire sequence. A numerical com-
parison of the three methods is shown in Table 2, and
the per-frame reprojection errors are shown for three
sequences in Figure 3.
The GRIC difference score method yields much
lower reprojection error lower variance than uniform
sampling in almost every case, but the mean repro-
jection error is not much better than that for uniform
sampling, due to a few outlier frames. A manual
inspection revealed that the outlier frames tended to
be those with significant blur, leading to inaccurate
correspondences, even for the inlier correspondences.
Including PELC in the objective function eliminates
these outlier frames and leads to lower mean repro-
jection error and lower variance for all of the real se-
quences. PELC does not help much on the noise-free
synthetic sequence, however.
500 1000 1500
1.8
1.6
1.4
1.2
1
0.8
0.6
0.4
0.2
Uniformly Sampled Frames
GRIC
GRIC+PELC
Frames
Library Sequence
1.8
1.6
1.4
1.2
1
0.8
0.6
0.4
0.2
500 1000 1500
Uniformly Sampled Frames
GRIC
GRIC+PELC
Frames
Imagenio Sequence
Frames
100 200 300 400 500 600 700 800 900 1000
1.1
1.0
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
Uniformly Sampled Frames
GRIC
GRIC+PELC
Nico Sequence
Figure 3: Reprojection error comparison. Red dotted lines:
Uniform sampling. Blue dash lines: GRIC. Green dot-dash
lines: GRIC+PELC.
6 DISCUSSION AND
CONCLUSIONS
We have demonstrated the feasibility of automatic key
frame selection using a combination of constraints
based on the correspondence ratio and the GRIC
ROBUST KEY FRAME EXTRACTION FOR 3D RECONSTRUCTION FROM VIDEO STREAMS
235

Table 2: Results of Experiment 2. The GRIC+PELC method obtains the lowest mean reprojection error and lowest error
variance on all real video sequences.
Sequence Method Key frames Reprojection Error
Min Max Mean σ
Church (synthetic)
Uniform 30 0.2929 0.9608 0.4451 0.0221
GRIC 37 0.2627 0.5498 0.3878 0.0029
GRIC+PELC 29 0.2752 0.5164 0.3748 0.0026
Library
Fixed 43 0.4681 1.9595 0.6108 0.1434
GRIC 34 0.3362 0.7222 0.4738 0.0046
GRIC+PELC 37 0.2519 0.4852 0.3971 0.0022
Imagenio
Uniform 84 0.2016 1.8660 0.5415 0.0294
GRIC 79 0.2786 1.5150 0.4772 0.0363
GRIC+PELC 65 0.2493 0.6042 0.4275 0.0049
Nico
Uniform 30 0.3052 1.2125 0.4668 0.0290
GRIC 29 0.2760 0.5533 0.4032 0.0043
GRIC+PELC 29 0.2760 0.5155 0.3780 0.0031
Photocopy machine
Uniform 51 0.3210 1.7264 0.4649 0.0368
GRIC 51 0.3210 0.7955 0.4707 0.0116
GRIC+PELC 58 0.3274 0.5682 0.4324 0.0036
score for the homography and fundamental matrix,
followed by optimization of a criterion including the
GRIC difference and the point-to-epipolar line cost.
We find that the relative quality of the fundamental
matrix and homography models, represented by the
GRIC difference, is more important than the point to
epipolar line cost, but both are useful in key frame
selection when some frames are corrupted by blur.
One possible limitation of our method is the need
to specify the thresholds and weights. We currently
set these free parameters experimentally. However,
since all of the parameters are relative to the number
of correspondences obtained or the overall residual er-
ror, in principle, it should be possible to find values
that work well for most sequences and allow the user
to adjust them when necessary.
By limiting further 3D reconstruction processing
to the most informative frames, our method helps to
minimize the overall compute time of the video pro-
cessing pipeline. Telefonica is deploying the method
in an upcoming product for video surfing, which is in
the last phase of development.
Future work will focus on enhancing the system
for robustness with arbitrary videos. The key frame
selection method may have to interact with other pro-
cesses such as moving object segmentation and auto-
calibration to achieve this goal.
ACKNOWLEDGEMENTS
MTA was supported by a graduate fellowship from
the Higher Education Commission of Pakistan. We
thank Telefonica Research, Barcelona for provid-
ing the environment for this research and we thank
Guillermo Gallego and Jose Carlos for valuable sug-
gestions.
REFERENCES
Blender Artists (2000). 3D church model. Available at
http://blenderartists.org/cms/.
Blender Community (2009). Blender [open source soft-
ware]. Available at http://www.blender.org/.
Hartley, R. and Zisserman, A. (2003). Multiple View Geom-
etry in Computer Vision. Cambridge University Press,
New York, NY, USA.
Pollefeys, M. and Van Gool, L. (2002). Visual modeling
with a hand held camera. Journal of Visualization and
Computer Animation (JVCA), 13:199–209.
Seo, Kim, Doo, and Choi (2008). Optimal keyframe se-
lection algorithm for three-dimensional reconstruction
in uncalibrated multiple images. Society of Photo-
Optical Instrumentation Engineers (SPOIE), Vol. 47.
Seo, Kim, Jho, and Hong (2003). 3D estimation and
keyframe selection for match move. International
Technical Conference on Circuits/Systems, Computers
and Communications (ITC-CSCC).
Torr, P., Fitzgibbon, A., and Zisserman, A. (1998). Main-
taining multiple motion model hypotheses over many
views to recover matching and structure. pages 485–
491.
Torr, P. H. S. (1998). Geometric motion segmentation and
model selection. Phil. Trans. Royal Society of London
A, 356:1321–1340.
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
236
