RELIEF MAPPING ON CUBIC CELL COMPLEXES
Karl Apaza and Carlos Andujar
MOVING Group, Universitat Politecnica de Catalunya, Barcelona, Spain
Keywords:
Displacement mapping, Relief mapping, GPU raycasting, Quadrilateral parameterization.
Abstract:
In this paper we present an algorithm for parameterizing arbitrary surfaces onto a quadrilateral domain defined
by a collection of cubic cells. The parameterization inside each cell is implicit and thus requires storing no
texture coordinates. Based upon this parameterization, we propose a unified representation of geometric and
appearance information of complex models. The representation consists of a set of cubic cells (providing a
coarse representation of the object) together with a collection of distance maps (encoding fine geometric detail
inside each cell). Our new representation has similar uses than geometry images, but it requires storing a single
distance value per texel instead of full vertex coordinates. When combined with color and normal maps, our
representation can be used to render an approximation of the model through an output-sensitive relief mapping
algorithm, thus being specially amenable for GPU raytracing.
1 INTRODUCTION
During the last few decades much research effort
has been devoted to build parameterizations between
polygonal meshes and a variety of domains, includ-
ing planar regions, triangular or quadrilateral meshes,
polycubes and spheres. The parameterization liter-
ature has focused mainly on minimizing distortion,
guaranteeing global bijectivity, and producing seam-
less parameterizations for complex surfaces. With
very few exceptions, parameterization methods for
computer graphics compute piecewise linear map-
pings that must be encoded explicitly, typically by as-
sociating a pair of texture coordinates (u, v) to each
vertex. The explicit nature of these parameterizations
makes them non-reversible, i.e. computing the point
in the mesh represented by a point (u, v) in parame-
ter space is a costly operation, unless additional data
structures are used (García and Patow, 2008). One no-
table exception are Geometry Images (Gu et al., 2002;
Losasso et al., 2003), which allow representing geo-
metric and appearance details such as color/normal
data as separate 2D arrays, all of them sharing the
same implicit surface parametrization and thus requir-
ing no texture coordinates.
In this paper we present a method to define
projection-based parameterizations of arbitrary sur-
face meshes onto a quadrilateral domain formed by a
subset of the faces of the cubic cells intersected by the
mesh (Figure 1). The resulting parameterizations are
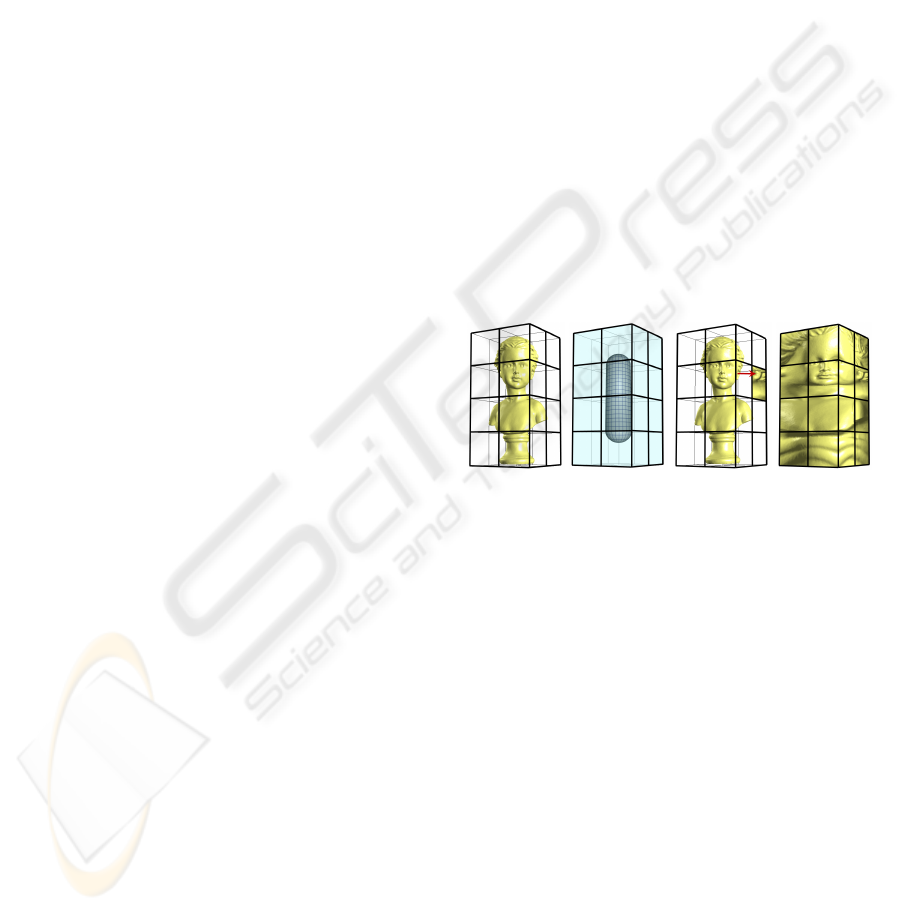
(a) (b) (c) (d)
Figure 1: Overview of our approach: (a) set of cells inter-
sected by the surface mesh; (b) the direction of projection is
defined by the normals of the shown surface; (c) each point
inside the cells is mapped onto a point on the external faces;
(d) mesh projected onto the external faces.
implicit and allow representing geometric and appear-
ance details using a collection of 2D arrays. Unlike
geometry images though, points (u, v) on our quadri-
lateral domain have associated a point P
0
= (x
0
,y
0
,z
0
)
in 3D space (on the face of a cubic cell). This fact,
along with a projection-based parameterization, al-
lows (a) encoding the coordinates of surface points
P = (x, y, z) with a single distance value ||P − P
0
|| in-
stead of storing global (x,y, z) coordinates in the 2D
array, and (b) computing quickly the intersection of
arbitrary rays with the mesh implicitly encoded by the
above distance maps.
Since we target GPU-based construction and ren-
dering algorithms, we restrict ourselves to easily in-
vertible, implicit projections. Given a point (u,v) on
the domain, we can easily compute the direction to-
wards the mesh point mapped to (u,v).
181
Apaza K. and Andujar C. (2010).
RELIEF MAPPING ON CUBIC CELL COMPLEXES.
In Proceedings of the International Conference on Computer Graphics Theory and Applications, pages 181-189
DOI: 10.5220/0002837001810189
Copyright
c
SciTePress

We use four different projection types (parallel,
perspective, axial and planar) which are chosen on
a cell-basis, according to the local neighborhood of
the cell. These projections map any point (x, y,z) in-
side the cubic cell onto a point (x
0
,y
0
,z
0
) on one of its
faces, which in turn can be expressed in local coordi-
nates (u,v) inside the face, see Figure 1(c).
Given an arbitrary surface mesh, we compute a
set of cubic cells and, using the implicit parameteri-
zation, we sample the input mesh to fill in the 2D ar-
rays with attributes such as distance, normal and color
data. Each attribute is stored as an array texture. This
provides a unified representation of the surface mesh
which allows extracting a level-of-detail approxima-
tion of the original surface. Like geometry images,
our representation can be rendered using a geometry-
based approach suitable for rasterization-based visu-
alization, which involves unprojecting each texel us-
ing the implicit projection and the stored distance
value. Moreover, a unique feature of our represen-
tation is that it is amenable for raycasting rendering,
using a GPU-based algorithm with a pattern similar to
that of relief mapping algorithms. This last rendering
approach makes our representation specially suitable
for raytracing in the GPU.
The rest of the paper is organized as follows.
Section 2 reviews previous work on implicit pa-
rameterizations and relief mapping techniques. Our
projection-based parameterization and the way we
use it to construct and render detailed meshes are dis-
cussed in Section 3. Section 4 discusses our results
on several test models. Finally, Section 5 provides
concluding remarks and future work.
2 PREVIOUS WORK
In recent years a number of methods for parameter-
izing meshes have been proposed, targeting multiple
parameter domains and focusing on different param-
eterization properties such as minimizing distortion
and guaranteeing global bijectivity. Most methods
developed so far target a planar domain and thus re-
quire cutting the mesh into disk-like charts to avoid
excessive distortions and to make the topology of the
mesh compatible to that of the domain (see (Floater
and Hormann, 2005; Sheffer et al., 2006) for a recent
survey). Parameterizations onto more complex do-
mains such as triangle or quadrilateral meshes avoid
cutting the mesh and thus provide seamless param-
eterizations. A popular base domain are simplicial
complexes obtained e.g. by just simplifying the orig-
inal triangle mesh (see e.g. (Lee et al., 1998; Guskov
et al., 2000; Praun et al., 2001; Purnomo et al., 2004)),
allowing each vertex of the original mesh to be rep-
resented with barycentric coordinates inside a ver-
tex, edge, or face of the base domain. Some re-
cent approaches target quadrilateral instead of trian-
gle meshes (Tarini et al., 2004; Dong et al., 2006).
Polycube maps (Tarini et al., 2004) use a polycube
(set of axis-aligned unit cubes attached face to face)
as parameter domain. Each vertex of the mesh is
assigned a 3D texture position (a point on the sur-
face of the polycube) from which a simple mapping
is used to look up the texture information from the
2D texture domain. Construction of the parameteri-
zation involves (a) finding a proper polycube roughly
resembling the shape of the given mesh, (b) warping
the surface of the polycube so as to roughly align it
with the surface mesh, (c) projecting each mesh ver-
tex onto the warped polycube along its normal direc-
tion, (d) applying the inverse warp function to the pro-
jected vertices, and (e) optimizing the texture posi-
tions by an iterative process. Unfortunately, no auto-
matic procedure is given for steps (a) and (b), which
are done manually. Our approach also targets a do-
main formed by axis-aligned quadrilateral faces, but
differs from polycube maps in two key points: our
parameterization is implicit and thus does not require
storing texture coordinates, and it is easily invertible
and thus it is amenable to raycasting rendering. Gu et
al. (2002) propose to remesh an arbitrary surface onto
a completely regular structure called Geometry Im-
age which captures geometry as a simple 2D array of
quantized point coordinates. Other surface attributes
like normals and colors can be stored in similar 2D ar-
rays using the same implicit surface parametrization.
Geometry images are built cutting the mesh and pa-
rameterizing the resulting single chart onto a square.
Geometry images have been shown to have numerous
applications including remeshing, level-of-detail ren-
dering and compression. Our representation has simi-
lar uses than geometry images, although construction
is much simpler and requires encoding only distance
values instead of full vertex coordinates. Solid tex-
tures (Perlin, 1985; Peachey, 1985) avoid the param-
eterization problem by defining the texture inside a
volume enclosing the object and using directly the 3D
position of surface points as texture coordinates. Oc-
tree textures (Benson and Davis, 2002) strive to re-
duce space overhead through an adaptive subdivision
of the volume enclosing the object. Although octree
textures are amenable for GPU decoding (Lefebvre
et al., 2005), a subdivision up to texel level (each
octree leaf representing a single RGB value) causes
many unused entries in its nodes, thus limiting the
maximum achievable resolution.
Space overhead grows even further when using N
3
-
GRAPP 2010 - International Conference on Computer Graphics Theory and Applications
182

trees or page tables to reduce the number of texture in-
directions (Lefebvre et al., 2005; Lefohn et al., 2006).
TileTrees (Lefebvre and Dachsbacher, 2007) also rely
on an octree enclosing the surface to be textured, but
instead of storing a single color value at the leaves,
square texture tiles are mapped onto leaf faces. Re-
sulting tiles are compactly stored into a regular 2D
texture. During rendering, each surface point is pro-
jected onto one of the six leaf faces, depending on sur-
face orientation. The resulting texture has little distor-
tion and is seamlessly interpolated over smooth sur-
faces. We also use projection onto cell faces, but our
work differs from TileTrees in two key aspects. On
the one hand, we do not restrict ourselves to parallel
projection; we also use perspective and axial projec-
tions whenever appropriate. On the other hand, our
approach is suitable for encoding geometry as dis-
placement maps. Note that this does not apply to Tile-
Trees because determining the face a surface point P
inside a cell must be projected onto requires knowl-
edge about both the P coordinates and its normal vec-
tor.
Relief mapping (Policarpo et al., 2005) has been
shown to be extremely useful as a compact represen-
tation of highly detailed 3D models. All the neces-
sary information for adding surface details to polyg-
onal surfaces is stored in RGBA textures, with the
alpha channel storing quantized depth values. The
technique uses an inverse formulation based on a ray-
heightfield intersection algorithm implemented on the
GPU. For each ray, the intersection is found by a lin-
ear search followed by a binary search along the ray.
This algorithm has been extended in (Policarpo and
Oliveira, 2006) to render non-height-field surface de-
tails in real time. This new technique stores multi-
ple depth and normal values per texel and generalizes
their previous proposal for rendering height-field sur-
faces. Baboud and Décoret (Baboud and Décoret,
2006) obtain more accurate intersections than the lin-
ear search of (Policarpo et al., 2005) by precom-
puting a safety radius per-texel, this way larger steps
can be made. Moreover, the height fields are built
using inverse perspective frusta, which help improve
the sampling on certain regions. Omni-directional re-
lief impostors (Andujar et al., 2007) represent surface
meshes by pre-computing a number of relief mapped
polygons distributed around the object. In runtime,
the current view direction is used to select a small sub-
set of the pre-computed maps which are then rendered
using relief mapping techniques.
The relationship of our approach with displace-
ment and relief maps is twofold. On the one hand,
displacement mapping also relies on a simple projec-
tion (parallel projection) plus depth values to encode
fine geometric details. On the other hand, all accel-
eration techniques for computing the intersection of
a ray with the surface implicitly encoded by the dis-
tance map can be adopted to render our representa-
tion, by just projecting each sample along the ray onto
the texture domain. These acceleration methods in-
clude, among others, linear search plus binary search
refinement (Policarpo et al., 2005), varying sampling
rates (Tatarchuk, 2006), and precomputed distance
maps (Baboud and Décoret, 2006; Donnelly, 2005).
3 OUR APPROACH
3.1 Notation
Let M be the input mesh, and let V be the set of cubic
cells in an N × N × N grid subdivision of the axis-
aligned bounding cube of M. Cells in V can be clas-
sified as white (W) cells (those outside M), black (B)
cells (those inside M), and grey (G) cells (those with
non-empty intersection with the boundary of M). A
face of a G cell shared with a W cell will be referred
to as external face. Otherwise it will be called internal
face. A G cell has between zero and six external faces.
G cells with at least one external face will be referred
to as border G cells (BG cells for short). Likewise,
G cells with no external faces will be referred to as
interior G cells (IG cells).
3.2 Parameterization
Our mapping is based on projecting the boundary of
M onto the external faces of BG cells and the internal
faces of IG cells. We will collectively refer to these
faces as domain faces. Each G cell is assigned a pro-
jection type which projects points inside the cell onto
the subset of domain faces of the cell. According to
the internal/external status of its six faces, a G cell
can have one out of 2
6
configurations, which can be
grouped under rotations into ten base cases (Figure 4).
We use four different projection types (Figure 2):
• Parallel projection: defined by a vector ~v estab-
lishing the direction of projection (DoP).
• Planar projection: defined by a plane Π with equa-
tion ax +by+cz+d = 0. A point P inside the cell
will be projected along the normal ~n = (a, b, c) or
the opposite normal −~n depending on the halfs-
pace where P is located, i.e. depending on the
sign of ~nP + d.
• Perspective projection: defined by a point C es-
tablishing the center of projection (CoP). A point
RELIEF MAPPING ON CUBIC CELL COMPLEXES
183

(a) (b) (c) (d)
Figure 2: The four types of projections we consider inside
each cell: (a) parallel, (b) planar, (c) perspective, (d) axial.
Figure 3: The axial parameterization maps straight line seg-
ments onto planar curves. A sample case using axial pro-
jection from the bottom back edge onto two external faces
(left); this projection maps the blue segment onto a planar
curve on the top face of the cubic cell (right).
P inside the cell will be projected along the direc-
tion CP.
• Axial projection: defined by an axis a parallel to
one of the coordinate axes. For example, points
on an axis parallel to the X axis has points with
the form (λ, a
y
,a
z
) for some λ ∈ R. A point P
inside the cell will be projected along the direction
(λ,P
y
− a
y
,P
z
− a
z
).
In all cases points inside the cell are projected onto
the cell’s faces. The first three types of projections de-
fine linear mappings, projecting mesh triangles inside
the cell onto triangles on the support plane of each
domain face, whereas the last projection type leads to
a non-linear mapping, projecting mesh triangles onto
triangular patches with curved edges (Figure 3). This
non-linearity property poses no problem to the ren-
dering algorithm, as discussed below.
Each parameterization is local to a cell c in the
sense that each G cell has a single projection type, and
only the geometry inside a G cell is projected onto its
domain faces. We now discuss, for each base case, the
Case 0 Case 1 Case 2a Case 2b Case 3a
Case 3b Case 4a Case 4b Case 5 Case 6
Figure 4: Configurations of a G cells can be grouped into
the ten base cases shown. For each case we show a G cell
(with colored faces) and its non-empty 6-connected cells.
type of projection we use, which constraints affect the
parameter (~v,C,Π,a) controlling the projection (so as
to guarantee that points inside the cell are projected
only onto its domain faces), and how to compute a
suitable value for that parameter (Figure 5).
Case 0. All six faces are external. We use a perspec-
tive projection with the CoP C being any point in-
side the cell. This point can be computed simply
as the cell’s center.
Case 1. All faces are external except for one internal
face F. We also use a perspective projection, this
time C being any point on F. Our current imple-
mentation computes C as the middle point of F.
Case 2a. All edges are shared by external faces, ex-
cept for one internal edge e. Again, we use per-
spective projection with C being any point on e.
Our implementation uses the middle point of e.
Case 2b. Only two internal faces F
1
,F
2
in opposite
directions. We use an axial projection, taking any
axis defined joining a point on F
1
with a point on
F
2
. Our current implementation uses the axis de-
fined by joining the middle points of F
1
and F
2
.
Case 3a. Three external faces and only two internal
edges e
1
,e
2
. We also use an axial projection, with
the axis defined by joining a point on e
1
and a
point on e
2
. Our current implementation simply
uses the midpoints of e
1
and e
2
.
Case 3b. Three internal faces meeting at a vertex v.
We use perspective projection from v.
Case 4a. This case is the complementary of case 2b,
with two parallel external faces F
1
,F
2
. We use a
planar projection with Π being a plane parallel to
F
1
and F
2
. Our current implementation uses the
plane going through the cell’s center.
Case 4b. This case is the complementary of case 2a,
with a single external edge e
1
. For this case we
use the axial projection provided by the opposite
edge in the cell.
Case 5. This case is the complementary of case 1,
with a single external face F. We use a parallel
projection with ~v being the normal of F.
Case 6. This case, which is the complementary of
case 0, is handled using the same perspective pro-
jection.
3.3 Construction
We first assume that a given grid resolution N has
been fixed and discuss how to compute the G cells
of the resulting N × N × N grid (Section 3.3.1), and
how to sample properties to build the texture using the
GRAPP 2010 - International Conference on Computer Graphics Theory and Applications
184

Case 0 Case 1 Case 2a Case 2b Case 3a
Case 3b Case 4a Case 4b Case 5 Case 6
Figure 5: Projection type for each basic G cell configura-
tion. Points inside each G cell are projected onto the col-
ored faces using projection lines perpendicular to the shown
spherical/cylindrical/planar surface.
projections described above (Section 3.3.2). Then, a
simple algorithm for choosing a proper value for N is
presented in Section 3.3.3.
3.3.1 Computing the G Cells
This step simply accounts for dividing the bound-
ing cube of the input mesh M into an N × N × N
grid, and classifying the resulting cubic cells as W,
G or B. This can be done either in the CPU, follow-
ing the discretization algorithm described in (Andujar
et al., 2002), or in the GPU, using a voxelization algo-
rithm (Eisemann and Décoret, 2008). Our current im-
plementation uses the CPU-based approach because
it also provides, for each G cell, the list of faces inter-
secting it, which greatly accelerates the sampling of
surface attributes discussed below.
3.3.2 Sampling Surface Properties
We now describe a GPU-based algorithm for sam-
pling surface properties to fill the 2D texture associ-
ated with each domain face. The algorithm traverses
all G cells {c
i
} and all the domain faces of each c
i
.
The basic idea is to render the geometry inside the
cell onto a texture, using a shader for computing the
projection.
The CPU-based part of the rendering algorithm
proceeds through the following steps:
1. Setup a frame buffer object (FBO) and a viewport
transformation matching the desired texture size.
2. Setup an orthographic camera facing the domain
face c
i
to be sampled.
3. Set the uniform variables encoding the cubic cell
and its projection type, to make this information
available to the geometry and fragment shaders.
4. Draw the mesh triangles intersecting the cell.
The vertex shader leaves the input vertices untrans-
formed, the projection being performed in a geome-
try shader. We have adopted this solution because,
due to the non-linearity of the mapping used for cases
2b, 3a and 4b, mesh triangles must be tessellated by
subdividing large mesh edges prior to projecting its
vertices. The geometry shader thus performs these
steps:
1. If the current cell uses axial projection (cases 2b,
3a, 4b), tessellate the triangle by uniformly subdi-
viding the edges longer than a user-defined thresh-
old.
2. Use the projection type to project the vertices into
the support plane of the domain face c
i
to be filled.
For mesh triangles whose projection spans multi-
ple domain faces, some projected vertices might
lie outside the domain face, but OpenGL’s clip-
ping will take care of these cases.
3. For each primitive, emit the projected vertices, en-
coding its original position as texture coordinates.
Finally, the fragment shader simply encodes in the
output color the attribute to be sampled. Dis-
tance maps simply encode the distance between mesh
points P = (x, y, z) and their projection P
0
= (x
0
,y
0
,z
0
).
Note that these distances must be computed on a per-
fragment basis, as they do not interpolate linearly
when using e.g. perspective projection (cases 0, 1,
2a, 3b, Figure 5). Since the mapping is non-bijective,
multiple surface points might project onto the same
texel. In these cases the texel must encode the dis-
tance to the closest surface point. This is accom-
plished by simply setting the fragment depth to the
computed distance, so that OpenGL’s depth test will
discard occluded samples. Other surface signals such
as color and normal data are sampled in a similar way
(Figure 6).
3.3.3 Choosing a Proper Grid Size
A fine grid provides a better approximation of the sur-
face mesh, each G cell having a simpler region inside
and thus more likely to be represented faithfully by
the distance maps. However, increasing the number
of cells also increases storage space and adds some
overhead to the rendering algorithm. Our algorithm
for choosing a proper grid resolution N strives to min-
imize the number of surface elements that map onto
the same texel. A simple estimation for this number
can be computed by running the sampling algorithm
above but using the stencil buffer to count the num-
ber of fragments projecting onto the same texel. So
we start with an 1 × 1 × 1 grid and compute the ratio
of occluded fragments. If the ratio is above a user-
RELIEF MAPPING ON CUBIC CELL COMPLEXES
185

(a) (b) (c)
Figure 6: Sampling attribute values: (a) model inside a sin-
gle cubic cell; (b) sampled distance ||P−P
0
|| represented as
color temperature; (c) sampled normals.
defined threshold, we increase (e.g. doubling) the res-
olution in each direction and repeat the above steps
until the ratio is below the threshold, or a maximum
N
max
is reached.
3.4 Representation
Our representation consists of:
• A lookup table encoding the G cells, and the pro-
jection type for each G cell.
• A collection of 2D textures (one for each domain
face) encoding the distance maps. Since all these
textures have the same size, they can be packaged
as an array texture (GL_EXT_texture_array ex-
tension). An array texture is accessed by shaders
as a single texture unit. A single layer is selected
using the r texture coordinate, and that layer is
then accessed as though it were a 2D texture us-
ing (s,t) coordinates.
• An array texture for each additional surface signal
(color, normal).
3.5 Rendering
Our representation can be rendered using both a direct
approach which reconstructs a triangle mesh approxi-
mating the object on-the-fly, or a raycasting approach
which relies on intersecting viewing rays with the dis-
tance maps.
3.5.1 Geometry-based Rendering
Our representation can be rendered by reconstructing
a triangle mesh on the fly using an algorithm similar
to that of Geometry Images (Gu et al., 2002). The
idea is to visit all texels of the distance maps and cre-
ate a pair of triangles for each 2x2 group of texels.
Each texel (u,v) of a domain face is associated with a
point P
0
= (x
0
,y
0
,z
0
) on the surface of a G cell, which
can be computed by a simple transformation from lo-
cal to global coordinates. Using the distance d stored
at texel (u, v) and the projection type of the G cell,
we can unproject point P
0
to get a point of the surface
mesh. Level-of-detail rendering is implemented by
mip-mapping the distance maps. During rendering,
the normal-map signal is rasterized over the triangles
by hardware, using bilinear filtering of each quad in
the normal map. This reconstruction type allows our
representation to have similar uses than geometry im-
ages.
3.5.2 Raycasting Rendering
A more interesting feature of our representation is the
output-sensitive rendering through raycasting. Re-
lief mapping (Policarpo et al., 2005) can be easily
generalized to compute the intersection of a ray with
the surface implicitly encoded by distance maps built
from arbitrary projections. The classic approach for
relief mapping is to compute the ray-heightfield in-
tersection by sampling points along the ray, first us-
ing linear search to find a sample inside the object,
and then refining the intersection point through bi-
nary search, Figure 7(a). For each sampled point,
the height of the sample is compared with the depth
stored in the relief map to determine whether the sam-
ple is inside or outside the heightfield. This idea
can be trivially extended from heightfields to distance
maps constructed from the projection types discussed
in Section 3.2. We also sample points P
i
along the ray,
see Figure 7(b). Each sample P
i
is projected onto the
corresponding domain face to compute the projected
point P
0
i
which is converted to local (u
i
,v
i
) coordi-
nates. The distance value d stored at (u
i
,v
i
) is dequan-
tized and then compared with the distance ||P
i
− P
0
||
to check whether the sampled point is inside or out-
side the object. The distribution of tasks between the
different processors is as follows.
The CPU-based part of the rendering algorithm
proceeds through the following steps:
1. Bind the array textures encoding dis-
tance/color/normal maps to different texture
units, and bind also the texture encoding the LUT
of cubic cells and projection types to another
texture unit.
2. Draw the frontfaces of the G cells, just to ensure
that a fragment will be generated for any viewing
ray intersecting the underlying object.
The vertex shader performs no significant computa-
tions. The most relevant part of the rendering relies
on the fragment shader, which performs these steps:
1. Compute the viewing ray.
2. Sample points on the ray using linear search to
find the first sample, if any, inside the object. For
GRAPP 2010 - International Conference on Computer Graphics Theory and Applications
186
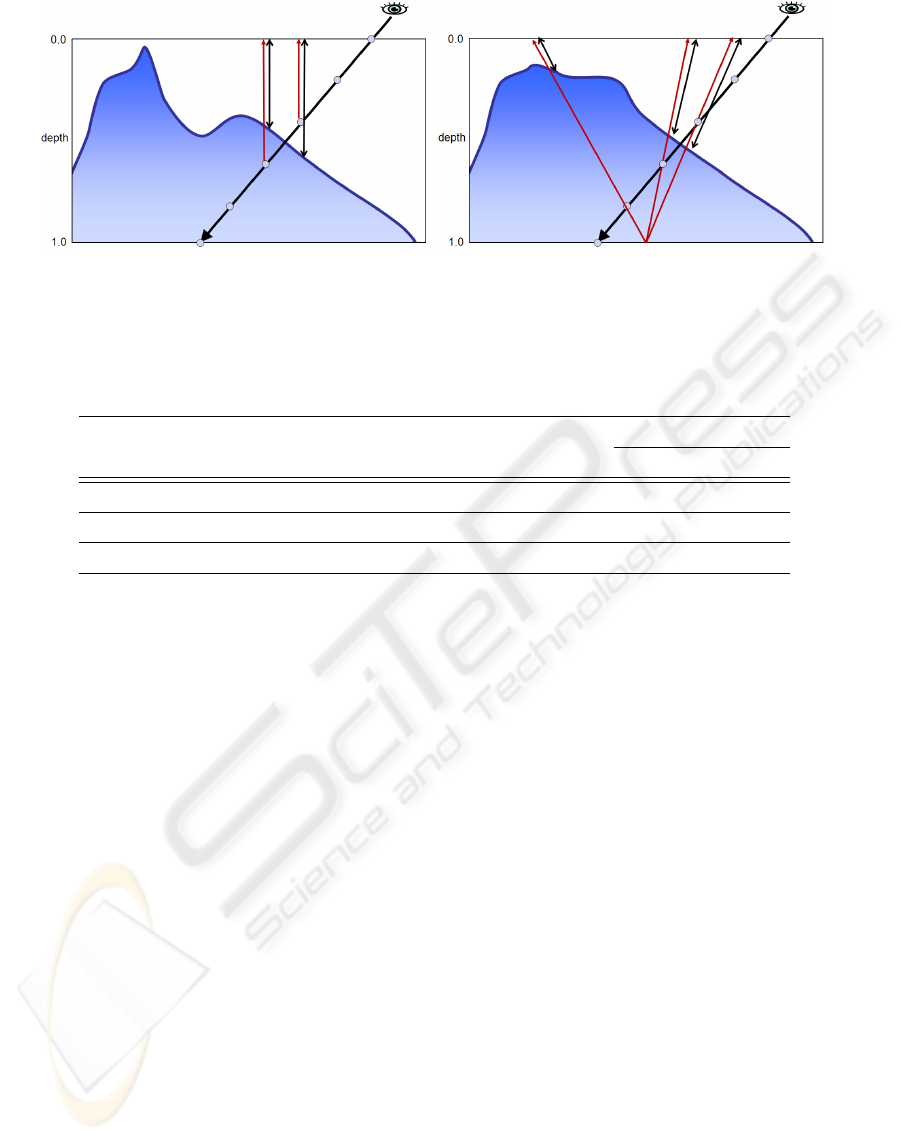
(a) (b)
Figure 7: Computing ray-surface intersections by sampling points along the ray: (a) surface encoded as a heightfield (b)
surface encoded using a perspective projection. The red arrows indicate the direction of projection; black arrows show the
distance stored in the texture, which is checked against the real distance from the sampled point on ray to the projection plane.
Table 1: Construction times for the test models.
# Faces # G cells # Domain Texture Total Construction times
faces size size G cells Sampling
Egea 16.5K 18 42 64x64 336KB < 1s < 1s
Squirrel 20K 18 42 64x64 336KB < 1s < 1s
Moai 20K 20 48 64x64 384KB < 1s < 1s
Pensatore 1M 1 6 128x128 192KB 2 s 3 s
each sample point, we identify the cell c contain-
ing the sample, retrieve the projection P associ-
ated with the cell, and apply P to project the sam-
ple onto domain face. Stop as soon as a sample
inside the object is found. Otherwise, the ray does
not intersect the surface and hence the fragment is
discarded.
3. Refine the intersection point using binary search,
as in classic relief mapping.
4. Use the texture coordinates (u, v) at the intersec-
tion point to lookup surface signals such as color
and normal data.
Most acceleration methods for relief mapping can be
also adopted to our approach. In particular, interval
mapping can be integrated into our approach with lit-
tle effort.
4 RESULTS
We have implemented a prototype version of the pro-
posed algorithms and we have tested them with de-
tailed models from the Aim@Shape repository.
Table 1 shows full construction times, including
the computation of the cells intersected by the mesh
and the sampling process required to build the dis-
tance and normal maps. Note that these times are
highly competitive and clearly outperform construc-
tion times of state-of-the-art parameterization algo-
rithms. The storage space required to store the array
textures has been computed using 2 bytes to quantize
distance values (Table 1). In all cases a low-resolution
grid was enough to obtain a parameterization with lit-
tle or no overlap between mesh triangles.
Figure 8 shows the results of our raycasting ren-
dering algorithm. Note that differences are hardly
noticeable. Rendering times measured on an Nvidia
GTX 280 are shown in Table 2. Rendering times are
clearly dominated by the number of fragments to be
processed. How these rendering times compare to
rendering the input model depends basically on the
complexity of the model and its screen projection.
Simple models with large screen projections are ren-
dered much faster using the original mesh, whereas
complex models with small screen projection render
much faster with our output-sensitive approach. Ta-
ble 2 also shows the number of ray intersections that
can be computed per second. It is worth to remark
that the ray throughput we achieve also holds for re-
flected and refracted rays. The rendering time for
drawing the model as is or its reflection on a curved
mirror is roughly proportional to the number of ray in-
tersections. This unique feature makes our approach
RELIEF MAPPING ON CUBIC CELL COMPLEXES
187

Figure 8: Results using raycasting rendering (bottom row)
compared with the original model (top row)
Table 2: Rendering times using raycasting on a 512x512
viewport, and number of ray-surface intersections.
Egea Squirrel Moai Pensatore
Frame rate 107 fps 112 fps 99 fps 111 fps
Rays/s 28M 29M 26M 29M
particularly suitable for ray-tracing in the GPU. Note
that competing representations such as relief-mapped
meshes only perform well once the fragment coordi-
nates and interpolated texture coordinates have been
computing during the rasterization stage; otherwise,
additional spatial data structures are required to com-
pute the ray-mesh intersection.
Unlike polycube maps (Tarini et al., 2004), our
representation can be computed fully automatically.
Furthermore, since the parameterization is implicit
and quickly reversible from the distance maps, the
original mesh is not required to render the surface,
and the surface can be rendered efficiently using a
raycasting approach. The simplicity of our approach
comes at a price though. Since we leave out optimiza-
tion steps performed during construction of polycube
maps and the flexibility offered by storing explicit
texture coordinates, our parameterization might suf-
fer from higher distortion.
5 CONCLUSIONS
The main contributions of the paper are (a) a
projection-based method for defining implicit param-
eterization of surface meshes onto an automatically
computed set of cubic cells, (b) a unified representa-
tion of detailed meshes based on the above param-
eterization using array textures encoding projection
distances and other surface signals such as normals
and color, (c) an efficient GPU-based algorithm for
sampling these signals, and (d) a rendering algorithm
which generalizes relief mapping to arbitrary projec-
tions. Since we target GPU-based construction and
rendering, we restrict ourselves to easily invertible,
implicit projections, at the expense of bijectivity and
distortion minimization guarantees. Our approach
is oriented towards arbitrarily-detailed models whose
main features are roughly well captured by a low res-
olution grid. Complex surfaces with many thin parts
such as bones or pipes might require a high resolution
grid to sample faithfully the surface, thus making our
approach less attractive for representing these models.
There are several directions that can be pursued
to extend the current work. The parameters defining
each projection type can be optimized by taking into
account the distribution of the geometry inside each G
cell, at the expense of higher construction times. For
instance, the CoP used by case 0 can be computed as
the centroid of the part of the mesh intersecting the
cell, instead of taking just the cell’s center. We would
like to further compare our projection with the projec-
tor operator proposed by Tarini et al. (2004). Leaving
out further optimization steps, the projector operator
is also implicitly defined as in our case. Another ob-
vious extension is to use an octree instead of equal-
sized cubic cells. The criteria for grid refinement can
be applied for each octree node with little effort. This
would result in G cells at different levels and with dif-
ferent texture sizes. Since array textures require each
2D texture layer to have the same size, multiple array
textures will be needed, one for each different texture
size.
ACKNOWLEDGEMENTS
This work has been partially funded by the Span-
ish Ministry of Science and Technology under grant
TIN2007-67982-C02. All test models were provided
by the AIM@SHAPE Shape Repository.
REFERENCES
Andujar, C., Boo, J., Brunet, P., Fairen, M., Navazo,
I., Vazquez, P., and Vinacua, A. (2007). Omni-
directional relief impostors. Computer Graphics Fo-
rum, 26(3):553–560.
Andujar, C., Brunet, P., and Ayala, D. (2002). Topology-
reducing simplification through discrete models. ACM
Transactions on Graphics, 20(6):88–105.
Baboud, L. and Décoret, X. (2006). Rendering geometry
with relief textures. In Proc. of Graphics Interface,
pages 195–201, Toronto, Canada.
GRAPP 2010 - International Conference on Computer Graphics Theory and Applications
188

Benson, D. and Davis, J. (2002). Octree textures. ACM
Transactions on Graphics (TOG), 21(3):785–790.
Dong, S., Bremer, P.-T., Garland, M., Pascucci, V., and
Hart, J. C. (2006). Spectral surface quadrangulation.
ACM Transactions on Graphics, 25(3):1057–1066.
Donnelly, W. (2005). Per-pixel displacement mapping
with distance functions. In GPU Gems 2: Program-
ming Techniques for High-Performance Graphics and
General-Purpose Computation, pages 123–136.
Eisemann, E. and Décoret, X. (2008). Single-pass gpu solid
voxelization for real-time applications. In GI ’08:
Proceedings of graphics interface 2008, pages 73–80.
Floater, M. S. and Hormann, K. (2005). Surface parameter-
ization: a tutorial and survey. In N. A. Dodgson, M.
S. F. and Sabin, M. A., editors, Advances in Multireso-
lution for Geometric Modelling, Mathematics and Vi-
sualization, pages 157–186. Springer, Berlin.
García, I. and Patow, G. (2008). Igt: inverse geometric tex-
tures. ACM Transactions on Graphics, 27(5):1–9.
Gu, X., Gortler, S. J., and Hoppe, H. (2002). Geometry
images. ACM Transactions on Graphics, 21(3):355–
361.
Guskov, I., Vidim
ˇ
ce, K., Sweldens, W., and Schröder, P.
(2000). Normal meshes. In SIGGRAPH’00, pages
95–102.
Lee, A. W. F., Sweldens, W., Schröder, P., Cowsar, L.,
and Dobkin, D. (1998). Maps: multiresolution adap-
tive parameterization of surfaces. In SIGGRAPH’98,
pages 95–104.
Lefebvre, S. and Dachsbacher, C. (2007). Tiletrees. In
Proceedings of the 2007 symposium on Interactive 3D
graphics and games, page 31. ACM.
Lefebvre, S., Hornus, S., and Neyret, F. (2005). Octree Tex-
tures on the GPU. GPU gems, 2:595–613.
Lefohn, A., Sengupta, S., Kniss, J., Strzodka, R., and
Owens, J. (2006). Glift: Generic, efficient, random-
access GPU data structures. ACM Transactions on
Graphics (TOG), 25(1):60–99.
Losasso, F., Hoppe, H., Schaefer, S., and Warren, J. (2003).
Smooth geometry images. In SGP ’03: 2003 Eu-
rographics/ACM SIGGRAPH symposium on Geome-
try processing, pages 138–145. Eurographics Associ-
ation.
Peachey, D. (1985). Solid texturing of complex surfaces.
ACM SIGGRAPH Computer Graphics, 19(3):286.
Perlin, K. (1985). An image synthesizer. ACM SIGGRAPH
Computer Graphics, 19(3):296.
Policarpo, F. and Oliveira, M. M. (2006). Relief mapping
of non-height-field surface details. In Proc. of ACM
Symp. on Interactive 3D Graphics and Games, pages
55–62.
Policarpo, F., Oliveira, M. M., and Comba, J. (2005). Real-
time relief mapping on arbitrary polygonal surfaces.
In Proc. of ACM Symposium on Interactive 3D Graph-
ics and Games, pages 155–162.
Praun, E., Sweldens, W., and Schröder, P. (2001). Con-
sistent mesh parameterizations. In SIGGRAPH ’01,
pages 179–184.
Purnomo, B., Cohen, J. D., and Kumar, S. (2004). Seam-
less texture atlases. In SGP ’04: Proceedings of the
2004 Eurographics/ACM SIGGRAPH symposium on
Geometry processing, pages 65–74.
Sheffer, A., Praun, E., and Rose, K. (2006). Mesh param-
eterization methods and their applications. Founda-
tions and Trends in Computer Graphics and Vision,
2(2):105–171.
Tarini, M., Hormann, K., Cignoni, P., and Montani, C.
(2004). Polycube-maps. In SIGGRAPH ’04 , pages
853–860.
Tatarchuk, N. (2006). Dynamic parallax occlusion mapping
with approximate soft shadows. In I3D ’06: Proceed-
ings of the 2006 symposium on Interactive 3D graph-
ics and games, pages 63–69.
RELIEF MAPPING ON CUBIC CELL COMPLEXES
189
