UNDERSTANDING PHOTOGRAPHIC COMPOSITION THROUGH

DATA-DRIVEN APPROACHES

Dansheng Mao, Ramakrishna Kakarala, Deepu Rajan

School of Computer Engineering, Nanyang Technological University, Singapore

Shannon Lee Castleman

School of Arts, Design and Media, Nanyang Technological University, Singapore

Keywords:

Computational Aesthetics, Computer vision, Machine learning, Visual perception, Saliency model.

Abstract:

Many elements contribute to a photograph’s aesthetic value, include context, emotion, color, lightness, and

composition. Of those elements, composition, which is how the arrangement of subjects, background, and

features work together, is both highly challenging, and yet amenable, for understanding with computer vision

techniques. Choosing famous monochromic photographs for which the composition is the dominant aesthetic

contributor, we have developed data-driven approaches to understand composition. We obtain two novel

results. The ﬁrst shows relationships between the composition styles of master photographers based on their

works, as obtained by analyzing extracted SIFT features. The second result, which relies on data obtained from

eye-tracking equipment on both expert photographers and novices, shows that there are signiﬁcant differences

between them in what is salient in a photograph’s composition.

1 INTRODUCTION

There are many contributors to aesthetics in photogra-

phy, including color, lightness, emotion, context, and

composition. What is interesting about composition

from a computer vision perspective is that it is highly

challenging to understand, and yet, being based on

geometrical arrangements of subjects, features, and

background, also amenable to image analysis. Com-

position has traditionally been studied by qualitative

means (Zakia, 2007). In this paper, we take a data-

driven approach, using both feature extraction with

computer vision techniques and statistical analysis of

eye-tracking data. Figure 1 shows, for illustrative pur-

poses, the two types of data that we use.

Much prior work in computational aesthetics re-

lated to our paper is devoted to studying paint-

ings, rather than photographs. Taylor et al.’s (Taylor

et al., 1999) fractal analysis of Jackson Pollock’s drip

paintings, later disputed by Jones-Smith and Mathur

(Jones-Smith and Mathur, 2006), was followed by

Rockmore et al (Lyu et al., 2004), who used multi-

resolution visual analysis of brush strokes to iden-

tify how many apprentices worked on a master paint-

ing. Bressan et al (Bressan et al., 2008) also work on

(a) Scale invariant fea-

tures.

(b) Human ﬁxation

locations.

Figure 1: Examples of the two data types used in this paper:

extracted SIFT features are shown in (a) on a photograph by

Andre Kertesz, and eye-tracking data are shown in (b) on a

photograph by Mary Ellen Mark (Please see colour images

in PDF).

paintings, and provide a multidimensional scaling ap-

proach to describing the similarities between painters

based on their works. Much work has been devoted to

measuring facial attractiveness from images, see (Ka-

gian et al., 2006) and the references therein. Aesthetic

analysis of photographs from user ratings has been

discussed by Datta et al(Datta et al., 2006). In their

approach, the aesthetic value of an image is predicted

by a classiﬁer trained on image ratings from users on

such sites as Photo.net.

While this approach is useful to predict ratings

425

Mao D., Kakarala R., Rajan D. and Lee Castleman S. (2010).

UNDERSTANDING PHOTOGRAPHIC COMPOSITION THROUGH DATA-DRIVEN APPROACHES.

In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 425-430

DOI: 10.5220/0002842104250430

 SciTePress

with a particular group of users, it does not illuminate

the role of composition. The black and white pho-

tographs of the master photographers known for their

strong composition, such as Henri Cartier-Bresson,

would not rate highly with that approach. Recent

work on photographic visual saliency by Judd et al.

(Judd et al., 2009) uses eye-tracking data, which is

fed as ground-truth data into a SVM trainer for a

saliency predictor. However, their study did not fo-

cus on photographs known for composition, nor did it

distinguish expert photographers from novices, both

of which we do in this paper.

Our work looks into the relationship of photo-

graphic composition among master photographers,

and also examines the differences in saliency between

expert photographers and novices. The relationships

in composition style of eight master photographers is

described with the aid of multi-dimensional scaling.

Speciﬁcally, the similarity between any two photogra-

phers is measured with the Fisher kernel method (Per-

ronnin and Dance, 2007), which uses features extractd

from their photographs and modelled by a Gaussian

mixture distribution. We also describe differences be-

tween what experts ﬁnd salient in a composition and

what novices do by analyzing data obtained with eye-

tracking equipment. We use receiver operating char-

acteristic (ROC) analysis to describe how consistent

novices are with each other, how consistent experts

are, and how well each group predicts the other.

2 PHOTOGRAPHER DATASET

We collected 106 monochromic photographs of 8 fa-

mous photographers, who are known for their com-

position styles, by scanning images from published

books. The images have about 1 megapixel per im-

age. We call this the Π dataset. Another dataset,

denoted Ω, has 19 photographs, each with resolu-

tion of around 3K pixels per image, was collected

from the Microsoft Bing image search engine to make

sure each selected photographer has at least 15 pho-

tographs. Figure 2 gives a sample photograph of the

each photographer used.

Since we reduce the photograph size prior to

feature-based data analysis to avoid redundant fea-

tures being extracted, the evaluation for our feature-

based approach involved both Π and Ω. For the exper-

iment with eye-tracking equipment describe in Sec-

tion 4, the photographs shown to the user for appre-

ciation on a 1024 × 768 monitor were from Π, and

were scaled equally in each dimension in order to ﬁt

the full screen.

(a) W. Eugene Smith. (b) August

Sander.

Doiseneau.

(e) Bruce Davidson. (f) Mary Ellen

Mark.

(g) Henri Cartier Bresson. (h) Andre Kertesz.

Figure 2: Sample photographs from the dataset. Though

the resolutions varies with different photographs, they have

been resized with aspect ratios preserved for viewing here.

(a) “Dancer” by An-

dre Kertesz.

(b) “Farmer” by

August Sander.

Figure 3: The most dissimilar pair of photographs in com-

position style from the 8 different photographers in our

dataset. Note that the ”Dancer” photograph is primarily hor-

izontal, while the ”Farmer” is vertical.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

426

3 UNDERSTANDING WITH

FEATURE-BASED DATA

Photographic composition relies on arrangements of

attributes (colors, texture) and features (lines, curves,

faces) that are identiﬁable by computer vision tech-

niques. In computer vision, the bag of words (BoW)

model with the attributes and features is a popular rep-

resentation for image categorization. The main idea is

to characterize an image with the histogram of the vi-

sual words, and the histogram vector could be used

with any discriminative classiﬁer or categorizer. A

drawback of the BoW method is that the computa-

tional complexity is often high, since it relies on local

features extracted from the image.

3.1 Fisher Kernel based Image

Representation

Within the ﬁeld of pattern classiﬁcation, the Fisher

kernel is a powerful framework which combines as-

pects of generative and discriminative approaches

(Jaakkola and Haussler, 1998). Let p be a pdf which

models the distribution of the low level features in any

image, and let λ denote the parameters that the model

relies on. Let X = {x

, t ∈ [1, T]} denote a set of low-

level features extracted from an image. The features

are then represented as the following gradient vector:

= ∇

log p(X|λ) = ∇

t=1

log p(x

|λ). (1)

In our case, p is a Gaussian Mixture Model (GMM)

trained on the set of photographs that we chose. Intu-

itively, the gradient G

of the log-likelihood describes

the direction in which parameters should be modiﬁed

to best ﬁt the data. It transforms a variable length

sample X into a ﬁxed length vector whose size is only

dependent on the number of parameters in the pdf

model. Hence, G

can be fed into any discrimina-

tive classiﬁer. For those classiﬁers that measure the

similarity by the inner product technique, it is neces-

sary to normalize the input vector. In (Jaakkola and

Haussler, 1998), the Fisher information matrix F

(X)

is deﬁned for that purpose as follows (with

′

denoting

transpose):

(X) = E

[∇

log p(X|λ)∇

log p(X|λ)

′

]. (2)

Because of the cost associated with its composition

and inversion of the Fisher information matrix, F

(X)

is often approximated by the identity matrix. We use

the diagonal approximation derived in (Perronnin and

Dance, 2007). Then the similarity between vectors

and G

can be deﬁned as,

(a) “China” by Sebastiao Sal-

gado.

(b) “Spain” by W. Eu-

gene Smith.

Figure 4: The most similar pair of photographs in composi-

tion style from the 8 different photographers in our dataset.

= G

′

−1

. (3)

In order to apply the Fisher kernel method, we need

to deﬁne which features are relevant to photographic

composition. Scale-invariant features (SIFT features)

have previously been shown to be useful in judging

similarity between painters (Bressan et al., 2008). We

use them as local feature vectors in our experiment.

SIFT features extract local maxima or minima from a

Gaussian pyramid as key points, and describes each

with a local histogram of orientation, which is robust

to rotation (Lowe, 2004). The features use a thresh-

olded gradient for stability under lighting adjustment.

3.2 Photographers Relationship Graph

In this section, our goal is to build a straightforward

method for visualizing the relationship amongs mas-

ter photographers. A relationship graph is constructed

according to their similarity measurements by using

multi-dimensional scaling. The more similar two

photographers are, the closer they are located on the

graph, and vice versa.

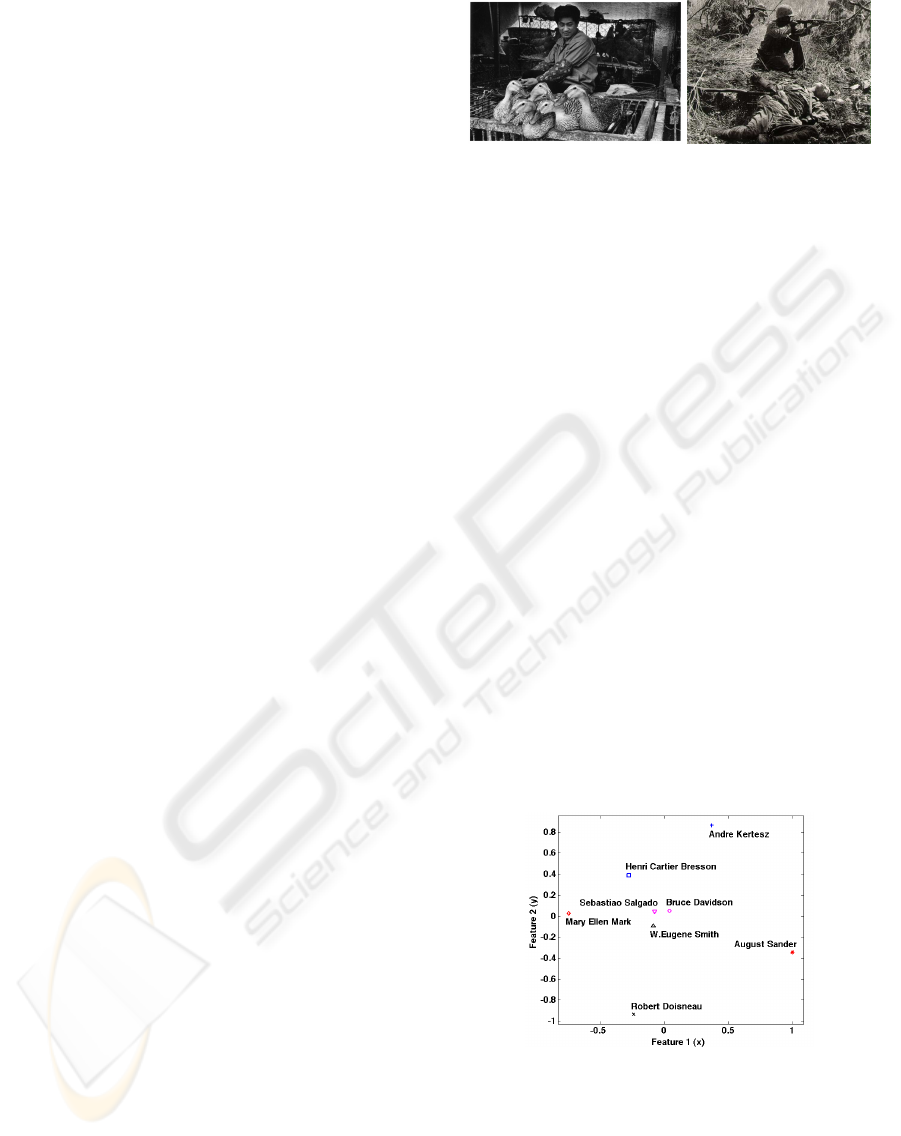
Figure 5: Photographers relationship graph, where prox-

imity indicates similarity. The photographers Doisneau,

Kertesz, Mark have distinctive styles, which agrees with

their positioning in this graph. Henri Cartier-Bresson,

whose work inﬂuenced many, is near the central locus of

Salgado, Davidson, and Smith.

Before feeding the SIFT feature vectors into

a GMM trainer (which uses the expectation-

UNDERSTANDING PHOTOGRAPHIC COMPOSITION THROUGH DATA-DRIVEN APPROACHES

427

maximization algorithm) and Fisher kernel similar-

ity measuring function, principal component analysis

(PCA) is applied to reduce the feature vector dimen-

sion. Gradient vectors are computed according to the

equation (1). Then the similarity of all the photograph

pairs in the database can be obtained by the equation

(3). Hence, a symmetric similarity matrix for pho-

tographs, denotedC, is constructed. For the similarity

of the photographers pair, we use corresponding en-

tries fromC. Given photographers A and B, their sim-

ilarity is obtained by summing all entries in C with

photographs from A and B. Obviously, the 8× 8 sim-

ilarity matrix S is also symmetric. Matrix S is nor-

malized to avoid the bias effect due to the different

number of photographs for each author.

To visualize the photographers relationship, we

applied a multidimensional scaling algorithm (van der

Heijden et al., 2004) to map the 8 photographers into

a two-dimensional space. Figure 5 shows the result.

3.3 Results and Discussions

In order to demonstrate the plausibility of using SIFT

features with Fisher kernel representations in deter-

mining composition, we exhibit the most distinctive

and most similar works that belongs to the different

photographers in Figure 3 and Figure 4. The compo-

sition of Figure 3(a) gives strong horizontal feelings

from both the long chair and the lying dancer while

Figure 3(b) gives strong vertical feelings from both

the farmer and the road. For the distribution of the

lightness, Figure 3(a) arranges the dark region in the

ceiling and relative bright regions in the other three

margins. On the contrary, Figure 3(b) arranges the

bright region in the sky and relative dark regions in

the other three margins. Studying the most similar

image pair, both Figure 4(a) and Figure 4(b) are com-

posed with the two objects in the center, where are

upright while the lower objects lie to the right side, ar-

ranged along a vertical line. The backgrounds in both

images are “messy”, which makes the foreground ob-

jects stand out. For the lightness distribution, both

photos make the lower object brighter than the upper

object and let the upper corners be relatively lighter

than the bottom corners.

Figure 5 shows the overall photographer relation-

ship graph obtained through multi-dimensional scal-

ing. Here, proximity indicates similarity. The results

show that certain photographers, such as Mary Ellen

Mark or Andre Kertesz, are “iconoclasts”. Mark is

known for challenging conventions by using oblique

view points and framing. Andre Kertesz’s composi-

tions are also distinctive, in that he organizes subjects

in triangular groupings. Similarly we can comment

(a) Gaze plot

of novice A.

(b) Gaze plot

of a novice B.

of expert A.

(d) Gaze plot

of expert B.

(e) Saliency

map of 6(a).

(f) Saliency

map of 6(b).

(g) Saliency

map of 6(c).

(h) Saliency

map of 6(d).

Figure 6: Results obtained from eye-tracking of expert pho-

tographers, and their corresponding saliency maps.

on the distinctiveness of August Sander, who tends to

put his subjects in the center, almost crowding them

in, and Robert Doisneau, whose images often con-

tain humour found in street scenes in Paris. Note also

that Henri Cartier-Bresson, a very inﬂuential photog-

rapher, appears near the center, a reasonable outcome

given that others are known to have been inﬂuenced

by him. The analysis found Sebastiao Salgado, Bruce

Davidson and W. Eugene Smith to have similar com-

position styles, which agrees with our visual exami-

nation of the photographs.

4 UNDERSTANDING WITH

BEHAVIORAL DATA

Figure 7: Spatial standard deviations of ﬁxation locations of

individual subjects. Bar 1

to bar 10

are the photographic

novice subjects and the rest are from the expert subjects.

Composition is often considered the art of guiding the

viewer’s eye. In order to understand how composi-

tion affects viewing, we used eye-tracking equipment

to examine visual ﬁxation with both novice and expert

photographers. The consistency of normal human ﬁx-

ations over an image has been investigated by Judd et

al. (Judd et al., 2009). They show that a strong bias

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

428

exists for human ﬁxations to be near the center of the

image, and also conclude that the saliency map from

one user can predict the ground truth ﬁxation of all

users remarkably well. As the ﬁxations have a strong

bias towards the center, Judd et al. show that a Gaus-

sian “blob” predicts the ground truth saliency map

reasonably well. However, they do not consider pos-

sible differences between photographic experts and

novices. We exlored this issue with our subjects.

Our experiments were carried out as follows. We

invited 10 novices and also 2 professional photogra-

phers to participate our experiments. (One of the ex-

pert photographers is a co-author of this paper.) We

set up a slide show of 30 selected photographs from

the Π database, each photograph displayed for 5 sec-

onds. The transition between photographs is ﬁlled

with 3 seconds of neutral gray image. We used a Tobii

T-60 eye-tracker to obtain the data.

4.1 The Observations of Eye Fixation

Figure 6(a) and 6(b) are the gaze plots of the novices

on the photograph ”Cowboy” by Mary Ellen Mark,

while Figure 6(c) and 6(d) are the gaze plots from

expert photographers on the same photograph. The

corresponding saliency maps are also shown in the

same columns. The saliency maps are calculated by

convolving a Gaussian kernel on the binary ﬁxation

maps, which in turn are obtained from the gaze plots

by setting the spot size radius to be the square root of

the gaze duration (milliseconds) at that location.

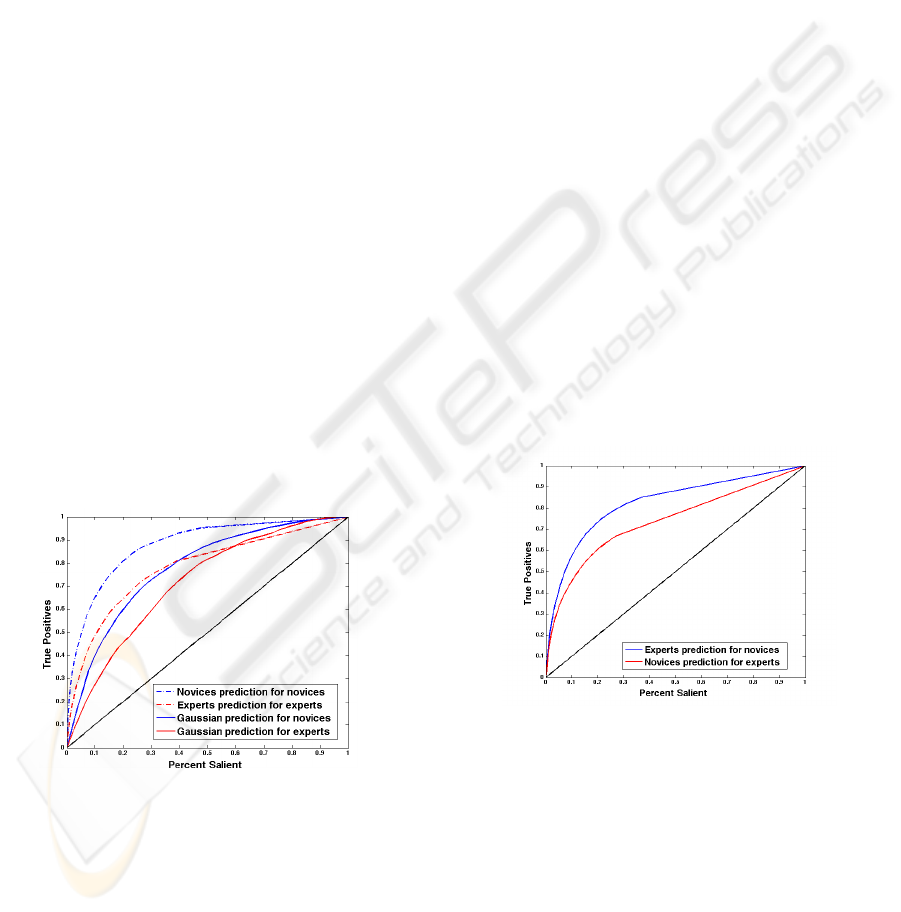
Figure 8: ROC curves for illustrating the performances of

the human prediction and Gaussian blob prediction. We see

that novices are much more consistent in gaze than experts,

and are also much better predicted by a Gaussian blob than

experts.

Observing the gaze plots, we noticed that the gaze

plot of the novice subject is typically concentrated on

the foreground object, and less likely to wander to

the background. For the experts, however, the se-

quence of gazes goes through both foreground and

background, and often wanders to the borders. For

example, they check the symmetry in the composi-

tion evident in the telephone poles around the “Cow-

boy” in the photograph. Therefore, the spatial distri-

bution of gaze plot of the novices are centralized in

the foreground region, while the gaze plots of experts

are more sparse. In the saliency maps, they have many

intersections. In particular, the pixels that have high

saliency are almost located in the same region, sug-

gesting that novices and experts could be predicted

by each other.

To check whether expert photographershave more

dispersed gaze than novices, we computed the spatial

standard deviations of ﬁxation locations over all pho-

tographs. The resuls are plotted in Figure 7. In the

chart, the 1

to 10

bars belong to novices and the

rest are from experts, showing that experts do gaze

over more of the image than novices.

4.2 Analysis of Eye Fixation Data

We analyzed the ﬁxation data obatined from novices

and experts to see what may be predicted of the two

different groups. Two kinds of predictions are studied

in this paper: human prediction and Gaussian blob

prediction. Human prediction is based on hypothesis

that each group is consistent, and the Gaussian blob

prediction is based on the hypothesis that human ﬁx-

ation is centralized on foreground objects.

Figure 9: ROC curves show that saliency map of novices

is better predicted by experts (blue curve) than vice versa

(red).

In the human prediction experiment, we treat the

saliency map from the ﬁxation locations of one user

in the group as a binary classiﬁer on every pixel in

the photograph. As in Judd et al. (Judd et al., 2009),

the saliency maps are thresholded at a level so that

a given percent of the image pixels are classiﬁed as

ﬁxated, and the rest are classiﬁed as not ﬁxated. Hu-

man ﬁxations from the other users in the same group

are ground truth ﬁxations. The threshold is varied to

sweep out an ROC curve. The x-axis of the ROC

UNDERSTANDING PHOTOGRAPHIC COMPOSITION THROUGH DATA-DRIVEN APPROACHES

429

curve is the percentage of the image pixels classiﬁed,

while the y-axis is the percentage of true ﬁxations that

are classiﬁed. We obtained the ROC for each user

in a group and averaged the results within a group.

For the Gaussian blob prediction, we take the accu-

mulated ﬁxation map of users in the group, and ﬁt it

to a circularly-symmetric two-dimensional Gaussian

distribution by matching mean and variance.

Figure 8 shows the prediction performances by the

ROC curves for the both novices and experts. The

dashed curves illustrate the human prediction perfor-

mance while the continuous curves show the Gaus-

sian blob prediction performance. Obviously, the ﬁx-

ation locations of a novice predict those of another

novice much better than one of the experts predicts

another expert. It means the eye ﬁxation of novices

has higher consistency than experts. That is per-

haps because expert photographers put their training

and experience in the appreciation of photographs,

whereas novices tend to look at the obvious in pho-

tographs. From the Gaussian blob prediction result,

we can see the ﬁxation map of novices are more cen-

tral, usually the location of foreground objects. From

the characteristics of the ROC curve, human predic-

tion performs better on novices than experts, and the

same conclusion holds for Gaussian blob prediction.

As mentioned previously, the most salient regions

of the novices usually intersect with experts’ most

salient regions. To examine that effect statistically,

we used each individual user in one group to predict

another user in the other group. The averaged inter-

group prediction ROC curves is shown in Figure 9. It

shows that the prediction of the novice ﬁxation loca-

tion by a master ﬁxation location is much better than

the prediction of a master by a novice. The result may

be understood by noting that the salient region in pho-

tograph for a novice is usually the foreground region,

while the expert considers both foreground and back-

ground regions.

5 CONCLUSIONS

This paper presents two data-driven approaches for

understanding the photographic compositions. The

ﬁrst is a feature-based method, in which we trained

a GMM model for SIFT features extracted from

monochromic photographs from master photogra-

phers. The similarity of each image pair is mea-

sured by evaluating the gradients of log-likelihood of

the GMM with weighting given by the Fisher matrix.

Then a photographers relationship graph is obtained

by using multi-dimensional scaling. In the second ap-

proach, we used gaze plots measured by eye-tracking

equipment. In that data, the prediction performanceof

both humans and Gaussian blobs are evaluated with

the help of ROC metric. We ﬁnd that eye ﬁxations

of the novices are much more consistent than those

of expert photographers, and that experts predict the

novices much better than the reverse case. In fu-

ture work, we will examine whether SIFT features

are the best for understanding composition, and study

eye-tracking with “bad” compositions by novices as

judged by experts.

REFERENCES

Bressan, M., Cifarelli, C., and Perronnin, F. (2008). An

analysis of the relationship between painters based on

their work. In ICIP, pages 113–116.

Datta, R., Joshi, D., Li, J., and Wang, J. Z. (2006). Studying

aesthetics in photographic images using a computa-

tional approach. In Proc. ECCV, pages 7–13.

Jaakkola, T. and Haussler, D. (1998). Exploiting generative

models in discriminative classiﬁers. In In Advances

in Neural Information Processing Systems 11, pages

487–493. MIT Press.

Jones-Smith, K. and Mathur, H. (2006). Fractal analysis:

Revisiting pollock’s drip paintings. Nature, pages E9–

E10.

Judd, T., Ehinger, K., Durand, F., and Torralba, A. (2009).

Learning to predict where humans look. In ICCV.

Kagian, A., Dror, G., Leyvand, T., Cohen-Or, D., and Rup-

pin, E. (2006). A humanlike predictor of facial attrac-

tiveness. In NIPS, pages 649–656.

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. International Journal of Com-

puter Vision, 60:91–110.

Lyu, S., Rockmore, D., and Farid, H. (2004). A digital tech-

nique for art authentication. Proceedings of the Na-

tional Academy of Sciences, 101(49):17006–17010.

Perronnin, F. and Dance, C. R. (2007). Fisher kernels on vi-

sual vocabularies for image categorization. In CVPR.

Taylor, R. P., Micolich, A. P., and Jonas, D. (1999). Fractal

analysis of pollock’s drip paintings. Nature, 399:422.

van der Heijden, F., Duin, R., de Ridder, D., and Tax, D.

M. J. (2004). Classiﬁcation, Parameter Estimation

and State Estimation. Wiley.

Zakia, R. (2007). Perception and imaging: photography–a

way of seeing. Elsevier Science Ltd.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

430