MULTI-CAMERA TOPOLOGY RECOVERY USING LINES

Sang Ly

, C

edric Demonceaux

and Pascal Vasseur

1,2

MIS laboratory, University of Picardie Jules Verne, 7 rue du Moulin Neuf, 80000 Amiens, France

Heudiasyc laboratory, University of Technology of Compi

egne, Centre de Recherches de Royallieu

BP 20529, 60205 Compi

egne, France

Keywords:

Multi-view reconstruction, Topology recovery, Extrinsic calibration.

Abstract:

We present a topology estimation approach for a system of single view point (SVP) cameras using lines.

Images captured by SVP cameras such as perspective, central catadioptric or ﬁsheye cameras are mapped to

spherical images using the uniﬁed projection model. We recover the topology of a multiple central camera

setup by rotation and translation decoupling. The camera rotations are ﬁrst recovered from vanishing points

of parallel lines. Next, the translations are estimated from known rotations and line projections in spherical

images. The proposed algorithm has been validated on simulated data and real images from perspective and

ﬁsheye cameras. This vision-based approach can be used to initialize an extrinsic calibration of a hybrid

camera network.

1 INTRODUCTION

Multi-camera setups, or camera networks are widely

used in vision-based surveillance activities as it pos-

sesses a larger monitoring area than a single camera.

Calibration is generally a critical step for any further

employ of the cameras. The extrinsic calibration of

a multi-camera system in order to estimate the trans-

formations (or topology) among cameras can be di-

vided into three steps: 1. feature detection and match-

ing among different views, 2. initial reconstruction

of multi-camera topology and 3. optimization of the

reconstruction using bundle adjustment. We present

in this paper a topology reconstruction approach for a

system of multiple SVP cameras which can be used in

the second step of a general calibration. We therefore

review some related works on multi-view reconstruc-

tion approaches.

Multi-view reconstruction methods can be started

with factorization technique. Tomasi and Kanade

(Tomasi and Kanade, 1992) have proposed a fac-

torization method to recover the scene structure and

camera motion from a sequence of images. The im-

plementation of this method is simple and provides

reliable results. However, its use is limited to afﬁne

camera model and it requires that all point features be

visible in all images (Hartley and Zisserman, 2003).

The projective factorization, an extension of the pre-

vious one to projective camera model, has been de-

veloped in (Sturm and Triggs, 1996; Mahamud and

M. Hebert, 2000). It is usually employed as an ini-

tialization for bundle adjustment (Triggs et al., 1999),

which should be the ﬁnal stage of any reconstruction

algorithm (Hartley and Zisserman, 2003).

Recently, L∞ optimization has been proposed to

solve the structure and motion problem. In (Kahl,

2005), Kahl has presented an L∞ approach based

on second-order cone programming (SOCP) to esti-

mate the camera translations and 3D points assuming

known rotations. Martinec and Pajdla (Martinec and

Pajdla, 2007) have solved the reconstruction problem

in two stages: estimated ﬁrst camera rotations lin-

early in least squares and then camera translations us-

ing SOCP. The main disadvantage of L∞-norm is that

it is not robust to outliers (Kahl and Hartley, 2008).

Method proposed in (Kahl, 2005) may fail due to a

single wrong correspondence (Martinec and Pajdla,

2007).

Omnidirectional vision systems possess a wider

ﬁeld of view than conventional cameras. Such de-

vices can be built up from an arrangement of sev-

eral cameras or a single camera with ﬁsheye lens or

with mirrors of particular curvatures. In structure

and motion problem, omnidirectional sensors play an

important role as they overcome several disadvan-

tages when working with perspective cameras, such

as translation/rotation ambiguity, lack of features and

the large number of views in use. In (Antone and

245

Ly S., Demonceaux C. and Vasseur P. (2010).

MULTI-CAMERA TOPOLOGY RECOVERY USING LINES.

In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 245-250

DOI: 10.5220/0002843302450250

 SciTePress

Teller, 2002), they have ﬁrst estimated camera ro-

tations using vanishing points of 3D parallel lines

and then extracted camera translations using Hough

transform. This method provided interesting results

but might be time consuming. Moreover, two stages

of their algorithm require different feature types, i.e.

lines for rotation and points for translation estima-

tions. In (Kim and Hartley, 2005), the translations

among omnidirectional cameras have been estimated

from known rotations and point correspondences us-

ing a constrained minimization.

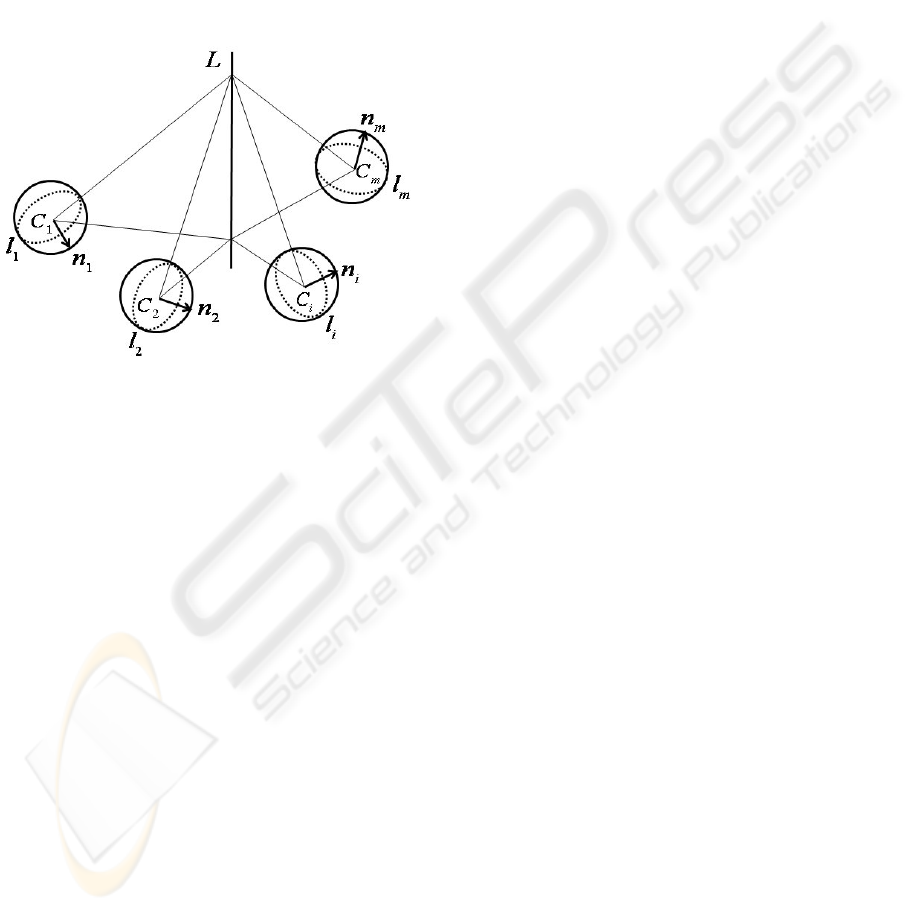
Figure 1: Multi-view geometry of spherical cameras.

In this paper, we propose a multi-view reconstruc-

tion approach in which the rotations are recovered

from bundle of parallel lines and the translations are

estimated from known rotations and line correspon-

dences across multiple views. The two main contri-

butions of this algorithm are as follows:

1. We use the uniﬁed projection model proposed by

Mei (Mei, 2007). This model encompasses a large

range of central projection devices including ﬁsh-

eye lenses. Hence, our method can be applied

to any kind of SVP cameras such as perspective,

central catadioptric and ﬁsheye cameras. We can

recover the topology of a hybrid camera network

built up from different types of central cameras.

2. Lines are used as the primitive features. Such

features are typically more stable than points and

less likely to be produced by clutter or noise, es-

pecially in man-made environment (David et al.,

2003). Compared to point features, lines are less

numerous but more informative. They have geo-

metrical and topological characteristics which are

useful for matching (Gros et al., 1998; Bay et al.,

2005). Moreover, we use uniquely lines for both

rotation and translation estimations, hence opti-

mizing the computation time of such two-stage

technique.

Our approach is slightly similar to the motion re-

covery from multi-view tensor using lines proposed

in (Gasparini and Sturm, 2008) except that we do not

need to estimate such tensors but recover directly the

transformations by decoupling rotation and transla-

tion.

In the following section, we develop the multi-

view geometry for SVP cameras. Next, we present

our topology reconstruction algorithm using lines.

We show then the experimental results from simulated

data and real images before the conclusions.

2 MULTI-VIEW GEOMETRY

Central imaging systems including ﬁsheye lenses can

be modelled by the unitary sphere, hence consid-

ered equivalent to spherical cameras. Noting that line

correspondences can be used only in more than two

views (Hartley and Zisserman, 2003), we consider a

multi-camera setup composed of at least three central

cameras. In (Torii et al., ), they demonstrated the bi-

linear and trilinear relations among spherical cameras

but did not discuss any further application. In this sec-

tion, we develop a similar trilinear relation which per-

mits the computation of multi-camera topology from

line correspondences.

Notation: Matrices are denoted using Sans Serif

fonts, vectors in bold fonts and scalars in italics.

Consider m spherical cameras with projection cen-

ters C

(i = 1,...,m) as illustrated in ﬁgure 1. A

line L in 3D space is projected to spherical images

as great circles l

with corresponding normals n

. L

can be expressed vectorially by L = X

+ µd where

L,X

,d ∈ IR

and µ ∈ IR. And n

∈ IR

are normal

correspondences in spherical images.

Let [R

] be the [Rotation|translation] between C

and the coordinate system origin O. Assuming that

is at O, we have [R

] = [I|0]. As the line L

lies on the projective planes passing through great cir-

cles l

and perpendicular to normals n

, we obtain the

next relations in which we express L in {O} and n

L + t

) = 0 (1)

Consider a triplet of views consisting of the view

1 and two other different views a and b. We denote

such triplet by (1,a,b) where 2 ≤ a,b ≤ m and a 6= b.

The trilinear relation among three views 1, a and b is

built up from equation 1 with i = 1,a,b and can be

rewritten as follows:

L = 0 (2)

where

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

246

A =









and

L = (L

,1)

The existence of at least a non-zero solution in

equation 2 requires that the 3x4 matrix A have rank

2. It results in a linear dependence among three rows

of A. Denoting A = (r

), the linear relation can

be written as r

= αr

+ βr

. Noting that r

= 0, we

can select the scalars α = kt

and β = −kt

for

some scalar k. This can be applied to the ﬁrst three

columns of A to obtain the next relation:

= αn

+ βn

(3)

= αR

+ βR

(4)

= kt

− kt

(5)

− R

+ k

1ab

= 0 (6)

with scalar k

1ab

= −1/k. Note that k is deﬁnitely

nonzero.

Equation 6 relates the normal correspondences

in a triplet of views (1,a,b) to each other through

the transformations [R

] and [R

] among those

views.

3 TOPOLOGY RECOVERY

In this section, we present our algorithm to recover

the topology of a multi-camera system by decoupling

rotations and translations.

3.1 Rotation Estimation

Rotation between two SVP cameras can be estimated

using vanishing point correspondences (Bazin et al.,

2009). We ﬁrst detect vanishing points V

(i =

1,...,m) in all views from bundles of parallel lines

and then recover all rotations R

(a = 2,...,m) using

the closed-form solution proposed by Horn in (Horn,

1987).

= R

(7)

3.2 Translation Estimation

The trilinear relation among three views 1, a and b

in equation 6 allows the estimation of translations (t

and t

) from rotations (R

and R

) and normal cor-

respondences (n

, n

and n

). With an m-camera

setup, there are C

m−1

triplets of views (1, a,b) or tri-

linear relations where C

means the number of p-

combinations from a set of q elements. These trilinear

relations can be concatenated in a single linear sys-

tem that permits the estimation of all translation t

(a = 2,...,m) from rotation R

and normal correspon-

dences n

(i = 1, ...,m).

QX = 0 (8)

where Q is a 3C

m−1

by (3m − 3 + C

m−1

) matrix as

follows:

Q = [Q

]





−R

... 0

... ... ...

0 ... −R

m−1





= diag(n

,...,n

)

X = (t

,...t

123

124

,...k

1(m−1)m

)

It can be noticed that each trilinear relation per-

mits the estimation of two translations and different

trilinear relations may contain the same translations.

However, we use all C

m−1

trilinear relations as they

are independent of each other. Obviously, from the

diagonal part Q

of matrix Q, it is impossible that a

trilinear relation is dependent on the others.

Given a line/normal correspondence n

in m spher-

ical views, equation 8 is a linear system in translations

(a = 2,...,m) and C

m−1

scalars. Each extra corre-

spondence enlarges the matrix Q by 3C

m−1

lines and

m−1

columns, and the unknown vector X by C

m−1

scalars. Therefore, n correspondences provide the fol-

lowing linear system:

X = 0 (9)

where

Q is a 3C

m−1

n by (3m−3+C

m−1

n) matrix and

X = (t

,...t

123

,...k

1(m−1)m

,...k

123

,...k

1(m−1)m

)

4 EXPERIMENTAL RESULTS

4.1 Simulated Data

Since the proposed algorithm is based on line projec-

tions in spherical images, we ﬁrst create 3D lines sur-

rounding six spherical cameras C

(i=1,...,6) with C

at the origin of the coordinate system. The average

baseline among these cameras is 2000 mm and the

3D lines are at the distance of 5000 mm to 11000 mm

from the origin. These lines are mapped to spherical

images as great circles and normals. Estimation al-

gorithm in the previous section is used to recover the

transformations among these cameras. The rotation

estimation has been already evaluated in state of the

art, therefore we focus on our translation estimation

approach.

MULTI-CAMERA TOPOLOGY RECOVERY USING LINES

247

The normals are on unitary spheres, thus may be

speciﬁed by elevation and azimuth angles. Gaussian

noise of zero mean and varying standard deviations

from 0.25 to 1.00 degrees is added to two angles of

every normal. To simulate the inaccuracy in rotation

estimation, the roll, pitch and yaw angles of each rota-

tion are perturbed by Gaussian noise of zero mean and

standard deviations from 0.25 to 1.00 degrees. Figure

2 shows the average angular error of the translation

estimation after 1000 runs.

Figure 2: Translation estimation error. Normals are per-

turbed by Gaussian noise of zero mean and standard devia-

tions of 0.25, 0.50, 0.75 and 1.00 degrees (corresponding to

4 curves).

4.2 Real Data

We show in this section the topology recovery of a

multiple SVP camera system using line projections.

In order to evaluate the topology recovery algorithm,

we have used two sets of images: one captured by a

perspective camera and the other by a ﬁsheye camera.

1. Camera calibration using the checker pattern: we

have calibrated the perspective camera using the

Camera Calibration Toolbox (Bouguet, ) and the

ﬁsheye camera using the Omnidirectional Cali-

bration Toolbox (Mei, ). The calibration provides

not only intrinsic parameters but also extrinsic

information, i.e. transformations among camera

views which is useful for the evaluation of our es-

timation.

2. Line extraction and matching: in each image set,

we have selected six images and performed the

line detection. A fast central catadioptric line

extraction method has been proposed in (Bazin

et al., 2007). The extraction is composed of a

splitting step and a merging step in both original

and spherical images. Modifying the projection

model, we extend this approach to a line detec-

tion algorithm applicable to any SVP cameras. To

focus on our estimation that requires just a few

number of line correspondences, line matching

has been done ofﬁne and manually.

3. Topology recovery from lines: we have estimated

the transformations among six camera views us-

ing our algorithm and then compared the recovery

results with the transformations provided by the

calibration in the ﬁrst step.

Figure 3: Four sample views captured by the perspective

camera with line detection and matching.

Figure 4: Two sample views captured by the ﬁsheye camera

with line detection and matching.

Figure 3 illustrates four sample views captured by

a perspective camera and ﬁgure 4 illustrates two sam-

ple views captured by a ﬁsheye camera. Line de-

tection and matching are also illustrated. Line cor-

respondences across multiple views are displayed in

same color.

The estimated rotations among perspective and

ﬁsheye views are given in tables 1 and 2 respectively

in which each rotation is represented by axis and an-

gle of rotation.

The estimation error of translations among per-

spective and ﬁsheye views is given in table 3. We have

compared the direction of each recovered translation

to the calibration data.

It can be seen from these tables that our recov-

ery algorithm provides very satisfactory results. The

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

248

Table 1: Rotation estimation for perspective views.

Recovery: Axis, Angle (deg) Error (deg)

[-0.431,-0.391,-0.813]’,51.721 0.585

[-0.998,-0.064,-0.017]’,43.846 0.174

[-0.470,0.862,-0.189]’,36.827 0.538

[0.053,-0.333,-0.942]’,167.211 0.211

[-0.0866,0.377,0.922]’,149.417 0.304

Table 2: Rotation estimation for ﬁsheye views.

Recovery: Axis, Angle (deg) Error (deg)

[-0.308,0.045,0.950]’,48.029 0.052

[-0.110,0.105,0.988]’,99.066 0.029

[0.060,0.096,0.994]’,89.702 0.114

[-0.026,-0.117,-0.993]’,131.643 0.075

[-0.477,-0.279,-0.833]’,38.405 0.023

(a)

(b)

Figure 5: (a) Topology recovery of perspective cameras -

(b) Comparison of our recovery result (in blue) and the ex-

trinsic calibration data (in red).

translation error is more signiﬁcant than the rotation

error as the translation calculation suffers from the in-

accuracy of the rotation estimation and line detection.

Table 3: Translation estimation error for perspective (sec-

ond column) and ﬁsheye (third column) views.

Error (deg)-Perspective Error (deg)-Fisheye

0.818 1.416

0.940 1.756

1.531 0.968

0.194 2.620

1.024 1.292

(a)

(b)

Figure 6: (a) Topology recovery of ﬁsheye cameras - (b)

Comparison of our recovery result (in blue) and the extrin-

sic calibration data (in red).

In ﬁgures 5 and 6 are the topology recovery of

six perspective cameras and six ﬁsheye cameras re-

spectively. We have also reconstructed the calibration

pattern. To illustrate the comparison of our topology

recovery and the extrinsic data obtained using the cal-

MULTI-CAMERA TOPOLOGY RECOVERY USING LINES

249

ibration toolbox, we display our recovery results in

blue and the extrinsic calibration results in red.

5 CONCLUSIONS

We have presented in this paper a topology recovery

approach for a setup of multiple SVP cameras. We

have validated our method using simulated data and

real images captured by perspective and ﬁsheye cam-

eras. To recovery the transformations among central

camera views, we ﬁrst estimate the rotations using

vanishing points of parallel line bundles and then the

translations from known rotations and line correspon-

dences by a linear algorithm. Using the uniﬁed pro-

jection model, this approach can be applied to a hy-

brid camera network built up from any kind of SVP

cameras. Moreover, using line feature for both rota-

tion and translation estimations, the proposed method

promises a fast transformation recovery. We have ap-

plied this method to dissimilar types of SVP cameras

and obtained very satisﬁed results. This would be a

good initial solution for a later non-linear phase such

as bundle adjustment to complete the reconstruction.

REFERENCES

M. E. Antone and S. J. Teller. Scalable extrinsic calibration

of omnidirectional image networks. In International

Journal of Computer Vision (IJCV), vol. 49, pp. 143-

174, 2002.

H. Bay, V. Ferrari and L.J. Van Gool. Wide-baseline stereo

matching with line segments. In Proc. IEEE Conf.

Computer Vision and Pattern Recognition (CVPR),

pp. 329-336, 2005.

J. C. Bazin, C. Demonceaux and P. Vasseur. Fast Cen-

tral Catadioptric Line Extraction. In 3rd Iberian Con-

ference on Pattern Recognition and Image Analysis

(IbPRIA, Lecture Notes in Computer Science, vol.

4478, pp. 25-32, 2007.

J.C. Bazin, C. Demonceaux, P. Vasseur and I.S. Kweon.

Motion estimation by decoupling rotation and trans-

lation in catadioptric vision. In Computer Vision and

Image Understanding (CVIU), 2009.

J. Y. Bouguet. Camera Calibration Toolbox for Matlab.

http://www.vision.caltech.edu/bouguetj/

P. David, D. Dementhon, R. Duraiswami and H. Samet.

Simultaneous pose and correspondence determination

using line features. In CVPR, vol. 2, pp. 424, 2003.

S. Gasparini and P. Sturm. Multi-view matching tensors

from lines for general camera models. In CVPR Work-

shops CVPRW ’08, pp. 1-6, 2008.

P. Gros, O. Bournez and E. Boyer. Using local planar ge-

ometric invariants to match and model images of line

segments. In CVIU, vol. 69, no. 2, pp. 135-155, 1998.

R. Hartley and A. Zisserman. Multiple view geometry in

computer vision. Cambridge University Press, 2nd

edition, 2003.

B. K. P. Horn. Closed-form solution of absolute orientation

using unit quaternions. In Journal of the Optical Soci-

ety of America. A, vol. 4, no. 4, pp. 629-642, 1987.

F. Kahl. Multiple view geometry and the L∞-norm. In Proc.

IEEE Int. Conf. Computer Vision (ICCV), pp. II: 1002-

1009, 2005.

F. Kahl and R. Hartley. Multiple-View Geometry Under the

∞

-Norm. In IEEE Trans. Pattern Analysis and Ma-

chine Intelligence (PAMI), vol. 30, pp. 1603-1617,

2008.

J.H. Kim and R. Hartley. Translation estimation from om-

nidirectional images. In Digital Image Computing:

Techniques and Applications (DICTA), pp. 22, 2005.

S. Mahamud and M. Hebert. Iterative projective reconstruc-

tion from multiple views. In CVPR, vol. 2, pp. 430-

437, 2000.

D. Martinec and T. Pajdla. Robust Rotation and Translation

Estimation in Multiview Reconstruction. In CVPR,

pp. 1-8, 2007.

C. Mei. Laser-augmented omnidirectional vision for 3D lo-

calisation and mapping. PhD Thesis, INRIA Sophia

Antipolis, 2007.

C. Mei. Omnidirectional Calibration Toolbox.

http://www.robots.ox.ac.uk/∼cmei/Toolbox.html

C. Olson, L. Matthies, M. Schoppers and M. Maimone. Ro-

bust stereo ego-motion for long distance navigation.

In CVPR, vol. 2, pp. 453-458, 2000.

K. Sim and R. Hartley. Recovering camera motion using the

L∞-Norm. In CVPR, pp. 1230-1237, 2006.

P. Sturm and B. Triggs. A factorization based algorithm for

multi-image projective structure and motion. In Proc.

European Conference on Computer Vision (ECCV),

pp. 709-720, 1996.

C. Tomasi and T. Kanade. Shape and motion from image

streams under orthography: a factorization method. In

IJCV(9), no. 2, pp. 137-154, 1992.

A. Torii, A. Imiya and N. Ohnishi. Two- and three- view

geometry for spherical cameras. In Proc. IEEE Work-

shop on Omnidirectional Vision (OMNIVIS05).

B. Triggs, P.F. McLauchlan, R.I. Hartley and A.W. Fitzgib-

bon. Bundle Adjustment - A Modern Synthesis. In

ICCV, pp. 298-372, 1999.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

250