A PRACTICAL APPROACH FOR APPLYING NON-LINEAR

DYNAMICS TO PARTICLE SYSTEMS

Athanasios Vogiannou, Michael G. Strintzis

Electrical & Computer Engineering Department, Aristotle University of Thessaloniki, Greece

Konstantinos Moustakas, Dimitrios Tzovaras

Informatics & Telematics Institute, Center for Research and Technology Hellas, Greece

Keywords:

Physically based modeling, Particle systems.

Abstract:

In this paper we present a new method for approximating non-linear dynamics in deformable simulations based

on a full cubic polynomial formulation of the inter-particle force. The proposed approach is a non-physical

extension of the well known St Venant Kirchhoff force, focusing on practical considerations about the behavior

of the deformable model. Therefore it is very useful for simulating and controlling non-linear stretching and

compressing properties of deformable models in applications where the computation time comprises a major

constraint. The presented force model can be easily implemented by the widely used particle systems and can

be parameterized based on a direct relation to spring models. We show that the non linear stretching behavior

of the proposed model is required for simulations where the external forces which interact with the models are

large in scale, while the performance of the presented method is comparable to simple mass-spring systems.

1 INTRODUCTION

The simulation of deformable objects has become a

signiﬁcant component of computer graphics applica-

tions for increasing the level of realism and believ-

ability of the visual outcome since textiles and elastic

objects are a major component of real environments.

An important requirement of modern simulations is

the ability to efﬁciently respond to different scales of

external forces and constraints while both the stabil-

ity of the system and the level of realism remain un-

affected (Choi and Ko, 2005; Nealen et al., 2006).

Especially in the case that strong forces are ap-

plied to the deformed objects, the material should be-

have realistically and resist further stretching with-

out collapsing. Linear spring models cannot han-

dle this kind of situations, since they allow over-

elongation and generally behave realistically only for

small deformations (Etzmuss et al., 2003). One solu-

tion would be to use springs with high stiffness val-

ues. However, this is aggravating for numerical sta-

bility and leads to less ﬂexible materials which do not

always result to the desired simulation outcome.

The physically “correct” solution to this prob-

lem would be to employ non-linear continuum mod-

els (Picinbono et al., 2003; Barbi

c and James,

2005). These models can effectively simulate materi-

als which are able to handle large deformations at the

stretch, strain and/or bend direction. However, these

models are implemented under the scheme of sophis-

ticated ﬁnite element formulations. Even though ﬁ-

nite element methods have been well established in

the computer graphics literature, they are not yet as

fast as particle systems and usually pose a signiﬁcant

degree of implementation difﬁculty to non experts in

the ﬁeld. Furthermore, they give little intuition about

the direct control over the behavior of the modeled

object, making them less appealing to animation in-

terfaces (Nealen et al., 2006).

As a consequence, the necessity of employ-

ing non-linear models with simpler implementation

schemes, such as particle systems, has recently re-

ceived the attention of researchers (Delingette, 2008;

Volino et al., 2009; Kikuuwe et al., 2009). These

methods employ continuum formulations of hyper-

elastic materials, namely the St Venant Kirchhoff ma-

terials, in order to provide realistic high performance

simulations of deformable solids or cloths.

Our work is largely motivated by this recent direc-

tion on the ﬁeld, although we focus more on practi-

Vogiannou A., G. Strintzis M., Moustakas K. and Tzovaras D. (2010).

A PRACTICAL APPROACH FOR APPLYING NON-LINEAR DYNAMICS TO PARTICLE SYSTEMS.

In Proceedings of the International Conference on Computer Graphics Theory and Applications, pages 46-53

DOI: 10.5220/0002844700460053

 SciTePress

cal considerations about the behavior of the deformed

model and deliberately ignore complex physical for-

mulations for the sake of simplicity and performance.

In particular, the proposed method is based on a

full cubic polynomial formulation of the inter-particle

force of discrete particle systems. This type of force

proves to be very useful in simulations where the ex-

ternal forces take relatively high values and therefore

non-linear stretching and compressing properties are

necessary to ensure stability and realism, both in cloth

and deformable solids simulations. We also present a

constraint based parameterization of the force which

provides a direct relation to spring models and al-

lows adjustment of the model behavior according to

practical considerations, such as the level of allowed

stretching or compression.

The paper is organized as follows: Section 2

brieﬂy discusses part of the work in the ﬁeld focusing

on particle systems and methods that connect contin-

uum models to particle systems. Section 3 describes

thoroughly the proposed method while section 4 gives

the ﬁnal details of integrating the proposed model to

particle systems. The results are presented in section

5 and the ﬁnal conclusions are drawn in section 6.

2 RELATED WORK

Since the pioneering work of Terzopoulos (Terzopou-

los et al., 1987), deformable object modeling has re-

ceived signiﬁcant attention from the computer graph-

ics community and various methods from the theory

of classical mechanics have been introduced under the

scope of graphics applications (Nealen et al., 2006;

Moore and Molloy, 2007). These methods are imple-

mented either as particle systems (Breen et al., 1994;

Baraff and Witkin, 1998; Choi and Ko, 2002; Golden-

thal et al., 2007; Selle et al., 2008; Selle et al., 2009)

or as ﬁnite elements (FE) that are based on continuum

formulations (Irving et al., 2004; Barbi

c and James,

2005; Duriez et al., 2006; Irving et al., 2007). In gen-

eral, FE methods are more accurate and robust while

particle systems are simpler to implement and usually

faster. Therefore, there is a strong effort in the ﬁeld

for combining the sophisticated properties of contin-

uum dynamics that FE methods facilitate with the

computational performance of particle systems (Etz-

muss et al., 2003; Lloyd et al., 2007).

More recently, methods for applying non lin-

ear dynamics to particle systems have been pre-

sented (Delingette, 2008; Volino et al., 2009; Kiku-

uwe et al., 2009). In particular, these methods do not

perform any linearization on the Green-Lagrange ten-

sor in the continuum model by employing St Venant

Kirchhoff (StVK) materials. Thus, they can intrin-

sically describe non-linear properties of deformable

models. In order to apply these properties along with

particle systems they proposed quite different tech-

niques. (Delingette, 2008) introduced the concept

of angular biquadratic springs for simulating mem-

branes, i.e. elastic 2D manifolds. (Volino et al., 2009)

calculate the inter-particle forces for cloths directly

from the triangle structure of the cloth manifold, in-

stead of the edge-wise approach. (Kikuuwe et al.,

2009) derived formulations that describe the inter-

particle forces on the edges of a regular tetrahedral

based volume by introducing the term of tetrahedron-

sharing edge pairs.

We also exploit the same approach to provide a

simple yet effective method for simulating and con-

trolling non-linear stretching properties of deformable

models with particle systems. In particular, we

present a network of non-linear springs, similar to

the one of (Kikuuwe et al., 2009), by introducing a

full cubic polynomial force which is formulated and

parameterized directly from practical considerations

about the model behavior. Our work can be con-

sidered as an intuitive perspective to non-linear dy-

namics that can be used directly by existing particle

systems to simulate robust and adjustable deformable

models at high performance rates.

3 PROPOSED METHOD

Non linear springs have been previously used in parti-

cle systems (Breen et al., 1994) and generally they are

reported as the natural outcome of describing forces

from non-linear strain tensors, such as the Green-

Lagrange tensor (Delingette, 2008; Kikuuwe et al.,

2009; Volino et al., 2009). In the 1D case, the force

i, j

between the particles p

and p

that corresponds

to this type of material is given by

i, j

∆x

i, j

−

∆x

i, j

(1)

where ∆x

i, j

denotes the 1D distance between the par-

ticles, L is the rest length, where the force is zero, and

K is the stiffness constant.

The above equation is a cubic polynomial de-

scribing the 1D force of StVK materials (Barbi

c and

James, 2005; Delingette, 2008; Kikuuwe et al., 2009;

Volino et al., 2009). The extension to 2D manifolds

and 3D solids is quite complex since the continuum

structure of the materials will introduce more terms

in the above force. In particular, the additional terms

correspond to the tetrahedron-sharing edge pairs and

are reported to be the major difﬁculty for extending

A PRACTICAL APPROACH FOR APPLYING NON-LINEAR DYNAMICS TO PARTICLE SYSTEMS

non linear 1D forces to higher dimensions (Kikuuwe

et al., 2009).

Even so, we can ignore any additional terms that

are induced by the continuum structure of higher di-

mensions and apply this force directly to 3D. Essen-

tially, we employ a physically based formulation only

for the behavior of the inter-particle distance |∆x

i, j

which is a 1D problem (Etzmuss et al., 2003). A par-

ticle system (or spring network) with this type of non-

linear springs has been described by (Kikuuwe et al.,

2009) as a sub-outcome of their work. The authors re-

ported that although this model does not seem to have

any physical validity, it produces similar results to the

full non-linear model while it is signiﬁcantly faster.

To our knowledge, this discrete formulation is prob-

ably the most efﬁcient, in terms of performance and

realism, non-linear mass spring system for deformed

solids in the literature.

In practice, however, there are some concerns

about the StVK force. Firstly it does not resist to

compression as does with stretching, e.g. the mate-

rial is softer under compression, while, in the case

of deformable solids, there is still the possibility of

completely collapsing (Irving et al., 2004). This is a

main limitation that made StVK generally less appeal-

ing to solid modeling. However, the recent work of

(Kikuuwe et al., 2009) showed very promising results

for large deformations of arbitrary rotation and the

proposed method can been seen as an improvement

to this approach regarding the compression problem.

Secondly these models are not reported to be eas-

ily adjusted to external requirements, e.g. 3D mod-

eling adjustments by artists or forces applied from

inside the 3D world of the simulation, and focus

mainly on accuracy (Volino et al., 2009; Delingette,

2008) or real time interaction with the deformed ob-

jects (Barbi

c and James, 2005; Volino et al., 2009).

Both drawbacks relate to the simple fact that the

StVK force is a cubic polynomial with only two

terms. A solution previously applied to this problem

was the use of a linear - Neo Hookean biphasic spring

force model (Irving et al., 2004). Although this ap-

proach solves the compression issue efﬁciently, the

pitfall is that biphasic forces need special treatment

for calculating derivatives (needed for the Jacobian)

and generally their parameterization is more complex

since two different forces are combined. In this work,

we present a more intuitive approach to solve these

issues utilizing a full cubic force on a discrete particle

system and a constraint based approach for calculat-

ing the parameters of this force. The presented force

has continuous derivatives, is simple to integrate and

parameterize and facilitates useful non-linear defor-

mation properties.

3.1 Full Cubic Force

In the rest of the text, the term force refers to the vec-

tor entity while force magnitude refers to the signed

magnitude of the force. Let the 3D vector x

denote

the position of the particle p

and again ∆x

i, j

= x

−x

Considering the force magnitude as a full cubic poly-

nomial, we can extend such expression to 3D as

i, j



a|∆x

i, j

+ b|∆x

i, j

+ c|∆x

i, j

| + d



∆x

i, j

|∆x

i, j

(2)

The parameters a, b, c and d that deﬁne the force,

and consequently the behavior of the cloth, do not

have a direct physical interpretation. In the following

section, however, we will describe a method to relate

these parameters to spring models.

The respective force derivative is given by

∂f

∂x

= I



a|∆x

i, j

+ b|∆x

i, j

| + c+

|∆x

i, j



∆x

i, j

∆x

i, j



2a+

|∆x

i, j

−

|∆x

i, j



(3)

where I denotes the 3x3 identity matrix.

3.2 Constraint based Force

Parameterization

The major problem with the intuitive step that we took

by employing a full cubic force is the calculation of

the respective parameters. In general, a set of param-

eters can de deﬁned using a corresponding system of

equations. Based on this, we can deﬁne four con-

straints on the force magnitude so that the particles

will resist to deformation.

Let g(|∆x|) denote the force magnitude as a func-

tion of the distance |∆x| between two particles, i.e.

i, j

= g(|∆x|)

∆x

|∆x|

where particle indexes are omitted for brevity.

The ﬁrst constraint should “enforce” the rest

length L of the particles by setting the force equal to

zero, i.e.

g(L) = 0 (4)

The other constraints should be related to the stiff-

ness induced by the non-linear force. In the case of

simple spring forces, the stiffness constant K deﬁnes

the ratio that the force magnitude changes according

to the deformation, i.e. the slope of the force magni-

tude - deformation curve. Thus, we can deﬁne a force

magnitude such that the stiffness increases with the

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

distance between the particle in order to resist further

elongation.

Figure 1 displays the concept. The spring force

has constant stiffness and even though this property

is good for numerical stability and performance, it

does not describe textiles well enough. The StVK

materials resist to stretching much better than simple

springs but are softer under compression. The pro-

posed approach aims at approximating the expected

deformable behavior where the internal forces resist

increasingly both to stretch and compression.

0.8 0.85 0.9 0.95 1 1.05 1.1 1.15 1.2

−2

−1

Spring

St Venant Kirchhoff

Full Cubic

Figure 1: The stiffness ratio expressed as the derivative of

the force magnitude for the spring, St Venant Kirchhoff and

the proposed (full cubic force) model. The rest length is set

to L = 1 and the spring constant to K = 1. The stiffness of

the cubic force increases with the particle distance, signiﬁ-

cantly resisting to compression and stretching compared to

the other two methods.

Based on a given spring model, we can set one

stiffness constant for the rest length and the other two

for percentages a

and a

of the rest length

′

(L) = K (5)

′

L) = K

(6)

′

L) = K

(7)

where K, K

and K

are the desired constant stiff-

ness values for different deformations rates and g

′

de-

notes the derivative of g. For example, a considerably

rational choice would be to set K

> K and K

> K

for a

= 1.1 and a

= 0.9 since, in most applications,

stretching above 10% should be avoided. In all the

parameters can be calculated by solving the follow-

ing linear system







L 1

2L 1 0

3(a

L 1 0

3(a

L 1 0































(8)

Figure 2 displays the magnitude of the proposed

force for different values of K

. In the case of stretch-

ing (i.e. |∆x| > 1) the proposed model behaves similar

to the StVK force. This is something expected since

the StVK force magnitude can be considered as a spe-

cial case of the proposed force with b = d = 0. How-

ever, in the case of compression the proposed force

increases its stiffness, compared to the StVK force

which after a certain value completely collapses. Note

also that for low deformation rates (i.e. |∆x| ≈ 1) the

full cubic force behaves similar to the linear spring

force. That is a desired feature since we usually want

to allow small deformations and resist only to large

ones.

In the case of clothes, the expected stretching

behavior is practically identical to the StVK force

model, as it had been shown by experimental re-

sults (Volino et al., 2009; Wu et al., 2003). Since the

proposed model is a good approximation of the StVK

force, it can describe sufﬁciently enough the stretch-

ing properties of cloths.

The constraints 4, 5, 6 and 7 provide a connection

between the parameters of the proposed force model

and spring forces. Using for reference a set of spring

parameters K and L, we can adjust the parameters a

, K

and K

in order to achieve the desired results,

according to practical considerations in cloth simula-

tions. In other words, the introduction of a constraint

based force parameterization provides direct manipu-

lation over the behavior of the object.

For example, models that behave like cloths have

been previously noted that should not exceed 10%

(Provot, 1995) in order to look realistic. This feature

is explicitly described by the force constraints of the

proposed method making it more suitable for adjust-

ing cloth parameters by someone with none in-depth

knowledge of mechanics, like a 3D artist. By increas-

ing or decreasing the desired deformation percentage

results in softer or stiffer materials that are, generally,

not textiles.

4 TIME INTEGRATION

Equations 2 and 3 can be applied directly to any dis-

crete model governed by the Newton’s second law of

motion f = ma. The proposed force model is em-

ployed under an implicit integration scheme as de-

scribed in (Baraff and Witkin, 1998). The implicit

solver is necessary for our approach as non-linear

forces generally result in stiffer equations and require

more stable solvers than simple linear forces. The

scheme is implemented using full evaluation of the

Jacobian (Volino et al., 2009). In our test, two itera-

A PRACTICAL APPROACH FOR APPLYING NON-LINEAR DYNAMICS TO PARTICLE SYSTEMS

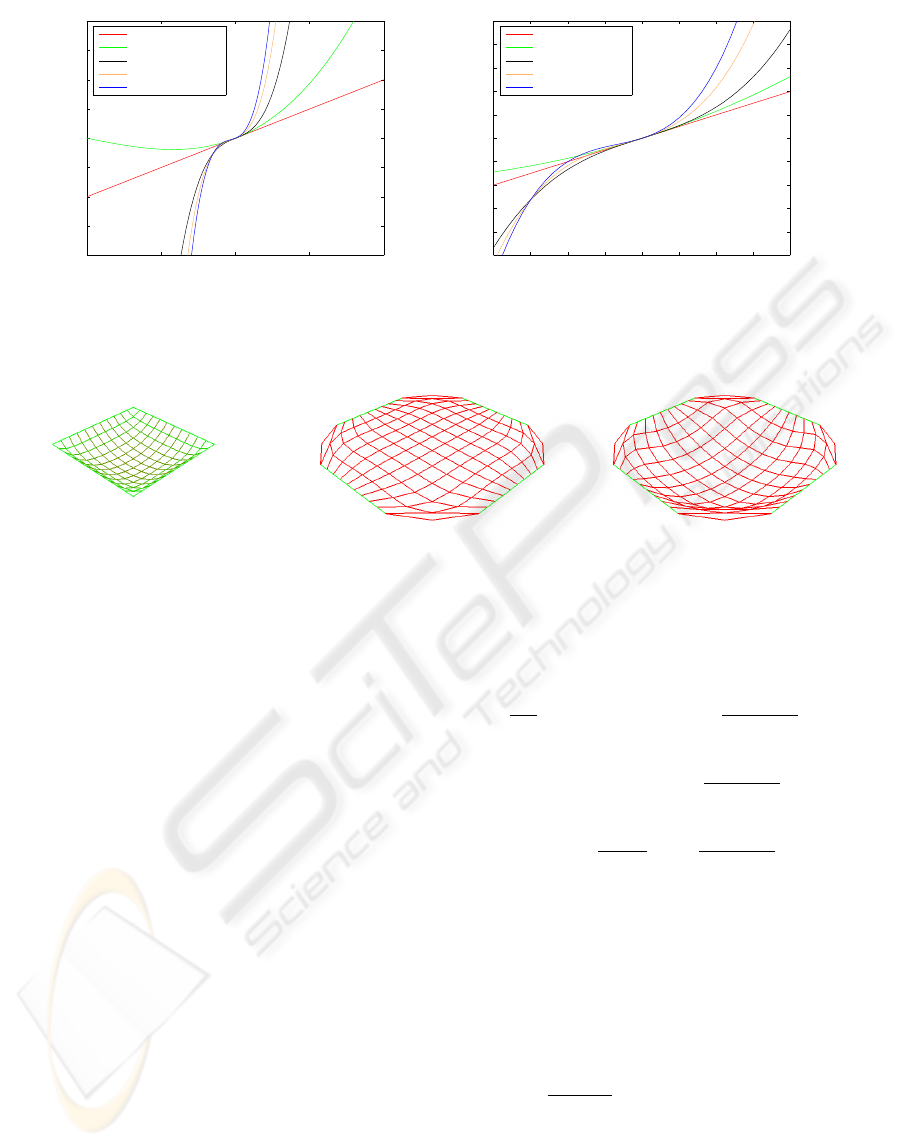
0 0.5 1 1.5 2

−2

−1.5

−1

−0.5

0.5

1.5

|Dx|

|F|

Spring

St Venant Kirchhoff

Full Cubic K1=2K

Full Cubic K1=4K

Full Cubic K1=6K

0.8 0.85 0.9 0.95 1 1.05 1.1 1.15 1.2

−0.5

−0.4

−0.3

−0.2

−0.1

0.1

0.2

0.3

0.4

0.5

|Dx|

|F|

Spring

St Venant Kirchhoff

Full Cubic K1=2K

Full Cubic K1=4K

Full Cubic K1=6K

Figure 2: Comparison of the force magnitude between spring, St. Venant Kirchhoff and the proposed (full cubic force) model.

Global view (left) and zoom (right). The rest length is L = 1 and the spring constant is K = 1. The constraint parameters for

calculating the cubic force are set to a

= 1.1, a

= 0.9, K

= 2K and K

varies for each curve (K

= 2K for black, K

= 4K

for orange and K

= 6K for blue). The proposed model can increase the resisting force at higher rates than the other models.

Figure 3: Removing out-of-plane oscillations. A low resolution lattice of particles, shown at the state resting under its

own weight(left), is signiﬁcantly stretched (effectively doubling the 2D area of the manifold) with (middle) and without the

proposed damping (right). Green lines denote lower stretching while red lines denote higher stretching. The ﬁgure on the right

shows a phase of the system oscillations, i.e. the system cannot converge to a stable state. Even though the proposed force

model is quite stable in simple draping situations, under very high stretch it is necessary to employ the proposed damping

scheme.

tions were enough for the conjugate gradient method

to converge to a physically plausible solution, just

as (Baraff and Witkin, 1998).

4.1 Damping

Damping plays a signiﬁcant role in the stability of

the numerical system (Nealen et al., 2006; Baraff and

Witkin, 1998; Schmedding et al., 2009). In general,

damping derives from both the intrinsic properties of

the modeled material and the artiﬁcial damping in-

duced by the numerical integration scheme. A sim-

ple and widely used approach is to apply a damping

force along the direction of the relative velocity be-

tween two particles (Choi and Ko, 2002; Nealen et al.,

2006; Schmedding et al., 2009). We also employ

this method in our work. However, the non-linear

properties of the full cubic force magnitude result in

high stiffness and therefore the system is sensitive to

yield undesired out-of-plane oscillations that the rela-

tive velocity damping is not guaranteed to resolve. In

particular, if we express the derivative of the force as

∂f

∂x

= Ic+a|∆x

i, j

I+ 2

∆x

i, j

∆x

i, j

∆x

i, j

∆x

i, j

b|∆x

i, j

I+

∆x

i, j

∆x

i, j

∆x

i, j

∆x

i, j

|∆x

i, j

I−

∆x

i, j

∆x

i, j

∆x

i, j

∆x

i, j

(9)

we can distinguish between the effect of each pa-

rameter a, b, c and d to the Jacobian. In general, pa-

rameters with negative values may introduce negative

eigenvalues in the system that will affect stability.

Solving the linear system (8) for the four param-

eters, b and d take negative values (considering that

K < K

, K < K

and L, a

, a

take positive val-

ues). Especially in the case of parameter d, the

term



I−

∆x

i, j

∆x

i, j

∆x

i, j

∆x

i, j



expresses stiffness orthogonal

to the interaction direction, i.e. out-of-plane direc-

tion, which is something that can cause problems in

simulations (Choi and Ko, 2002).

In previous approaches, terms that end up to nega-

tive eigenvalues (such as the two last terms of the right

part of equation 9) were either disregarded (Volino

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

and Thalmann, 2000; Choi and Ko, 2002) or their ef-

fect was reduced using specially designed damping

forces (Baraff and Witkin, 1998). Completely disre-

garding these terms resulted in excessively resisting

to bending in our simulations. Instead of this, we re-

duced, by a small percentage, the absolute values of

the parameters b and d only in the calculation of the

Jacobian (effectively “damping” speciﬁc terms of the

Jacobian). This way we can avoid adding more forces

in our scheme and effectively reduce out-of-plane os-

cillations.

Figure 3 shows an example of a particle system

with and without the proposed damping. The system

is ﬁxed on the edges and is left draping under its own

weight. By moving further the ﬁxed edges, the sys-

tem is stretched reaching to a ﬁnal position that is al-

most twice the the size of the textile at its rest state.

This excessive stretching generates high valued inter-

particle forces that also “stretch” the numerical solver

(in the draping state, i.e. low stretch, the force val-

ues are close to the ones of a simple linear spring and

no safe conclusions can be drawn about the stability

of the proposed force). When the proposed damping

scheme is not used, the system cannot converge to a

stable state and oscillates in the out-of-plane direction

(Figure 3 right). If we reduce the parameters b and d

to 99% of their absolutes values in the calculation of

the Jacobian then the system performs robustly and

converges to a stable stretched state (Figure 3 mid-

dle).

Note that a consequence of this kind of damping

is that it artiﬁcially dissipates energy from the system

and resists to bending (Volino and Thalmann, 2000;

Choi and Ko, 2002; Baraff and Witkin, 1998). Even

so, it is still possible to ignore it in applications that

high stretching is not directly applied to the particle

system without affecting the stability of the system.

5 EXPERIMENTAL RESULTS

We have tested the proposed method in technical sim-

ulations, both with solids and textiles, that involve

high scales of forces applied to the deformed ma-

terials, yet these forces are generated directly from

conditions of the virtual worlds. We also evaluated

the effect of the constraint parameters (section 3.2)

to the behavior of the cloth under simple draping.

The whole experimental setup was implemented us-

ing C++ on a Core2 6600 2,4GHz CPU PC with 2GB

of RAM and a GeForce 7600 GS Graphics Card.

For comparison we have also implemented: 1)

a simple linear model, 2) the StVK triangle based

method described in (Volino et al., 2009) (we refer

Figure 4: A heavy ball falling into a cloth. The weight of

the ball is 10 kg, effectively 10 times the total weight of

the cloth. The particle system consists of 1024 and the pa-

rameters of the system are: L = 2cm, a

= 1.04, a

= 0.96,

K = 1000N/m, K

= 6K, K

= 2K. The proposed method

can robustly handle the heavy ball (left) while a mass-spring

system set to the same base stiffness K allows unrealistic

over-elongation of the cloth (right). Testing larger values of

K led to partially or totally unstable simulations.

Figure 5: A heavy cube hanging from a cloth. The weight of

the cube is 5 kg, effectively 5 times the weight of the cloth.

The rest of the parameters are set to L = 2cm, K = 500N/m,

= 1.1, a

= 0.9, K

= 2K, K

= 6K. Again, testing larger

values of K led to partially or totally unstable simulations.

Figure 6: Deformable cube simulation composed of 729

particles. The cube can react robustly both under low defor-

mation (left), such as linear models do, but can also resist

to high compression (right). In this test (right) neither the

linear or the StVK models managed to resist compression

and completely collapsed, resulting in unacceptable visual

outcome. The cube weight was 5kg which is almost 7 times

the mass of the deformed cube. The rest of the parameters

are: L = 2cm, K = 1000N/m, a

= 1.1, a

= 0.9, K

= 10K,

= 6K.

A PRACTICAL APPROACH FOR APPLYING NON-LINEAR DYNAMICS TO PARTICLE SYSTEMS

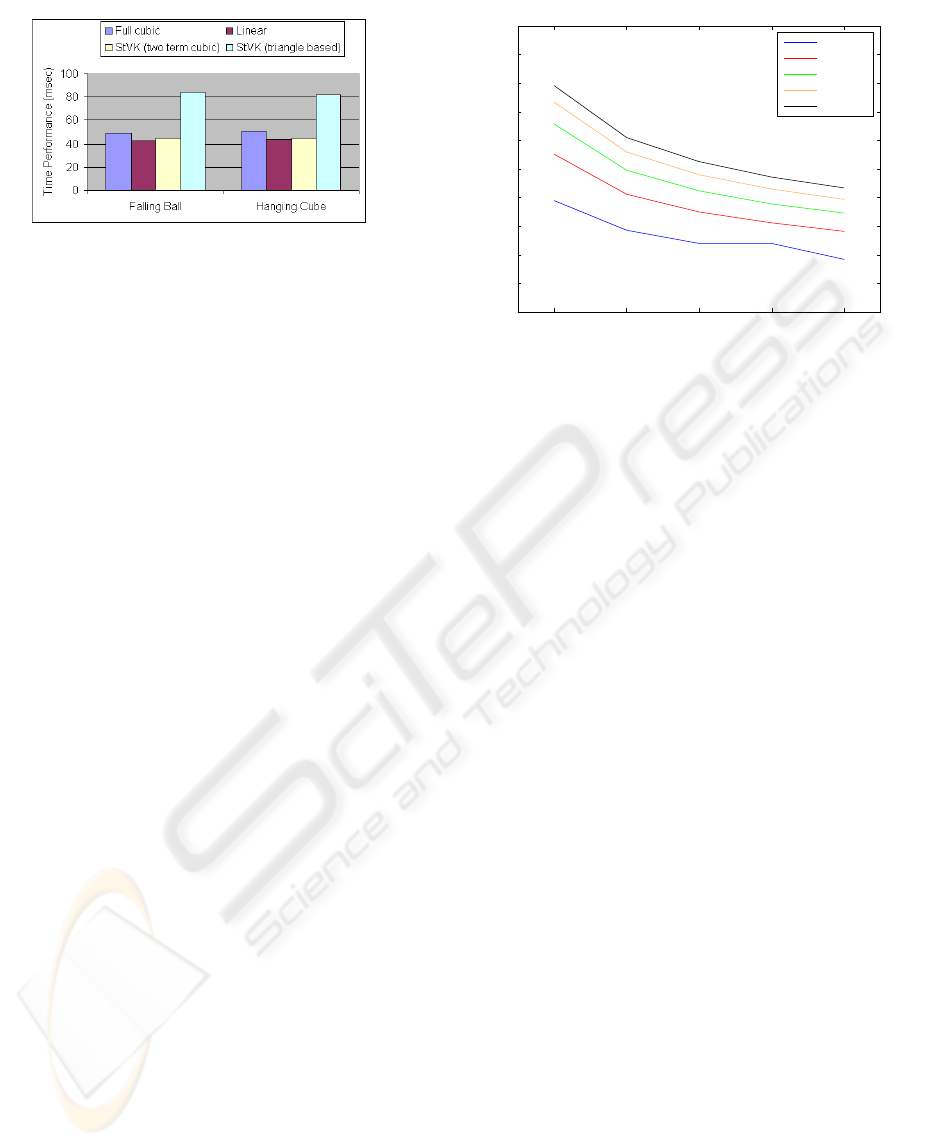
Figure 7: Timing Performance of the compared methods.

The StVK (two term cubic) model refers to method of

(Kikuuwe et al., 2009) while the StVK (triangle based)

refers to the one of (Volino et al., 2009). The proposed

method is insigniﬁcantly slower (10%) than the linear and

the two term cubic models while it is considerably faster

(40%) than the triangle based StVK.

to it as triangle based because the calculations re-

quire knowledge of the triangle structure of the mesh)

and 3) the spring network of (Kikuuwe et al., 2009),

which essentially employs a cubic force with two

terms. Methods 1 and 3 were tested in all simulations

while method 2 was tested only in cloth simulations

since it is specialy described for these purposes. We

have not compared with any full FEM method since

recent results of (Kikuuwe et al., 2009) showed that

method 3 is much faster than full FE implementa-

tions. Note also that this comparison is performed

under the scope of a general evaluation of the results,

since none of these works speciﬁcally aimed at sim-

ulating adaptive models that resist high value forces.

To our knowledge, they are not any methods in the

literature that have dealt with this particular problem.

Figure 4 shows a heavy ball falling into the surface

of a cloth. The proposed force model allows small de-

formations of the cloth so that it looks loose (and not

stiff) while can also resist to the weight of the ball. A

linear force which allows the same level of small de-

formation is unable to realistically hold the ball. Fig-

ure 5 illustrates a similar example where one edge of

a cloth is connected to a heavy cube while the other

one is ﬁxed. Again the proposed approach manages

to resist over-elongation compared to a linear model

with the same parameters.

Figure 6 shows an example of a deformable solid

cube modeled by a particle system and the proposed

force. The proposed method is able to react both to

small deformations, like the interactive stretching dis-

played in the left image, and also resist the compres-

sion caused by the heavy cube. The linear model re-

sulted in similar behavior for small deformation but

completely collapsed under compression. Likewise,

while in both cloth applications the StVK methods

produced similar results with the proposed method

2 4 6 8 10

0.005

0.01

0.015

0.02

0.025

0.03

0.035

0.04

0.045

0.05

K1 (multiples of K)

Average Stretch Ratio

a1=0.02

a1=0.04

a1=0.06

a1=0.08

a1=0.1

Figure 8: Deformation rates for different constraint param-

eters. For testing stretching, we measured the average de-

formation ratio of a cloth with one edge ﬁxed draping under

its own weight. The results show that we can achieve sim-

ilar results with a different combination of the parameters,

thus the proposed constraint based parameterization is very

adaptive to application requirements.

(allowing a bit more elongation which did not af-

fect much the level of realism however), we could

not produce a visually acceptable result using the

two-term StVK force of (Kikuuwe et al., 2009) (the

triangle-based StVK does not apply directly to solids)

since StVK materials are softer under compression

and eventually collapse due to the weight of the heavy

cube.

In ﬁgure 7 we display the comparative timing re-

sults for the two cloth applications. The timing cal-

culations include the calculation of the force values,

the calculation of the Jacobian and the iterations of

the Conjugate Gradient. The proposed method is ap-

proximately 5-10% slower than the linear model and

(Kikuuwe et al., 2009) which is something expected

since these models employ computationally simpler

forces. However, note that the linear method failed in

all simulations, (Kikuuwe et al., 2009) failed in the

compression of the deformed solid and the time dif-

ference is not so signiﬁcant. Compared to the contin-

uum based StVK of (Volino et al., 2009), the proposed

method is approximately 40% faster.

In the last ﬁgure 8 we display the average defor-

mation rate of a cloth according to different constraint

parameters. The cloth was simply left draping under

its own weight until it stopped. The diagram shows

that the proposed model can effectively produce sim-

ilar deformation ratios with various combinations of

the constraints.

This allows the user to adjust the parameters ac-

cording to the restrictions imposed from different

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

parts of the application. For example, if large val-

ues of K are not desired but the average stretch ratio

should remain at a low level (e.g. solids that practi-

cally keep their volume but have soft surface), then a

lower value for a

can achieve the desired result with-

out this increase in stiffness K.

6 CONCLUSIONS

In this paper we presented a particle system that uti-

lizes a full cubic formulation of the inter-particle force

to apply non-linear deformation resistance to simula-

tion conditions of high scale. We also introduced a

constraint based force parameterization for adjusting

the proposed force and described the details regarding

the necessary damping that the presented non-linear

scheme requires in order to ensure numerical stability.

The proposed method is conceptually simple to im-

plement and parameterize according to practical con-

siderations. We showed that the presented method can

robustly handle deformable models that are subject to

environment forces of high scale, both for stretching

and compression. Since the presented force is imple-

mented with particle systems, it has very efﬁcient tim-

ing performance, comparable to simple linear models.

REFERENCES

Baraff, D. and Witkin, A. (1998). Large steps in cloth sim-

ulation. In SIGGRAPH ’98, pages 43–54.

Barbi

c, J. and James, D. L. (2005). Real-time subspace inte-

gration for St. Venant-Kirchhoff deformable models.

ACM Transactions on Graphics (SIGGRAPH 2005),

24(3):982–990.

Breen, D. E., House, D. H., and Wozny, M. J. (1994). Pre-

dicting the drape of woven cloth using interacting par-

ticles. In SIGGRAPH ’94, pages 365–372.

Choi, K.-J. and Ko, H.-S. (2002). Stable but responsive

cloth. ACM Trans. Graph., 21(3):604–611.

Choi, K.-J. and Ko, H.-S. (2005). Research problems

in clothing simulation. Computer-Aided Design,

37:585–592.

Delingette, H. (2008). Triangular springs for modeling non-

linear membranes. IEEE Transactions on Visualiza-

tion and Computer Graphics, 14(2):329–341.

Duriez, C., Dubois, F., Kheddar, A., and Andriot, C. (2006).

Realistic haptic rendering of interacting deformable

objects in virtual environments. IEEE Transactions on

Visualization and Computer Graphics, 12(1):36–47.

Etzmuss, O., Gross, J., and Strasser, W. (2003). Deriving

a particle system from continuum mechanics for the

animation of deformable objects. IEEE Transactions

on Visualization and Computer Graphics, 9(4):538–

550.

Goldenthal, R., Harmon, D., Fattal, R., Bercovier, M., and

Grinspun, E. (2007). Efﬁcient simulation of inexten-

sible cloth. ACM Transactions on Graphics (Proceed-

ings of SIGGRAPH 2007), 26(3).

Irving, G., Schroeder, C., and Fedkiw, R. (2007). Volume

conserving ﬁnite element simulations of deformable

models. In SIGGRAPH ’07, page 13.

Irving, G., Teran, J., and Fedkiw, R. (2004). Invertible ﬁ-

nite elements for robust simulation of large deforma-

tion. In ACM SIGGRAPH/Eurographics symposium

on Computer animation, pages 131–140.

Kikuuwe, R., Tabuchi, H., and Yamamoto, M. (2009).

An edge-based computationally efﬁcient formulation

of saint venant-kirchhoff tetrahedral ﬁnite elements.

ACM Trans. Graph., 28(1):1–13.

Lloyd, B., Szekely, G., and Harders, M. (2007). Identiﬁca-

tion of spring parameters for deformable object simu-

lation. IEEE Transactions on Visualization and Com-

puter Graphics, 13(5):1081–1094.

Moore, P. and Molloy, D. (2007). A survey of computer-

based deformable models. In IMVIP ’07: Proceed-

ings of the International Machine Vision and Image

Processing Conference, pages 55–66.

Nealen, A., Mueller, M., Keiser, R., Boxerman, E., and

Carlson, M. (2006). Physically based deformable

models in computer graphics. Computer Graphics Fo-

rum, 25(4):809–836.

Picinbono, G., Delingette, H., and Ayache, N. (2003). Non-

linear anisotropic elasticity for real-time surgery sim-

ulation. Graph. Models, 65(5):305–321.

Provot, X. (1995). Deformation constraints in a mass-spring

model to describe rigid cloth behavior. In Graphics

Interface ’95, pages 147–154.

Schmedding, R., Gissler, M., and Teschner, M. (2009). Op-

timized damping for dynamic simulations. In Spring

Conference on Computer Graphics, Budmerice, Slo-

vakia, pages 205–212.

Selle, A., Lentine, M., and Fedkiw, R. (2008). A mass

spring model for hair simulation. ACM Trans. Graph.,

27(3):1–11.

Selle, A., Su, J., Irving, G., and Fedkiw, R. (2009). Robust

high-resolution cloth using parallelism, history-based

collisions, and accurate friction. IEEE Transactions

on Visualization and Computer Graphics, 15(2):339–

350.

Terzopoulos, D., Platt, J., Barr, A., and Fleischer, K. (1987).

Elastically deformable models. In SIGGRAPH ’87,

pages 205–214.

Volino, P., Faure, F., and Magnenat-Thalmann, N. (2009).

Simple, yet accurate tensile stiffness. ACM Trans.

Graph., 28(4).

Volino, P. and Thalmann, N. M. (2000). Implementing fast

cloth simulation with collision response. In CGI ’00:

Proceedings of the International Conference on Com-

puter Graphics, page 257.

Wu, Z., Au, C., and Yuen, M. (2003). Mechanical proper-

ties of fabric materials for draping simulation. Inter-

national Journal of Clothing Science and Technology,

15(1):56–68.

A PRACTICAL APPROACH FOR APPLYING NON-LINEAR DYNAMICS TO PARTICLE SYSTEMS