
CONTOUR SEGMENT ANALYSIS
FOR HUMAN SILHOUETTE PRE-SEGMENTATION
Cyrille Migniot, Pascal Bertolino and Jean-Marc Chassery
CNRS Gipsa-Lab DIS, 961 rue de la Houille Blanche BP 46 - 38402 Grenoble Cedex, France
Keywords:
Human detection and segmentation, Silhouette, Histograms of oriented gradients.
Abstract:
Human detection and segmentation is a challenging task owing to variations in human pose and clothing. The
union of Histograms of Oriented Gradients based descriptors and of a Support Vector Machine classifier is
a classic and efficient method for human detection in the images. Conversely, as often in detection, accurate
segmentation of these persons is not performed. Many applications however need it. This paper tackles the
problem of giving rise to information that will guide the final segmentation step. It presents a method which
uses the union mention above to relate to each contour segment a likelihood degree of being part of a human
silhouette. Thus, data previously computed in detection are used in the pre-segmentation. A human silhouette
database was ceated for learning.
1 INTRODUCTION
Simultaneous detection and segmentation of element
of a known class , and in particular with the one of
persons, is a much discussed problem. Due to the var-
ious colors and positions that a person can have, it is
a challenging task. The aim is to avoid user supervi-
sion. It is a critical part in any applications such as
video surveillance, driver-assistance or video index-
ing.
Dalal (Dalal and Triggs, 2005) presented an efficient
and reliable detection algorithm based on Histograms
of Oriented Gradient (HOG) descriptors with Support
Vector Machine classifier. Nevertheless, if person lo-
calization is performed, no information about his/her
shape is provided and segmentation is not done.
This paper describes a HOG local process. Indeed
HOG global process in a detection window makes a
decision about the presence of a person in the win-
dow. With HOG local process, information relied on
the person silhouette is obtained. Our method uses
this approach in order to determine the relevance as a
person silhouette part for each contour segment (Fig-
ure 1). This data might allow segmentation, for exam-
ple by looking for the shortest-path cycle in a graph.
Here, contour segments are an interesting support.
Given that only shape is discriminative of person
class, it is logical to study contours. Furthermore,
segments gather pixels that share the same location
and orientation. Associating them with HOGs based
results is therefore relevant and permits to re-use data
computed during detection.
Our method studies a positive detection window (con-
taining a person) and generates for each contour
segment a human silhouette membership likelihood
value. Learning and tests are made with the IN-
RIA Static Person Data Set containing positive detec-
tion windows of Dalal’s algorithm (Dalal and Triggs,
2005).
Figure 1: Input image (a), contour image computed with
Canny algorithm (b), contour pixels gathered in contour
segments (c) and likely segments (d).
1.1 Related Work
Most human detection works have used a “descrip-
tor/classifier” framework (Figure 2). The descriptor
converts an image into a vector of discriminative fea-
tures of the searched class. The classifier, from an
image feature vector, determines whether a person
is in the image. To describe a class, the classifier
74
Migniot C., Bertolino P. and Chassery J. (2010).
CONTOUR SEGMENT ANALYSIS FOR HUMAN SILHOUETTE PRE-SEGMENTATION.
In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 74-80
DOI: 10.5220/0002845300740080
Copyright
c
SciTePress

is made from feature vectors of positive (containing
an instance of the target class) and negative detection
windows. SVM (Vapnik, 1995), AdaBoost (Freund
Figure 2: The “descriptor/classifier” framework principle.
and Schapire, 1995) and neural networks (Toth and
Aach, 2003) are the most used classifiers. Regard-
ing descriptors, Haar wavelets (Oren et al., 1997) and
HOGs are the most usual but Principal Component
Analysis (PCA) (Munder et al., 2008), Riemannian
manifold (Tuzel et al., 2007) or Fourier descriptors
(Toth and Aach, 2003) are used too. Detection can
be done for the entire person or for body parts (limbs,
torso, head, etc.) as in (Alonso et al., 2007). Never-
theless, other works are based on other techniques as,
for example, human movement recognition and par-
ticularly walking periodicity (Ran et al., 2005).
Simultaneous detection and segmentation need other
processing. Using stereo (Kang et al., 2002) easily
gives a segmentation of elements of different depths
but requires particular equipment. Silhouette template
matching (Lin et al., 2007) (Munder and Gavrila,
2006) allows segmentation with the nearest known
template.
Contour segments analysis is used as well. (Wu and
Nevatia, 2007) captures most important edgelets with
a cascade of classifiers but essentially for detection.
(Sharma and Davis, 2007) looks for the most likely
contour segment cycles without any knowledge on the
studied class. These cycles are attached to some per-
son features, using a Markov random field. This is an
approach inverse to ours.
1.2 HOG and SVM Combination
Our method is based on the combination used by
(Dalal and Triggs, 2005) for detection, as we remind
in this section. The process consists in testing all pos-
sible detection windows for all locations and scales.
A human presence measure is associated to each de-
tection window.
Descriptors are based on contour orientation. In order
to obtain spatial informations, any studied detection
window is divided into areas named blocks and cells.
1.2.1 Blocks and Cells
The detection window is divided by a rectangular
grid. Cells are integrated into blocks. Each block con-
tains a fixed number of cells. Each cell belongs to at
least one block.
Without block overlapping, a cell belongs to a single
block. Division into blocks is also performed using a
rectangular grid (Figure 3). With block overlapping,
a cell may belong to several blocks. First, we do not
use block overlapping.
Figure 3: Image partitioned in blocks (in red) and cells (in
blue) with no block overlapping.
1.2.2 Histograms of Oriented Gradients
For a given area, a HOG means the proportion of con-
tour pixels for each orientation bin. Orientation inter-
val is evenly divided in N
bin
orientation bins in ∆:
∆ =
I
k
=
2k− 1
2N
bin
π,
2k+ 1
2N
bin
π
, k ∈ [1, N
bin
]
(1)
Let ν
cell
I
be the occurrence frequency of contour pix-
els whose orientation belongs to interval I in the cell
cell. The cell HOG is given by:
HOG
cell
=
n
ν
cell
I
, I ∈ ∆
o
(2)
1.2.3 Descriptor
HOGs are descriptors and thus are described by fea-
ture vectors. Clothe colors and texture variations are
not discriminative. HOGs describe shape and are also
relevant for human detection.
1.2.4 Classifier
For a block block, the feature vector V
block
is made
from all HOGs of its cells:
V
block
= {HOG
cell
, cell ∈ block} (3)
With the normed concatenated vector of the feature
vectors of all blocks, the SVM classifier indicates
whether a person is in the detection window. An
overview of the method is shown in Figure 4.
CONTOUR SEGMENT ANALYSIS FOR HUMAN SILHOUETTE PRE-SEGMENTATION
75
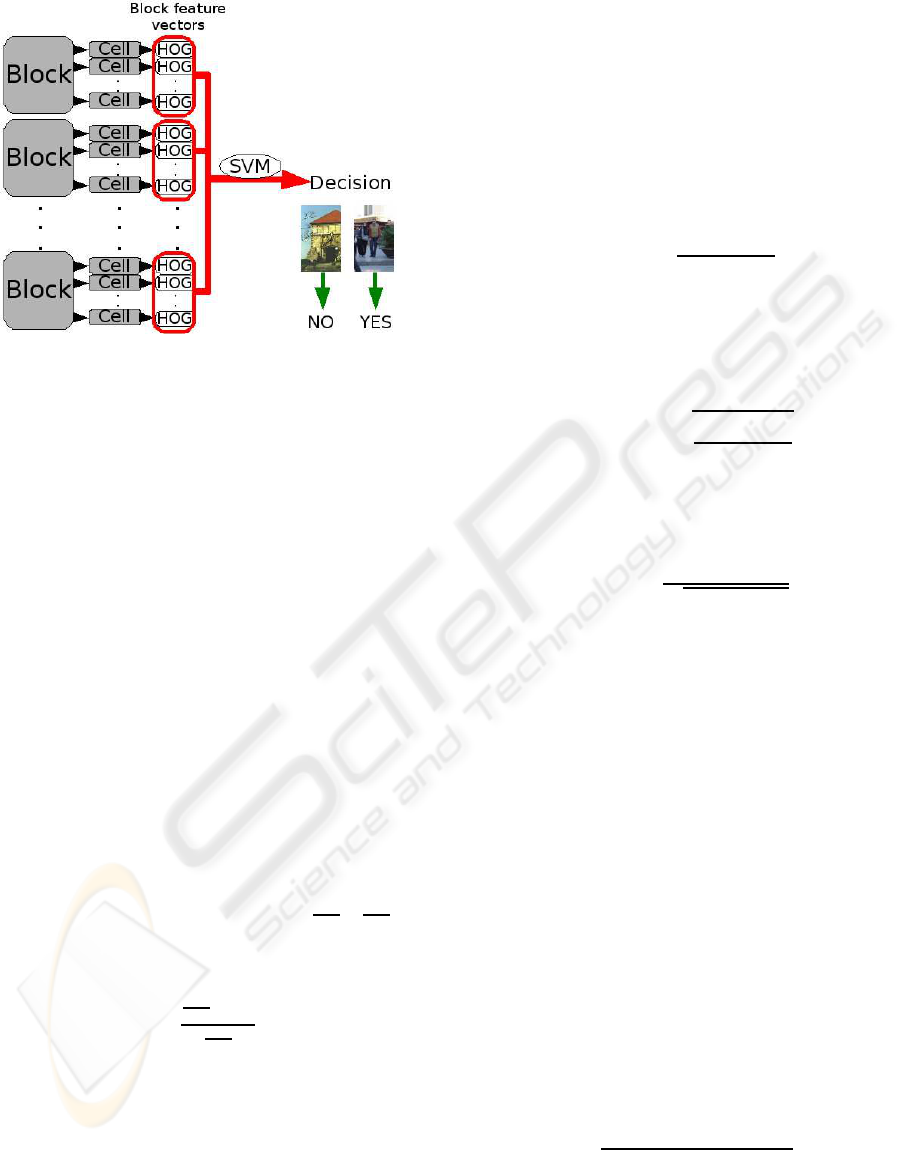
Figure 4: An overview of person detection.
2 COMBINING HOG WITH SVM
FOR EACH BLOCK
In our approach, the classification process is not any-
more performed globally but at the block level in or-
der to classify any piece of contour has being or not a
piece of the person’s silhouette. First, a contour map
of the detection window is computed using the Canny
algorithm. Then a list of contour segment is created.
The window is divided into blocks and cells. In the
following, we present the method without then with
block overlapping.
2.1 Without Block Overlapping
The method shown previously provides a value for
each window. Our aim is to have one for each con-
tour segment.
2.1.1 Feature Vectors
Each contour pixel with orientation θ ∈
h
k
N
bin
π,
k+1
N
bin
π
i
updates two bins of the cell’s HOG with weights ω
(for bin ν
I
k
) and 1− ω (for bin ν
I
k+1
) as follows:
ω =
k+1
N
bin
π− θ
π
N
bin
(4)
HOG
cell
are still obtained with equation 2 and V
block
with equation 3.
For segment likelihood calculation, HOG block is de-
fined by:
HOG
block
=
n
ν
block
I
, I ∈ ∆
o
(5)
2.1.2 Normalization
Illumination and contrast can greatly modify HOG
values. This leads to a reduction of the efficiency in
the learning and classification process. Thus a nor-
malization of V
block
is performed. Let N be the vec-
tor size. Four different normalization schemes were
tested:
• L1-norm: averaging by the norm L1 of the vector:
V
L1
bloc
(i) =
V
block
(i)
N
∑
k=1
V
block
(k)
(6)
• L1sqrt norm: the square root of the L1-norm is
used to express the feature vector as a probability
distribution
V
L1
sqrt
bloc
(i) =
v
u
u
u
u
t
V
block
(i)
N
∑
k=1
V
block
(k)
(7)
• L2-norm: averaging by the norm L2 of the vector:
V
L2
bloc
(i) =
V
block
(i)
s
N
∑
k=1
V
block
(k)
2
(8)
• L2-Hyst norm: non linear illumination variations
could make saturations in the acquisition and
cause sharp magnitude variations. High magni-
tude gradient influence is here decreased by ap-
plying a threshold of 0.2 after L2-normalization.
Finally L1-normalization is performed.
These norms effects are shown in section 3.
2.1.3 Likely Segments
From the database examples, SVM constructs a hy-
perplane to separate positive and negative elements.
Algebraic distance between an example and this hy-
perplane provides the classification and associates to
each block a value S
SVM
block
. An overview is shown in
Figure 5. For contour segment seg with orientation
θ ∈ I , let t
b
k
be this segment pixel count belonging to
block b
k
. In a windowcontaining N
b
blocks, the value
associated to this segment is:
P
seg
=
∑
N
b
k=1
t
b
k
HOG
b
k
(I )S
SVM
b
k
∑
N
b
k=1
t
b
k
(9)
This value is the likelihood of a segment to be part of
a human silhouette.
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
76
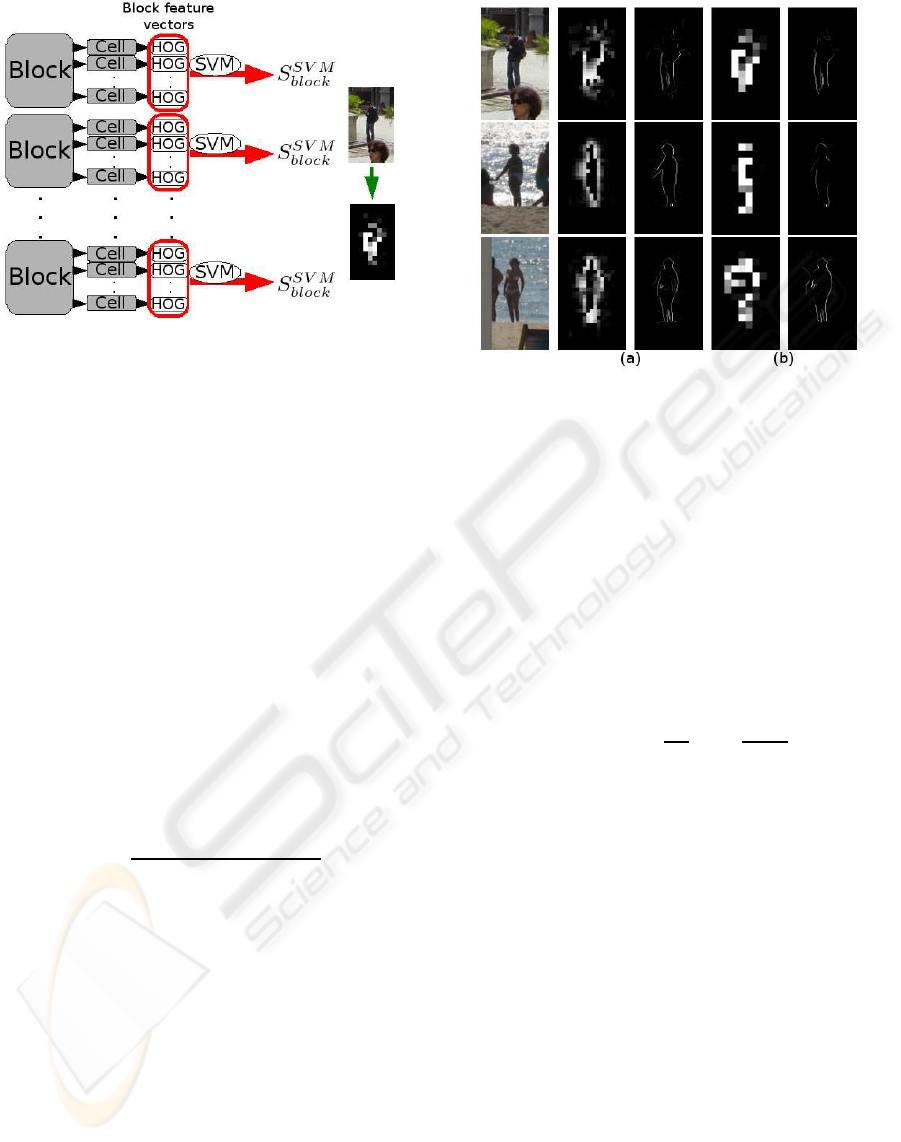
Figure 5: An overview of our approach.
2.2 With Block Overlapping
An important number of cells in a block leads to an
efficient descriptor. An important number of blocks
gives more spatially accurate results. Nevertheless
cells with too small size is not informative enough.
The solution is block overlapping. A cell could be-
long to several blocks. Hence, cell number and size
could be higher than previously.
In practice, in SVM output, a value S
SVM
block
is al-
ways allocated to each block. But, since a single cell
can belong to several blocks, a value S
SVM
cell
is associ-
ated with each cell.
S
SVM
cell
= mean
bloc∋cell
(S
SVM
block
) (10)
For a contour segment seg with orientation θ ∈ I , let
t
c
k
be segment pixel count belonging to cell c
k
. In a
window containing N
c
cells, the value associated with
this segment is:
P
rec
seg
=
∑
N
c
k=1
t
c
k
HOG
c
k
(I )S
SVM
c
k
∑
N
c
k=1
t
c
k
(11)
3 RESULTS
To evaluate the ability of our method to extract in-
formation about person silhouette, we tested it on
INRIA Static Person Data Set consisting of images
of person in various upright poses. Learning is re-
alized with 200 binary silhouette images obtained
from positive examples and 200 negative examples.
This database is available from http://www.gipsa-
lab.inpg.fr/∼cyrille.migniot/recherches.html. SVM-
light algorithm (Joachims, 1999) is used as classifier.
In Figure 6 and 10, each block (or cell) is colored
with a gray level proportionalto its SVM output (then,
each segment). Contrary to other methods, a non bi-
Figure 6: Effects of block overlapping: SVM outputs and
likely segments with block overlapping (a) and same results
without block overlapping (b).
nary value is associated to each segment. Thus, evalu-
ation of the method also needs a new benchmark that
is decribed in the following. For a positive detection
window pdw, let M
pdw
pos
be the mean of P values as-
sociated to segment’s pixels belonging to human sil-
houette and M
pdw
neg
the mean of P values associated to
other segment’s pixels.
Let benchmark be a value relative to our method per-
formance, computed from N
w
detection windows as
follows:
benchmark =
1
N
w
N
w
∑
pdw=1
M
pdw
pos
M
pdw
neg
(12)
3.1 Overlapping Effects
Benchmark values are very similar with and without
block overlapping. Nevertheless, behaviors are not
the same. With block overlapping, the value associ-
ated to a cell depends on several blocks. Thus false
segment suppression (in particular on window bound-
aries) is less efficient (Figure 6). However, block
overlapping provides spatially finest study. In this
way, less silhouette segments are omitted by detec-
tion.
3.2 Cell and Block Size Effects
Cell size modifies SVM outputs spatial accuracy and
studied area relevance. Moreover bigger block size
leads to more efficient descriptors but spatially less
accurate results.
In Figure 7, the benchmark is computed with the L2-
norm. Blocks of 4 and 16 cells make block overlap-
CONTOUR SEGMENT ANALYSIS FOR HUMAN SILHOUETTE PRE-SEGMENTATION
77
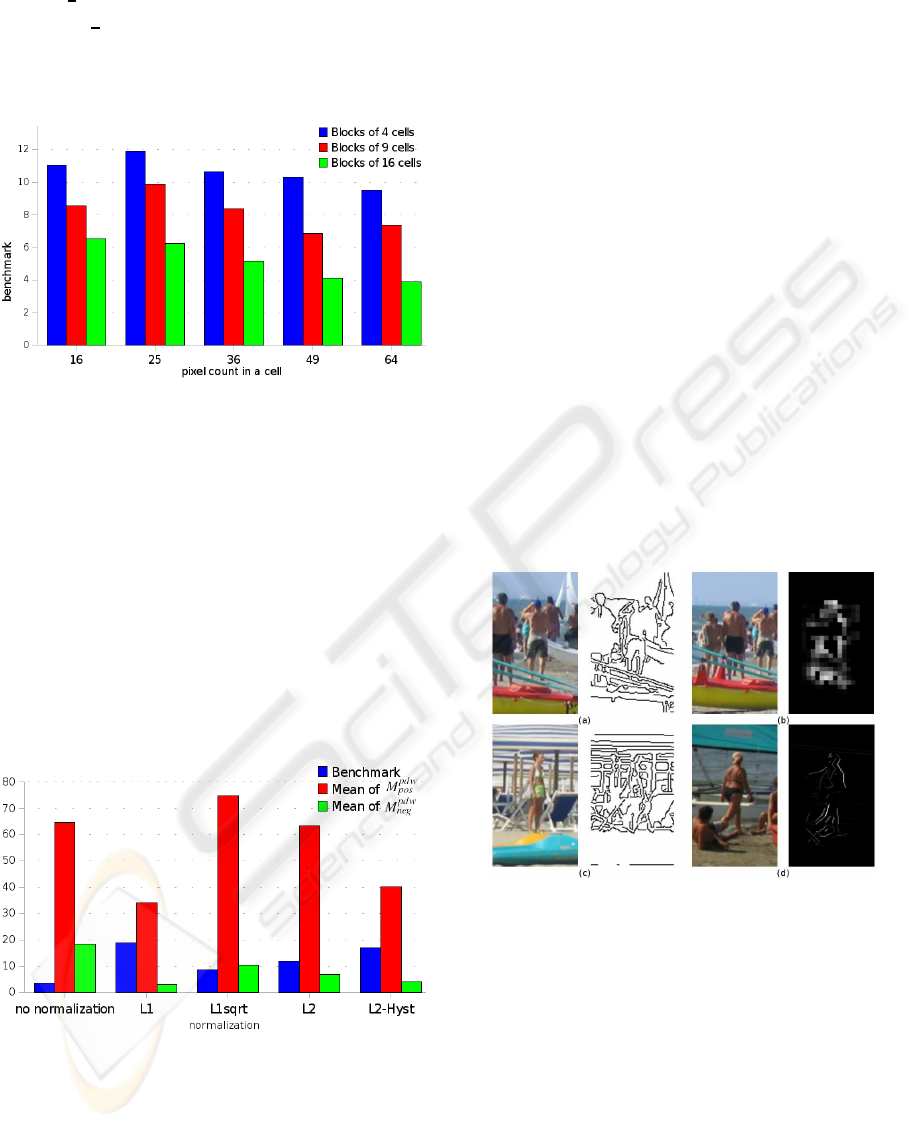
ping of
1
2
, while blocks of 9 cells make block over-
lapping of
1
3
. Blocks of 4 cells give the best results.
Results for various cell sizes are stable, but, for next
tests, cells of 25 pixels are used because they give the
best benchmark.
Figure 7: Cell and block size effects on the algorithm per-
formance.
3.3 Normalization Effects
Feature vector normalization prevents illumination
variation effects. The goal of this normalization is
to increase the similarity between images of the same
class. Results of Figure 8 stem from tests with blocks
of 4 cells of 25 pixels and block overlapping. Mean
of M
pdw
pos
, mean of M
pdw
neg
and benchmark are shown.
Without normalization, variations between elements
of the same class are higher. Thus, descriptor is less
discriminative and benchmark response is less good.
The benchmark promotes L1 and L2-Hyst norms.
Figure 8: Normalization effects on the algorithm perfor-
mance.
However, for these normalizations, mean of M
pdw
pos
is
low. That means that, with these norms, our method
is accurate but not efficient. L2-norm may also be the
best choice.
3.4 Particular Cases
Segmenting a person is harder if portions of the sil-
houette contours are missing (Figure 9a). Indeed, the
edge detector can miss parts of the silhouette if the
transition is not sharp enough. This has no influence
in computing, but perturbs segment gathering.
A typical detection and segmentation difficulty is
the occlusion (Figure 9b). If a part of the studied per-
son is hidden by an object, detection is a delicate is-
sue and segmentation suffers from contour disconti-
nuities. However, with our local study, each area is
independently studied. Thus, each segment can be lo-
cally likely, even though it is not linked to other likely
segments.
If the studied image has too cluttered background
(Figure 9c), edges are numerous. HOGs are so locally
perturbed and do not permit recognition.
Illumination can pose problems. In example (d)
of Figure 9, only a part of the leg is lighted. An edge
matches the leg and the background boundary while
another one matches the lighted and dark area bound-
ary. These two edges are close and parallel. Our
method can not recognize which one belongs to the
silhouette.
Figure 9: If a silhouette part does not belong to the com-
puted edges (right arm), segmentation is difficult (a). With
occlusion, the calfs are not detected but it does not perturb
the processing of feet (b). Cluttered background increases
difficulty (c). Illumination variations provide two parallel
edges in the leg (d).
4 CONCLUSIONS
This paper presented a method for quantifying the
likelihood of contour segment as being part of a hu-
man silhouette. To do that, in a positive detection
window, the HOGs that were previously computed for
people detection give a local description of his/her sil-
houette.
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
78

Figure 10: First column: INRIA’s database images. Second column: SVM outputs. Third column: likely segments obtained
by our method with block overlapping, L2-normalization and blocks of 4 cells of 25 pixels.
CONTOUR SEGMENT ANALYSIS FOR HUMAN SILHOUETTE PRE-SEGMENTATION
79

The main perspective of this work is to use this lo-
cal description to perform accurate segmentation. An
oriented graph may be created with all the contour
segments. The graph edges will be weighted with val-
ues found by our method. A shortest-path algorithm,
such as Dijkstra’s algorithm, will find the most likely
contour segment cycle representing the person’s sil-
houette.
REFERENCES
Alonso, I., Llorca, D., Sotelo, M., Bergasa, L., Toro, P. D.,
Nuevo, J., Ocania, M., and Garrido, M. (2007). Com-
bination of feature extraction methods for svm pedes-
trian detection. Transactions on Intelligent Trans-
portation Systems, 8:292–307.
Dalal, N. and Triggs, B. (2005). Histograms of oriented
gradients for human detection. Computer Vision and
Pattern Recognition, 1:886–893.
Freund, Y. and Schapire, R. (1995). A decision-theoretic
generalization of on-line learning and an application
to boosting. European Conference on Computational
Learning Theory, pages 23–37.
Joachims, T. (1999). Making Large-Scale SVM Learning
Practical. Advances in Kernel Methods - Support
Vector Learning, B. Schlkopf and C. Burges and A.
Smola, MIT-Press.
Kang, S., Byun, H., and Lee, S. (2002). Real-time pedes-
trian detection using support vector machines. Inter-
national Journal of Pattern Recognition and Artificial
Intelligence, 17:405–416.
Lin, Z., Davis, L., Doermann, D., and DeMenthon, D.
(2007). Hierarchical part-template matching for hu-
man detection and segmentation. International Con-
ference in Computer Vision, pages 1–8.
Munder, S. and Gavrila, D. (2006). An experimental study
on pedestrian classification. Transactions on Pattern
Analysis and Machine Intelligence, 28:1863–1868.
Munder, S., Schnorr, C., and Gavrila, D. (2008). Pedes-
trian detection and tracking using a mixture of view-
based shape-texture models. Transactions on Intelli-
gent Transportation Systems, 9:303–343.
Oren, M., Papageorgiou, C., Sinha, P., Osuna, E., and Pog-
gio, T. (1997). Pedestrian detection using wavelet
templates. Computer Vision and Pattern Recognition,
pages 193–199.
Ran, Y., Zheng, Q., Weiss, I., Davis, L., Abd-Almageed, W.,
and Zhao, L. (2005). Pedestrian classification from
moving platforms using cyclic motion pattern. In-
ternational Conference on Image Processing, 2:854–
857.
Sharma, V. and Davis, J. (2007). Integrating appearance
and motion cues for simultaneous detection and seg-
mentation of pedestrians. International Conference on
Computer Vision, pages 1–8.
Toth, D. and Aach, T. (2003). Detection and recognition
of moving objects using statistical motion detection
and fourier descriptors. International Conference on
Image Analysis and Processing, pages 430–435.
Tuzel, O., Porikli, F., and Meer, P. (2007). Human detection
via classification on riemannian manifolds. Computer
Vision and Pattern Recognition, 0:1–8.
Vapnik, V. (1995). The Nature of Statistical Learning The-
ory. Springer-Verlag, New York.
Wu, B. and Nevatia, R. (2007). Simultaneous object detec-
tion and segmentation by boosting local shape feature
based classifier. Computer Vision and Pattern Recog-
nition, 0:1–8.
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
80
