REAL-TIME INTERACTIVE L-SYSTEM

A Virtual Plant and Fractal Generator

Ludovic Hamon, Emmanuelle Richard, Paul Richard and Jean-Louis Ferrier

Laboratoire d’Ing

enierie des Syst

emes Automatis

es (LISA)

Universit

e D’Angers, 62, Avenue Notre Dame Du Lac, 49000 Angers, France

Keywords:

Virtual plant, L-systems, Real-time interaction, Haptic rendering, Augmented reality.

Abstract:

L-system is a rewriting process based on Chomsky grammar that can generate 3D fractals and virtual plants.

Its efﬁciency has been proved for more than twenty years with the works of Lindenmayer and Prusinkiewicz in

particular. This paper presents a Real-Time Interactive L-system (RTIL-system) allowing real-time rendering,

interactions with a user and/or the environment, haptic feedback and covering most of the important L-systems

extensions such as parametric and context sensitive features. Different potentialities of the RTIL-system are

illustrated where the user intervention becomes an essential element of plant/fractal evolution through Virtual

Reality and Augmented Reality applications.

1 INTRODUCTION

Plant modeling is used in various domains like botany,

agronomy, forestry, ecology, urban design, and even

video games. Virtual plants are computer simulations

of the growth, development and deployment of plants

in three-dimensional (3D) space. In Virtual Reality

(VR) or Augmented Reality (AR) applications, real-

time interaction with the virtual plants is required.

Moreover, in some applications involving tasks such

as pruning, physical properties may be added to en-

able haptic rendering and therefore the simulation re-

alism. In the last decades, several software applica-

tions have been developed. For example, Amap is

based on statistic measurements, Markov chains and

the Monte-Carlo method (Cirad, 2009). Another soft-

ware program called Xfrog was speciﬁcally devel-

oped for trees modeling (Lintermann and Deussenm,

1999). Vlab can generate, order and save an amount

of virtual plant models coming from different pro-

grams (Federl and Prusinkiewicz, 1999). GreenLab

adopted the AMAP discretization scheme and a dual-

scale automation (Reffye et al., 2003).

One of the most interesting software applications

is L-studio/cpfg/lpfg created in 1999 at the Univer-

sity of Calgary (Canada) by Prusinciewicz and co-

workers (Prusinkiewicz et al., 2000; Karwowski,

2002). It is based on L-system (Lindenmayer,

1968; Prusinkiewicz and Lindenmayer, 2004), a par-

allel rewriting process inspired by Chomsky gram-

mar. This formal mathematical approach can gener-

ate 3D virtual plants with realistic morphological and

physiological aspects.

Numerous applications are based on the L-system

model. However, to our knowledge, none of them are

simultaneously: (i) open source, (ii) with a good ren-

dering quality, (iii) in real time, (iv) covering most

of L-system essential extensions such as paramet-

ric and context sensitive features, and (v) interac-

tive. This paper presents a Real-Time Interactive L-

system (RTIL-system) allowing interaction between

virtual plants/fractals and both the user and the envi-

ronment. In addition, our approach takes into account

most important L-systems extensions. Collision de-

tection and haptic rendering of the virtual plant/fractal

are allowed. Different potentialities of the proposed

RTIL-system are illustrated through VR/AR applica-

tions such as interactive dynamic plants evolution,

pruning, constrained growing and an interactive frac-

tal. In the next section, the formalism and evolution

of L-systems focusing on real-time interactive appli-

cations are given. Section 3 is dedicated to the basic

features and the implementation of our RTIL-System.

Real-time interaction with the user and/or the envi-

ronment are described in section 4 with correspond-

ing applications. Finally a conclusion provides some

perspectives.

370

Hamon L., Richard E., Richard P. and Ferrier J. (2010).

REAL-TIME INTERACTIVE L-SYSTEM - A Virtual Plant and Fractal Generator.

In Proceedings of the International Conference on Computer Graphics Theory and Applications, pages 370-377

DOI: 10.5220/0002845703700377

 SciTePress

2 L-SYSTEMS: FORMALISM

AND EVOLUTION

2.1 Elementary Notions and Extensions

L-system is a formal language that was ﬁrstly used to

describe the development and proliferation of simple

multi-cellular organisms (Lindenmayer, 1968). Lin-

denmayer and Prusinkiewicz developed and extended

this language to model plants (Prusinkiewicz and

Lindenmayer, 2004). L-system is a triplet (V, w, P),

V being an alphabet, w being an axiom, and P being

a set of production rules. The couple (p,s) belonging

to the set production rules is composed of a prede-

cessor (p) and a successor (s). A derivation process

replaces the axiom symbols equal to predecessors by

the corresponding successors. If there is no corre-

sponding predecessor, then the symbol is replaced by

itself. After the axiom is completely reviewed, the

string obtained is called ”L-string”. Parametric L-

systems were important improvements in which each

symbol (called ”module”) may take a ﬁnite number

of real parameters (Prusinkiewicz and Lindenmayer,

2004). Furthermore, a logical condition was added to

each production rule that is applied if: (i) the current

symbol is equal to the rule predecessor, (ii) the num-

ber of parameters of symbol is equal to the number

of parameters of the rule predecessor, and (iii) if the

rule condition is true (Fig. 1). Thereafter, Linden-

w : B(2)A(4,4)

: A(x,y) : y ≤ 3 → A(x ∗ 2, x + y))

: A(x,y) : y > 3 → B(x)A(x/y,0)

: B(x) : x < 1 → C

: B(x) : x ≥ 1 → B(x − 1)

Figure 1: Example of parametric L-system evolution

(Prusinkiewicz and Lindenmayer, 2004).

mayer and Prusinkiewicz proposed the turtle geom-

etry concept (belonging to the LOGO Language) to

give a geometrical interpretation to the L-string. This

approach is based on an imaginary turtle that walks

and draws lines. In two dimensions, the turtle geome-

try concept is based on the triplet (x,y,a), (x,y) being

the position of the turtle, and a being the yaw angle

of the turtle movement. A simple example of con-

text free deterministic D0L-system is given in ﬁgure

2(a). The following interpretation symbols are intro-

duced with a stack that saves the turtle states as fol-

lows (Prusinkiewicz and Lindenmayer, 2004):

F : move a d distance forward and draw a line.

(x,y,a) ⇒ (x + d ∗ cos(a),y + d ∗ sin(a),a)

f : move a d distance forward without drawing a line

(x,y,a) ⇒ (x + d ∗ cos(a),y + d ∗ sin(a),a)

+ : turn left of o angle. (x,y,a) ⇒ (x,y,a + o)

− : turn right of o angle. (x,y,a) ⇒ (x,y,a − o)

[ : push the current turtle state to the stack.

] : pop the previous turtle state from the stack.

Lsystem : 1

derivation length : 4

Axiom : A

A →F[+A][−A]FA

F →FF

a b

Figure 2: Illustrations of D0L-systems: (a) a simple

model with corresponding axiom and production rules

(Prusinkiewicz and Lindenmayer, 2004); (b) a realistic rose-

bush (Favre et al., 2007).

In 1970s and 1980s several new forms of L-systems

appeared and numerous interpretation symbols were

proposed. For example, stochastic L-systems have

been developed to add a probability to each produc-

tion rule (Prusinkiewicz and Lindenmayer, 2004).

This feature allows the application of several rules to

the same symbol, which was not possible with de-

terministic L-systems. Pseudo L-systems have rule

predecessors that can be made up of several mod-

ules (Prusinkiewickz, 1986). Another interesting ex-

tension of L-systems is context sensitive L-system

REAL-TIME INTERACTIVE L-SYSTEM - A Virtual Plant and Fractal Generator

371

(called D1L-systems or D2L-systems). In a left (re-

spectively right) context sensitive L-system a rule is

applied only if the left (respectively right) symbol

of the current symbol is equal to the left (respec-

tively right) context of the current rule predecessor

(Prusinkiewicz and Lindenmayer, 2004).

Different applications with advanced graphical

rendering have appeared. For example, Baele and co-

workers have generated real time trees with different

detail levels, lightning and animation under wind us-

ing GPU capabilities (Baele and Warz

ee, ).

From 1990s to now, virtual plants generated by L-

system explicitly have described spatial distribution

of plant organs in three dimensions as a collection of

interconnected components. Furthermore, they model

the morphological and physiological aspects (Favre

et al., 2007) and the dynamic of plants population

(Bornhofen and Lattaud, 2007; Prusinkiewicz, 2009).

2.2 Interactions with the User

Many software applications dedicated to plant model-

ing exist and provide real-time basic interactions with

virtual plant such as rotation or zoom. These inter-

actions use the computer mouse and/or the keyboard

(Federl and Prusinkiewicz, 1999; Reffye et al., 2003;

Prusinkiewicz et al., 2000; Karwowski, 2002). How-

ever, some approaches have focused on advanced in-

teractions techniques. For example, Joanna et al. have

developed an interesting interactive L-system called

ILSA (Interactive L-String Arranger), based on the

Cpfg engine (Joanna et al., 1999; Prusinkiewicz et al.,

2000). The user can select plant components using a

mouse picking technique. The selection can be done

with two points on a branch (a starting and an ending

point). Operations like twisting, bending or pruning,

are possible. Interactive manipulations are executed

in semi real time, using a basic graphic rendering.

More recently, Onishi and co-workers have presented

a D0L-system in which 3D turtle cartesian coordi-

nates are directly sent to the environment (Onishi

et al., ). They use a magnetic tracking system to gen-

erate the trunk and the branches from hand move-

ments. Corresponding L-strings are generated and

branches are attached to the trunk by some speci-

ﬁed connecting points. The user is also able to spec-

ify some geometric primitives or draw silhouettes in

which parts of plant will grow up. Furthermore,

a component included in the selected zone may be

pruned, rotated, etc. These works provide some in-

teresting 3D interactions but are all based on simple

non-parametric D0L-systems limiting both the mod-

eling possibilities and animation rendering.

2.3 Interactions with the Environment

Another interesting feature of interactive L-systems

concerns interaction with the environment. The

Cpfg engine includes this possibility using a speciﬁc

module called ”Communication Module” (Mech,

1997). This module is presented by the follow-

ing syntax: ”?E(x1,. . . ,xn)”. It allows the program

to send and receive information from the environ-

ment. For example, suppose the following L-string:

”F(2)?E(1,2)F(3)F(5)F(5)”. Information sent to envi-

ronment is: position of the communication module in

the L-string and its parameters (here 1 and 2), turtle

state (position and orientation), name and parameters

of the module that follow the communication module

(here ”F(3)”). Information received from the environ-

ment is the parameters (x

,. . . ,x

) that can be mod-

iﬁed by this last one. A L-system with a commu-

nication module is called Open L-system. Open L-

system offers several interesting possibilities such as

handling collisions between plants organs or compo-

nents, pruning, water diffusion in soil, light distribu-

tion and several other interactions. However, a com-

munication module is required for each modules to

send the entire topological structure to the environ-

ment.

An interesting work on L-systems was done by Born-

hofen et al. who used a D0L-system to model dif-

ferent plants in a virtual garden. These plants grew

according to some environmental factors such as sun-

light and soil components (Bornhofen and Lattaud,

2007). In addition, the virtual plants are in competi-

tion for resources with respect of morphological and

physiological aspects.

3 RTIL-SYSTEM: BASIC

FEATURES

RTIL-system is based on Cpfg concepts and model

and uses a quite similar syntax. It is a library

written in C/C++ language that allows creating and

editing a script ﬁle and generating a 3D rendering

of the virtual plant using OpenGL library with op-

tional stereoscopic features for depth sensation en-

hancement (3DVision

T M

device from NVIDIA was

used). RTIL-system takes into account, determinis-

tic, context free, context sensitive, parametric, non

parametric and pseudo L-systems features . Homo-

morphism and decomposition rules are also available

(Prusinkiewicz et al., 2000; Karwowski, 2002).

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

372

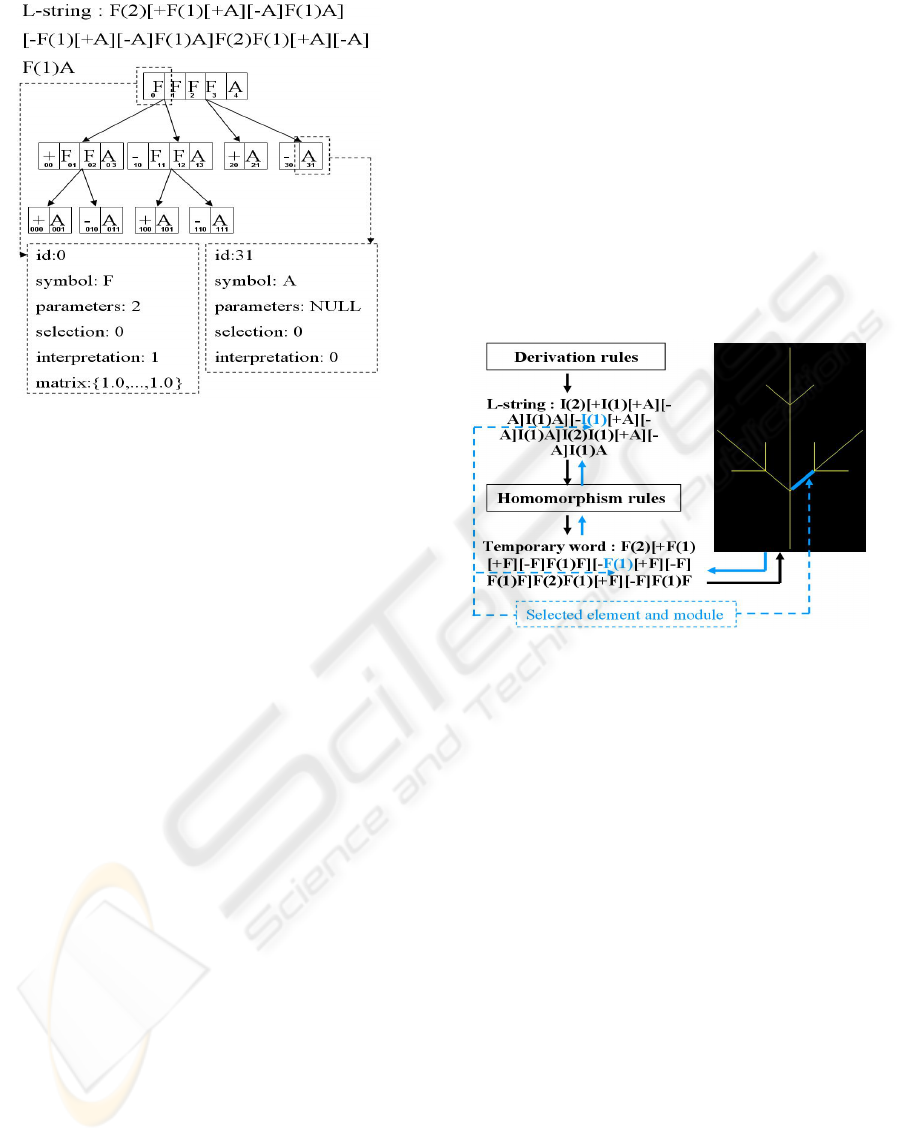
Figure 3: Tree structure of a L-string example.

3.1 Data Structure

A classic tree from computer science is used (ﬁg. 3).

Each node is composed of a ﬁnite set of modules. For

each module, the following attributes are recorded: (i)

an identiﬁer called id, (ii) its symbol, (iii) its param-

eters, (iv) a boolean variable (selection) that indicates

if the current module is selected by the user, (v) a

boolean variable (interpretation) that indicates if the

current module has a graphical representation. In the

case where ”interpretation” is true, some geometrical

information is added such as (vi) an OpenGL homo-

geneous matrix, etc..

3.2 Scripting and Syntax

A typical RTIL-system rule is presented as follows:

cg<pred>cd: C

cond C

→ succ, where ”pred” is

the predecessor, cg is the left context, cd is the right

context, cond is a logical proposition, C

and C

are C

langage instructions and ”succ” is the successor. Ac-

cording to the location of C language instructions in

the script, their respective executions are triggered as

follows: C

is executed if the predecessor and its con-

text correspond to the current L-string module and its

context. C

is executed if the previous condition for

execution is true and the logical proposition cond

is true. Other C language instructions can be included

after the Extern Start and Extern StartEach keywords.

The ﬁrst one indicates that the C instructions are exe-

cuted before the beginning of the ﬁrst derivation pro-

cess. The second one indicates that the C language

instructions are executed before each derivation pro-

cess. These instructions are limited to simple oper-

ators like, allocation, addition, substraction etc.. An

example (script1) with its graphical representation is

given below and illustrated in ﬁgure 4.

Lsystem : script1

Derivationlength : 2

Axiom : A

ExternStart : {c

= 0;s

= 0;}

ExternStartEach : {c

= 0;}

A → I(1)[+A][−A]I(1)A

I(x):{c

+1;} x≤10 {s

+1;}→ I(x ∗ 2)

Homomorphism

I(x) → F(x)

A → F

Figure 4: From L-string to graphical rendering : derivation

and homomorphism.

The derivation length is the number of required

derivation. The global variable ”c

” counts the num-

ber of call of second rule during the entire process.

The global variable ”s

” counts the application num-

ber of second rule. Homomorphism is an optional and

additional derivation process with speciﬁc rules that

follow homomorphism keyword. It is executed after

the L-string generation and creates a temporary word

(see black arrows in ﬁg. 4). Homomorphism process

is usually used to isolate the interpretation sequence

from the derivation sequence i.e: most of the inter-

pretation symbols are added with the homomorphic

derivation. It allows creating an accurate topological

formalism in which, for example, each plant compo-

nent possesses its own symbol, its own corresponding

rules as well as its own functions and operators.

REAL-TIME INTERACTIVE L-SYSTEM - A Virtual Plant and Fractal Generator

373

4 RTIL-SYSTEM INTERACTIVE

FEATURES

4.1 Data Transmission and Reception

The Extern Start and Extern EachStart keywords al-

low global variables deﬁnition. Global variables can

be seen and edited in real time by programs that in-

clude the RTIL library. A function func(id,x

,. . . ,x

)

can be included in the C language instructions and/or

in the module parameters. This function calls a func-

tion written in a C/C++ ﬁle, referred to ”id”, sends

,. . . ,x

) parameters and returns a real value. Thus,

advanced algorithms, functions, procedures and data

types belonging to C/C++ language may be used.

A speciﬁc procedure named com(x

,. . . ,x

) can be

called in C instructions. It sends (x

,. . . ,x

) param-

eters that could be modiﬁed by intern or extern pro-

grams. With this procedure, local variables and other

information are available to an environment that can

simulate light, collisions, soil distribution etc. Finally,

between two derivation steps, each graphical piece of

information linked to each interpretation module (i.e:

positions and orientations of the turtle geometry) can

be seen by programs including our RTIL-library.

Figure 5: Development of a virtual plant : unconstrained

evolution (a), and evolution constrained to the outside of a

sphere (b).

An example of interaction with the environment

is illustrated in ﬁgure 5. In this case the virtual plant

growth is constrained to the outside of a sphere. This

process is achieved thanks to rules similar as this one:

I(i) :{com(x);} (x == 1) → I(i + di). The procedure

com calls an ”environment” program that tests if the

position of the current graphical component linked to

the current internode I is inside the sphere or not. If

not, then x is set to 1 and the current internode I is

lengthened by di. In the opposite case, the internode

stops growing.

Figure 6: A child feeding a virtual plant using an AR inter-

action technique.

An interesting application based on our RTIL-

system is illustrated in ﬁgure 6. The aim of this AR

application was to make children (i) learn about some

fundamental needs of plants (water, heat and light)

and (ii) become aware of differences in plant needs

throughout their life cycle. Using a menu-based in-

teraction technique, the child can bring various quan-

tities of these three fundamental needs to a virtual

plant, and observe their effect on the germination,

growth and reproduction steps. The three needs are

deﬁned using global variables that are updated be-

tween two derivation steps. Depending on their val-

ues, positive or negative rules are applied to the plant

evolution. A possible evolution of the virtual plant

is illustrated in ﬁgure 7. An experiment in which

twenty-four K4-K5 children were instructed to make

a virtual plant grow was carried out and the results are

exposed in a paper called ”Real-Time Interactive L-

system for Virtual Plants, An Augmented Reality Ed-

ucational Application”, submitted for a Special Issue

on Augmented Reality on November 2009. (Virtual

Reality Journal, 2010).

Figure 7: Illustration of a possible evolution of the virtual

plant : ﬂowering stage (a), followed by a lack of water and

excess of heat (b)(c)(d), and then by a correct feeding (e)(f).

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

374

4.2 Graphical Interaction and Haptic

Rendering

Graphical interaction with the virtual plant requires

the three following steps: (i) select one (or more) 3D

component(s), (ii) ﬁnd the corresponding module(s)

in the L-string (see blue arrows in ﬁg. 4), and (iii) ap-

ply a corresponding action on the selected module(s).

For example, a pruning task consists in the removal

of a graphic element coupled with the deletion of the

corresponding module in the L-string. Some difﬁcul-

ties may appear when linking the graphical compo-

nent to the corresponding L-string module whereas

homomorphism concept and pseudo L-systems al-

low the creation of different L-system scripts gen-

erating the same graphical shape and behavior. Let

us consider the script1 with the ﬁrst homomorphic

rule I(x) → F(x) replaced by this one: I(x) →

F(x/2)F(x/2). This change leads to the same graph-

ical rendering but the application is not bijective.

Thus, apart from L-systems without homomor-

phism process, graphical selection tasks necessarily

require that the predecessor of each homomorphic

rule has the same number of modules as the corre-

sponding successor (proposition 1). Consequently, to

preserve the current formalism and to avoid this prob-

lem, RTIL-system homomorphic rules are limited to

proposition 1.

4.2.1 3D Interaction Devices

For the selection of a graphic component of the plant,

our RTIL-system allows the integration of different

types of 3D interaction devices such as the (i) the

Polhemus Patriot

T M

electromagnetic tracking device

from Polhemus or (ii) the PhantomOmni

T M

desk-top

haptic interface from Sensable (ﬁg. 10). Selection of

plant components is achieved using a collision detec-

tion algorithm involving a spherical cursor (ﬁg. 11)

and the geometrical model associated with the se-

lected component.

4.2.2 Selection: Collision Detection and Haptic

Rendering

In order to handle collision detection and provide hap-

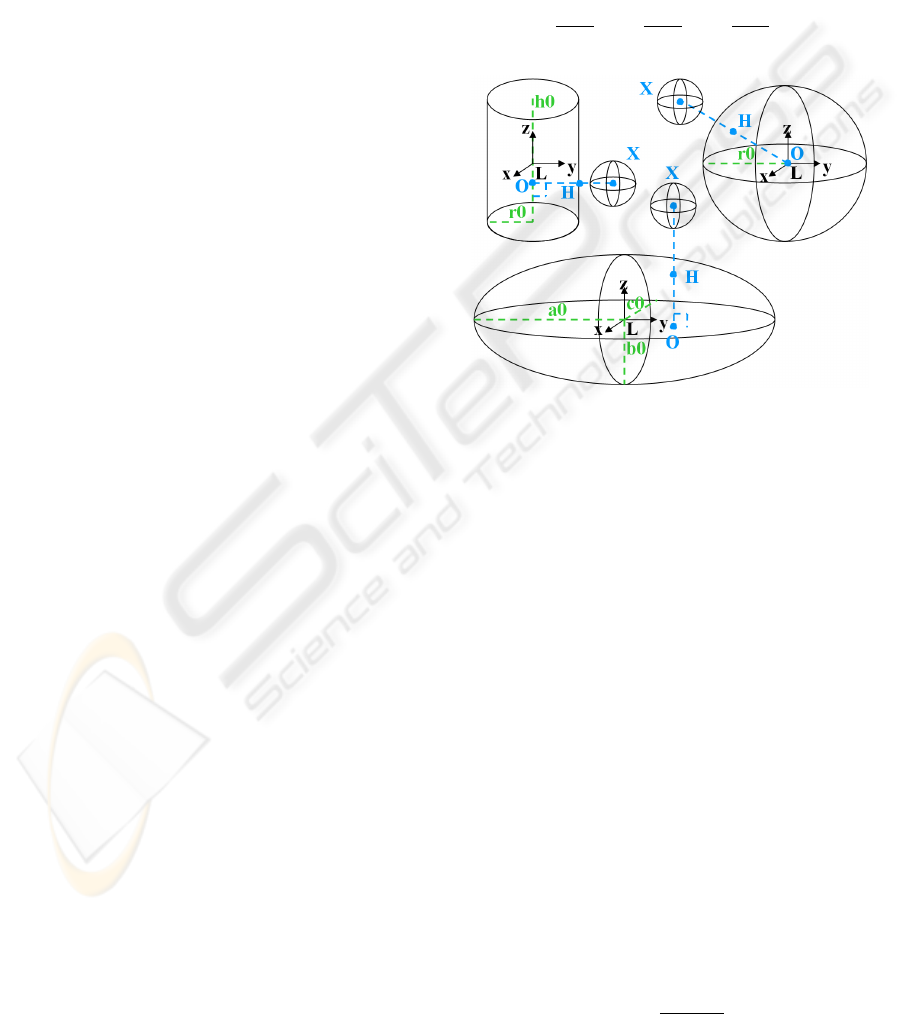
tic rendering, RTIL system associates a geometrical

primitive to each plant component (Fig. 8): (i) a

cylinder for roots, branches, trunks, internodes and

fractal components (ii) a sphere for seeds and fruits,

(iii) and an ellipsoid for leaﬂets, leaves and sepals

(merged with the (LX,LY) surface plan). Figure 9

shows both graphical and physical models of a virtual

ﬂower, and their superimposition.

Thus, the selection of a component of the plant re-

quires that the center X(x

) of the spherical cur-

sor with radius r is solution to one of the follow-

ing equations according to the geometrical primitive,

where L(x

) is the origin of the local cartesian

space (ﬁg. 8) :

Cylinder : (0 ≤ y

≤ h

) and

((x

− x

)

+ (z

− z

)

≤ (r + r0)

)

Sphere :

− x

)

+ (y

− y

)

+ (z

− z

)

≤ (r + r0)

Ellipsoid : (

−x

)

+ (

−y

)

+ (

−z

)

≤ 1

Figure 8: Three geometrical models used for collision de-

tection and haptic rendering : (a) a cylinder for roots,

branches, trunks, internodes and fractal components ; (b)

a sphere for seeds and fruits ; and (c) an ellipsoidal surface

for leaﬂets, leaves and sepals.

A blue color shows that a component is selected.

Force feedback vectors have been implemented when

the PhantomOmni

T M

haptic interface is used thanks

to RTIL library. For each physical element, two points

have been calculated depending on ”X” point loca-

tion: ”O” is the center of the physical sphere (or

respectively, the orthogonal projection of X on the

cylinder axe, or the orthogonal projection of X on the

(LX,LY) ellipsoid plan), and ”H” is the intersection

of OX line and the physical sphere surface (or respec-

tively the cylinder surface, or the ellipsoid surface)

(ﬁg. 8).

With these two points, two simple forces

−→

F have

been created in the cartesian space: an attractive force

that attracts the Phantom Omni inside the physical

representation if k

−→

OXk ≥ (k

−→

OHk+ r), and a repulsive

force that allows the Phantom Omni sliding along the

physical representation if k

−→

OXk > ε:

−−−−→

NorPos =

−→

OX, Normalize(

−−−−→

NorPos),

Attractive Force:

−→

F = −

sti f f ness1

−→

OXk

−−−−→

NorPos

REAL-TIME INTERACTIVE L-SYSTEM - A Virtual Plant and Fractal Generator

375

Figure 9: A virtual ﬂower : (a) graphical model ; (b) phys-

ical model ; and (c) superimposition of both graphical and

physical models.

Repulsive Force:

−→

F =

sti f f ness2

−→

OXk

−−−−→

NorPos

Figure 10: A user working on a virtual plant, with Phantom

Omni device, force feedback and stereoscopic viewing.

The ﬁrst effect constrains the user to navigate in-

side and along the virtual object. The stiffness coefﬁ-

cient adjusts the attraction force. With the second ef-

fect touch sensation appears. The virtual object seems

rigid with a high value of stiffness coefﬁcient or soft

with a low value. Figure 10 shows a user perform-

ing tasks with force feedback in stereoscopic viewing

condition.

4.2.3 Deletion and Pruning

When one or more graphical components are selected

by the user, with the help of dedicated interfaces, they

can be pruned. That leads to: (i) the deletion of the

corresponding modules in the data-structure (ﬁg. 3),

(ii) the deletion of all modules that follow these last

ones in the same node, (iii) and the recursive deletion

of all ”son” nodes that are linked to previous erased

”father” modules in (i) and (ii) (ﬁg. 11, (b) and (c)).

4.2.4 Partial Interactive Derivation

Our RTIL-system introduces a new keyword called

Interaction in the script ﬁle (ﬁg. 12). It is followed

by a ﬁnite set of rules called ”Interaction Rules” that

can be applied to selected modules only. With this

feature, the concept of Partial Interactive Derivation

Figure 11: Illustration of a simple pruning task : the virtual

Phantom Omni stylus (a), selection of an internode of the

virtual plant (b), and deletion (c).

is introduced i.e: one or more derivation steps with

Interaction Rules on only selected modules. If there

are no Interaction rules, usual rules replace them. A

large set of possible interactive tasks such as bend-

ing/twisting components, partial development, elon-

gation/reduction of components, breaking, insertion

of elements etc. . . are available with Partial Interac-

tive Derivation.

Lsystem : script2

Axiom : A + + + A + + + A

A →A − A + +A − A

Interaction

A →A − A + +A − A

Homomor phism

A →F

Figure 12: A half divided Koch fractal snowﬂake.

For example, Figure 12 shows a mutated ”Koch

Fractal snowﬂake”. From a normal Koch snowﬂake

in (a), user selects two components in (b) and (c).

With application of the Koch interactive rule ”A →

A − A + +A − A” to selected components, a half di-

vided snowﬂake is obtained in (d). Then (e) and (f)

are the results of two classic derivations on the entire

object.

Another example illustrating the Partial Interac-

tive Derivation process is shown in ﬁgure 13. A bug,

represented by a red sphere, is placed (b) on a selected

component of the virtual plant (a) thanks to the fol-

lowing interaction rule: I(i) → BI(i) (I: inter-node, B:

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

376

bug). As a consequence of several normal derivations,

the bug climbs along the current axis of the plant and

eats the ﬂower (c). This induces an apical dominance

phenomenon leading to the outgrowth of a lateral bud

(c).

With respect of the L-system concept, ”Partial In-

teractive Derivation” lead to open L-system formal-

ism to advanced interactions where user can create,

edit, control part or entire derivation process and be-

comes an important element of the model evolution.

Figure 13: Example of a Partial Interactive Derivation pro-

cess: a bug is placed (b) on the selected component (a),

climbs along the axis and eats the ﬂower, and the result is

the outgrowth of a lateral bud (c).

5 CONCLUSIONS

This paper presents a Real-Time Interactive L-system

(RTIL-system) allowing interactions with both the

user and the environment. RTIL-system takes into ac-

count most important L-systems extensions such as

parametric and context sensitive features. In order to

preserve L-systems formalism and allow advanced in-

teractions, the Partial Interactive Derivation concept

is introduced. It allows the deﬁnition of Interaction

Rules that can be applied on selected modules only.

Collision detection and haptic rendering of the vir-

tual plants are also provided. Different potentialities

of the RTIL-system are illustrated through VR/AR

applications such as interactive dynamic plants evo-

lution, pruning, constrained growing and a mutated

Koch fractal. In future work we plan to run experi-

ments that will aim to investigate human performance

in tasks involving multimodal interaction with virtual

plants. Real time advanced graphical rendering tech-

nics will be explored. In addition, we will used our

RTIL-system to generate different geometrical forms

and interact with force feedback.

REFERENCES

Baele, X. and Warz

ee, N. Real time l-system generated

trees based on modern graphics hardware. In Inter-

national Conference on Shape Modeling and Applica-

tions, SMI’05 2005.

Bornhofen, S. and Lattaud, C. (2007). Evolution of virtual

plants interacting with their environment. In Proceed-

ings of the 9th International Conference on Virtual Re-

ality (VRIC’07).

Cirad (2009). Amap website, http://amap.cirad.fr.

Favre, P., Gu

eritaine, G., Andrieu, R., and Boumaza, R.

(2007). Modelling the architectural growth and de-

velopment of rosebush using l-systems. In Workshop

on Growth Phenotyping and Imaging in Plants.

Federl, P. and Prusinkiewicz, P. (1999). Virtual labora-

tory: An interactive software environment for com-

puter graphics. In Proceedings of Computer Graphics

International.

Joanna, L., Power, A., Bernheim, B., and Prusinkiewicz, P.

(1999). Interactive arrangement of botanical l-system

models. In Proceedings of the Symposium on Interac-

tive 3D Graphics, pages 175–182.

Karwowski, R. (2002). Improving the process of plant mod-

eling: The l+c modeling language. Ph.D. dissertation,

University of Calgary, Canada.

Lindenmayer, A. (1968). Mathematical models for cellular

interactions in development. in Journal of Theoretical

Biology parts I and II, pages 280–315.

Lintermann, B. and Deussenm, O. (1999). Interactive mod-

elling of plants. In IEEE Computer and Application,

volume 19, pages 2–11.

Mech, R. (November 1997). Environment using l-systems

and their extensions. PhD thesis, University of Cal-

gary, Canada.

Onishi, K., Murakami, N., Kitamura, Y., and Kishino, F.

Modeling of trees with interactive l-system and 3d

gestures. In International Workshop on Biologically

Inspired Approaches to Advanced Information tech-

nology, pages 222–235.

Prusinkiewickz, P. (1986). Graphical applications of l-

systems. In Proceedings of Graphical Interface and

Vision Interface 86, pages 247–253.

Prusinkiewicz, P. (2009). publications 1986 - 2009,

http://algorithmicbotany.org/papers/.

Prusinkiewicz, P., Karwowski, R., Mech, R., and Hanan, J.

(2000). L-studio/cpfg: A software system for model-

ing plants. Nin Nagl M., Schrr A. and Mnch M. (eds.),

Applications of Graph Transformations with Indus-

trial Relevance,Lecture Notes in Computer Science.

Prusinkiewicz, P. and Lindenmayer, A. (1990–2004). The

algorithmic beauty of plants. Springer Verlag.

Reffye, P., Zhao, X., Yan, H., and Kang, M. (2003). Green-

lab: a new methodology towards plant functional-

structural model - structural aspec. In Proceedings

PMA03 : 2003’ International symposium on plant

growth modeling, simulation, visualization and their

applications.

REAL-TIME INTERACTIVE L-SYSTEM - A Virtual Plant and Fractal Generator

377