EXTENDING REVISED AFFINE ARITHMETIC FOR FAST
RELIABLE RAY-TRACING OF PROCEDURALLY DEFINED
IMPLICIT SURFACES
Oleg Fryazinov, Alexander Pasko and Peter Comninos
The National Centre for Computer Animation, Bournemouth University, U.K.
Keywords:
Ray tracing, Implicit surfaces, Function representation, Revised Affine Arithmetic.
Abstract:
Fast and reliable rendering of implicit surfaces is an important research area in the field of implicit mod-
elling. Direct rendering, namely ray-tracing, is shown to be a suitable technique for obtaining good-quality
visualisations of implicit surfaces. We present a technique for reliable ray-tracing of arbitrary procedurally
defined implicit surfaces by using a modification of Affine Arithmetic called Revised Affine Arithmetic. A
wide range of procedurally defined implicit objects can be rendered using this technique including polynomial
surfaces, constructive solids, pseudo-random objects, procedurally defined microstructures, and others. We
compare our technique with other reliable techniques based on Interval and Affine Arithmetic to show that
our technique provides the fastest, while still reliable, ray-surface intersections and ray-tracing. We also sug-
gest possible modifications for the GPU implementation of this technique for real-time rendering of relatively
simple implicit models and for near real-time rendering of complex implicit models.
1 INTRODUCTION
In recent years, implicit surfaces (isosurfaces of
trivariate real functions) have proved to be a power-
ful and simple solution to some complex problems in
the area of modelling and animation. For example,
implicit surfaces provide solutions for surface recon-
struction from scattered points and for fluid simula-
tion. Several operations, such as sweeping, metamor-
phosis and offsetting can be implemented quite eas-
ily with implicit models unlike traditional boundary-
representation models. However, modelling with the
whole range of implicit surfaces is still a complicated
task because interactiverenderingof arbitrary implicit
surfaces is still an open problem. Currently, there
are two ways to render an implicit model: generation
of a polygonal mesh and direct rendering using ray-
tracing. Polygonization is a widely used technique,
but in many cases, when the model has sharp or thin
features, large numbers of small-sized disjoint ele-
ments or internal microstructures, the generation of an
appropriate polygonal mesh takes a long time and re-
quires a large amount of memory. A more promising
technique is that of interactive direct rendering of im-
plicit surfaces using ray-casting and ray-tracing. Tra-
ditionally the main disadvantage of direct rendering
was their slow speed due to the large number of ray-
surface intersection calculations. With recent devel-
opments of hardware this problem becomes less criti-
cal, but not insignificant all together.
Many techniques of ray-tracing implicit surfaces
have been developed. However, the majority of these
techniques have disadvantages, because they either
work with a small range of implicit surfaces (for in-
stance those defined only by polynomials), or not reli-
able. For example, classical approximate techniques,
such as ray marching, are fast, but can easily miss
sharp features and small components of these models.
Classical numerical techniques, such as the Newton
search require different signs of the defining function
at the ends of the ray interval, which is inappropriate
for arbitrary rays. Sphere-tracing based techniques
require a distance property of the defining function,
which can not be provided for general models. Tech-
niques based on interval analysis and other reliable
numerical computations have also been applied to the
ray-tracing of implicit surfaces. However, classical
Interval Arithmetic is slow because of the interval
199
Fryazinov O., Pasko A. and Comninos P. (2010).
EXTENDING REVISED AFFINE ARITHMETIC FOR FAST RELIABLE RAY-TRACING OF PROCEDURALLY DEFINED IMPLICIT SURFACES.
In Proceedings of the International Conference on Computer Graphics Theory and Applications, pages 199-207
DOI: 10.5220/0002847501990207
Copyright
c
 SciTePress

overestimation.
The problem considered in this paper is that of
finding a technique for ray-tracing general implicit
surfaces, that has the following properties: a) Its ray-
surface intersection procedure should be reliable, i.e.
no roots should be missed; b) A wide range of im-
plicit models should be supported – meaning that the
algorithm should be able to work with procedurally
defined models as well as with algebraic ones; c) The
procedure should be fast and suitable for a GPU im-
plementation for interactive rendering.
In this paper we propose to use Revised Affine
Arithmetic (RevAA in the text) as a fast and reli-
able technique for calculating the range of a function
for a given interval and hence for the core for the
ray-surface intersection procedure. Also we extend
affine arithmetic by affine forms related to the pro-
cedural definition of the model to decrease the num-
ber of computations while evaluating the interval for
the function and hence decrease the rendering time.
The main contributions in this paper are: 1) widen-
ing the scope of the reliable ray-tracing from alge-
braic surfaces defined by polynomials to general im-
plicit surfaces defined by function evaluation proce-
dures involving both affine and non-affine operations
based on Revised Affine Arithmetic; 2) a technique
to represent the procedural model by using special
affine forms with a case study of affine forms for set-
theoretic operations in form of R-functions; 3) a tech-
nique for optimising the proposed ray-tracing proce-
dure by using argument pruning applied to Revised
Affine Arithmetic.
2 RELATED WORK
Ray-tracing of implicit surfaces is a well-researched
area. Most of the techniques described in a survey
(Hart, 1993) are approximate and can miss small sur-
face features, but on the other hand, they are suitable
for all types of implicit surfaces. Later, several tech-
niques were presented for particular types of implicit
surfaces that provided not only an increase in speed
but also reliability. Thus, in (Hart, 1994) a distance
property is needed for the ray-tracing procedure, in
(Sherstyuk, 1999) blobs, metaballs and convolution
surfaces are the types of implicit surface that can be
rendered fast.
Other ways to increase speed of ray-tracing are
by reducing the number of processed rays intersect-
ing the implicit surface and by using specialized
hardware, for example graphical processors (GPUs).
In (Hasan, 2003), the number of processed rays
is reduced by using image-space subdivision, while
(Gamito and Maddock, 2007a) uses progressive re-
finement. GPU-based ray-tracing of implicit surfaces
was introduced only for particular types of the ob-
jects, such as radial-basis functions (Corrigan and
Dinh, 2005). Ray-tracing of general implicit surfaces
on the GPU was performed in (Fryazinov and Pasko,
2008) and in (Singh and Narayanan, 2009) by using
approximate methods.
Reliable computational techniques based of In-
terval Arithmetic have been known for a long time.
However, most of the literature relates to fields such
as global optimisation rather than computer graphics.
The works of (Mitchell, 1991) and (Snyder, 1992) dis-
cussed applications of Interval Arithmetic for com-
puter graphics purposes, and Affine Arithmetic was
used for ray-tracing of implicit surfaces in (de Cusatis
Jr. et al., 1999) . A good comparison of different
interval techniques can be found in (Martin et al.,
2001), however the list of the implicit models used
in this paper is limited to those given in the polyno-
mial form. In (Gamito and Maddock, 2007b) the Re-
duced Affine Arithmetic was introduced for the pur-
poses of stochastic implicit model rendering. How-
ever, the Reduced Affine Arithmetic could not be used
for general implicit models, as only affine operations
and multiplication were supported. Interval Arith-
metic and Reduced Affine Arithmetic are applied for
fast rendering of implicit surfaces by using the GPU
in (Knoll et al., 2009). A more detailed comparison
of these techniques with the one proposed here can be
found in the ”Results” section below. In this paper,
we use Revised Affine Arithmetic (Vu et al., 2009),
which was introduced recently for the purposes of
constraint propagation and has not yet been used in
computer graphics.
3 BACKGROUND
3.1 Procedurally Defined Implicit
Surfaces
A zero level set or an isosurface of a trivariate real
function f of a point with coordinates (x,y,z) is tra-
ditionally called an implicit surface and is defined as
f(x,y,z) = 0. It can also be considered as the bound-
ary of a solid (three-dimensional manifold) defined by
the inequality f(x,y, z) ≥ 0. There are many different
ways to specify the function f(x,y,z). The simplest
form is that of an algebraic implicit surface defined
by a polynomial function. Most of the extant work on
reliable ray-tracing concentrates solely on algebraic
surfaces. More complex forms involve exponential,
GRAPP 2010 - International Conference on Computer Graphics Theory and Applications
200

square root, trigonometric and other non-linear func-
tions. We deal with the most general form of proce-
durally defined implicit surfaces, where the function
f is evaluated by some procedure involving all kinds
of non-linear functions as well as loops and condi-
tional operations. This allows us to cover skeleton-
based implicit surfaces, Constructive Solid Geometry
(CSG) objects defined by nested R-functions, solid
noise, fractals and other complex objects.
3.2 Affine Arithmetic
Affine Arithmetic (AA) is a technique for perform-
ing computations on uncertain numerical values. The
main idea of AA is the calculation of an uncertain
value (function) based on other uncertain values (ar-
guments). Initially this model was introduced for self-
validated numerical computations as an alternative to
Interval Analysis and currently it is used in many dif-
ferent areas of computer science (de Figueiredo and
Stolfi, 1997). By keeping track of the errors for each
computed quantity, AA provides much tighter bounds
for computed quantities compared to classical Interval
Arithmetic. Uncertain values in AA are represented
by affine forms, i.e. polynomials of the form
ˆx = x
0
+ x
1
ε
1
+ x
2
ε
2
+ ... + x
n
ε
n
where x
n
are known real coefficients and ε
n
are noise
symbols, i.e. symbolic variables whose values are as-
sumed to lie in the interval ε
n
∈ [−1, 1].
All operations on affine forms can be divided
into affine (exact) and non-affine (approximate) op-
erations. An affine operation is a function that can
be represented by the linear combination of the noise
symbols of its arguments. For example, a multiplica-
tion by a constant is an affine operation:
αˆx = αx
0
+ αx
1
ε
1
+ αx
2
ε
2
+ ... + αx
n
ε
n
Non-affine operations can not be performed over the
linear combination of the noise symbols. In this case
an approximate affine function is used and a new
noise symbol is added to the affine form to represent
the difference between the non-affine function and its
approximation.
In the general case any non-affine operation can
be represented in an affine form:
ˆx⊗ ˆy = αˆx+ βˆy+ ζ ± δ
where the value of the new noise symbol is repre-
sented by δ. In (de Figueiredo and Stolfi, 1997),
different approximation techniques are discussed for
the affine form of several functions: Optimal (Cheby-
shev), Min-range and Interval approximation. While
optimal and min-range approximation require the
function to be bounded, twice differentiable and with
the same sign of the second derivative on the given
argument range, the interval approximation requires
only the function to be bounded, however the range of
the function for interval approximation is wider than
for other approximations.
3.3 Revised Affine Arithmetic
Pure AA is both computationally and memory expen-
sive and can not be used in algorithms where the re-
duction of computational complexity is equally im-
portant as the quality of the computational result. In
(Messine, 2002), several reduced affine forms were
introduced to reduce the number of computations in
Affine Arithmetic by accumulating errors. The Affine
Form 1 (AF1) is the simplest one and represents the
uncertain quantity as:
ˆx = x
0
+
n
∑
i=1
x
i
ε
i
+ x
n+1
ε
n+1
The noise symbols ε
1
,...,ε
n
represent the errors of the
initial arguments. The last noise symbol represents all
the errors after the non-affine operations.
Revised Affine Arithmetic is an extension of AF1
and was introduced by Vu et al. (Vu et al., 2009)
for the purposes of numerical constraint propagation.
The revised affine form is similar to AF1:
ˆx = x
0
+
n
∑
i=1
x
i
ε
i
+ e
x
[−1,1],e
x
≥ 0
The general binary affine operation is defined as:
f( ˆx, ˆy) = (αx
0
+ βy
0
+ ζ) +
n
∑
i=1
(αx
i
+ βy
i
) + (δ+
|α|e
x
+ |β|e
y
)[−1,1]
where α, β and ζ can be taken from the affine ap-
proximation of the function f. The affine operation
with one operand and more than two operands can be
defined in the same way.
RevAA uses a special tight form for the multipli-
cation operation:
ˆx ∗ ˆy = (x
0
y
0
+
1
2
n
∑
i=1
x
i
y
i
) +
n
∑
i=1
(x
0
y
i
+ x
i
y
0
)ε
i
+
e
xy
[−1,1], where e
xy
= e
x
e
y
+ e
y
(|x
0
| + u) + e
x
(|y
0
| +
v) + uv−
1
2
n
∑
i=1
|x
i
y
i
|, u =
n
∑
i=1
|x
i
|, v =
n
∑
i=1
|y
i
|.
As for standard AA, RevAA has an inclusion
property. In our technique we use the shortest pos-
sible revised affine form, i.e. n = 1 as it is most con-
venient for the purposes of ray-tracing and requires
fewer computations than with a greater n.
EXTENDING REVISED AFFINE ARITHMETIC FOR FAST RELIABLE RAY-TRACING OF PROCEDURALLY
DEFINED IMPLICIT SURFACES
201

4 RAY-TRACING WITH REVISED
AFFINE ARITHMETIC
The main part of any ray-tracing procedure for im-
plicit surfaces is the calculation of the zero roots of
the defining function in the ray-surface intersection
procedure. In this section we show how RevAA can
be used for the intersection point calculation and we
present several techniques for speeding up this calcu-
lation.
4.1 Ray-Surface Intersection
Our algorithm is based on a ray-surface intersection
technique for implicit surfaces that uses interval tech-
niques, which originally appeared in (Mitchell, 1991).
We present the ray-surface intersection procedure in
Algorithm 1.
Algorithm 1: Ray-surface intersection.
Procedure: bool intersect(t
min
, t
max
)
Calculate the affine form F for the function on the
interval [t
min
,t
max
]
Get the range of the function from the affine form
if the range of the function does not include a 0
value then
return FALSE (no roots in this interval);
end if
Calculate the argument estimation from the affine
form: t
′
min
,t
′
max
Find the pruned argument range:
t
min
= max(t
min
,t
′
min
);
t
max
= min(t
max
,t
′
max
);
if the length of the argument interval is less than
some predefined accuracy then
Store the midpoint of the interval as the root;
return TRUE;
end if
Calculate the midpoint of the argument range:
t
mid
= (t
min
+ t
max
)/2;
Repeat the procedure for the two subintervals:
bool b1 = intersect(t
min
,t
mid
);
if b1 is TRUE and only the first root is needed then
return TRUE;
end if
bool b2 = intersect(t
mid
,t
max
);
if b2 is TRUE then
return TRUE;
end if
return FALSE;
The basic idea of the algorithm is quite simple:
we calculate the range of the function for the given
Figure 1: The revised affine form for the function on
the two subintervals after the dichotomy on the interval
[t
min
,t
max
].
argument interval using RevAA, we reject the inter-
val if the range does not include the zero value, oth-
erwise we subdivide the interval into two intervals by
using dichotomy and we repeat the procedure for both
subintervals. An example of the affine form for the
function after the dichotomy is shown in the figure 1.
Note that in the case when only the first root is needed
(for example, for primary rays), we can exit from the
procedure earlier if we have found a root in the first
subinterval after the recursive procedure.
4.1.1 Affine Form Calculation and Interval
Range for the Function in RevAA
The basic revised affine form for the function is ob-
tained from the procedural definition of the function
by replacing all the operations on real numbers by op-
erations on the revised affineforms of coordinate vari-
ables: ˆx = x
0
+
ˆ
t ∗ d
x
, ˆy = y
0
+
ˆ
t ∗ d
y
, ˆz = z
0
+
ˆ
t ∗ d
z
,
where x
0
,y
0
,z
0
are the coordinates for the ray ori-
gin and d
x
,d
y
,d
z
are the components for the ray di-
rection vector and are constant for each ray, and
ˆ
t =
t
min
+t
max
2
+
t
max
−t
min
2
ε
1
is an affine form for the argu-
ment interval.
Non-arithmetic operations, such as trigonometric,
logarithmic and reciprocal, can be calculated by us-
ing the general affine form applied to RevAA. The
formulation for the coefficients of the general affine
form and most of the basic non-arithmetic operations
can be found in (de Figueiredo and Stolfi, 1997).
We propose also to extend the number of opera-
tions by calculating affine forms for functions used in
the procedural definition of the implicit model. As a
case study we present the formulation for set-theoretic
(CSG) operations using R-functions as follows:
R
uni
( f
1
, f
2
) = f
1
+ f
2
+
q
f
2
1
+ f
2
2
GRAPP 2010 - International Conference on Computer Graphics Theory and Applications
202

R
int
( f
1
, f
2
) = f
1
+ f
2
−
q
f
2
1
+ f
2
2
where R
uni
is the function for set-theoretic union
and R
int
is the function for set-theoretic intersection
(Shapiro, 2007). The optimal and min-range ap-
proximations can be obtained for these functions, be-
cause the requirements are satisfied, however the op-
timal approximation is computationally expensive for
these particular functions comparing to the natural
extension of these functions in RevAA. We propose
to use the min-range approximation for these func-
tions. By analogy with the construction of an approx-
imation for the function of one variable presented in
affine arithmetic-related literature, our approximation
is constructed by using these rules:
• α =
∂R
∂x
, β =
∂R
∂y
, where partial derivatives are
taken at the base point, i.e. minimal point (x =
x
min
,y = y
min
) for the union operation and maxi-
mal point (x = x
max
,y = y
max
) for the intersection
operation because of the second derivative sign.
Note that the base point should not be [0, 0] be-
cause of the discontinuity of the first derivative
and an opposite point should be selected instead.
• We calculate the distance to the other cor-
ner points of the surface patch z = R(x, y),x ∈
[x
min
,x
max
],y ∈ [y
min
,y
max
] by using the equation
of the plane R(x,y) = αx+ βy+ d. Note that for
the base point d = 0, a maximal distance d
max
be-
tween the three points is taken.
• ζ and δ can be obtained from d
max
. For the union
operation ζ =
d
2
and for the intersection operation
ζ = −
d
2
. δ =
d
2
.
In the same way affine forms for other functions
can be constructed. It is obvious that the affine form
can not be obtained for an arbitrary function, as the
requirements for the approximations are quite strict
and moreover the construction for the affine form can
be more computationally expensive than the natural
affine extension of the function. However, the correct
derivation of the affine form for the used functionscan
dramatically improve the speed of computations.
After the affine form computations, we obtain the
range of the function from the affine form
ˆ
f = f
0
+
f
1
ε
1
± e
f
:
f
min
= f
0
− | f
1
| − e
f
f
max
= f
0
+ | f
1
| + e
f
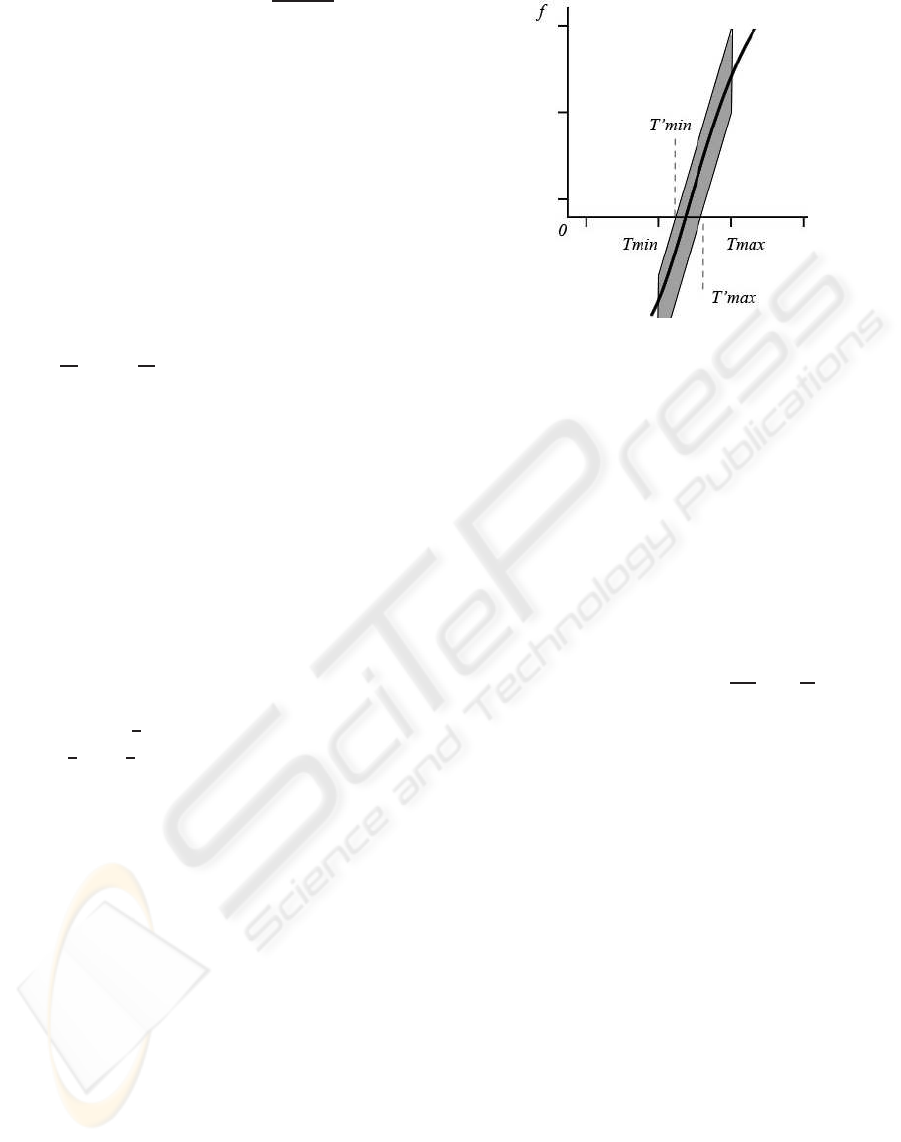
4.1.2 Argument Pruning
One of the useful properties of the reduced affine
forms, including RevAA, is that of argument prun-
ing (a term taken from the literature of interval
Figure 2: Pruning of the interval [t
min
,t
max
] to the interval
[t
′
min
,t
′
max
] after the evaluation of the revised affine form
for the function.
slope methods), which means narrowing the argu-
ment range in case the root is contained in the in-
terval. In (Gamito and Maddock, 2007b), the argu-
ment pruning formulation (the term interval optimisa-
tion is used in the paper) was suggested for Reduced
Affine Arithmetic. As the geometric meaning of the
revised affine form is similar to that of the reduced
affine form, an analogous formulation can be used as
follows. Given the revised affine form for the function
ˆ
f = f
0
+ f
1
ε
1
± e
f
for the interval
ˆ
t = t
0
+ t
1
ε
1
, pro-
viding that t
1
6= 0, f
1
6= 0 and e
f
6= 0, the interval can
be pruned by the points t
′
= t
0
−
t
1
f
0
f
1
± e
f
t
1
f
1
if these
points lie inside the interval [t
min
,t
max
] (see Fig. 2).
4.2 Implementation
In this section we present several details of the im-
plementation of ray-tracing of procedurally defined
implicit surfaces on the CPU and the GPU. The im-
plementation can be subdivided into three parts: the
RevAA representation, the function representation in
the revised affine form and the ray-tracing procedure.
4.2.1 Affine Form Representation
The value in RevAA is represented by a polynomial
with two terms and one interval. Thus, the value in
the software implementation can be represented as
a three-component vector, where the first component
represents x
0
, the second represents the noise symbol
for the error along the ray and the third represents the
half-length of the accumulating interval. The calcula-
tions in RevAA can be performed on these vectors.
Almost all of the arithmetic operations have to be
overridden as only summation in the RevAA matches
the standard vector summation. For example, subtrac-
EXTENDING REVISED AFFINE ARITHMETIC FOR FAST RELIABLE RAY-TRACING OF PROCEDURALLY
DEFINED IMPLICIT SURFACES
203

tion can be implemented as follows:
vec3 ra_subtraction(vec3 x, vec3 y){
vec3 ret;
ret[0] = x[0] - y[0];
ret[1] = x[1] - y[1];
ret[2] = x[2] + y[2];
return ret;
}
Similarly, other affine and non-affine opera-
tions can be implemented as operations on three-
component vectors. Note that for non-affine opera-
tions we are most likely to use the affine constructor
described above. In fact, any non-affine operation de-
rived for pure Affine Arithmetic with known alpha,
dzeta and delta can be adapted for RevAA.
4.2.2 Representation of the Function
The ray-tracing algorithm works with objects defined
by a real-valued functions of real-valued arguments.
In the same way this function can be rewritten by
using the following rules:
- Each variable depending on the input arguments is
replaced by a variable of the revised affine type, while
each variable not depending on the input arguments
and constants is left in the real form.
- If we have affine forms for functions or composition
of functions for the given procedural model, replace
the code over the affine variables by these forms
- Ensure that the implementation of the remaining
operations are overridden in RevAA.
The returned value of the rewritten function is
the range of the function in the affine form, which
is used in the ray-surface intersection procedure de-
scribed earlier.
4.2.3 Implementation of the Ray-tracing
Procedure
The ray-tracing procedure includes the ray-surface in-
tersection for the primary and secondary rays and
shading. The ray-surface intersection procedure de-
scribed earlier is suitable for CPU implementation,
however it can not be used in a straightforward way
for the GPU, as it is recursive. For the GPU imple-
mentation we used the version with a stack where
the information of the current argument interval is
stored. The detailed implementation of this is out-
side the scope of this paper. Another implementation
without a stack and recursion can be found in (Knoll
et al., 2009) for Interval Arithmetic, however this al-
gorithm can be easily extended for RevAA. Note that
in this implementation argument pruning can not be
(a) (b)
(c) (d)
Figure 3: Ray-tracing of algebraic surfaces: a) Bret-
zel b) Decocube; and non-algebraic implicit surfaces: c)
CSG with using blending union and blending intersection
d) Sphere with trimming.
supported and hence the speed of rendering is most
likely to be slower.
Similarly to other ray-tracing techniques for im-
plicit surfaces, we use finite differences to obtain the
normal vector for the shading and the secondary rays
calculation. Therefore the real-valued defining func-
tion of real-valued arguments should be presented as
well as the function in the revised affine form.
5 RESULTS
In our tests we used a modified version of the POV-
Ray ray-tracing software for the CPU and a stand-
alone renderer based on the GLSL language for the
GPU. The results for the CPU as well as for the GPU
implementations were generated on a PC with an In-
tel Pentium 4 3.20GHz processor and an NVidia 9600
graphics card.
GRAPP 2010 - International Conference on Computer Graphics Theory and Applications
204

(a) (b)
(c)
Figure 4: Ray-tracing of procedural implicit surfaces with
thin elements or small disjoint components: a) Sphere with
microstructure b) Sphere with procedural noise c) Procedu-
ral hair.
5.1 Offline Ray-tracing of Procedurally
Defined Implicit Surfaces
We tested our ray-tracing algorithm on a wide range
of procedurally defined implicit models (see Figs.
3, 4). First, we compare our procedure with
other reliable techniques based on uncertain computa-
tions, the technique based on Interval Arithmetic de-
scribed in (Knoll et al., 2009), the technique based
on pure Affine Arithmetic described in (de Cusatis
Jr. et al., 1999) and the technique based on Reduced
Affine Arithmetic described in (Gamito and Mad-
dock, 2007b). The results can be found in the table
1.
The results show that other rendering algorithms
based on standard Interval and Affine Arithmetic are
significantly slower than our algorithm which is based
on Revised Affine Arithmetic. The reason for this is
that with Interval Arithmetic algorithms there is an
overestimation and with Affine Arithmetic algorithms
there is an overestimation as well as a large number
of terms in the polynomial form and thus there is a
large number of arithmetic operations in the affine op-
eration calculations. Reduced Affine Arithmetic can
be used only for algebraic models and it proves to be
faster than Interval and standard Affine Arithmetic for
Figure 5: Ray tracing of procedural scenes: Virtual Shikki.
algebraic models, however the overestimation of the
function in Reduced Affine Arithmetic is wider than
the overestimation range for the Revised Affine Arith-
metic. Therefore the range of a function based on Re-
vised Affine Arithmetic is tighter than the range in
all other techniques and hence the speed of the calcu-
lation of the ray-surface intersections is significantly
better, especially for models with a large number of
non-affine operations. Also, we used special affine
forms for set-theoretic operations used in procedu-
rally defined models. The results show that the speed
increases drastically in this case.
The reliability of the Revised Affine Arithmetic
allows us to test our technique on several procedu-
rally defined implicit models with small features or
thin surfaces. For example, by using the proposed
ray-surface intersection calculation we can reliably
render models with internal structure (see Fig. 4a),
stochastic procedural models with disjointed compo-
nents (see Fig. 4b) and even procedurally-defined
hair (see Fig. 4c).
Our ray-tracing technique can be applied to com-
plex scenes with a number of procedurallydefined im-
plicit surfaces. For example, we show how a function-
ally defined scene ”Virtual Shikki” (Vilbrandt et al.,
2004) can be rendered using our technique(see Fig.
5). Note that because of the thin elements in the mod-
els approximate techniques and polygonization do not
work well for this scene.
5.2 Real-time Rendering
We tested the GPU implementation with several pro-
cedurally defined models (see Fig. 6). We compared
our technique with the technique presented in (Knoll
et al., 2009) for ray-tracing with Interval Arithmetic
and Reduced Affine Arithmetic. The results are pre-
sented in the table 2. As can be seen from the table,
RevAA gives faster ray-surface intersections – hence
the higher speed if compared with Interval Arithmetic
and near real-time frame rates for the models where
RAA is not applicable.
EXTENDING REVISED AFFINE ARITHMETIC FOR FAST RELIABLE RAY-TRACING OF PROCEDURALLY
DEFINED IMPLICIT SURFACES
205

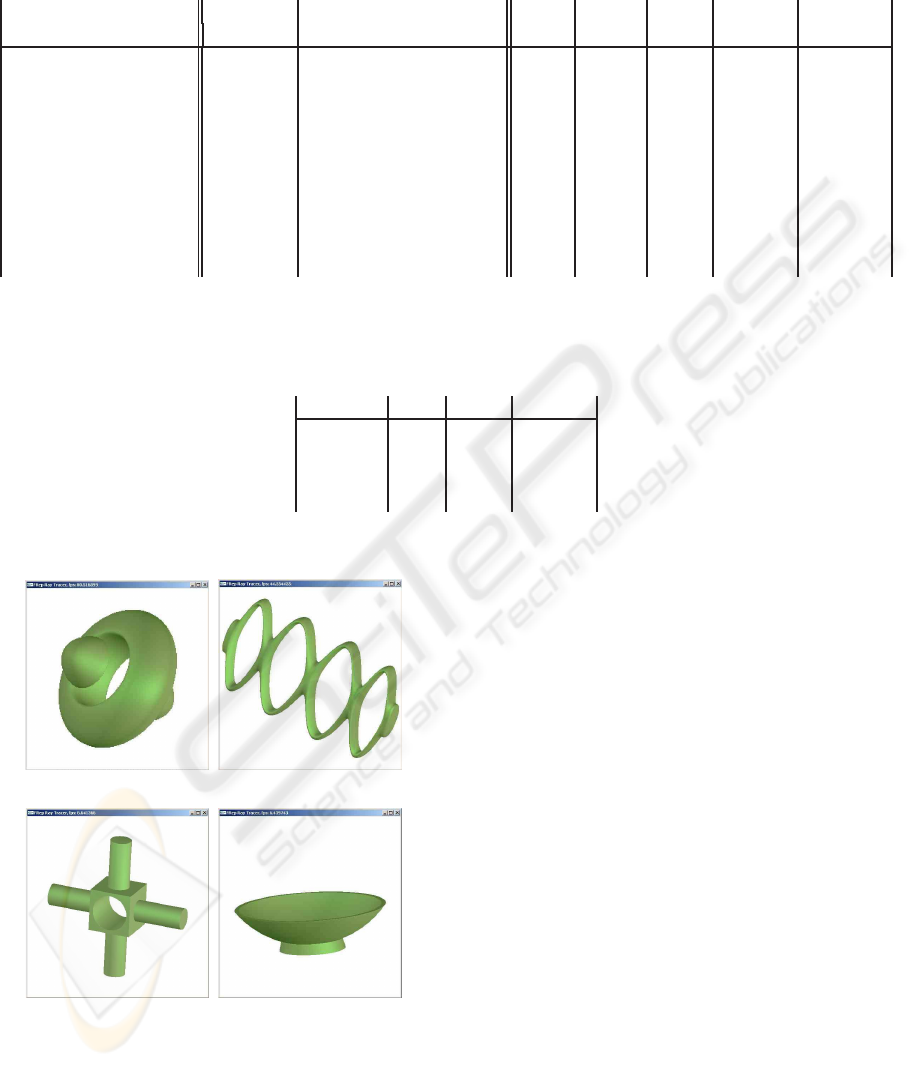
Table 1: Comparison of the ray-tracing procedures for different computational models. IA stands for Interval Arithmetic, AA
for Affine Arithmetic, RAA for Reduced Affine Arithmetic, RevAA for Revised Affine Arithmetic and RevAA* for Revised
Affine Arithmetic extended by special non-affine operations. The timings for ray-tracing all the rays are shown in seconds.
Resolution Number of operations IA AA RAA RevAA RevAA*
(pixels) All / Non-affine / Multiplications
Mitchell 1280*1024 19 / 6 / 6 38 33 7 6 6
Bretzel 1280*1024 16 / 9 / 9 25 86 22 18 18
Decocube 1280*1024 30 / 17 / 17 17 226 19 13 13
CSG 640*480 96 / 40 / 32 126 129 n/a 18 11
Sphere with trimming 1024*768 142 / 54 / 37 837 2566 n/a 285 83
Sphere with noise 800*600 36 / 11 / 5 17 51 n/a 9 9
CSG with blending 640*480 105 / 42 / 32 266 72 n/a 31 16
Hair 640*480 88 / 34 / 22 4004 1935 n/a 658 23
Sphere with microstructure 640*480 65 / 33 / 22 1006 1079 n/a 293 12
Virtual Shikki 320*240 822 / 306 / 213 29244 50000+ n/a 390 32
Table 2: Comparison of ray-casting procedures on the GPU. IA stands for Interval Arithmetic, AA for Affine Arithmetic,
RAA for Reduced Affine Arithmetic and RevAA for Revised Affine Arithmetic. All models were rendered by using only
primary rays at a resolution of 512*512 pixels. Timings are shown in FPS (frames per second) and all models were rendered
using the same camera parameters.
IA RAA RevAA
Mitchell 28.1 90.1 92.2
Bretzel 83.8 90.2 90.2
Cup 0.56 n/a 5.95
CSG 4.3 n/a 15.6
(a) (b)
(c) (d)
Figure 6: Example of real-time ray-casting using the GPU:
a) The Mitchell surface b) The Bretzel surface c) The CSG
model d) The cup model from the Virtual Shikki.
6 CONCLUSIONS
We presented a technique for ray-tracing of general
procedurally defined implicit models based on Re-
vAA. By using the inclusion property of RevAA we
were able to obtain reliable ray-tracing of models and
at the same time RevAA proved to be the fastest com-
pared to other interval techniques. We also used ar-
gument pruning to further accelerate the ray-tracing
procedure.
Currently the set of procedurally defined implicit
models does not include models with conditional op-
erators. Some research was done using Interval Arith-
metic (Diaz, 2008), however further research using
Affine Arithmetic and especially RevAA has to be
done in this area. Also in this paper we present the
affine form for set-theoretic operations based on R-
functions and show that the speed of rendering can
be dramatically improved. However, not all the func-
tions can be rewritten in the affine form and currently
there is no general criterion for the derivation of these
forms for arbitrary implicit surface models. This is
also an area that merits further research.
GRAPP 2010 - International Conference on Computer Graphics Theory and Applications
206

REFERENCES
Corrigan, A. and Dinh, H. Q. (2005). Computing and
rendering implicit surfaces composed of radial basis
functions on the GPU. In International Workshop on
Volume Graphics.
de Cusatis Jr., A., Figueiredo, L. H., and Gattass, M. (1999).
Interval methods for ray casting surfaces with affine
arithmetic. In Proceedings of SIBGRAPI’99 - the 12th
Brazilian Symposium on Computer Graphics and Im-
age Processing, pages 65–71.
de Figueiredo, L. H. and Stolfi, J. (1997). Self-Validated Nu-
merical Methods and Applications. Brazilian Mathe-
matics Colloquium monographs. IMPA/CNPq, Rio de
Janeiro, Brazil.
Diaz, J. F. (2008). Improvements in the Ray Tracing of
Implicit Surfaces based on Interval Arithmetic. PhD
thesis, Departament d’Electronica, Informatica i Au-
tomatica, Universitat de Girona, Girona, Spain.
Fryazinov, O. and Pasko, A. (2008). Interactive ray shading
of FRep objects. In WSCG’ 2008, Communications
Papers proceedings, pages 145–152.
Gamito, M. N. and Maddock, S. C. (2007a). Progressive
refinement rendering of implicit surfaces. Computers
& Graphics, 31(5):698–709.
Gamito, M. N. and Maddock, S. C. (2007b). Ray cast-
ing implicit fractal surfaces with reduced affine arith-
metic. The Visual Computer, 23(3):155–165.
Hart, J. C. (1993). Ray tracing implicit surfaces. In Sig-
graph 93 Course Notes: Design, Visualization and
Animation of Implicit Surfaces, pages 1–16.
Hart, J. C. (1994). Sphere tracing: A geometric method for
the antialiased ray tracing of implicit surfaces. The
Visual Computer, 12:527–545.
Hasan, M. (2003). An efficient F-rep visualization
framework. Master’s thesis, Faculty of Mathemet-
ics, Physics and Informatics, Comenius University,
Bratislava, Slovakia.
Knoll, A., Hijazi, Y., Kensler, A., Schott, M., Hansen, C. D.,
and Hagen, H. (2009). Fast ray tracing of arbitrary
implicit surfaces with interval and affine arithmetic.
Computer Graphics Forum, 28(1):26–40.
Martin, R., Shou, H., Voiculescu, I., and Wang, G. (2001).
A comparison of Bernstein hull and affine arithmetic
methods for algebraic curve drawing. In Proc. Un-
certainty in Geometric Computations, pages 143–154.
Kluwer Academic Publishers.
Messine, F. (2002). Extensions of affine arithmetic: Appli-
cation to unconstrained global optimization. Journal
of Universal Computer Science, 8(11):992–1015.
Mitchell, D. P. (1991). Three applications of interval anal-
ysis in computer graphics. In Frontiers in Rendering
course notes, pages 1–13.
Shapiro, V. (2007). Semi-analytic geometry with R-
functions. Acta Numerica, 16:239–303.
Sherstyuk, A. (1999). Fast ray tracing of implicit surfaces.
Computer Graphics Forum, 18(2):139–147.
Singh, J. M. and Narayanan, P. (2009). Real-time ray trac-
ing of implicit surfaces on the gpu. IEEE Transactions
on Visualization and Computer Graphics.
Snyder, J. M. (1992). Interval analysis for computer graph-
ics. In Computer Graphics, pages 121–130.
Vilbrandt, C., Pasko, G., Pasko, A. A., Fayolle, P.-A., Vil-
brandt, T., Goodwin, J. R., Goodwin, J. M., and Kunii,
T. L. (2004). Cultural heritage preservation using con-
structive shape modeling. Computer Graphics Forum,
23(1):25–42.
Vu, X.-H., Sam-Haroud, D., and Faltings, B. (2009). En-
hancing numerical constraint propagation using mul-
tiple inclusion representations. Annals of Mathematics
and Artificial Intelligence, 55(3-4):295–354.
EXTENDING REVISED AFFINE ARITHMETIC FOR FAST RELIABLE RAY-TRACING OF PROCEDURALLY
DEFINED IMPLICIT SURFACES
207