
FPGA-BASED NORMALIZATION FOR MODIFIED
GRAM-SCHMIDT ORTHOGONALIZATION
I. Sajid, Sotirios G. Ziavras
Electrical and Computer Engineering Department, New Jersey Institute of Technology, Newark, NJ 07102, U.S.A.
M. M. Ahmed
Department of Electronic Engineering, Mohammad Ali Jinnah University (MAJU), Islamabad, 44000, Pakistan
Keywords: Modified Gram-Schmidt, Orthogonalization, Normalization, FPGA.
Abstract: Eigen values evaluation is an integral but computation-intensive part for many image and signal processing
applications. Modified Gram-Schmidt Orthogonalization (MGSO) is an efficient method for evaluating the
Eigen values in face recognition algorithms. MGSO applies normalization of vectors in its iterative
orthogonal process and its accuracy depends on the accuracy of normalization. Using software, floating-
point data types and floating-point operations are applied to minimize rounding and truncation effects.
Hardware support for floating-point operations may be very costly in execution time per operation and also
may increase power consumption. In contrast, lower-cost fixed-point arithmetic reduces execution times and
lowers the power consumption but reduces slightly the precision. Normalization involves square root
operations in addition to other arithmetic operations. Hardware realization of the floating-point square root
operation may be prohibitively expensive because of its complexity. This paper presents three architectures,
namely ppc405, ppc_ip and pc_pci, that employ fixed-point hardware for the efficient implementation of
normalization on an FPGA. We evaluate the suitability of these architectures based on the needed frequency
of normalization. The proposed architectures produce a less than 10
-3
error rate compared with their
software-driven counterpart for implementing floating-point operations. Furthermore, four popular
databases of faces are used to benchmark the proposed architectures.
1 INTRODUCTION
Eigen values are used for the extraction of features
in face recognition. Their evaluation is a time
consuming but important part of pattern recognition
algorithms (Niklas, P., and Franz-Erich, etl.)
(Stavros, P, Peter, L, and Miroslaw, B.). Gram-
Schmidt orthogonalization (GSO) is fast and deals
with an orthogonal space for the computation of
Eigen values (Sharma, A., and Paliwal, K.K.).
Orthogonality usually provides better decision
power in face recognition. However, GSO may face
convergence problems with the co-variance matrix
of high-resolution images. The modified GSO
(MGSO) approach used in fast principal component
analysis (FPCA) does not increase the time
complexity while solving the convergence problem
(Sajid, I., Ahmed, M.M., and Taj, I.). However,
MGSO requires additional vector normalization.
Normalization is an essential but time consuming
part of MGSO, and is applied iteratively. Euclidian
length normalization that applies floating-point
operations may provide more accurate results in face
recognition (Sajid, I., Ahmed, M.M., and Taj, I.)
(He, X., and Yan, S etl.). But floating point
operations are costly in hardware, especially the
square root; they use more on-chip resources and
consume more cycles as compared to integer
operations (Sajid, I., Ahmed, M.M. etl.) (Oberstar,
E. L.) (Liao, J.R.) (Yamin, L., and Wanming, C.)
(Peter, S., and Mirian, L.). On the other hand, fixed-
point arithmetic hardware can be used to provide
efficient calculations with precision near that of
floating-point. The precision of fixed point depends
upon the chosen Q.N format (Wilkinson, J. H.)
(Ortega, J.M.) (Burden, R. L., and Faires, J. D.).
Normalization involves a square root operation
in addition to other arithmetic operations. A fixed-
227
Sajid I., G. Ziavras S. and M. Ahmed M. (2010).
FPGA-BASED NORMALIZATION FOR MODIFIED GRAM-SCHMIDT ORTHOGONALIZATION.
In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 227-232
Copyright
c
SciTePress

point square root operation is more time and power
efficient than its floating-point counterpart, but it
loses slightly in precision due to its algorithmic
complexity. For the sake of efficiency, non-restoring
algorithms for the fixed-point square root operation
have been implemented on FPGAs (Piromsopa, K.,
and Aporntewan, C. etl.). Non-restoring can provide
precision up to three decimal places for an operand
less than unity, which is the observed operand range
in normalization for MGSO.
Co-design methodologies are employed to
achieve trade-offs among resource utilization,
execution time and power consumption. The
software realization of Euclidian length
normalization has time complexity O (n logn)
(Stavros, P, Peter, L, and Miroslaw, B.) (Gavish, B.,
and Sridhar,S.), where n is the rank of the square
matrix. This complexity can be reduced using a co-
design process to involve fixed-point arithmetic,
pipelining and instruction-level parallelism (ILP) for
arithmetic operations (Chin-Chin, H. and Shin-Ichi,
Y. etl.) (Benkrid, K., Crookes, D. etl.).
In this paper, three novel co-design architectures
are presented that use fixed-point operations,
pipelining and ILP for vector and matrix
normalization on FPGAs. Our analysis of power
consumption and execution time for these
architectures reveals a desirable/optimal way of
implementing normalization. We validate the
proposed design methodology via benchmarking that
involves image normalization for four popular
databases of human faces. Our results show a close
to 20% improvement in execution time when using
just 3% additional power, while keeping the
precision within three decimal places which has
been proven to be adequate for face recognition with
MGSO (Giraud, L. and Langou, J. etl.).
2 ARCHITECTURES
2.1 Software Implementation: ppc405
The ppc405 architecture of three layers for matrix
and vector normalization is implemented on an
FPGA. The application layer is composed of the data
producer (DP), the data consumer (DC) and the
fixed-point normalization unit (FxN). DP and DC
are in charge of providing data to the FxN unit and
getting back data from the real-time operating
system (RTOS) layer, respectively. FxN is a
computation unit that also translates floating-point
instructions into sequences of fixed-point integer
instructions determined at compilation. To facilitate
these interactions, two FIFO queues are involved in
one-way communication. The hardware in the third
layer does not contain floating-point units (FPUs)
since it targets fixed-point operations created by
FxN. FPUs are avoided because of their high cost in
FPGA resources and per-operation large number of
machine cycles. Thus, ppc405 presents a more time
and power efficient architecture than an FPU-based
architecture. However, a pure software
implementation of the required conversion of
floating-point operations will prove much slower
compared to an implementation that utilizes
appropriate fixed-point hardware components.
Therefore, an efficient hardware implementation of
the FxN unit becomes our primary objective.
2.2 IP-based Architecture: ppc_ip
The ppc_ip presents our second architecture which is
intellectual property (IP) based. For the new
architecture, the FxN unit of Section 2.1 was
designed in the VHDL language and the name
IP_NM was assigned to it. This IP core was then
integrated into the processor local bus (PLB) of the
PowerPC core processor as IP_FxN instead of
integrating it with the on-chip peripheral bus (OPB)
of the previous architecture. IP_FxN requires pairs
of multiplication and add/subtraction operations to
be carried out in an indivisible manner, similar to
MAC (multiply-and-accumulate) operations. In
addition to the MAC operation, division and square
root operations are required as well. IP_FxN was
designed towards efficiency by considering the
architecture of the target FPGA device XC2VP30.
The fixed-point square root (FxSqr) operation is
not advisable to be implemented within IP_FxN
because FxSqr needs a dedicated implementation on
the FPGA. Nested hardware processes require stack
memory for the call back function pointer. The
alternative is to design FxSqr in a separate process
and connect it through FIFOs with IP_FxN. This
will remove the need of the stack memory and its
associated controller. The stack memory may be a
less expensive solution but its management requires
customization of the embedded core’s functionality,
a task which is cumbersome. This architecture
moves the fixed-point normalization module from
the software layer of ppc405 to the hardware layer.
This increases slightly the consumed resources. On
the other hand, it improves significantly the
execution time for desired operations which is our
primary objective. Thus, the ppc_ip architecture is
more time and power efficient than the ppc405
architecture. The resources consumed by the
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
228

hardware layer of ppc_ip can be reduced further by
appropriately eliminating the processor core from
the hardware layer.
2.3 PCI-based Architecture: pc_pci
Figure 1 presents our PCI-based FPGA architecture
without a PowerPC embedded processor core. In this
architecture, only the computational unit IP_FxN is
placed inside the FPGA device. The data producer
(DC) is implemented by a C shell on the host
machine and the PCI bus acts as the interface
between DC and the FPGA. The execution time can
be estimated using the following Equation:
ippifHex
ttttt
(1)
Where t
ex
is the execution time for the normalization
of the matrix or vector, t
H
is the time consumed by
the host application, t
if
is the time taken by the two
ends of the hardware layer for data transfers, t
p
is the
time consumed on the PCI bus and t
ip
is the time
taken by the IP core. The IP core has the same
design as in ppc_ip architecture. The two ends in
the hardware layer are: (a) the FPGA on the
Annapolis MicroSystems WildStar II-PCI board
with two Xilinx Virtex II XC2V6000-5 user-
configurable FPGAs; and (b) the software controller
at the PC OS side. The PCI bus operates at 133 MHz
and can send 32-bit data in 8 nanoseconds for a
matrix of rank 20. But usually the PCI bus takes
more time due to some acknowledgement signals
and possible packet loss overheads. It has been
observed that t
p
is about 6.4 microseconds for a
square matrix of rank 20. On the other hand, t
H
dominates in Equation (1) for this architecture
because the respective process executes in a C shell
on the PC. This architecture uses the minimum
resources on the FPGA because it does not require
FIFOs and an embedded core. Furthermore, it could
be beneficial to improve the FPGA frequency
sufficiently, so that the ratio of t
H
to other terms can
be reduced.
3 EXPERIMENTS, RESULTS AND
COMPARATIVE ANALYSIS
The accuracy of normalization depends upon Q.N
format and values of the matrix elements. The
proposed architectures were designed for the
normalization of matrices used in face recognition
tasks. In this regard, four popular databases with
human faces have been selected to validate our
design methodology. They are the Yale, Olivetti
Research Laboratory (ORL), Feret database and
CAS-PEAL databases (Yale Database) (Face
Database) (Wen,G., and Bo, Ce. etl.) (Phillips, P. J.,
Moon. etl.).
The Yale faces database contains 165 images of
15 subjects, with 11 images per subject. The ORL
faces database contains 400 images of 40 personnel.
These images have different variations in facial
expression, like open or closed eyes, smiling or non-
smiling, and facial details such as with glasses or
without glasses. CAS-PEAL is a Chinese faces
database containing 99,594 images of 1040 subjects.
A total of nine cameras were used to simultaneously
capture images across different poses, facial
expressions, lighting and angles. Feret is a big
database containing 14,126 images of 1199 subjects.
The performance of the proposed architectures is
judged based on the parameters of accuracy,
execution time and power consumption. A set of
twenty randomly selected images from the four
databases were tested to investigate the performance
of our implementations. The images in these four
databases were captured with different resolutions.
To measure the accuracy of the implementations,
the root mean square (RMS) metric is used. Initially,
values are recorded using the proposed fixed-point
arithmetic system with Matlab for the IEEE754
double-precision floating-point standard. The
minimum, maximum and average RMS values are
calculated for the said databases as shown in Figure
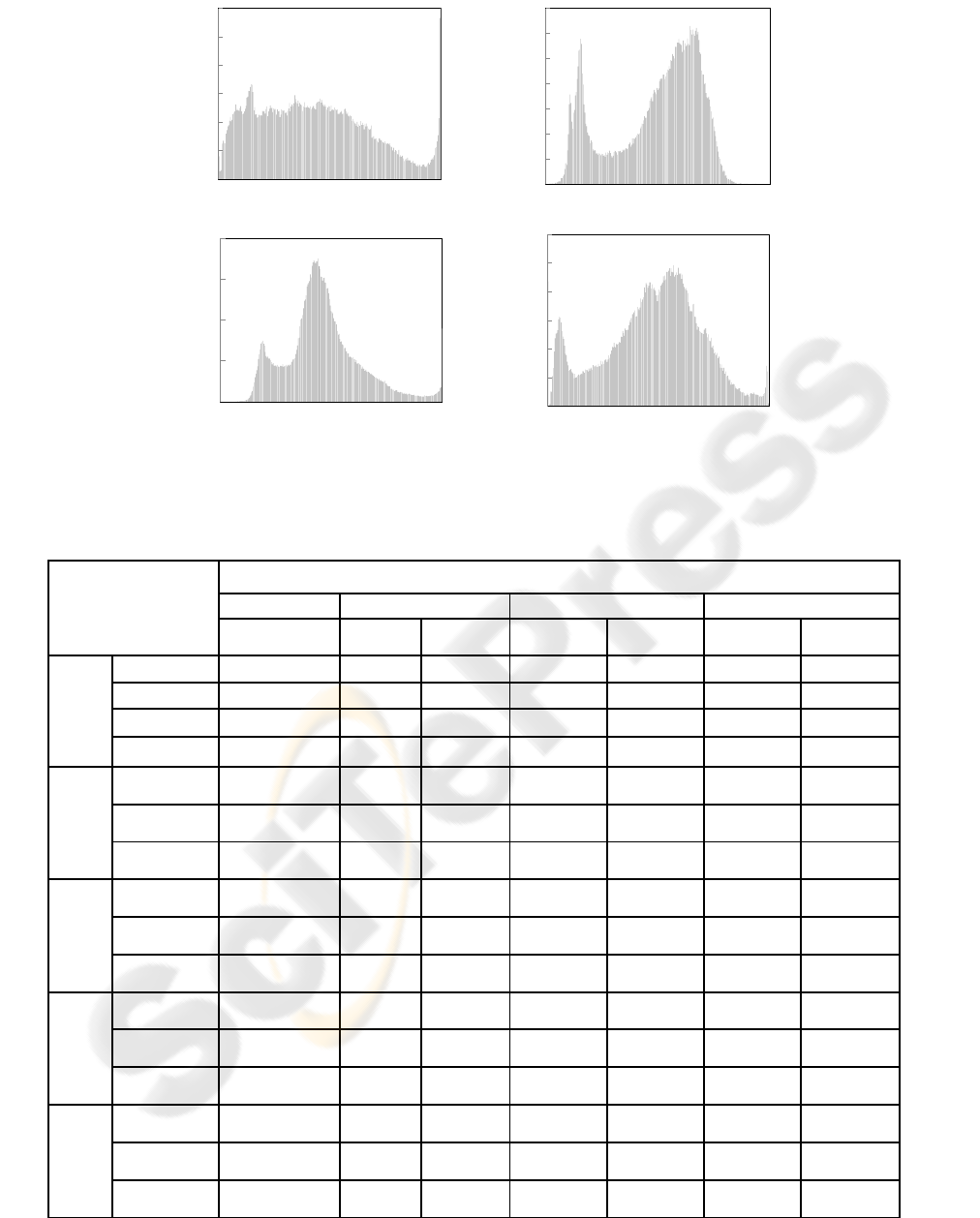
2. In Figure 2, the highest error is produced by Yale
whereas the minimum RMS error is for Feret. The
average histograms of gray levels for randomly
selected images from these databases could reveal
the error variation in the proposed system. The
Feret-based histogram shows a relatively close to
normal Gaussian distribution curve as shown in
Figure 3. Figure 3 shows average histogram of
twenty images from the said databases. Gaussian
distribution of pixel values suits our proposed
approach because truncation errors due to the least
significant digits are small. CAS-PEAL also follows
the Gaussian curve but its frequency of peaks is low
compare to Feret. On the other hand, ORL and Yale
have the smallest distribution of values in the central
region than Feret and CAS_PEAL. Furthermore
their maximum frequency of central region is
smaller than Feret and CAS-PEAL. The RMS error
range for all the databases is on the order of 10
-3
as
shown in Figure 2, which is quite acceptable for face
recognition using MGSO.
FPGA-BASED NORMALIZATION FOR MODIFIED GRAM-SCHMIDT ORTHOGONALIZATION
229

PC OS Layer
FPGA
xc2vp30ff896c
Data Producer (DP)
Input Matrix
Data Consumer
(DC)
Normalized
Matrix
PCI
Hardware layer
Application layer
32-bits fixed point
Square root
IP_FxN
Fixed point
Normalization
Figure 1: pc_pci architecture.
Table 1 shows the execution time and power
dissipation comparison of our architectures
presented in Section 2. The architectures were
evaluated based on their required FPGA resources
and the time taken to complete the normalization
process. The power dissipation was estimated using
Xilinx data sheets and the Xilinx XPower tool in the
integrated simulation environment (ISE). The
execution time for software processes was noted
using the Xilinx embedded development kit (EDK)
and the execution time of IP_FxN was estimated
using the synthesis report. FIFOs and the PCI bus
were used for communication purposes. The FIFOs
were implemented in hardware and were
incorporated in the IP_FxN module. The PCI bus is
not part of IP_FxN in pc_pci. Therefore, the time
taken by pc_pci is on the higher side compared to
ppc_ip. The PCI time depends upon the
specifications of the host machine.
In Table 1, ppc405. ppc_ip and pc_pci are the
architectures proposed in Sections 2.1, 2.2 and 2.3,
respectively. ppc405 cannot be implemented using
pipelining and ILP techniques because this
architecture uses Fx_N in the software layer. The
ppc_ip and pc_pci architectures were implemented
with pipelining and loop unrolling (ILP) techniques.
Therefore, seven implementation scenarios can be
seen in Table 1. Architectures employing pipelining
and ILP are more time efficient than the same
architectures without pipelining and ILP. On the
other hand, the maximum power is consumed by
ppc_ip (PL_ILP) and the minimum power by pc_pci
(WPL). The data feeding time for the ppc405 and
ppc_ip architectures is consumed by the DP
component; in the case of the pc_pci architecture,
this time is consumed by the PCI bus and the DP
unit. The bandwidth of the PCI bus depends upon
the host machine. However, the PCI bus time is sig-
nificantly high compared to using DP.
Figure 2: Error Analysis of fixed-point normalization for
the four databases.
In MGSO, approximately 4000 normalization
operations are required for a matrix of rank 20. The
ppc_ip (PL_ILP) architecture consumes the
minimum execution time for a matrix of rank 20.
But a matrix of rank 200 requires approximately a
fraction of a million normalization operations to
complete MGSO. In this situation, the ppc_ip
(PL_ILP) and pc_pci (PL_ILP) architectures
consume almost similar execution times. On the
other hand, pc_pci (PL_ILP) consumes 62% less
power than the ppc_ip (PL_ILP) architecture. Most
of the image and signal processing applications
require thousands of thousands of normalization
operations. Thus, pc_pci (PL_ILP) proves to be the
optimal solution for FPGA-based normalization
considering the accuracy, execution time and power
consumption.
Moments, which are projections of the image
function to the basis function, are used in object
tracking. High speed normalization of moments has
been has been implemented on the XCV1000 device
using parallel accumulators. It resulted in a
maximum calculation of 190 frames per second for
images having resolution 512x512 (Stavros, P, Peter,
L, and Miroslaw, B.). On the other hand, the
proposed architecture using a smaller XC2V30P
device produces 190 frames for the same resolution
in 0.116 seconds. Our system operates
approximately nine times faster than the one
proposed in (Stavros, P, Peter, L, and Miroslaw, B.).
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
230
0
20
40
60
80
100
120
1
51
101
151
201
251
Frequency
Gray Level
Yale
0
10
20
30
40
50
60
70
1
51
101
151
201
251
Frequency
Gray Level
ORL
0
100
200
300
400
1
51
101
151
201
251
Frequency
Gray Level
Feret
0
20
40
60
80
100
120
1
51
101
151
201
251
Frequency
Gray Level
CAS-PEAL
Figure 3: Average histogram of twenty images from four face databases.
Table1: Comparisons of execution time, and resource and power consumptions for the XC2VP30ff896c FPGA
XC2VP30ff896c FPGA.
Architectures
Software-Based
Unpipelined (WPL)
Pipelined (PL)
PL_ILP
Performance
Parameters
PPC405
PPC_IP
PC_PCI
PPC_IP
PC_PCI
PPC_IP
PC_PCI
Resources
Slices
1979
4587
1750
4615
1765
4641
1794
LUTs
2266
7399
3402
7471
3443
7514
3489
Flip-flops
1981
2709
930
2710
936
2900
1157
mWatts
5.78
13.39
5.11
13.48
5.15
13.55
5.24
Exec. Time (1
Oper)
Data feeding
time (µs)
346.28
346.28
15064
346.28
15064
346.28
15064
Exec.
Time(µs)
232.15
11.3
13.2
11.11
12.15
9.32
9.32
Total time
(µs)
578.43
357.58
15077.2
357.385
15076.2
355.6
15073.3
Exec. Time
(1000 Oper)
Data feeding
time (µs)
346.28
346.28
15064
346.28
15064
346.28
15064
Exec.
Time(µs)
232148.32
11295
13200
11105
12150
9320
9320
Av. Time
(µs)
232.49
11.64
28.26
11.45
27.21
9.67
24.38
Exec. Time
(10
6
Oper)
Data feeding
time (µs)
346.28
346.28
15064
346.28
15064
346.28
15064
Exec.
Time(µs)
2.32E+10
1.12E+08
1.32E+07
1.10E+07
1.20E+07
9.32E+06
9.32E+06
Av. Time
(µs)
232.15
11.3
13.22
11.1
12.17
9.32
9.33
Exec. Time (10
8
Oper)
Data feeding
time (µs)
346.28
346.28
15064
346.28
15064
346.28
15064
Exec.Time
(µs)
2.32E+10
1.13E+08
1.32E+08
1.10E+08
1.20E+08
9.32E+07
9.30E+07
Av. Time
(µs)
232.14833
1.129504
1.32
1.1105
1.21515
0.932004
0.93215
FPGA-BASED NORMALIZATION FOR MODIFIED GRAM-SCHMIDT ORTHOGONALIZATION
231

4 CONCLUSIONS
Three layers for three FPGA-based architectures
were proposed targeting at the normalization of a
matrix or vector. These architectures were designed
and analyzed on the basis of accuracy, execution
time and power consumption. The impact of
pipelining and instruction level parallelism was
studied as well using an architecture co-design
methodology. The host-to-PCI based architecture
provides an optimum combination of accuracy,
processing time and power consumption. The pc_pci
architecture provides a more than 200 times faster
solution than the software-based solution running on
an embedded system and is 62% more efficient than
the IP-based architecture. Furthermore, this
architecture is about nine times faster than a
previously proposed architecture while also yielding
an accuracy of within 10
-3
as compared to a
hardware-based floating-point architecture.
REFERENCES
Benkrid, K., Crookes, D., Bouridane, A., Con, P., and
Alotaibi, K., 1999, A High Level Software
Environment for FPGA Based Image Processing,
Image Proc. And Its Applications. Seventh Inter.
Conf., Manchester, U.K.
Burden, R. L., and Faires, J. D., 2005. Numerical
Analysis, seventh ed., Thomson.
Chin-Chin, H., Shin-Ichi, Y., 1996. Hideji Fujika, W., and
Koichiro, S., A Fuzzy Self-Tuning Parallel Genetic
Algorithm For Optimization, Computers ind. Engng
vol. 30, no. 4.
Gavish, B. and Sridhar,S., 2006. “Computing the 2-
median on tree networks in O (n lg n) time, Inter.
Jour. of networks, vol. 26, issue 4, Wiley InterScience.
Giraud, L., Langou, J. and Rozloznik, M., 2003. On the
loss of orthogonality in the Gram-Schmidt
orthogonalization process, Technical Report
TR/PA/03/25, CERFACS.
He, X., Yan, S., Hu, Y., Niyogi, P., and Zhang, H., 2005.
Face Recognition Using Laplacian faces”, IEEE
Trans. on Pat. Anal and Machine Intelligence, vol. 27,
no. 3.
IBM 64-bit processor local bus architecture specification
version 3.5, patent no. SA-14-2534-01, May, 2001.
Liao, J.R., 2000. Real-Time Image Reconstruction for
Spiral MRI Using Fixed-Point Calculation, IEEE
Trans. on Medical Imaging, vol. 19, no.7.
Niklas, P., Franz-Erich, W. and Martin, R., 2007. Laplace
spectra as fingerprints for image recognition,
Computer Aided Design, vol. 39.
Oberstar, E. L., 2007. Fixed-point representation &
fractional math, Report Oberstar Consulting.
Ortega, J.M., 1963. An Error Analysis of Householder's
Method for the Symmetric Eigenvalue Problem”,
Numerische Mathematik, 1-225.
Peter, S. and Mirian, L., 1996. Area and Performance
Tradeoffs in Floating-point Divide and Square-Root
Implementations, ACM Comp. Sur., vol. 28, no. 3.
Piromsopa, K., Aporntewan, C., and Chongsatitvatana, P.,
2009. An FPGA Implementation of a Fixed-point
Square Root Operation, ISCIT, 2001.
Phillips, P. J., Moon, H., Rizvi, S. A., and Rauss, P. J,
2000. The Feret Evaluation Methodology for Face-
Recognition Algorithms”, IEEE Trans. Pat. Anal.
Mach. Intell., vol. 22, no. 10.
Sajid, I., Ahmed, M. M. and Sageer, M., 2010 PGA based
optimized architecture for face recognition using fixed
point Householder algorithm, Acceptance for
publication, VI South. Prog. Logic Conf., Brazil.
Sajid, I., Ahmed, M. M., and Taj, I., 2009. Time Efficient
Face Recognition Using Stable Gram-Schmidt
Orthonormalization, Inter. Jour of Signal and Image
Proc. and Pat. vol. 1, no.2.
Sajid, I., Ahmed, M. M., Taj, I., Humayun, M., 2008.
Design of High Performance FPGA based Face
Recognition System, Proc. of Prog. In Electro.
Stavros, P, Peter, L, and Miroslaw, B, 2003. An FPGA
System for the High Speed Extraction, Normalization
and Classification of Moment Descriptors, Lecture
notes in computer science, 2003 - Springer.
Sharma, A., and Paliwal, K. K., 2007. Fast principal
component analysis using fixed-point algorithm, Patt.
Recog. Letters, vol. 28, no. 10.
The Database of Faces at a glance, 2009.
http://www.cl.cam.ac.uk/research/dtg/attarchive/facesatagl
ance.html.
Wilkinson, J. H., 1962. Error Analysis of Eigenvalue
Techniques Based on Orthogonal Transformations,
Journal of the Society for Industrial and Applied
Mathematics, vol. 10, no. 1.
Wen,G., Bo, C., Shiguang, S., Xilin, C., Delong, Z.,
Xiaohua, Z., and Debin, Z., 2008. The CAS-PEAL
Large-Scale Chinese Face Database and Baseline
Evaluations, IEEE Trans. Systems, man, and
cybernetics—part a: systems and humans, vol. 38, no.
1, JANUARY http://www.jdl.ac.cn/peal/index.html
Yamin, L., and Wanming, C., 1997. Implementation of
Single Precision Floating Point Square Root on
FPGAs, Proceeding of the 5th IEEE symposium on
FPGA-based custom computing Machines, April
http://www.superkits.net/whitepapers.htm.
Yale Univ. Face Database, 2002
http://cvc.yale.edu/projects/yalefaces/yalefaces.html.
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
232
