ROAD CRACK EXTRACTION WITH ADAPTED FILTERING AND

MARKOV MODEL-BASED SEGMENTATION

Introduction and Validation

S. Chambon, C. Gourraud, J.-M. Moliard and P. Nicolle

Laboratoire Central des Ponts et Chausses, LCPC, Nantes, France

Keywords:

Fine structure extraction, Evaluation and comparison protocol, Matched ﬁlter, Markov model, Segmentation.

Abstract:

The automatic detection of road cracks is important in a lot of countries to quantify the quality of road surfaces

and to determine the national roads that have to be improved. Many methods have been proposed to automat-

ically detect the defects of road surface and, in particular, cracks: with tools of mathematical morphology,

neuron networks or multiscale ﬁlter. These last methods are the most appropriate ones and our work con-

cerns the validation of a wavelet decomposition which is used as the initialisation of a segmentation based on

Markovian modelling. Nowadays, there is no tool to compare and to evaluate precisely the peformances and

the advantages of all the existing methods and to qualify the efﬁciency of a method compared to the state of the

art. In consequence, the aim of this work is to validate our method and to describe how to set the parameters.

1 INTRODUCTION

In many countries, the quality of roads is evalu-

ated by taking into account numerous characteristics:

adherence, texture and defects. Since 1980, many

efforts have been spent for making this task more

comfortable, less dangerous for employees and also,

more efﬁcient and less expensive by using an acquisi-

tion system of road images and by introducing semi-

automatic defect detection, in particular crack detec-

tion. Nowadays, a lot of acquisition systems are pro-

posed, see (Schmidt, 2003), but, as far as we are con-

cerned, even if a lot of automatic crack detections had

been proposed, no method had been widely applied.

In fact, this problem is difﬁcult because road cracks

represent a small part of the images (less than 1.5%

of the image) and is very low contrasted (the signal

of the crack is mixed with the road texture). Actu-

ally, there is no evaluation protocol to compare and to

highlight methods that are well dedicated to this task

and we propose to introduce such a protocol. More-

over, our second aim is to introduce and to validate

our contributions about a multi-scale approach based

on two steps: a binarization with adapted ﬁltering and

a reﬁnement of the binarization by a Markov model-

based segmentation.

First, existing methods are resumed before describing

our approach. Then, we introduce the evaluation pro-

tocol that enables us to validate the new approach and

we give the details of the parameter settings.

2 DETECTION OF ROAD

CRACKS

For this task, three steps can be distinguished: image

acquisition, data storage and image processing. In this

paper, even if the choices for the two ﬁrst steps are

important, we focus on the image processing step.

Four different kinds of methods exist, see Table 1.

The thresholding methods are the oldest ones and also

the most popular. They are based on histogram analy-

sis (Acosta et al., 1992), on adaptive thresholding (El-

behiery et al., 2005), or on Gaussian modelling (Kout-

sopoulos and Downey, 1993). These techniques are

simple but not very efﬁcient: the results show a lot of

false detections. Some methods are based on morpho-

logical tools (Elbehiery et al., 2005; Iyer and Sinha,

2005; Tanaka and Uematsu, 1998). The results con-

tain less false detections but they are highly depen-

dent on the choice of the parameters. Neuron net-

works-based methods have been proposed to alleviate

the problems of the two ﬁrst categories (Kaseko and

Ritchie, 1993). However, they need a learning phase

which is not well appropriate to the task. Filtering

Chambon S., Gourraud C., Moliard J. and Nicolle P. (2010).

ROAD CRACK EXTRACTION WITH ADAPTED FILTERING AND MARKOV MODEL-BASED SEGMENTATION - Introduction and Validation.

In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 81-90

DOI: 10.5220/0002848800810090

 SciTePress

methods are the most recent. At the beginning, a con-

tour detection has been used but the major drawbacks

lie on using a constant scale, supposing that the width

of the crack is constant and that we suppose that the

background is not as noisy (or textured) as a road sur-

face. This is not realistic and this is why, most of the

ﬁltering methods are based on a wavelet decomposi-

tion (Delagnes and Barba, 1995; Subirats et al., 2006;

Wang et al., 2007; Zhou et al., 2005) or on partial dif-

ferential equations (Augereau et al., 2001). We can

also notice an auto-correlation method (Lee and Os-

hima, 1994) (the authors estimate a similarity coefﬁ-

cient between patterns that represent simulated cracks

and patterns inside the images). Some methods also

use texture decomposition (Petrou et al., 1996; Song

et al., 1992) (the goal is to ﬁnd a noise, i.e. the crack,

inside a known texture).

Table 1: State of the art about road crack detection – In

brackets, we give the years of publication.

THRESHOLD

(1992–1999)

(Acosta et al., 1992; Cheng

et al., 1999; Koutsopoulos and

Downey, 1993)

MORPHOLOGY

(1998)

(Tanaka and Uematsu, 1998)

NEURAL

NETWORK

(1991–2006)

(Bray et al., 2006; Chou et al.,

1995; Kaseko and Ritchie,

1993; Ritchie et al., 1991)

MULTI-

SCALE

(1990–2009)

(Chambon et al., 2009;

Delagnes and Barba, 1995;

Fukuhara et al., 1990; Subirats

et al., 2006; Zhou et al., 2005)

3 AFMM METHOD

First, we present the general algorithm of the method:

Adapted Filtering and Markov Model-based segmen-

tation (AFMM) and, second, our contributions in each

of the parts of this algorithm.

3.1 Algorithm

The goal of this algorithm, presented in Figure 1, is

to obtain, steps 1 to 3, a binarization (black pixels

for background and white pixels for the crack) and

a reﬁnement of this detection by using a Markovian

segmentation, step 4,. In the ﬁrst part, a photometric

hypothesis is used: a crack is darker than the back-

ground (the rest of the road pavement) whereas, in

the second part, a geometric hypothesis is exploited:

a crack is composed of a set of connected segments

with different orientations. The number of scales for

the adapted ﬁltering has to be chosen and depends on

the resolution of the image. By supposing a resolution

of 1 mm per pixel, by choosing 5 scales, a crack with a

width from 2 mm to 1 cm can be detected. Moreover,

the number of directions (for the ﬁltering) also has

to be chosen and, it seems natural to take these four

directions: [0,

3π

] that correspond to the four

usual directions used for crack classiﬁcation. Adapted

ﬁltering is applied in each scale, each directions and

then all the results are merged (mean of the coefﬁ-

cients). The results of this ﬁltering is used to initialize

the Markov model.

Input

Road images

Initialization

Number of scales and angles

Steps

1. For each scale do Estimate adapted

filter (AF)

2. For each direction do Apply AF

3. Merge AF in all the directions

4. For each scale do

(a) Initialize the sites (Markov)

(b) While not (stop condition) do

Update the sites

Figure 1: Algorithm with adapted ﬁlter and Markovian

modelling (AFMM) – Steps 1 to 3 lead to a binary image

using adapted ﬁltering, while step 4 reﬁnes this result with

a Markovian modelling.

3.2 Adapted Filtering

The ψ ∈ L

(IR

) function is a wavelet if:

|Ψ(x)|

kxk

dx < ∞,avec x = (i, j), (1)

where Ψ is the Fourier transform of ψ. The equa-

tion (1) induces that

ψ(x)dx = 0. The wavelet

family is deﬁned for each scale s and for each posi-

tion u, by :

x, ˆu,θ

(x) =

ψ(R

((x−u)/s)), (2)

where ψ ∈ IR

and R

is a rotation of angle θ. One

of the main difﬁculties to apply a wavelet decompo-

sition is the choice of the mother wavelet ψ. Nu-

merous functions are used in the literature: Haar

wavelet, Gaussian derivatives, Mexican hat ﬁlter,

Morlet wavelet. It is very hard to determine which

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

one is the best for a given application. In the case of

crack detection, two elements are present: the crack

(if there is a crack) and the background (the road

surface can be viewed as a repetitive texture). The

goal of the crack detection is to recognize a signal,

i.e. the shape is known up to a factor, mixed with

a noise whose its characteristics are known. Con-

sequently, adapted ﬁltering is well designed for the

problem: extracting singularities in coefﬁcients esti-

mated by a wavelet transform. If s is a discrete and

deterministic signal with values stored in the vector

s =



... s



, N the number of samples, and

z =



... z



, is a noisy observation of s, supposed

to be an additive noise: z = s+b. The main hypothe-

sis is that this second-order noise is centered and sta-

tionary, with auto-correlation function φ

of terms

(i, j)

= φ

|i−j|

, independent from the signal s. The

adapted ﬁlter h of s is deﬁned by:

h = φ

−1

s. (3)

The crack signal depends on the deﬁnition of the

crack. In this paper, like most of the papers of this

domain, crack pixels correspond to black pixels sur-

rounded by background pixels (road pixels). This is

why, in (Subirats et al., 2006), a crack is a piecewise

constant function:

f(x) =

(

−a If x ∈ [−

]

0 Elsewhere,

(4)

where the factor a and the threshold T have to be de-

termined. It does not correspond to a realistic rep-

resentation of the crack. Because of sub-sampling,

lights, orientation of the camera, the signal is more

like a Gaussian function with zero mean:

f(x) = −a e

−

(

)

, (5)

where a is the size of the crack and depends on σ,

the deviation of the Gaussian law, i.e. a =

√

(2π)

Consequently, the term σ allows to ﬁx the width of

the crack (like threshold T in equation (4)).

3.3 Contribution to Segmentation

The goal of this part is to extract shapes, i.e. cracks,

using the detection maps estimated at the ﬁrst stage

of the algorithm. The MRF (Markov Random Field)

principle is introduced before the presentation of the

improvements about the initialization of sites and the

updating of the Markov Random Field.

For the ﬁrst step of segmentation (initialization),

in (Subirats et al., 2006), the sites are of size 3 ×3,

consequently, a regular grid is considered in the im-

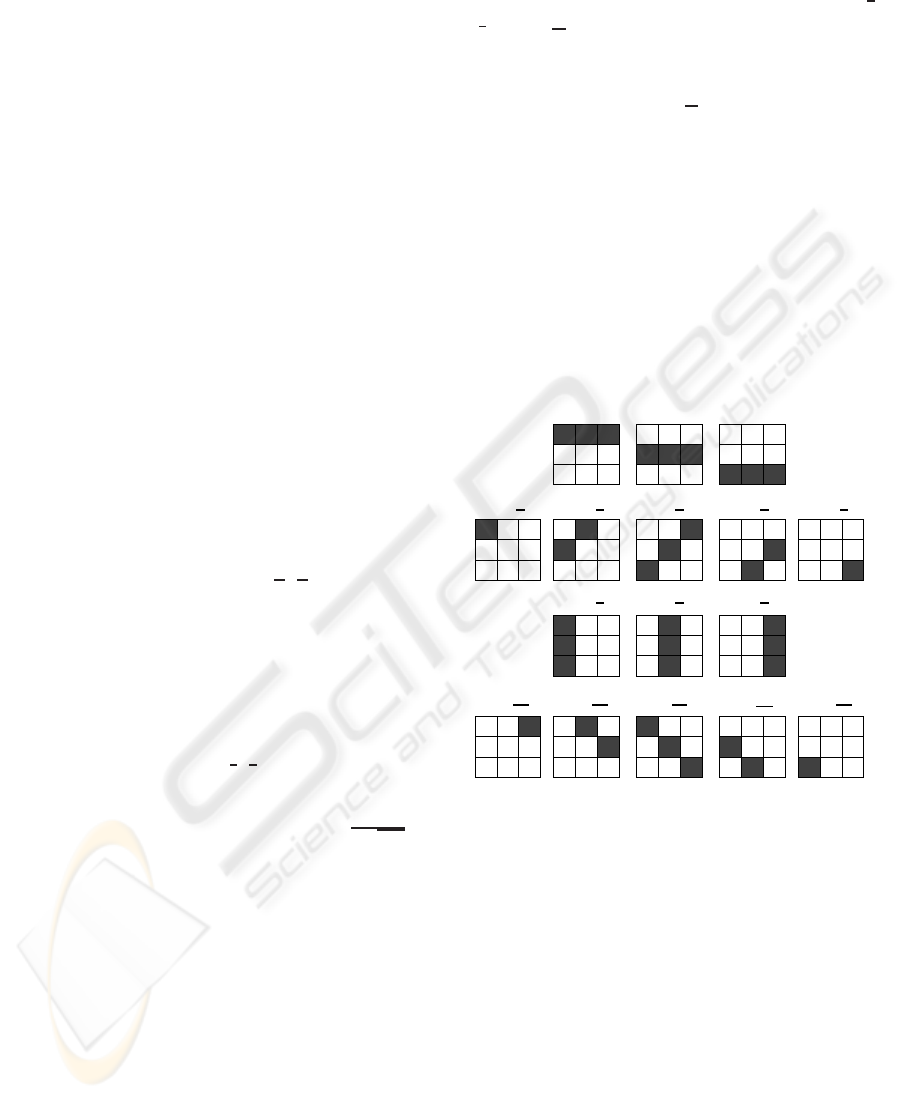
age. The four conﬁgurationsthat are possible, are rep-

resented in Figure 2. The initialization of the sites is

based on the conﬁguration that maximizes the wavelet

coefﬁcients. More formally, if we denoted γ

2,0

, γ

and γ

3π

, see in the bold rectangle in Figure 2,

the four conﬁgurations, the best conﬁguration γ

best

is:

best

= argmax

α∈

[

0..

3π

]

2,α

, (6)

where m

2,α

is the mean of wavelet coefﬁcients on the

considered conﬁguration γ

2,α

. These four conﬁgura-

tions do not represent all the possible and are not re-

alistic conﬁgurations. In fact, all these four conﬁg-

urations are centered, whereas, it is possible to have

some non-centered conﬁgurations. Consequently, we

use a set of conﬁgurations that includes this aspect

and we employ a set of sixteen conﬁgurations illus-

trated in Figure 2. By modifying the number of con-

ﬁgurations, we need to adapt the initialization of sites,

i.e. equation (6).

3ψ

3π

1,0

3,0

2,0

Figure 2: The sixteen conﬁgurations of the Markov model

(initialization) – The sites are represented with dark gray

levels.

The image is considered as a ﬁnite set of sites denoted

S = {s

,... , s

}. For each site, the neighborhood is

deﬁned by: V

′

|s /∈ V

′

& s

′

∈ V

⇒ s ∈V

′

A clique c is deﬁned as a subset of sites in S where

every pair of distinct sites are neighbors.

The random ﬁelds considered are:

1. The observation ﬁeld Y = {y

} with s ∈ S . Here,

is the mean of wavelet coefﬁcients on the site.

2. The descriptor ﬁeld L = {l

} with s ∈ S . For this

work, if there is a crack l

= 1 elsewhere l

= 0.

MRF model is well suited to take into account spatial

dependencies between the variables. Each iteration,

a global cost, or a sum of potentials, that depends on

ROAD CRACK EXTRACTIONWITH ADAPTED FILTERING AND MARKOV MODEL-BASED SEGMENTATION -

Introduction and Validation

the values of the sites and the links between neigh-

borhoods, is updated. This global cost takes into ac-

count the site coefﬁcients(computed from the wavelet

coefﬁcients estimated during the ﬁrst part of the al-

gorithm: adaptive ﬁltering) and the relation between

each site and the sites in its neighborhood (in this pa-

per, it corresponds to the eight neighbors). More for-

mally, the global cost is the sum of all the potentials

of the sites and contains two terms:

(s) = α

(s) + α

∑

′

∈V

(s,s

′

), (7)

where V

is the neighborhood of site s. The choice

of the values α

and α

depends on the importance of

each part of the equation (7).

The function u

is given by:

= 1) =

(

(k−y

)

If y

≥ k

1 Elsewhere

and

= 0) =

(

−k)

If y

< k

1 Elsewhere,

(8)

The parameters ξ

, ξ

and k have to be ﬁxed

. For

the deﬁnition of u

, we have to determine the num-

ber of cliques. In (Subirats et al., 2006), four cliques

are possible. As there is four conﬁgurations in the

previous approach, there is sixteen possibilities. A

8-neighborhood is considering but the potential func-

tion proposed in the precedent work only considers

the difference of orientations between two neighbor-

hoods and not the position between the two sites of

the clique, see Table 2.

Table 2: Function u

– This table represents the values of

the function u

′

,s) for the four initial conﬁgurations of

the sites. In the experiments we have taken the values of the

parameters proposed by the authors (Subirats et al., 2006)

and that give the best results: β

= −2, β

= −1 and β

= 2.

2,0

3π

2,0

3π

Some cases are not penalized with the old conﬁg-

uration. For example, these two unfavorable cases are

The choice of k is related to the maximal number of

pixels that belong to a crack (it depends on the resolution of

images and hypothesis about the size and conﬁguration of

cracks). We have chosen k in order to consider at most 5%

of the image as a crack. Moreover, our experimentations

have brought us to take ξ

=ξ

=100.

not penalized: two sites with the same orientation but

with no connection between them, two sites with the

same orientation but their position makes them par-

allel. This is why, with the sixteen possible conﬁg-

urations presented in Figure 2, the new variant takes

into account differences of orientations between two

sites (there are 16×16 possibilities) and position of

the two sites (there is eight possibilities because of 8-

connexion). Consequently, the new potential function

follows these two important rules:

) The lower the difference of orientations between

two sites, the lower the potential.

) The lower the distance between two sites, the

lower the potential (in this case, distance means

the minimal distance between the extremities of

the two segments).

More formally, if d denotes the Euclidean distance

between the two closest extremities of the sites, with

d ∈ [0, d

max

] (d

max

= 5

√

2), θ

and θ

, the ori-

entations of respectively s = {s

}

i=1..N

, and s

′

}

j=1..N

′

and θ

the angle between the two sites,

the u

function is deﬁned by:

′

,s) = α



|2θ

−θ

2π



(1−α

)



J(NbC) min

i, j

(d(s

′

))

max

−

NbC



(9)

where NbC indicates the number of elements of the

two sites s and s

′

and J(x) equals 1 if NbC = 0 and 0

elsewhere. The ﬁrst term is induced by the rule about

the orientations, rule (R

), it is zero when the sites

have the same orientation and this orientation is the

same as the orientation between the sites, i.e. θ

= θ

. It gives bad costs to conﬁgurations where

the sites do not have the same orientation but also the

particular case where they are parallel, see example

(a) in Figure 3. The second and third terms express

the rule (R

) about the distances. Two aspects have

to be distinguished: the number of connected pixels,

when the sites are connected, and, on the contrary,

the distance between the sites. It allows to give low

inﬂuence to disconnected sites and also to increase

the cost of sites that are parallel but connected, see

example (b) in Figure 3. To study the inﬂuence of all

these terms, the equation has been normalized and the

different terms have been weighted.

4 EVALUATION PROTOCOL

For the evaluation of automatic crack detection, there

is no evaluation and comparison protocol proposed in

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

(a) (b)

= θ

, θ

= 0, θ

and

For s

: u

−0+ 2

For s

: u

= 0−1+ 0

For s

: u

−1+ 0

= θ

= 0, θ

= θ

For s

: u

= π−3+ 0

For s

: u

= 0−1+ 0

For s

: u

= 0−0+ 2

Figure 3: Illustration of function u

– These two examples

of sites with their respective neighborhoods show the be-

havior of potential u

with the two considered aspects: ori-

entation and distance. In example (a), with the help of the

orientation term, the conﬁguration s

is penalized and s

less penalized than s

. In example (b), with the help of the

two terms on distance, the site s

is penalized, compared to

. On the contrary, the particular case of s

is favorable and

it equilibrates the penalty given by the orientations.

the community. However, in all the countries, for es-

timating the quality of the road surface, it is impor-

tant to know exactly the size and the width of the de-

fects, i.e. to detect precisely the defect. This is why,

it seems important to characterize quantitatively the

performance of the methods. For building this kind

of protocol, it is necessary, ﬁrst, to choose the tested

images, second, to choose how to build reference seg-

mentations, and, third, to determine the criteria used

for the quantitative analysis.

4.1 Tested Images

The most difﬁcult is to propose images with a ref-

erence segmentation or a ”ground truth” segmenta-

tion. On the ﬁrst hand, we create synthetic images

with a simulated crack. As shown in ﬁgure 4, the re-

sult is not enough realistic and, on the second hand,

we have taken a real image with no defect and we

have added a simulated defect. The result is more re-

alistic but the shape of the crack (which is randomly

chosen) does not seem enough realistic. This is why,

it appears important to propose a set of real images

with manual segmentations that are enough reliable to

be considered as reference segmentations or ”ground

truth” segmentations. To resume, the two ﬁrst kinds

of images allow to propose an exact evaluation and

to well illustrate the behavior of the method in theo-

retical cases whereas the last kind of images allows

to validate the work on real images with a ”pseudo”

ground truth.

Synthetic

image

Ground truth

Real image +

simulated

defect

Ground truth

Real image manually segmented

Reference segmentation or pseudo ground truth

segmentation

Figure 4: Tested images.

4.2 Reference Segmentation

For real images, we brieﬂy explain how the manual

segmentation is validated. Four experts manually give

a segmentation of the images with the same tools and

in the same conditions. Then, the four segmentations

are merged, following these rules:

1. A pixel marked as a crack by more than two ex-

perts is considered as a crack pixel;

2. Every pixel marked as a crack and next to a pixel

kept by step 1 or 2 is also considered as a crack.

The second rule is iterative and stops when no pixel

is added. Then, the result is dilated with a structuring

element of size 3×3.

In this part, we distinguish two datasets of real im-

ages. First, we have work with 10 images, in order to

validate our manual segmentation and to determine

how to ﬁx the parameters of the proposed method.

This ﬁrst dataset is called initial dataset. The sec-

ond one contains 32 images to complete the evalua-

tion and we called it the complementary dataset.

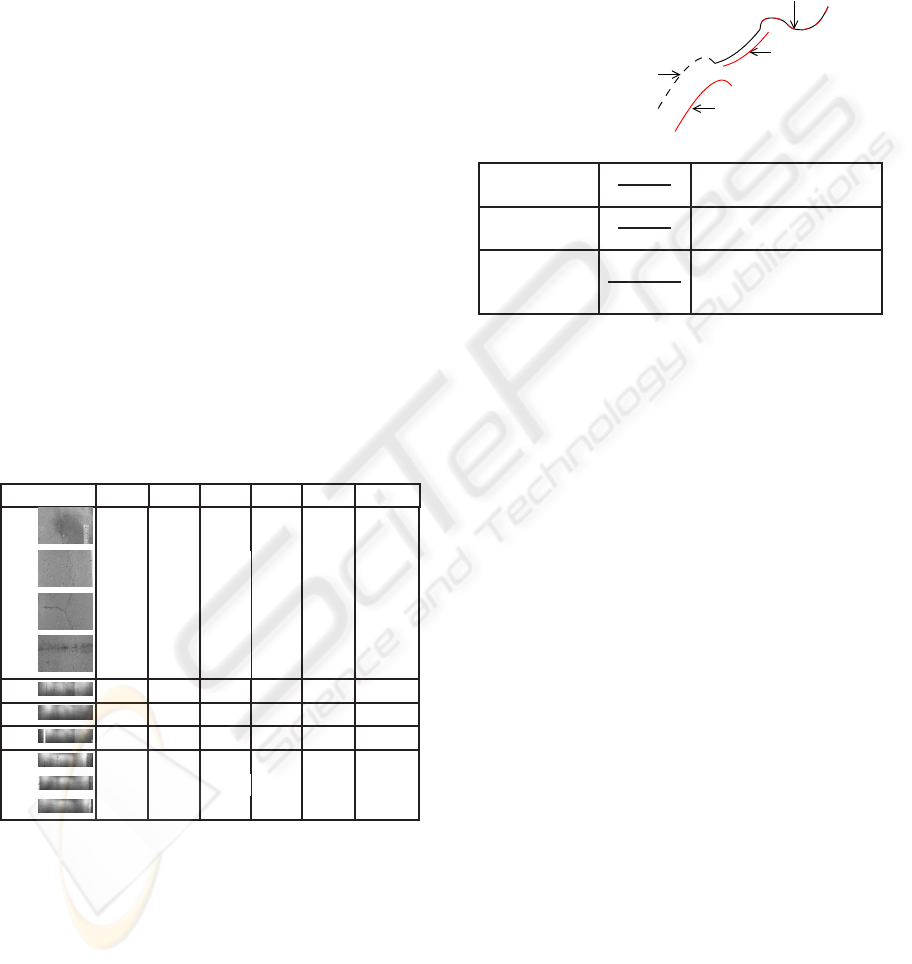
Initial Dataset. To evaluate the reliability of the ref-

erence segmentations, we estimate, ﬁrst, the percent-

age of covering between each operator, and, second,

the mean distance between each pixel (detected by

only one expert and not kept in the reference image)

and the reference segmentation. Table 3 compares the

results for these 10 ﬁrst images. We can notice that the

ﬁrst 4 images are the most reliable because the mean

error is less than 2 pixels. On the contrary, the last

6 images are less reliable but they are also the most

difﬁcult to extract a segmentation.

ROAD CRACK EXTRACTIONWITH ADAPTED FILTERING AND MARKOV MODEL-BASED SEGMENTATION -

Introduction and Validation

Complementary Dataset. The same technique is

used for establishing the reference segmentations

with 32 images. By analyzing the results for criteria

D., presented in Table 3, we decided to classify the 42

tested images in 3 categories:

1. Reliable: All the images have obtained D < 2 and

it means that all the operators have selected areas

that are quite close to each other and the segmen-

tation is reliable.

2. Quite reliable: All the images have obtained

2 ≤ D < 8, it means that some parts of the crack

are not easy to segment and there are locally big

errors.

3. Ambiguous: All the images have obtained D ≥8.

It clearly show that the images are really difﬁcult

to segment and in most of the cases, it means that

some parts are detected as a crack whereas they

are not a crack and reversely.

Table 3: Manual segmentation comparison for establishing

the reference segmentations – For each image, we give the

percentage of pixels that are preserved in the ﬁnal reference

segmentation compared to the size of the image (F), the per-

centage of covering between 2, 3 and 4 segmentations (over

all the pixels marked as crack by the 4 experts) and the sum

of them (S). For all the crack pixels not preserved in the

ﬁnal reference segmentation, the mean distance to this seg-

mentation is given, noted D.

Images F (%) 2 (%) 3 (%) 4 (%) S (%) D (pix)

37 0.45 28.87 9.79 1.59 40.25 1.48

42 0.4 26.69 14.59 4.2 45.48 1.45

46 0.72 27.53 11.66 2.33 41.52 1.41

40 0.44 34.3 19.01 5.87 59.18 1.03

463 0.17 23.46 5.95 0.39 29.8 1.4

936 0.41 23.52 7.41 0.9 31.83 7.05

41 0.33 22.64 7.31 1.33 31.28 3.56

23 0.6 24.12 9.41 2.45 36.58 2.23

352 1.01 25.69 11.52 2.15 39.36 4.75

88 1.44 22.74 8.23 1.23 32.2 2.76

4.3 Evaluation Criteria

In this section, we introduce how the reference seg-

mentation and the estimated segmentation are com-

pared. In Figure 5, we present common evaluation

criteria that are used for segmentation evaluation. We

have added the principle of ”accepted” detection that

tolerates a small error on the localization of crack

pixels. This criterion is needed because perfect de-

tection seems, for the moment, difﬁcult to reach, see

the results in Table 3, that illustrate this aspect. In

consequence, these ”accepted” pixels have been in-

cluded in the estimation of the similarity coefﬁcient

or DICE. The threshold for accepted pixels equals 0

for synthetic images whereas it depends on the mean

distances, see D. in table 3, for the real images.

True positives (TP)

Positives (P)

Accepted

False positives (FP)

False Negatives (FN)

True negatives (TN)

Sensitivity

TP+FN

Proportion of good

detections

Speciﬁcity

TN+FP

Proportion of

non-detected pixels

Similarity

coefﬁcient or

Dice similarity

2TP

FN+T P+P

Ratio between good

detections and

non-detections

Figure 5: Evaluation criteria – In this ﬁgure, it corresponds

to two simulated segmentations of the same crack: the black

one is manual (or the reference) and the red one is esti-

mated. The goal is to evaluate the quality of the estimated

segmentation, that corresponds to the Positives (P). All the

non-selected pixels that do not correspond to the crack are

called the True Negatives (TN). Piece of crack with the two

colors (red and black) are the correct detections or True Pos-

itives (TP). In the table, the criteria are resumed and in this

work, we have used the DICE because this coefﬁcient well

represents what we want to measure: the quality of the de-

tection against the percentage of the crack that is detected,

or, how to reduce false detections and to increase the den-

sity.

5 EXPERIMENTAL RESULTS

For the proposed method, we want to determine, ﬁrst,

how to ﬁx the different parameters, second, the pre-

processing steps that are necessary, and, ﬁnally, which

variant is the most efﬁcient. In consequence, we have

tested different:

• Parameter values – The weights α

, equation (7),

and α

, equation (9), are tested from 0 to 1 with a

step of 0.1.

• Pre-processings – These pre-processings have

been experimented to reduce noises induced by

texture, to increase the contrast of the defect and,

to reduce the light halo in some images (like the

last six ones presented in Table 3):

1. Threshold – Each pixel over a given threshold

is replaced by the local average gray levels.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

2. Smoothing – A 3×3 mean ﬁlter is applied.

3. Erosion – An erosion with a square structuring

element of size 3×3 is applied.

4. Restoration – It tries to combine the ad-

vantages of all the previous methods in three

steps: histogram equalization, thresholding

(like Threshold), and erosion (like Erosion).

• Algorithm variants – Four variants are compared:

1. Init – This is the initial method proposed

in (Subirats et al., 2006).

2. Gaus – This variant considers the crack as a

Gaussian function, see section 3.2.

3. InMM – This is the initial version with an im-

provement of the Markov model (new deﬁni-

tion of the sites and of the potential function),

see section 3.3.

4. GaMM – This is the Gaus version with the new

Markov model.

• Comparison – We have compared this method

with a method based on morphological tools and

that is quite similar to (Tanaka and Uematsu,

1998) noted Morph.

5.1 Parameter Inﬂuence

Among the results, two conclusions can be done. For

each variant and each pre-processing, the weights be-

tween the term for adapted ﬁltering and the term for

the Markovian modelling should be the same, see

equation (7), i.e. α

= 0.5. However, when more

weight is given to adapted ﬁltering , the quality of the

results is lower than when more weight is given to the

Markovian segmentation. It means that in this kind

of application, the geometric information is more re-

liable than the photometric one and it seems coherent

with the difﬁculties of the acquisition.

For the new Markov model, we have noticed that the

results are the best when the weights are the same be-

tween the orientation term and the distance term, see

equation (9), i.e. α

= 0.5. However, better results are

obtained when the weight of the orientation is greater

than the distance one instead of the reverse.

5.2 Pre-processing

These tests have been done with real images, be-

cause, a priori, synthetic images do not need pre-

processings. The results are given by:

Init Gaus InMM GaMM

Restoration Restoration Threshold Erosion

However, for the four ﬁrst images (acquired with

lighting conditions more comfortable than the light-

ing conditions of the next 6 ones), the pre-processing

is not signiﬁcant for increasing the quality of the re-

sults. Moreover, with the new Markov model, the pre-

processing step increases a little the quality.

Init

Gaus

InMM

GaMM

Similarity coefﬁcient

Synthetic images

GaMM

InMM

Gaus

Init

Similarity coefﬁcient

Real images

Figure 6: Variation of the similarity coefﬁcient, see ﬁg-

ure 5 – The ﬁrst graph shows the results for synthetic im-

ages (the 3 ﬁrst ones are obtained from real images with

simulated defect) and the second graph presents the results

with real images. Good performances of methods InMM

and GaMM can be noticed.

5.3 Variants

The results are separated in two cases: with synthetic

images and with real images. In Figure 6, the evolu-

tion of the similarity coefﬁcient, or DICE, for the 11

synthetic images and the 10 real images is presented.

With synthetic images, GaMM is clearly the best for

most of the images. However, for one image (the

ROAD CRACK EXTRACTIONWITH ADAPTED FILTERING AND MARKOV MODEL-BASED SEGMENTATION -

Introduction and Validation

GaMM

Morph

Similarity coefﬁcient

Real images

Mean

Figure 9: Comparison with Morph – The dotted lines illustrate the ﬁve different kinds of images tested. For the ﬁrst one (that

corresponds to real images with good illumination), the results are mixed whereas for the other ones, GaMM is the best.

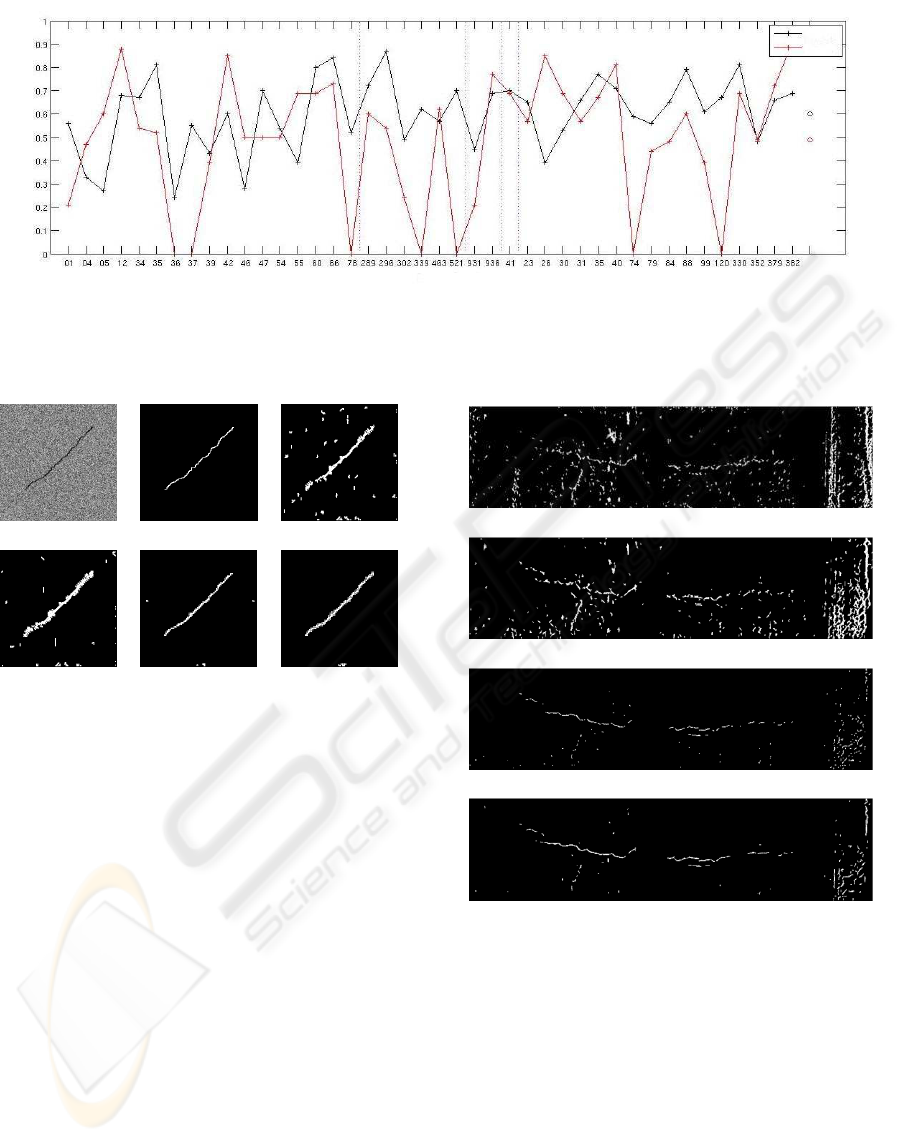
Image Ground truth Init

Gaus InMM GaMM

Figure 7: Segmentation results (synthetic images presented

in Figure 4) – These are the results obtained with the four

variants and it shows how GaMM gives the clearest result.

We can also notice the good result of InMM.

ﬁfth), the results are worse than with Gaus but they

are still correct (DICE=0.72). On the contrary, for the

most difﬁcult images (the 3 ﬁrst ones that contain a

real road background), GaMM obtains acceptable re-

sults (DICE > 0.5) whereas the other methods are not

efﬁcient at all. An illustration is given in Figure 7: it

shows how GaMM can reduce false detections.

The results with real images, see graph (b) in Fig-

ure 6, are coherent with those obtained with synthetic

images. The new Markov model allows the best im-

provements, compared to the initial method Init. The

method GaMM obtains the best results, except on few

images, see an example in ﬁgure 8, where InMM is

the best. However, GaMM gives results that are quite

similar and the differences are not signiﬁcant.

Init

Gaus

InMM

GaMM

Figure 8: Segmentation results (real images) – These are the

results obtained with the real images presented in ﬁgure 4.

Method InMM obtains the clearest detection (i.e. with less

false detection) but we can also noticed the good quality of

the detection map with GaMM.

5.4 Complementary Dataset and

Comparison

Finally, we have compared the result of GaMM on

each of the complementary dataset (32 images) with

the results obtained with a classic method based

on morphological tools, like (Tanaka and Uematsu,

1998). The mean DICE is 0.6 with GaMM whereas

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

it is 0.49 with the Morphology method, see Figure 9.

It shows how this new method outperforms this kind

of method. However, if we compare image per image,

the results show that in 50% of the cases GaMM is the

best, see illustrations of these results in Figures 10 and

11. More precisely, it seems more performant with

Ambiguous images, whereas the Morphology method

is the best with Reliable images, see § ”Complemen-

tary dataset”.

Synthetic image ”Ground truth”

segmentation

Morph FaMM

Real image Reference segmentation

Morph FaMM

Figure 10: Differences between Morph and GaMM – Ex-

amples with synthetic and real images. Morph outperforms

GaMM with simple synthetic images whereas GaMM gives

better detection with real images.

6 CONCLUSIONS

In a ﬁrst time, we have introduced new methods for

the detection of road cracks. In a second time, we

have presented a new evaluation and comparison pro-

tocol for automatic detection of road cracks and the

new methods are validated by this protocol. As far

as we are concerned, we proposed real images with

ground truth for the ﬁrst time in the community. Our

next work is to propose our ground truth to the com-

munity in order to havea larger comparison. Then, we

want to increase our data set by taking into account

Real image

Reference segmentation

Morph

GaMM

Figure 11: Differences between Morph and GaMM – Ex-

amples with real images acquired on a vehicule. The detec-

tion with GaMM is more complete than with Morph.

the different qualities of road surface or road tex-

ture (because for the moment, each proposed method

seems very dependent on the road texture). Finally,

we want to reﬁne our evaluation criteria by using (Ar-

belaez et al., 2009).

REFERENCES

Acosta, J., Adolfo, L., and Mullen, R. (1992). Low-cost

video image processing system for evaluating pave-

ment surface distress. TRR: Journal of the Transporta-

tion Research Board, 1348:63–72.

Arbelaez, P., Fowlkes, C., and Malik, J. (2009). From con-

tours to regions: An empirical evaluation. In Com-

puter Vision and Pattern Recognition. To appear.

Augereau, B., Tremblais, B., Khoudeir, M., and Legeay, V.

(2001). A differential approach for ﬁssures detection

on road surface images. In International Conference

on Quality Control by Artiﬁcial Vision.

Bray, J., Verma, B., Li, X., and He, W. (2006). A neural

nework based technique for automatic classiﬁcation

of road cracks. In International Joint Conference on

Neural Networks, pages 907–912.

Chambon, S., Subirats, P., and Dumoulin, J. (2009). Intro-

duction of a wavelet transform based on 2d matched

ﬁlter in a markov random ﬁeld for ﬁne structure ex-

traction: Application on road crack detection. In

IS&T/SPIE Electronic Imaging - Image Processing:

Machine Vision Applications II.

ROAD CRACK EXTRACTIONWITH ADAPTED FILTERING AND MARKOV MODEL-BASED SEGMENTATION -

Introduction and Validation

Cheng, H., Chen, J., Glazier, C., and Hu, Y. (1999). Novel

approach to pavement cracking detection based on

fuzzy set theory. Journal of Computing in Civil En-

gineering, 13(4):270–280.

Chou, J., O’Neill, W., and Cheng, H. (1995). Pavement

distress evaluation using fuzzy logic and moment in-

variants. TRR: Journal of the Transportation Research

Board, 1505:39–46.

Delagnes, P. and Barba, D. (1995). A markov random ﬁeld

for rectilinear structure extraction in pavement distress

image analysis. In International Conference on Image

Processing, volume 1, pages 446–449.

Elbehiery, H., Hefnawy, A., and Elewa, M. (2005). Sur-

face defects detection for ceramic tiles using image

processing and morphological techniques. Proceed-

ings of World Academy of Science, Engineering and

Technology (PWASET), 5:158–162.

Fukuhara, T., Terada, K., Nagao, M., Kasahara, A., and

Ichihashi, S. (1990). Automatic pavement-distress-

survey system. Journal of Transportation Engineer-

ing, 116(3):280–286.

Iyer, S. and Sinha, S. (2005). A robust approach for auto-

matic detection and segmentation of cracks in under-

ground pipeline images. Image and Vision Computing,

23(10):921–933.

Kaseko, M. and Ritchie, S. (1993). A neural network-based

methodology for pavement crack detection and clas-

siﬁcation. Transportation Research Part C: Emerging

Technologies information, 1(1):275–291.

Koutsopoulos, H. and Downey, A. (1993). Primitive-based

classiﬁcation of pavement cracking images. Journal

of Transportation Engineering, 119(3):402–418.

Lee, H. and Oshima, H. (1994). New Crack-Imaging Proce-

dure Using Spatial Autocorrelation Function. Journal

of Transportation Engineering, 120(2):206–228.

Petrou, M., Kittler, J., and Song, K. (1996). Automatic sur-

face crack detection on textured materials. Journal of

Materials Processing Technology, 56(1–4):158–167.

Ritchie, S., Kaseko, M., and Bavarian, B. (1991). Develop-

ment of an intelligent system for automated pavement

evaluation. TRR: Journal of the Transportation Re-

search Board, 1311:112–119.

Schmidt, B. (2003). Automated pavement cracking assess-

ment equipment – state of the art. Technical Report

320, Surface Characteristics Technical Committee of

the World Road Association (PIARC).

Song, K., Petrou, M., and Kittler, J. (1992). Wigner based

crack detection in textured images. In International

Conference on Image Processing and its Applications,

pages 315–318.

Subirats, P., Fabre, O., Dumoulin, J., Legeay, V., and Barba,

D. (2006). Automation of pavement surface crack de-

tection with a matched ﬁltering to deﬁne the mother

wavelet function used. In European Signal Process-

ing Conference, EUSIPCO.

Tanaka, N. and Uematsu, K. (1998). A crack detection

method in road surface images using morphology. In

Machine Vision Applications, pages 154–157.

Wang, K., Li, G., and Gong, W. (2007). Wavelet-based

pavement distress image edge detection with ” trous”

algorithm. In Transportation Research Record, An-

nual Meeting, volume 2024, pages 73–81.

Zhou, J., Huang, P., and Chiang, F. (2005). Wavelet-based

pavement distress classiﬁcation. TRR: Journal of the

Transportation Research Board, 1940:89–98.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications