SEED–GROWING HEART SEGMENTATION IN HUMAN

ANGIOGRAMS

Antonio Bravo, Jos´e Clemente

Grupo de Bioingenier´ıa, Decanato de Investigaci´on, Universidad Nacional Experimental del T´achira

San Crist´obal 5001, Venezuela

Rub´en Medina

Grupo de Ingenier´ıa Biom´edica, Facultad de Ingenier´ıa, Universidad de Los Andes, M´erida 5101, Venezuela

Keywords:

Segmentation, Unsupervised clustering, Mean shift, Cardiac images, Human heart, Left ventricle.

Abstract:

In this paper an image segmentation scheme that is based on combinations of a non–parametric technique

and a seed based clustering algorithm is reported. The method has been applied to clinical unsubtracted

angiograms of the human heart. The ﬁrst step of the method consists in applying a mean shift–based ﬁlter in

order to improve the left ventricle cavity information in angiographic images. Second, the initial seed is semi–

automatically generated from the aortic valve manual localization by a specialist. Third, each angiographic

image is segmented using a clustering algorithm that begins with the seed which is grown until image pixels

associated to the left ventricle cavity are clustered. A validation is performed by comparing the estimated

contours with respect to contours manually traced by a cardiologists. From this validation stage the maximum

of the average contour error considering six angiographic sequences (a total of 178 images) is 7.30 %.

1 INTRODUCTION

Image segmentation methods are a prerequisite to ef-

ﬁciently analyze the cardiac function from image data

acquired by X–Ray angiographic systems during car-

diac exams. Information about the size and shape

of heart cavities during the cardiac cycle could be

extracted. The use of traditional segmenting proce-

dures to cardiac images does not allow to obtain ac-

curate results due to the complexity and variability

of the anatomic shapes. Low contrast, noise, and

non–uniformityof regional intensities are some of the

problems associated with X–ray based cardiac imag-

ing modalities.

Left ventricle (LV) cavity plays a major role in the

heart dynamics since it pumps oxygenated blood to

the entire body. Left ventricle angiograms are ob-

tained from a medical imaging modality based on X–

rays, after the injection of a contrast medium in the

cavities of the heart aiming at enhancing the contrast

with respect to other tissues. Such examination en-

ables the assessment of morphology and function of

the heart. Ventriculographic image analysis requires

a precise description of ventricular shape in order to

quantify the parameters associated with the cardiovas-

cular function (Kennedy et al., 1970) (Rabit, 2000)

or alternatively for performing the visualization of

this anatomical structure (Medina et al., 2004). LV

volumes and ejection fraction (EF) are important in-

dexes for clinical assessments of heart function (Yan

et al., 1978). The accurate description of ventric-

ular function is important, since cardiovascular dis-

ease (CVD) accounts for one third of the deaths in the

world (WHO, 2002).

The general image segmentation problem involves

the division of a dataset into groups of similar ob-

jects. Thus, image segmentation consists in deter-

mining the regions containing pixels that have simi-

lar properties (Jain et al., 1999). There are many dif-

ferent methods for cardiac image segmentation based

on supervised learning methods (Suzuki et al., 2004;

Oost et al., 2006) or unsupervised learning (learning

without teacher) (Sui et al., 2001; Bravo and Med-

ina, 2008) . In general, these methods provided an

accurate representation of ventricular borders, how-

ever, they are not yet fully validated and accepted by

clinicians as a gold standard.

The goal of this research is the developping of

Bravo A., Clemente J. and Medina R. (2010).

SEED–GROWING HEART SEGMENTATION IN HUMAN ANGIOGRAMS.

In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 91-96

DOI: 10.5220/0002848900910096

 SciTePress

a left ventricle semi–automatic segmentation method

based on unsupervised clustering. The performance

of the proposed method is quantiﬁed by estimating the

difference between the contours obtained by the our

approach with respect to the contours traced by the

cardiologist. The segmentation error is quantiﬁed by

using a set of metrics that has been proposed and used

in the literature (Suzuki et al., 2004; Bravo and Med-

ina, 2008). The paper is organized as follows. First,

the complete process that performs the segmentation

of the LV is detailed. Then, experiments carried out

to validate the method are presented, and the results

obtained are discussed. Finally, future developments

are proposed.

2 METHOD

2.1 Dataset

Six mono-plane angiograms acquired at several in-

stants of the cardiac cycle are used to evaluate the

proposed unsupervised clustering method for left ven-

tricle cavity identiﬁcation. The sequences of ventricu-

lographic images are acquired with a Siemens X–Ray

angiographic system, considering one standard exam-

ination view (right anterior oblique–RAO 30

◦

), with

a ﬁeld of view (FOV) of 27 cm, a spacing between

pixels of 0.285 mm, a frame rate of 25 images/s and

a total acquisition time of 2 s. The spatial resolution

of the image is 512× 512, with a depth of 8 bits per

pixel.

2.2 Image Enhancement

Non–parametric methods have been widely used in

segmentation problems due to their robustness in sta-

tistical analysis. These methods estimate the data

underlying distributions (unknown density function)

without prior knowledge of the distributions struc-

tures (Fukunaga, 1990).

The mean shift procedure is a non–parametric

technique that does not depend on any geometric

model assumptions (Fukunaga and Hostetler, 1975).

This procedure has been used in image processing

tasks such as ﬁltering and clustering (Comaniciu and

Meer, 2002). The objective of the procedure is to esti-

mate the density gradient based on kernel density esti-

mation method (Parzen window technique). This den-

sity gradient is deﬁned as the direction from a sample

point towards the center of its cluster. The estimated

density gradient (

∇f(x)) is used to obtain an estima-

tion (

f(x)) of the unknown density function (f(x)).

The main goal of the estimation is to characterize the

modes of the data distribution. These modes are com-

puted by iteratively moving the data according to a

mean shift vector calculated using (1).

(x) =

c h

∇f

(x)

(1)

where h is the bandwidth (smoothing kernel parame-

ter) and c is the normalization constant.

According to (1) the mean shift vector in the point

x is aligned with the local gradient of the estimated

density function. The idea is to track the path leading

x to the stationary point of the estimated density. The

stationary points in the estimated density represent the

modes of the data distribution. If the density function

modes are considered cluster centers, the mean–shift

ﬁltering algorithm shrinks data points towards these

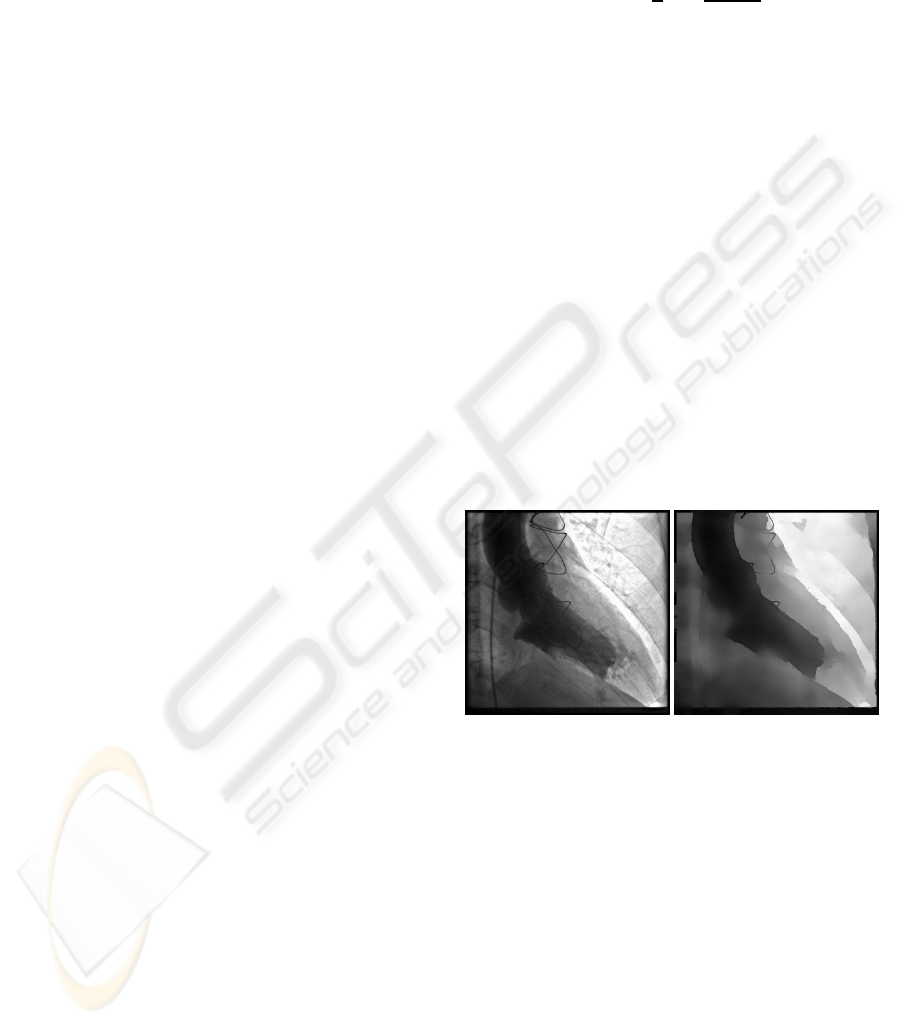
centers. A ﬁltering example is shown in Figure 1.

An end–systole ventriculogram image (RAO view) is

used to illustrate the preprocessing stage. This ven-

triculogram corresponds with the end–systole image

of the patient after a surgical ventricular restoration

(SVR) (Ferrazzi et al., 2006). In the ﬁltered image

(Figure 1.b) is shown that part of the patches of autol-

ogous or artiﬁcial material that are placed to close the

defect are removed. Additionally, the left ventricle

cavity information is enhanced.

(a) (b)

Figure 1: Enhancement process. (a) Original image. (b)

Mean shift ﬁltered image.

2.3 Segmentation Stage

A region growing technique is used to segment the

LV. Region growing methods have been used for per-

forming the segmentation of several medical imaging

modalities (Lehmann et al., 2005). The region grow-

ing is usually based on simple linkage, on multiple

connections or centroid based linkage (Haralick and

Shapiro, 1992).

The unsupervised clustering algorithm proposed

in this paper requires a seed point located inside the

region of interest to identify the cardiac cavity. The

seed is established in one angiographic projection

(one time instant of the image sequence).

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

2.3.1 Seed Selection Procedure

The seed is used for starting the region–growing seg-

mentation process. This seed is established in the 2–D

image I

(t represents the time instant of the angiog-

raphy dataset) according to following procedure:

1. A manual process performed by a cardiologist is

applied to locate the aortic valve sides (VA and

VP).

2. After the aortic valve points are identiﬁed, they

are joined starting from the VA point and ending

in the VP point using a straight line. The distance

l between VA and VP points is computed.

3. The midpoint (V

) of the line described by VA

and VP points is computed. This midpoint is used

to construct a new line perpendicular to the line

described by VA and VP points.

4. The seed point is the one located at the distance

l measured along the perpendicular line from the

point. This procedure must guarantee that y

coordinate of the seed point is greater than y coor-

dinate of the V

point.

Figure 2 shows the seed selection procedure. A

silhouette of the left ventricle contour is used to illus-

trate the selection procedure.

Figure 2: Seed point selection.

When the image I

has been segmented (process

described in section 2.3.2) a binary image

is ob-

tained. In this image, pixels in white represent the

segmented region. From

the seed points neces-

sary to segment the entire angiographic sequence are

estimated. The center of mass of the segmented re-

gion in the image

is calculated and denoted as

r(x, y). The pixel r(x, y) is the new seed to segment

the image I

t+1

The procedure based on calculation of the center

of mass, results in a point located very near of the

LV anatomical axis. In consequence, the seed point

is always located inside the target region (inside the

LV).

2.3.2 Region Growing Algorithm

The algorithm is developed using dynamic linked–

lists. The algorithm inputs are the enhanced image

and a binary image with all pixels set to zero (0). The

lists are implemented as a First In First Out (FIFO)

queue. The list is used to store temporarily the pix-

els that fulﬁll the clustering criterion. The objective is

to develop an iterative algorithm highly efﬁcient with

respect to memory requirements aiming at avoiding

memory overﬂows. Each node in the list contains the

pixel information: location and gray level intensity.

The ﬁrst node inserted in the list is the seed pixel. An

overview of the proposed algorithm is shown on the

ﬂowchart in Figure 3. After introducing the seed in

the FIFO list, the algorithm considers the following

steps:

1. The ﬁrst node of the list is dequeue.

2. The gray level information associated with the an-

alyzed node is compared with pixel intensities in a

8 pixels neighborhood to determine if these neigh-

bor pixels belong or not to the target region. The

pixels of the neighborhood that fulﬁll the cluster-

ing criterion are inserted at the end of the list and

their values in the binary image are modiﬁed to

one (1). The pixels that do not fulﬁll the condi-

tion are rejected.

3. The algorithm continues with this process while

there are nodes in the list. The algorithm output

is the binary image where pixels values set to one

represent the region of interest.

The uniformity criterion for grouping the pixels is

as follows: pixels are grouped if the difference be-

tween the pixel value in the neighborhood and the in-

tensity of the pixel extracted from the list is below

of the standard deviation of pixels in the enhanced

image.

2.3.3 Validation

In order to validate the proposed method, the differ-

ence between the estimated LV shape with respect to

a ground truth shape, traced by an expert is quanti-

ﬁed. A methodology to evaluate the LV segmenta-

tion method is considered. The approach proposed

by Suzuki et al. (Suzuki et al., 2004) for evaluating

the performance is incorporated. Suzuki’s quantita-

tive evaluation methodology is based on calculating

two metrics that represent the contour error (E

) and

the area error (E

). Equations (2) and (3) show the

contour and area errors expressions.

SEED-GROWING HEART SEGMENTATION IN HUMAN ANGIOGRAMS

Figure 3: Clustering process.

∑

x,y∈R

(x, y) ⊕ a

(x, y)]

∑

x,y∈R

(x, y)

, (2)

∑

x,y∈R

(x, y) −

∑

x,y∈R

(x, y)|

∑

x,y∈R

(x, y)

, (3)

where:

(x, y) =



1, (x, y) ∈ R

0, otherwise

, (4)

(x, y) =



1, (x, y) ∈ R

0, otherwise

, (5)

where R

is the region corresponding to the im-

age support, R

is the region enclosed by the con-

tour traced by the cardiologist, R

is the region en-

closed by the contour obtained by our segmentation

approach, and ⊕ is the exclusive OR operator.

3 RESULTS

Figure 4 shows the results of the segmentation for six

ventriculogramsequences. The contours traced by the

cardiologist are represented by white dashdotted lines

and the contours obtained with our approach are rep-

resented by black dashdotted lines. The ﬁrst and third

column show the end–systole images while the sec-

ond anf fourth column show the end–diastole images.

Tables 1–3 show a comparison of extracted con-

tours with respect to the contours traced by the car-

diologist. In these tables, the mean, the maximun

(max), the minimun (min) and the standard deviation

(std) for contour and area errors calculated according

to Suzuki’s metrics are shown.

Table 1 shows the errors for 178 images included

in all ventriculographic sequences.

Table 1: Errors obtained for a total of 178 images processed.

min mean max std

[%] 2.11 3.45 5.71 1.16

[%] 4.24 7.30 10.38 2.45

Tables 2 and 3 show the errors obtained for end–

diastole and end–systole images, respectively.

Table 2: Contour and area errors for end–diastole images.

min mean max std

[%] 2.91 4.07 5.23 1.64

[%] 4.99 6.86 8.72 2.63

The volume for the left ventricle during the car-

diac cycle is estimated using the Area-Length method

(Kennedy et al., 1970) from the contours obtained us-

ing the segmentation method. The correlation values

between the clinical parameters (end–diastole volume

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

Figure 4: Results of LV segmentation. Ground truth (white dashdotted line) and estimated contour (black dashdotted line).

Table 3: Contour and area errors for end–systole images.

min mean max std

[%] 2.19 3.37 4.16 1.07

[%] 4.24 6.58 9.03 2.40

and end–systole volume) estimated using the LV con-

tours obtained with the proposed method and those

estimated from contours traced by a cardiologist was

determined using the squared correlation coefﬁcient.

The correlation values were 0.9977 for end–diastole

volume and 0.9983 for end–systole volume.

4 DISCUSSION

The approaches recently reported were based on

quantifying only the errors at two cardiac instants:

end–diastole and end–systole. In this research, we

have estimated the segmentation error for all 152 im-

ages in the ventriculographic sequences. The aver-

age contour error obtained using our segmentation

method was 7.30 % which is smaller than the av-

erage error for the end–diastole contour (6.2%) and

end-systole contour (17.1%) reported by Suzuki et

al. (Suzuki et al., 2004). The average contour error

for the end–diastole (4.1%) reported using the semi–

automatic approach presented by Oost et al. (Oost

et al., 2006) is smaller than our value while the error

at end-systole (12.8%) is greater. However, the av-

erage area error (3.45%) obtained by our method is

smaller than the area errors reported in (Suzuki et al.,

2004; Oost et al., 2006).

A strong correlation between the clinical param-

eters (end–diastole volume and end–systole volume)

estimated using the left ventricle contours obtained

with proposed method and those estimated with the

contours traced by cardiologist was determined using

the squared correlation coefﬁcient.

Although our approach has been tested with a

smaller number of sequences of images than the ap-

proaches recently reported, we have considered ven-

triculograms with complex pathologies.

SEED-GROWING HEART SEGMENTATION IN HUMAN ANGIOGRAMS

5 CONCLUSIONS

A method for LV image segmentation from an-

giographics sequences was proposed. The pre–

processing stage was based on a mean shift procedure

aimed at performing the smoothing and enhancement

of image contours. A region growing algorithm was

controlled by a seed point located in an image at one

time instant, which was propagated to the rest of in-

stants in order to segment the entire angiographic se-

quence. The comparison was performed based on the

methodology proposed in (Suzuki et al., 2004) which

is also used in (Oost et al., 2006) and (Bravo and Med-

ina, 2008). The validation stage shows that errors are

small. The method allowed to detect LV important

features such as the papillary muscles.

As a future work, a more complete validation is

necessary, including a comparison of estimated pa-

rameters describing the cardiac function with respect

to results obtained using MSCT image modality.

ACKNOWLEDGEMENTS

The authors would like to thank the Investigation

Dean’s Ofﬁce of Universidad Nacional Experimen-

tal del T´achira and LOCTI grant PR0100401 for their

support to this project.

REFERENCES

Bravo, A. and Medina, R. (2008). An unsupervised clus-

tering framework for automatic segmentation of left

ventricle cavity in human heart angiograms. Comput

Med Imaging Graph., 32(5):396–408.

Comaniciu, D. and Meer, P. (2002). Mean shift: A robust

approach toward feature space analysis. IEEE Trans.

Pattern Anal. Machine Intell., 24(5):603–619.

Ferrazzi, P., Matteucci, M., Merlo, M., Iacovoni, A.,

Rescigno, G., Bottai, M., Parrella, P., Lorini, L.,

Senni, M., and Gavazzi, A. (2006). Surgical ven-

tricular reverse remodeling in severe ischemic dilated

cardiomyopathy: the relevance of the left ventricular

equator as a prognostic factor. J Throac Cardiovasc

Surg, 131(2):357–363.

Fukunaga, K. (1990). Introduction to Statistical Pattern

Recognition. Academic Press Inc, USA.

Fukunaga, K. and Hostetler, L. (1975). The estimation of

the gradient of a density function, with applications

in pattern recognition. IEEE Trans. Inform. Theory,

21(1):32–40.

Haralick, R. and Shapiro, L. (1992). Computer and Robot

Vision, volume I. Addison-Wesley Publishing Com-

pany, USA.

Jain, A., Murty, M., and Flynn, P. (1999). Data clustering:

a review. ACM Comp. Surv, 31(3):264–323.

Kennedy, J., Trenholme, S., Kaiser, I., and Wash, S. (1970).

Left ventricular volume and mass from single–plane

cineangiocardiogram. A comparison of anteroposte-

rior and right anterior oblique methods. Am Heart J,

80(3):343–352.

Lehmann, T. M., Beier, D., Thies, C., and Seidl, T.

(2005). Segmentation of medical images combining

local, regional, global, and hierarchical distances into

a bottom-up region merging scheme. In Proceedings

of SPIE, volume 5747, pages 546–555.

Medina, R., Garreau, M., Toro, J., Coatrieux, J. L., and

Jugo, D. (2004). Three–dimensional reconstruction

of left ventricle from two angiographic views: An ev-

idence combination approach. IEEE Transactions on

Systems, Man, and Cybernetics—Part A: Systems and

Humans, 34(3):359–370.

Oost, E., Koning, G., Sonka, M., Oemrawsingh, P. V.,

Reiber, J. H. C., and Lelieveldt, B. P. F. (2006). Auto-

mated contour detection in X–ray left ventricular an-

giograms using multiview active appearance models

and dynamic programming. IEEE Trans. Med. Imag.,

25(9):1158–1171.

Rabit, O. (2000). Quantitative analysis of cardiac function.

In Bankman, I. N., editor, Handbook of Medical Imag-

ing: Processing and Analysis, pages 359–374. Aca-

demic Press, San Diego.

Sui, L., Haralick, R., and Sheehan, F. (2001). A knowledge–

based boundary delineation system for contrast ven-

triculograms. IEEE Trans. Inform. Technol. Biomed.,

5(2):116–132.

Suzuki, K., Horiba, I., Sugie, N., and Nanki, M. (2004). Ex-

traction of left ventricular contours from left ventricu-

lograms by means of a neural edge detector. IEEE

Trans. Med. Imag., 23(3):330–339.

WHO (2002). Reducing risk and promoting healthy life.

The World Health Report 2002 Geneva, World Health

Organization.

Yan, S., Lamberto, B., Vladir, M., and Harry, G. (1978).

From Cardiac Catheterization Data to hemodynamic

Parameters. F. A. Davis Company, USA.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications