A NONLINEAR VERTEX-BASED MODEL FOR ANIMATION OF

TWO-DIMENSIONAL DRY FOAM

Micky Kelager and Kenny Erleben

eScience Center, Department of Computer Science, University of Copenhagen, Denmark

Keywords:

Dry foam dynamics, Vertex-based model, Nonlinear equations, Nonlinear and nonsmooth systems.

Abstract:

Foam is the natural phenomenon of bubbles that arise due to nucleation of gas in liquids. The current state

of art in Computer Graphics rarely includes foam effects on large scales. In this paper we introduce a vertex-

based, quasi-static equilibrium model from the ﬁeld of Computational Physics as a new paradigm for foam

effects. Dynamic processes like gas diffusion and bubble collapse are added prior equilibration. Animation-

wise the numerical model is well behaved and stable and can converge even if the foam is locally ill-deﬁned.

A novel contribution is the Ghost-Bubble method that allows foam simulations with free dynamic boundary

conditions. The presented model is interesting and well suited for 2D graphics applications like video games

and procedural or animated textures.

1 FOAM ANIMATION IN

COMPUTER GRAPHICS

Many methods to simulate liquid ﬂuids have been pre-

sented in Computer Graphics (Stam, 1999; Losasso

et al., 2004; Selle et al., 2005; Losasso et al., 2006)

with a common focus on realism. We believe that

the next step in ﬂuids dynamics lies within the sub-

ject of liquid foams, or froths. The scientiﬁc work

on foam dynamics in Computer Graphics is sparse.

In our opinion the most promising result to animate

beer froth still has issues with the motion and be-

havior of the foam (Cleary et al., 2007) but the still

frames from the foam simulations seem very convinc-

ing. We argue that the foam animation problems in

Computer Graphics are caused by the fact that foams

are treated as ﬂuids and not as real foams. We be-

lieve that the theoretic foundation of foam dynamics

must be obtained from Computational Physics. In this

paper we revisit a vertex-based foam model from the

ﬁeld of Computational Physics and derive a mathe-

matical model with a discretization that is suitable for

the purpose of Computer Graphics.

Our focus is directed towards two-dimensional

foams. This dimensional restriction is due to that

physics literature commonly only agrees on the pro-

cesses of two-dimensional foams and how they are

behaving whereas three-dimensional foams are not

yet completely understood. Two-dimensional foams

also exist in the real three-dimensional world, e.g. a

liquid foam constrained between two glass plates or

the single layer of foam resting on a surface. Addi-

tionally, in this paper we only focus on the behav-

ior of dry foams as wet foams are not as accurate

described by current physical models (Weaire et al.,

2003). We handle the dynamics and internal forces

of the dry foam along with external interactive contri-

butions, e.g. topological changes, gas diffusion, and

bubble collapses, but omit external dynamic forces

and collision handling. However, the method is based

on a Lagrangian representation and as such additional

external couplings and interactions can be handled at

vertex level.

This paper introduces the Ghost-Bubble method

which is a novel contribution for the two-dimensional

vertex-based foam model. The Ghost-Bubble method

allows dry foam simulations with free dynamic sur-

faces and ﬁnite boundaries. We derive a nonlinear

Newton method for the dry foam model and our dis-

crete model can converge even if the foam is lo-

cally ill-deﬁned. The model has less than 1% to-

tal error even though we use ﬁrst order ﬁnite differ-

ence approximations. The presented physics-based

dry foam model is interesting and well suited for two-

dimensional graphics applications like video games

and procedural or animated textures.

296

Kelager M. and Erleben K. (2010).

A NONLINEAR VERTEX-BASED MODEL FOR ANIMATION OF TWO-DIMENSIONAL DRY FOAM.

In Proceedings of the International Conference on Computer Graphics Theory and Applications, pages 296-303

DOI: 10.5220/0002849002960303

 SciTePress

2 PREVIOUS WORK

Computer Graphics has a greater interest in how bub-

bles and foam simulations are visualized while Com-

putational Physics is more keen on trying to under-

stand, describe, and measure all the different physics

processes within a foam.

Analytic and iterative relaxation-based geometri-

cal methods have been used in Computer Graphics to

render foam and bubbles. For instance in (Icart and

Arqu

es, 1999) empirical laws were used to construct

a bubble-bubble interaction model to describe a single

layer of foam bubbles. Constructive solid geometry

(CSG) and analytical solutions were used in (Glass-

ner, 2000a; Glassner, 2000b) to visualize small-sized

bubble clusters of 2-3 bubbles.

Lagrangian elastic models have also been at-

tempted. One such attempt employs an explicit

curvature-driven model where bubble-bubble interac-

tions are modeled using energy potential functions to

penalize unwanted bubble conﬁgurations (Durikovic,

2001). In this work gas diffusions and Plateau bor-

ders are ignored and the computational mesh is ﬁxed.

The shown foams consist of no more than 10 bub-

bles. In (Li and Volkov, 2006) a 2D elastic model is

extended with a pressure force model where pressure

variation in the external media is included to model

buoyancy. In (Iwasaki et al., 2004) a mass-spring sys-

tem is employed in a curvature-driven method similar

to (Durikovic, 2001). Results include visualizations

of 1-2 bubbles. The main contribution in this work is

a real-time rendering method that takes light interfer-

ence into account.

Fluid-based methods are another paradigm.

In (Hong and Kim, 2003) the volume-of-ﬂuid method

and the front-tracking method are combined. Inter-

faces are directly adjusted to avoid numerical diffu-

sion and yield mass conservation. This work ad-

dresses bubbles rising in a liquid but does not deal

with foams. A continuous multiphase ﬂuid simulator

is used in (Zheng et al., 2006) where a novel regional

level set method and a semi-implicit surface tension

model are introduced. Bubble thickness is explicit

modeled by a distribution function and the effect of

drainage is included. Gas diffusion is still not mod-

eled nor is it clear how to deal with boundary condi-

tions in the velocity ﬁeld. Results show 5-10 bubbles.

Lastly bubble-bubble interaction models have also

been addressed. (K

uck et al., 2002) models bubbles

using a mass-less spherical particle system. Springs

are added to model the bubble interactions. Bubble

creation and ﬁlm rupture are handled by adding and

removing bubbles randomly. Plateau borders are not

modeled but instead special ray-tracing shaders are

used to mimic the real foam structure. Results are

shown with 700-3000 bubbles. A virtual beer was

poured into a glass in (Cleary et al., 2007) using a La-

grangian model of smoothed particle hydrodynamics

(SPH) which makes the interaction between the multi-

phase ﬂuid very convincing. Gas diffusion is handled

and bubble collapsing is dealt with similar to (K

uck

et al., 2002). The foam model omits modeling the

foam ﬁlms and hence the importance of topological

changes. Rheology and shearing of the bubbles are

handled in a pseudo-physical way by including ex-

plicit cohesive forces between the particles. The mo-

tion of the dry foam on top of the beer is too rigid and

some realism is lost in this account.

In summary the work of foams done in Computer

Graphics are concerned with modeling ﬁlm thickness

such that the interference patterns can be shown dur-

ing rendering. However, many of the dynamic foam

processes are ignored, such as gas diffusion, foam

rupture, and topological changes. Our method in-

cludes all of these. Lately, the work on bubbles and

foams in Computer Graphics have begun integrating

physically ideas (Cleary et al., 2007; Kim et al., 2007)

which allow foams and bubble clusters to behave

more convincingly. Common for the two-dimensional

foam models in Computational Physics are the re-

quirement of inﬁnite networks which imply periodic

boundary conditions in the numerical simulations.

Distribution functions and statistics are natural inter-

ests within Computational Physics where dynamical

effects come secondary (Weaire and Kermode, 1983;

Kawasaki et al., 1989; Bolton and Weaire, 1992).

Our work introduces the vertex-based foam model

to the ﬁeld of Computer Graphics. The model in-

cludes effects not previously presented in Computer

Graphics. Further we extend the model to deal with

free moving foam boundaries. We demonstrate exam-

ples of dry foam networks up to 10.000 bubbles. As

far as we know this is an order of magnitude larger

than previous published results on 2D foam simula-

tions in Computer Graphics.

3 A PRIMER ON PHYSICS OF 2D

DRY FOAM

We now brieﬂy review the basics of 2D dry foam. A

complete source of theory can be found in (Weaire

and Hutzler, 1999). A foam is a two-phase system

in which bubbles of gas are enclosed by thin layers

of a liquid substance. Regularly a foam is disordered

which refers to the bubbles within the foam that can

vary greatly in size. Ordered foams usually do not oc-

cur in real life and are therefore a topic of theoretical

A NONLINEAR VERTEX-BASED MODEL FOR ANIMATION OF TWO-DIMENSIONAL DRY FOAM

297

research. Liquid foam has a form that is categorized

as cellular due to that bubbles of gas form cells that

are surrounded by liquid. In a two-dimensional foam

the Plateau borders coincide with the foam ﬁlms.

Thus, a foam can be structured into three elements;

bubbles/cells, ﬁlms/Plateau borders, and Plateau junc-

tions. In terms of mesh topology these elements cor-

respond to faces, edges, and vertices, respectively.

This apparently complex two-phase material has a

well-deﬁned local structure which allows progress in

predicting the dynamic properties of the foam. The

different types of foams are generally categorized into

either liquid or solid. A liquid foam is a soft, highly

deformable, substance that range from wet to dry de-

pendent on how much of its volume that contains liq-

uid. A special variant of liquid foam is froth. We con-

centrate on liquid foams with the same characteristics

as soap foam.

A bubble will not shrink and decrease its sur-

face area to zero due to surface tension γ is balanced

against the pressure difference ∆p. This relation is

known as the law of Laplace-Young which is given

∆p = γ





2γ

, (1)

where R

and R

are the principal radii of curvature

for the surface with ∆p = (p

− p

) as the difference

between two adjacent cells i and j. In two dimensions

where r is the local radius of curvature

of a foam ﬁlm.

Plateau added a set of additional rules to the law of

Laplace-Young. These rules are vital for foam equi-

librium. For a two-dimensional dry foam the law of

Plateau states: The ﬁlms can intersect only three at a

time and must do so with an angle of φ = 120

◦

During equilibration and evolution of a dry foam

the network will undergo different structural changes.

These changes can be categorized into topological

processes entitled T1 and T2. It has been observed

that other topological restructurings in a foam are

combinations of one or more T1 and T2 processes.

In the two-dimensional T1 process the topological

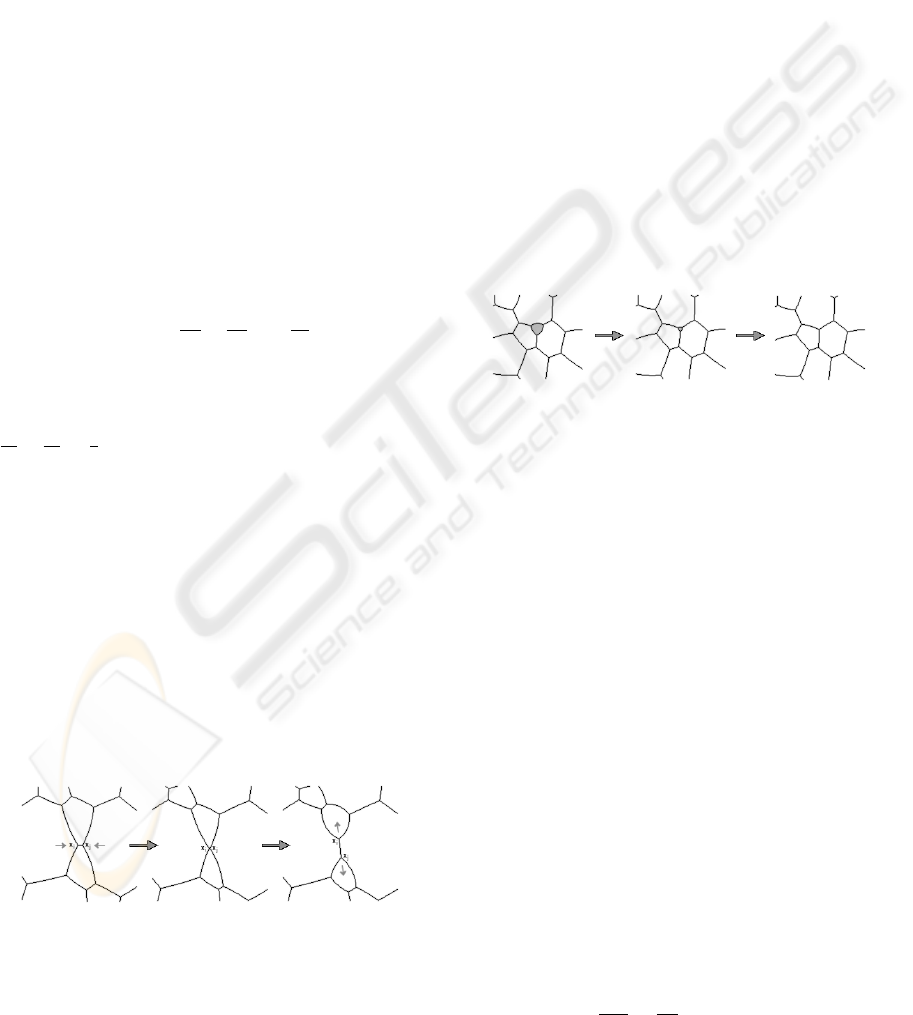
Figure 1: The T1 process on a 2D dry foam. An approach-

ing unstable four-fold vertex will be split into two stable

three-fold vertices.

change consists of exchanging, or ﬂipping, the ﬁlms

in question as depicted in Figure 1. When two three-

fold vertices are moving towards each other the dis-

tance between the vertices becomes zero and the foam

structure will be in an unstable conﬁguration. If the

distance between the vertices becomes close to zero,

or less than some threshold T

dist

, then a T1 process

takes place,

d ·

d < T

dist

∧ T

dist

> 0, (2)

where

d = (~x

−~x

) is the displacement vector be-

tween the two three-fold vertices. Generally, the

length of the ﬁlm is larger than k

d k as the ﬁlm is

curved due to the law of Laplace-Young. We will ar-

gue that the difference in lengths can be neglected as

dist

can be set sufﬁciently close to zero.

When the T1 condition (2) is satisﬁed the ﬂipping

strategy we choose is to place the ﬁlm vertices per-

pendicular to the line segment described by

d. If we

assume that the two vertices meet Plateau’s 120

◦

-rule

then due to the geometrical properties of the T1 oper-

ation the vertices will be forced to move apart.

Figure 2: The T2 process for a 2D dry foam. When a three-

sided cell approaches zero area due to gas diffusion it will

perish.

The T2 topological change consists of removing a

three-sided cell, as depicted in Figure 2, and occurs

due to gas diffusion. In a T2 process a foam cell will

collapse into a single vertex. The position of the re-

sulting vertex is set to the average of the three cell

vertices. The T2 process is performed when the cell

area is less or equal to some area threshold T

area

= 3 ∧ A

≤ T

area

∧ T

area

≥ 0, (3)

where n

designates the number of sides of the i

cell

and A

is the current area of the cell. Cells with more

than three sides can also collapse. Here a number of

T1 operations ﬂip the smaller ﬁlms in the cell until a

three-sided cell is formed.

Gas diffusion is driven by the pressure differences

between adjacent cells across their common bound-

aries. Some cells will grow at the expense of others

but in the end all cells will perish. This evolution of

a foam is called coarsening. By far the most com-

mon applied model for coarsening in an ideal two-

dimensional dry foam is known as von Neumann’s

law,

2π

γκ(n

− 6), (4)

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

298

where κ is a diffusion constant. This law shows that

cells with more than six sides steadily enlarge while

cells with less than six sides steadily decrease in area.

4 THE VERTEX-BASED DRY

FOAM MODEL

In this section we construct the mathematical equi-

librium model for a two-dimensional dry foam based

on the laws of foam physics. We assume that viscous

forces and inertial effects are negligible. The enclosed

gas is treated as incompressible such that the foam

will minimize the surface energy at all times (Weaire

and Kermode, 1983). For now we assume a foam with

periodic boundaries which implies that each vertex

has three ﬁlms and three adjacent cells. Let V , E , F

and A be index sets of vertices, edges, faces, and ver-

tex angles, respectively. The dry foam mesh consists

of faces that correspond to bubble cells. The f

cell is

labeled with its current area A

and pressure p

, while

junctions have positions where the v

vertex has co-

ordinates ~v





. We measure the angle of

intersection between two ﬁlms, i.e. edges, meeting at

a junction, and denote these vertex angles by φ

for

a ∈ A. From geometry and the law of Laplace-Young

it follows that the cell areas and angles of ﬁlm inter-

sections can be written as functions of vertex posi-

tions and cell pressures.

The rule of Plateau results in a constraint for each

vertex angle

2π

− φ

= 0 ∀a ∈ A. (5)

The cell areas may be controlled by a similar con-

straint

target

− A

= 0 ∀ f ∈ F . (6)

The target area A

target

is coupled with von Neumann’s

law to yield the equilibrium area during coarsening

of the dry foam. Next we agglomerate vertex coordi-

nates and cell pressures into one state vector

~x =

·· · ~v

kV k

·· · p

kF k

. (7)

The cell area and vertex angle constraints can similar

be agglomerated into a system of nonlinear equations

F(~x) =







target

− A

(~x)

target

kF k

− A

kF k

(~x)

2π

− φ

(~x)

2π

− φ

kAk

(~x)







0. (8)

A solution ~x

∗

for equilibrium must fulﬁll

F(~x

∗

) = 0.

Our idealized mathematical model may be summa-

rized into,

ideal model ⇔











von Neumann’s Law

Topological T1/T2 processes

State changes shear/collapse

F(~x) =

(9)

This model consists of a coupling of highly nonlinear

and non-smooth sub processes.

4.1 Discretization of the Mathematical

Model

As the ﬁrst step we apply a linearization to the whole

model. Essentially, this means that we solve the four

sub processes in an iterative manner until the system

converges. To determine the cell target areas for the

current iteration we apply an Euler discretization of

von Neumann’s Law. Secondly, we apply the topo-

logical processes and state changes as discrete events,

and ﬁnally we solve

F(~x) =

We apply a nonlinear Newton method for

F(~x) =

0 (Nocedal and Wright, 2006). Given the current it-

erate ~x

for some iteration k for which F(~x

) 6=

0, we

seek to ﬁnd ∆~x

such that F(~x

+ ∆~x

) =

0. Taking a

ﬁrst order Taylor series approximation gives

0 = F(~x

+ ∆~x

) ≈ F(~x

) +

dF(~x

)

d~x

∆~x

. (10)

Each iteration of the Newton method solves J

∆x

where J =

dF(~x

)

d~x

and

b = −F(~x

). The Newton up-

date ~x

k+1

= ~x

+ ∆~x

is done once a solution for the

step-direction

∆x

is found. There are many practi-

cal difﬁculties in a straightforward implementation.

An analytical solution to the Jacobian J is not feasi-

ble in practice due to the nonlinear implicit coupling

between the state variables. Further, non-singularity

for J is not guaranteed which implies that an inexact

Newton approach must be taken.

To remedy the problems above we apply a blocked

Gauss-Seidel approach to solve for the step-direction

and performing the Newton update. Blocks are cre-

ated from the state variables that are affected by the

vertices of the foam. A block corresponds to the x

and y coordinates of one vertex and the cell pressure

values p

, p

, and p

of the adjacent three cells that

are shared by the vertex. A similar approach is used

in (Kermode and Weaire, 1990). The Newton system

for a single block can now be written as

A NONLINEAR VERTEX-BASED MODEL FOR ANIMATION OF TWO-DIMENSIONAL DRY FOAM

299







∂A

∂p

∂A

∂p

∂A

∂p

∂A

∂x

∂A

∂y

∂A

∂p

∂A

∂p

∂A

∂p

∂A

∂x

∂A

∂y

∂A

∂p

∂A

∂p

∂A

∂p

∂A

∂x

∂A

∂y

∂φ

∂p

∂φ

∂p

∂φ

∂p

∂φ

∂x

∂φ

∂y

∂φ

∂p

∂φ

∂p

∂φ

∂p

∂φ

∂x

∂φ

∂y













∆p

∆x

∆y













∆A

∆φ







(11)

The right-hand side of (11) consists of the area and

angle constraints

∆A

= A

target

− A

f ∈ {i, j,k} ⊂ F , (12a)

∆φ

2π

− φ

a ∈ {i, j} ⊂ A. (12b)

The third angle φ

is not part of the Jacobian because

it is directly given by

= 2π − (φ

+ φ

). (13)

The partial derivatives of the blocked Jacobian ma-

trix are computed numerically by central difference

approximations. To ensure the central difference ap-

proximations are sufﬁciently accurate we apply a step

size-halving strategy until the absolute differences lie

within a given threshold. To avoid problems with pos-

sible singularities the resulting linear system is solved

using the method of Singular Value Decomposition

(SVD). The topological processes are dealt with di-

rectly in the foam mesh as they correspond to edge

ﬂips and face collapses. Von Neumann’s Law is dis-

cretized as

target

← A

target

2π

γκ(n

− 6), ∀ f ∈ F . (14)

Since we are dealing with a quasi-static simulation we

have chosen a time step size of unity.

4.2 The Ghost-Bubble Method

A foam with a freely movable surface can not have

periodic boundaries. A new dynamic boundary con-

dition must be applied to the vertex model to allow for

a free foam surface.

We introduce the Ghost-Bubble method which

adds one virtual bubble to the foam network. To make

the ghost bubble move with the foam itself we add it

on the back of the foam mesh. This is illustrated in

Figure 3. We seek to model the ghost bubble as a

natural element of the real world, i.e. a world bubble,

that deﬁnes the atmosphere that surrounds the foam.

When gas diffuses through boundary ﬁlms into the at-

mosphere the change in volume of the world is in-

signiﬁcant compared to the volume of the atmosphere.

(a) (b)

Figure 3: The ghost bubble. (a) The front of the foam mesh

deﬁnes the foam network. (b) The ghost bubble is deﬁned

on the back of the foam mesh where it reuses all existing

boundary vertices of the foam. It acts as a mirrored bubble

that contains all bubbles in the foam network.

From this argument the ghost bubble should retain a

constant area. The same argument holds for a con-

stant ghost bubble pressure. This results in the follow-

ing two rules; the ghost bubble must have constant,

inﬁnite area and constant, unit pressure.

A permutation of indices is performed prior set-

ting up (11) for a boundary block such that the ghost

bubble corresponds to the cell with index k. From our

rules we have ∆A

= ∆p

= 0 and the changes to the

Newton subsystem become,







∂A

∂p

∂A

∂p

∂A

∂x

∂A

∂y

∂A

∂p

∂A

∂p

∂A

∂x

∂A

∂y

0 0 0 0 0

∂φ

∂p

∂φ

∂p

∂φ

∂x

∂φ

∂y

∂φ

∂p

∂φ

∂p

∂φ

∂x

∂φ

∂y













∆p

∆x

∆y













∆A

∆φ







(15)

5 EXPERIMENTS AND RESULTS

We post-process Voronoi diagrams from random gen-

erated point sites to create initial networks for our

foam solver. This is similar to (Weaire and Kermode,

1984) and illustrated in Figure 4.

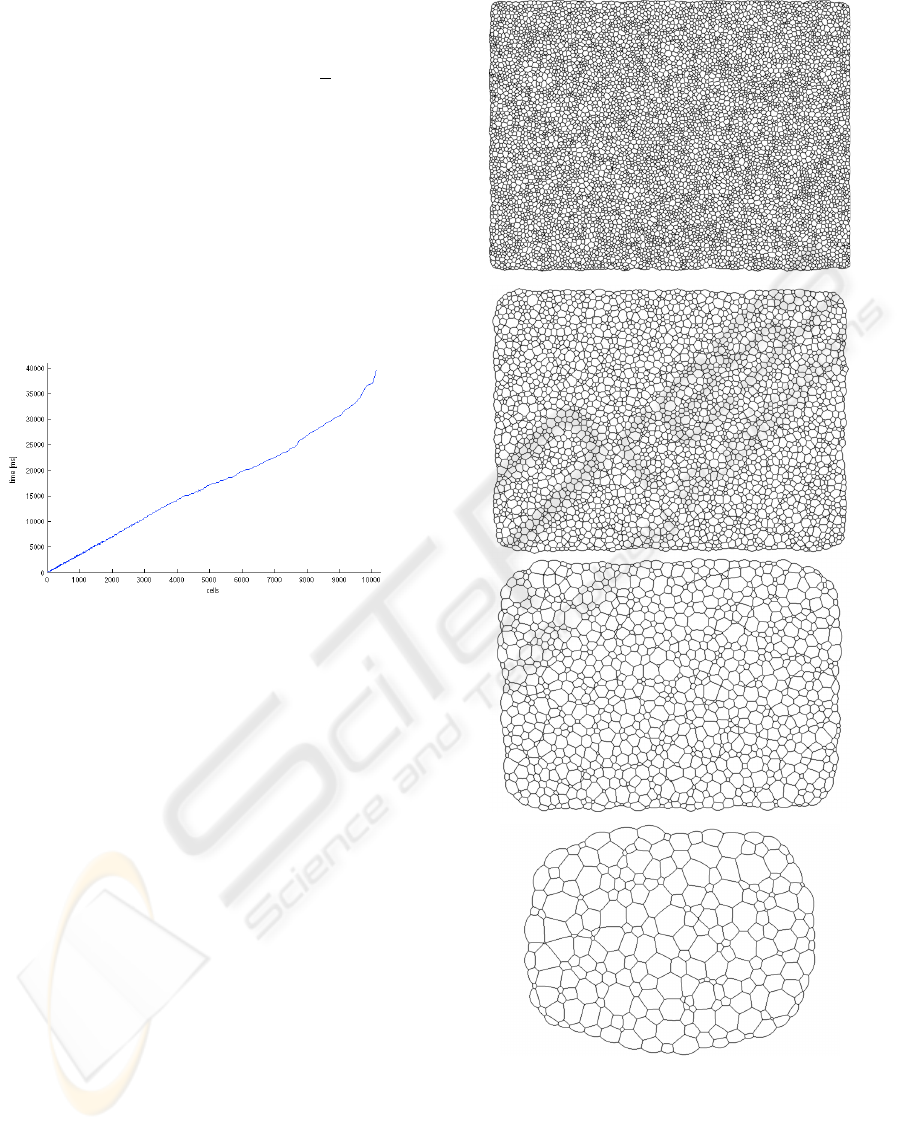
(a) (b)

Figure 4: In (a) a Voronoi diagram of 500 cells is gener-

ated from random point sites and (b) shows the correspond-

ing equilibrated 2D dry foam network with an area error of

0.001% and an angle error 0.01%.

Our experiments indicate that good threshold val-

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

300

ues for the topological conditions can be chosen as

0.01 ≤ {T

dist

area

} ≤ 0.25. (16)

We use the surface tension of γ ≈ 0.00025

. We have

evaluated the presented foam model by running hun-

dreds of simulations with different numbers of cells

and area sizes without any technical instabilities. We

have varied κ from [10

−3

..10

] and when a high value

of κ is employed the foam is collapsing more rapidly

similar to plain water foam.

We have measured the computation times from

different foam conﬁgurations and plotted them in

Figure 5. The plot depicts that the computation

time appears to scale linear in the number of cells.

Figures 4(b), 6, and 7 illustrate the free surface bound-

Figure 5: Time performance plot for a foam network evolv-

ing over time. The initial number of cells is 10k with a

frame time of 39.5s. The last frame contains 11 cells and

took 84ms. The simulation ran on a standard single core

2GHz laptop.

aries that is a result of the Ghost-Bubble method.

Figure 4 establishes that the dry foam model can

equilibrate a newly created foam. Four frames from

a complete foam evolution with initially 10, 000 cells

are shown in Figure 6.

To illustrate the foam bubble collapse mechanism

a random foam mesh of 66 cells have been used. The

dynamic gas diffusion process has been deactivated to

explicitly take control over which bubbles that should

disappear. T2 operations are forced upon the selected

bubbles. The result of a sequence of bubble collapses

is shown in Figure 7 where cells of 4, 5, and 6 edges

have been targeting for deletion.

The foam mesh can be rendered using ﬂat shaded

polygons. Figure 8 illustrates a large example of how

the pressure differences are distributed throughout a

foam. Notice that cells with similar pressures tend to

group together and form walls that almost makes the

image look like a labyrinth.

Figure 6: A foam is evolving with initially 10, 000 cells.

The time step is squared between each shown frame.

A NONLINEAR VERTEX-BASED MODEL FOR ANIMATION OF TWO-DIMENSIONAL DRY FOAM

301

(a) (b)

(e) (f)

Figure 7: Forced bubble collapse is performed on the dy-

namic foam boundary. Between each sub ﬁgure the marked

cell is next to be collapsed.

6 CONCLUSIONS AND FUTURE

WORK

We have introduced a new paradigm for foam simu-

lation from the ﬁeld of Computational Physics. Fur-

ther, we have presented a novel method to deal with

free moving boundaries in quasi-static simulation of

2D dry foam. Our discrete model has been developed

with focus on stability and robustness that are needed

in the ﬁeld of Computer Graphics. We believe that the

presented physics-based dry foam model is interest-

ing and well suited for 2D graphics applications like

video games and procedural or animated textures.

For future work we will add dynamic forces to

the foam model. From a performance point of view

we could replace the sequential blocked Gauss-Seidel

variant of the nonlinear Newton solver with a parallel

blocked red-black Gauss-Seidel variant. We may also

exploit that a dual mesh could encode the geometric

invariants of the rules of Plateau. This work may be

extended to 3D where tetrahedra would correspond to

ﬁlm junctions. However, it is not clear how to deal

with the topological processes in 3D, nor is it clear

how to reconstruct the curved surfaces of the ﬁlm ge-

ometry in 3D.

Figure 8: The cell pressures are visualized in ﬂat shaded

blue tones. The colors have been exaggerated to make the

difference more visible.

REFERENCES

Bolton, F. and Weaire, D. (1992). The effects of plateau

borders in the two-dimensional soap froth. II. gen-

eral simulation and analysis of rigidity loss transition.

Philosophical Magazine Part B, 65(3):473–487.

Cleary, P. W., Pyo, S. H., Prakash, M., and Koo, B. K.

(2007). Bubbling and frothing liquids. ACM Trans-

actions on Graphics, 26(3):97–1–97–6.

Durikovic, R. (2001). Animation of soap bubble dynam-

ics, cluster formation and collision. Comput. Graph.

Forum, 20(3).

Glassner, A. (2000a). Soap bubbles: Part 1. IEEE Comput.

Graph. Appl., 20(5):76–84.

Glassner, A. (2000b). Soap bubbles: Part 2. IEEE Comput.

Graph. Appl., 20(6):99–109.

Hong, J.-M. and Kim, C.-H. (2003). Animation of bubbles

in liquid. Comput. Graph. Forum, 22(3):253–262.

Icart, I. and Arqu

es, D. (1999). An approach to geometrical

and optical simulation of soap froth. Computers &

Graphics, 23(3):405–418.

Iwasaki, K., Matsuzawa, K., and Nishita, T. (2004). Real-

time rendering of soap bubbles taking into account

light interference. In CGI ’04: Proceedings of the

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

302

Computer Graphics International (CGI’04), pages

344–348, Washington, DC, USA. IEEE Computer So-

ciety.

Kawasaki, K., Nagai, T., and Nakashima, K. (1989). Vertex

models for two-dimensional grain growth. Philosoph-

ical Magazine Part B, 60(3):399–421.

Kermode, J. P. and Weaire, D. (1990). 2D-FROTH: a pro-

gram for the investigation of 2-dimensional froths.

Computer Physics Communications, 60(1):75–109.

Kim, B., Liu, Y., Llamas, I., Jiao, X., and Rossignac, J.

(2007). Simulation of bubbles in foam with the vol-

ume control method. In SIGGRAPH ’07: ACM SIG-

GRAPH 2007 papers, page 98, New York, NY, USA.

ACM.

uck, H., Vogelgsang, C., and Greiner, G. (2002). Simula-

tion and Rendering of Liquid Foams. In Proc. Graph-

ics Interface, pages 81–88.

Li, L. and Volkov, V. (2006). Inﬂatable models. J. Comput.

Sci. Technol., 21(2):154–158.

Losasso, F., Gibou, F., and Fedkiw, R. (2004). Simulating

water and smoke with an octree data structure. SIG-

GRAPH 2004, ACM TOG, 23:457–462.

Losasso, F., Shinar, T., Selle, A., and Fedkiw, R. (2006).

Multiple interacting liquids. SIGGRAPH 2006, ACM

TOG, 25:812–819.

Nocedal, J. and Wright, S. J. (2006). Numerical Optimiza-

tion. Springer, second edition.

Selle, A., Rasmussen, N., and Fedkiw, R. (2005). A vor-

tex particle method for smoke, water and explosions.

SIGGRAPH 2005, ACM TOG, 24:910–914.

Stam, J. (1999). Stable ﬂuids. In SIGGRAPH 1999 Confer-

ence Proceedings, pages 121–128.

Weaire, D. and Hutzler, S. (1999). The Physics of Foams.

Oxford University Press, New York.

Weaire, D., Hutzler, S., Cox, S., Kern, N., Alonso, M. D.,

and Drenckhan, W. (2003). The ﬂuid dynamics

of foams. Journal of Physics: Condensed Matter,

15(1):S65–S73.

Weaire, D. and Kermode, J. P. (1983). Computer simulation

of a two-dimensional soap froth - i. method and mo-

tivation. Philosophical Magazine Part B, 48(3):245–

259.

Weaire, D. and Kermode, J. P. (1984). Computer simula-

tion of a two-dimensional soap froth - ii. analysis of

results. Philosophical Magazine Part B, 50(3):379–

395.

Zheng, W., Yong, J.-H., and Paul, J.-C. (2006). Simu-

lation of bubbles. In SCA ’06: Proceedings of the

2006 ACM SIGGRAPH/Eurographics symposium on

Computer animation, pages 325–333, Aire-la-Ville,

Switzerland, Switzerland. Eurographics Association.

A NONLINEAR VERTEX-BASED MODEL FOR ANIMATION OF TWO-DIMENSIONAL DRY FOAM

303