MULTIPLE-CUE FACE TRACKING USING PARTICLE FILTER
EMBEDDED IN INCREMENTAL DISCRIMINANT MODELS
Zi-Yang Liu, Ju-Chin Chen and Jenn-Jier James Lien
Department of Computer Science and Information Engineering, National Cheng Kung University, Tainan, Taiwan
Keywords: Face Tracking, Multi-feature Particle Filter, Incremental LDA.
Abstract: This paper presents a multi-feature integrated algorithm incorporating a particle filter and the incremental
linear discriminant models for face tracking purposes. To solve the drift problem, the discriminant models
are constructed for colour and orientation feature to separate the face from the background clutter. The
colour and orientation features are described in the form of part-wisely concatenating histograms such that
the global information and local geometry can be preserved. Additionally, the proposed adaptive confidence
value for each feature is fused with the corresponding likelihood probability in a particle filter. To render
the face tracking system more robust toward variations in the facial appearance and background scene, the
LDA model for each feature is updated on a frame-by-frame basis by using the discriminant feature vectors
selected in accordance with a co-training approach. The experimental results show that the proposed system
deals successfully with face appearance variations (including out-of-plane rotations), partial occlusions,
varying illumination conditions, multiple scales and viewpoints, and cluttered background scenes.
1 INTRODUCTION
Visual tracking is an important requirement in many
machine vision applications, particularly those
associated with surveillance and human-computer
interaction. However, the implementation of
effective visual tracking schemes requires a number
of important issues to be resolved, including (1) the
need to detect the target object under varying
illumination conditions, degrees of occlusion, out-
of-plane rotations, and so on; (2) the need to
separate the target object from the background; and
(3) the need to predict the position of the target
object as it moves in a non-linear fashion.
Previous studies have shown that the separation
of an object from its background can be improved by
utilizing a multi-feature (multi-cue) method based
on the colour and orientation information within the
frame (Maggio et al., 2007; Moreno et al., 2008;
Tang et al., 2007). Multi-feature methods benefit
from a complementary characteristic. That is, when
one feature is unreliable as a result of occlusion or
heavy shadow, for example, the tracking system can
utilize other features of the image to accomplish the
separation or tracking function. However,
constructing a robust feature-based model capable of
representing the object of interest under all possible
appearance variations is a highly laborious and
challenging task. Accordingly, the literature contains
many proposals for updating the object
representation model on an on-line basis in order to
accommodate appearance variations. The most
notable proposals include the EigenTracking method
(Black et al., 1996), the condensation-conditional
density propagation scheme (Isard et al., 1998), and
the WSL tracker (Jepson et al., 2003).However, such
methods have only a limited success in updating the
object representation model since they neglect the
background information and therefore induce a drift
problem (Tang et al., 2007). Accordingly, more
recent studies (Avidan, 2007; Grabner, et al., 2006;
Moreno et al., 2008; Tang et al., 2007) have
attempted to achieve a more robust tracking
performance by incorporating the background
information into the updating process and treating
the tracking problem as a classification problem in
which the aim is to distinguish the pixels within the
target object region of the image from those within
the background region. The updated background
information obtained during the tracking process is
then used to update the classifiers utilizing either an
on-line boosting algorithm (Avidan, 2007; Grabner,
et al., 2006) or an on-line support vector machine
(SVM) method (Tang et al., 2007). However, despite
373
Liu Z., Chen J. and Lien J. (2010).
MULTIPLE-CUE FACE TRACKING USING PARTICLE FILTER EMBEDDED IN INCREMENTAL DISCRIMINANT MODELS.
In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 373-380
DOI: 10.5220/0002849803730380
Copyright
c
 SciTePress

the improved ability of the schemes in (Avidan,
2007; Grabner, et al., 2006; Moreno et al., 2008;
Tang et al., 2007) to update the classification models
on an on-line basis, the temporal information within
the image sequence is ignored.
To address the deficiencies of the various
schemes discussed above, this study proposes an
efficient integrated face tracking system in which the
colour and orientation feature information of the
target object (face) are processed in the particle
filter. As shown in Table 1, the proposed tracking
system consists of two modules: the initial tracking
process at the first frame (t=1) to construct the
discriminant models and the online process using
adaptive multi-feature particle filter to track the
target object in the following frames (t>1). In
particle filter, the observation probability of each
particle sample is calculated by combining the
likelihood probabilities provided by different
features (cues) with the corresponding feature
confidence values. Note that the feature confidence
values are automatically and adaptively assigned for
each feature with different background scenes in the
tracking process. In addition, linear discriminant
analysis (LDA) models are used for each feature to
separate the object from and background regions. To
render the face tracking system robust toward
variations in the face appearance and background
scene, the LDA models are updated on a frame-by-
frame basis using target object information selected
in accordance with a co-training approach.
2 INITIAL TRACKING PROCESS
The initial tracking process is shown in Table 1. The
proposed tracking system localizes the target object
in each frame
i with a rectangular window centred
at (u, v) with an orientation θ and a width and height
(w, h). Utilizing these parameters, the state of the
object at time t is defined as
(,,, , )xuvhw
tttttt
θ
=
(1)
The state of the object in the 1
st
frame,
1
x , is
obtained either via a manual labelling process or by
an existing detection algorithm such as Adaboost
(Viola et al., 2004).
Table 1: The multiple-cue face tracking system.
Input: Test video frames
{
}
T
III ,...,
21
Output: Estimated object state
{
}
t
x
x
x
,...,,
2
1
Initial Tracking Process (t=1):
1. Acquire object state x
1
in I
1
.
2. Obtain N
p
positive (face) particle samples
p
N
i
i
x
1
1
}{
=
and N
n
negative samples
n
N
i
i
x
1
1
}{
=
.
3. Crop the corresponding frame region for each
particle and obtain the colour and orientation
feature vector
i
t
c
and
i
t
g
, respectively.
4. Create colour-based LDA model Φ
t=1
and
orientation-based LDA model Ψ
t=1
On-line Tracking Process (t>1):
For t=2 to T
1. Generate particle samples
s
N
i
i
t
x
1
}{
=
and calculate
the likelihood probability
)|(
i
ttf
xzp
using the
corresponding LDA models Φ
t
and Ψ
t.
2. Estimate the adaptive confidence value:
color
t
λ
for colour feature using {
c
t
V
,
c
t
E
} and
norientatio
t
λ
for orientation feature using
{
o
t
V
,
o
t
E
} (Eq. (19))
3. Calculate the weight
i
t
w
for each particle (Eq.
(9)) and estimate the object state x
t
at current
frame (Eq. (6))
4. Update validation sets (Eqs. (13) and (14)) and
evaluation sets (Eqs. (15) and (16)).
5. Select new data sets
c
t
S
and
o
t
S
(Eqs.(20) and
(21))
6. Update LDA models: Φ
t+1
and Ψ
t+1
End
2.1 Colour and Orientation
Histogram-based Feature
Description
Each particle sample is represented using colour and
orientation information expressed in the form of a
histogram. To preserve the local information, the
sample is divided into semi-overlapped parts and
each part is represented by a colour and orientation
histogram, respectively. Then the colour feature
vector
i
t
c
and orientation feature vector
i
t
g
of the i
th
sample
i
t
x
at frame t are encoded by concatenating
part-wise histograms such that both global and local
target information and the spatial relations between
parts can be preserved in the concatenated histogram
(Maggio et al., 2007).
Having transferred the RGB image to the HSV
domain, the H channel is separated into N
H
bins and
the S channel into N
S
bins. The colour feature vector
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
374

of the sample
i
t
x
is then described by concatenating
all part-wise colour histograms as
{}
,
1
NN
rc
iu
i
cc
t
t
u
×
=
=
(2)
where u is total number of bins, the sample is
divided into N
r
parts and each part is represented by
one colour histogram with N
c
= N
H
+ N
S
bins.
For orientation feature, Sobel mask is applied to
each part of sample. The orientation range
[]
2/,2/
π
π
− is quantized into N
O
bins and the
magnitude of the gradient is accumulated on the bin
corresponding to its orientation. The orientation
feature vector of the sample
i
t
x
is described by
concatenating all part-wise orientation histograms as
{}
,
1
NN
r
iu
i
O
gg
t
t
u
×
=
=
(3)
Note that each part-wise orientation histogram is
normalized to one as well as each part-wise colour
histogram.
2.2 LDA Model Creation
In order to create the discriminant models to
separate the target object from background, Linear
Discriminant Analysis (LDA) (Lin et al., 2004;
Belhumeur et al., 1997) is applied in the proposed
tracker. To emulate possible variation of the target
object class, N
p
positive (face) samples
p
N
i
i
x
1
1
}{
=
are
generated by adding small Gaussian random noise to
the state
1
x and cropping the corresponding image
regions. On the contrary, with large Gaussian noise,
N
n
negative samples
n
N
i
i
x
1
1
}{
=
of background class are
generated. Note that each negative sample is treated
as a different class because of the diversity of the
background class, while all the positive samples are
assigned to a single class. As a result, a total of N
n
+1
classes exist for each feature. Thus, for each feature f
(i.e. colour or orientation feature), the between and
within scatter matrices f, i.e. S
B,f
and S
W,f
, can be
formulated as follows (Lin et al., 2004):
()()
,
NN
pn
T
SNC mmmm
n
Bf f f f f f
NN
pn
=+ − −
+
(4)
and
fpfW
CNS =
,
(5)
Where m
f
is the mean of feature calculated from the
feature vectors
p
N
i
i
t
f
1
}{
=
of samples
p
N
i
i
t
x
1
}{
=
; i.e.
i
t
i
t
cf =
for colour feature or
i
t
i
t
gf =
for orientation
feature; while
f
m and
f
C are mean and covariance
matrix calculated from the corresponding feature
vectors of the negative samples
n
N
i
i
t
x
1
}{
=
. Then the
projection matrix Φ and Ψ for colour-based and
orientation-based LDA models (spaces) can be
solved as the generalized eigenvalue problem with
corresponding between and within scatter matrices,
respectively.
3 ONLINE TRACKING
PROCESS USING ADAPTIVE
MULTI-FEATURE PARTICLE
FILTER
Particle filter has been applied in the online tracking
process, as shown in Table 1. We embed
incremental LDA models into particle filter
framework to form a robust tracking system. The
observation probability of a particle sample is
evaluating by fusing the likelihood probabilities of
both feature information with the corresponding
feature confidence values. At the end of each
incoming frame, the feature confidence values are
adaptively adjusted, while LDA models are
incrementally updated using the object information
selected in accordance with a co-training approach.
3.1 Likelihood Probability Fusion in
Particle Filter
The particle filter (Arulampalam et al., 2002) estimates
the object state
t
x
based on the previous to current
observations
t
z
:1
using a weighted sample set
s
N
i
i
t
i
tt
wxO
1
},{
=
=
, in which
∑
=
−==
s
N
i
i
tt
i
ttt
xxwOEZxp
1
:1
)(][)|( δ
(6)
where
i
t
w
is the weight associated with the sample
(particle)
i
t
x and
∑
=
=
s
N
i
i
t
w
1
1
.
i
t
w is defined by the
observation probability (likelihood) of observation
t
Z
at the state
i
t
x , as
)|(
i
tt
i
t
xzpw ∝
(7)
MULTIPLE-CUE FACE TRACKING USING PARTICLE FILTER EMBEDDED IN INCREMENTAL DISCRIMINANT
MODELS
375

In order to obtain samples
s
N
i
i
t
x
1
}{
=
, a drift step is
performed in which
{
}
s
N
i
i
t
i
tt
wxO
1
111
,
=
−−−
=
is re-sampled
according to the weight
s
N
i
i
t
w
1
1
}{
=
−
by Monte Carlo
method (Isard et al., 1998). Then, in a diffuse step
the re-sampled set
s
N
i
i
t
i
t
wx
1
}','{
=
is then propagated to
the new set
s
N
i
i
t
x
1
}{
=
in accordance with the state
transition model
)|(
1
i
tt
xxp
−
as
B
h
w
v
u
A
A
A
I
h
w
v
u
t
t
t
t
t
t
t
t
t
t
+
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
′
′
′
′
′
×
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
+=
⎥
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎢
⎣
⎡
−
−
−
−
−
1
1
1
1
1
3
2
1
00
0
0
00
00
00
000
000
θθ
(8)
where A
1,
and A
2
are two diagonal 2 by 2 matrices
and the element of matrices represents the different
ratio of object centres (u, v) and object size (w, v)
between consecutive frames, respectively; the A
3
represents the angle variation between frames and
vector B is a multivariate Gaussian random variable.
Finally, the estimation of the weight for each
sample (Eq. 7), the multi-feature algorithm proposed
in this study considers the likelihood probability of
both features. The overall likelihood probability
)|(
i
tt
xzp
for each sample can be thought of as a
mixture of the likelihood probabilities of each
feature with the corresponding feature confidence
value as
∑
∈
=
featuresf
i
ttf
f
t
i
tt
xzpxzp )|()|( λ
(9)
where
f
t
λ is defined as the confidence value of
feature f at time t,
f
t
λ =
color
t
λ
for colour feature and
norientatio
t
f
t
λλ =
for orientation feature, and
1=
∑
∈ featuref
f
t
λ
. Note that
norientatio
t
color
t
λλ =
is set to
0.5 for initialization.
For each sample
i
t
x
, the feature vectors of colour
and orientation information are projected via the
projection matrix Φ onto the colour-based LDA
space and Ψ onto the orientation-based LDA space,
respectively. The likelihood probability
)|(
i
ttf
xzp
is
weighted by a prior probability and defined as
),,,|()()|(
fff
i
tt
LDA
f
i
t
i
ttf
Ummxzpxpxzp
−+
=
(10)
where
)(
i
t
xp
is given i by
1
)(
−
−−
∝
t
i
t
xx
i
t
exp
(11)
The sample with larger difference of object
motion from the previous target object state x
t-1
is
given lower prior probability and the term
),,,|(
fff
i
tt
LDA
f
Ummxzp
−+
measured in each LDA
space, is defined as
)exp(),,,|(
f
tfft
T
ff
fff
i
tt
LDA
f
fUmfUm
Uxzp
σ
μμ
++−
−+
−−−
∝
(12)
where f
t
is the corresponding feature vector of
sample
i
t
x
(i.e.
i
t
c
or
i
t
g
) and
f
m
(
f
m
) is the
corresponding mean vector of the object
(background) class, U
f
is the project matrix (U
f
=Φ
for the colour-based LDA space while U
f
=Ψ for the
orientation-based ne),
f
T
ff
mUm =
+
and
f
T
ff
mUm =
−
represent the centres of object class and background
class in the LDA space, and
f
σ
is the noise
measurement for each feature, which is determined
experimentally based on that the orientation feature
is more affected by noise than colour feature
(Maggio et al., 2007).
3.2 Adaptive Confidence Value
Estimation
The idea for the estimation of the feature reliability
is motivated by Adaboost (
Freund, 1995) in which the
contribution of each weak classifier is weighting
according to its classification error. Similarly, at
each frame t, four data sets, two validation sets
c
t
V ,
o
t
V
and two evaluation sets
c
t
E
and
o
t
E
, are
collected for each feature in order to evaluate the
classification error that the samples from
background is classified as the target object class in
the LDA space. The validation sets are composed of
ground-truth feature vectors of samples belonging to
the target object (positive) and background
(negative) class, and
c
t
V contains the colour feature
vectors while
o
t
V contains the orientation ones. We
take the colour (or orientation) feature vector of the
object at the first frame, i.e.
1
c
(or
1
o
), as the
ground-truth positive data and include the feature
vectors belonging to the background classes at t-1
frame as the negative data to evaluate the feature
confidence value at time t,
{
}
2111111
)|()(| γγ ><∪=
−−−−
i
tt
LDA
f
i
t
i
t
c
t
xzpandxpccV
(13)
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
376

where
1
r
and
2
r
are the thresholds. Note that the
negative data consist of those feature vectors which
most generated from the background classes that
gives the lower prior probability (Eq. (11)) but
appears to be like the object class in the colour-
based LDA space. Similarity, the validation set for
orientation feature,
o
t
V , is defined as:
{
}
21
1
1111
)|()(| γγ ><∪=
−
−
−−
i
t
t
LDA
f
i
t
i
t
o
t
xzpandxpooV
(14)
where
1
o
is the orientation feature vector of the
object at the first frame and the feature vectors of
most likely background class are included.
The evaluation sets
c
t
E
and
o
t
E
are constructed
for colour and orientation feature at each frame
t,
respectively, as
⎭
⎬
⎫
⎩
⎨
⎧
>>=
43
)|()(| γγ
i
tt
LDA
f
i
t
t
i
c
t
xzpandxpcE
(15)
and
⎭
⎬
⎫
⎩
⎨
⎧
>>=
43
)|()(| γγ
i
tt
LDA
f
i
t
t
i
o
t
xzpandxpgE
(16)
where
3
r
and
4
r
are the thresholds and hence the
vectors in
c
t
E
and
o
t
E
contain the colour or
orientation feature vectors of samples from the
predicted object state at time
t. If most of the feature
vectors in evaluation sets are close to the
background class in the LDA space, this feature has
a lower confidence value and therefore plays a
diminished role in the prediction process.
Then the feature confidence value can be
measured in the LDA space via matrices Φ (or Ψ)
and the error of colour (or orientation) feature is
obtained by
∑
=
=
n
i
ii
ttf
f
xzp
1
)|( ηε
(17)
where
⎪
⎩
⎪
⎨
⎧
−Φ>−Φ
=
otherwise
fffif
f
i
t
Ti
t
T
i
,0
)()( ,1
1
μ
η
(18)
where index
f represents colour or orientation feature.
i
t
f
is the feature vector (as in Eq. (5)), f
1
is the
ground-truth feature vector (
f
1
= c
1
for colour feature
vector and
f
1
= g
1
for colour feature);
f
μ
is the mean
vector of the background classes in the
corresponding validation set
f
t
V
, and n is the number
of feature vectors in
f
t
E
. After measuring the error
for each feature, the confidence value
f
t
λ for each
feature
f is defined as
∑
∈
+
−=
featuresf
f
f
f
t
)(
1
τε
ε
λ
(19)
where
τ
is a small constant used to prevent a zero
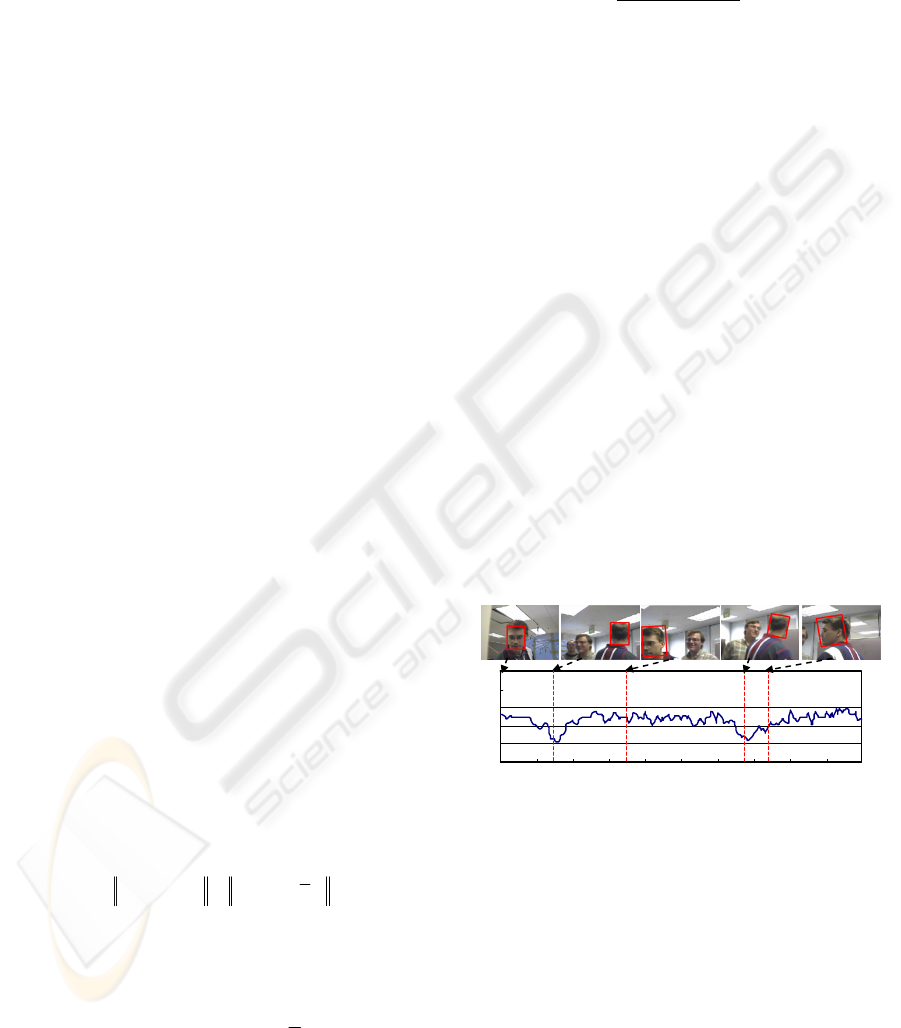
denominator. Fig. 1 shows an example of the
confidence value of colour feature in the tracking
process while the subject undergoes a 360° out-of-
plane rotation. Note that when the head turns, the
reliability of the colour feature decreases due to the
significant change from the initial colour
distribution.
3.3 LDA Model Updating
Having obtained the estimated object state, the LDA
model is updated in accordance with the target
object information in the current frame in order to
render the tracking system more robust to
appearance variations.
As shown in Table 1, at t
frame the updating process commences with the
updating of validation,
c
t
V
1+
and
o
t
V
1+
, and evaluation
sets,
c
t
E
1+
and
o
t
E
1+
, to the estimation feature
confidence value at the following frame t+1
accroding to Eqs. (13) and (15), and Eqs. (14) and
(16), respectively.
Figure 1: The evolution of the confidence value for colour
feature while the subject undergoes a 360° out-of-plane
rotation.
Before updating the LDA models, the co-training
approach (Tang et al., 2007) is applied to select the
discriminant feature vectors. The new data set
c
t
S
used for updating colour-based LDA model consists
of the discriminant colour feature vectors defined as
⎭
⎬
⎫
⎩
⎨
⎧
<∩>∩<=
== 221
)|()|()(| γγγ
i
tt
LDA
colf
i
tt
LDA
orif
i
t
i
t
c
t
xzpxzpxpcS
(20)
0
0.2
0.4
0.6
0.8
1
0 20 40 60 80 100 120 140 160 180
1
3 5236
Confidence Value
Frames
MULTIPLE-CUE FACE TRACKING USING PARTICLE FILTER EMBEDDED IN INCREMENTAL DISCRIMINANT
MODELS
377

where the first condition is based on the prior
probability to make sure the sample is mostly from
background class. The second and third conditions
pick out the samples which can’t be separated from
background class in the orientation-based LDA
space and thus the system need colour-based LDA
space to deal with these samples, i.e. to reduce the
likelihood value in the colour-based LDA space and
thus to reduce the overall likelihood probability for
rescuing from the confusion case. Similarly, the new
data set
o
t
S
used for updating orientation-based
LDA model can be defined as
⎭
⎬
⎫
⎩
⎨
⎧
>∩<∩<=
== 221
)|()|()(| γγγ
i
tt
LDA
colf
i
tt
LDA
orif
i
t
i
t
c
t
xzpxzpxpcS
(21)
Finally, for each feature type
f, the mean vectors
f
m
and
f
m
for the object and background classes
are updated by the SKL (sequential Karhunen-
Loeve) algorithm (Levy et al., 2000) using the new
data sets
c
t
S (or
o
t
S ) and the new LDA projection
matrix Φ (or Ψ) is then calculated using the
Incremental Fisher Linear Discriminant Model as in
(Lin et al., 2004).
4 EXPEREIMENTAL RESULTS
The effectiveness of the proposed tracking system
was evaluated using three different tracking
sequences, namely two noisy real-world video
sequence (H1, H2) captured from YouTube.com, a
head target sequences a (H3) taken from a
benchmark data set (
Birchfield, 1998). Table 2
summarizes the variation property of each test
sequence. The tracking system was initialized by
using
N
p
=150 object feature vectors and N
n
=400
background feature vectors to create LDA models Φ
and Ψ, respectively. In the tracking process, the
particle filter uses
N
s
=150 samples (Eq. (6)) and the
5-dimensional vector
B (Eq. (8)) is a multivariate
Gaussian random variable with zero mean and the
standard deviation of 10 pixels, 10 pixels, 8 pixels, 8
pixels, and 5 degrees, respectively. Note that the
thresholds used in building the validation sets and
evaluation sets were set experimentally a
s γ
1
=γ
3
=0.8,
γ
2
=γ
4
=0.7.
The accuracy of the tracking results obtained
from the AMF-PFI system was quantified using the
tracking error
)(te
, defined as the discrepancy
between the estimated target object state (estimated
target window) at time
t and the manually labelled
ground-truth state (ground-truth target window), i.e.
Table 2: Description of the test sequences.
Seq. Property
H1 Noisy, low-quality, real-world video
H2 Clutter, noisy, low-quality, real-world video
H3
Out-of-plane rotations, scale changes, clutter,
occlusions
)()(
)(2
1)(
tAtA
tO
te
eg
+
−=
(22)
where
∑
∈
−
+
−
=
TruePixelsyx
g
gi
g
gi
ii
h
vy
w
ux
tO
),(
22
)
2/
()
2/
()(
(23)
where
)(tO
sums the importance of the true positive
pixels utilizing distance as an importance measure.
),(
ii
yx is the x- and y- coordinate of the true
positive pixel,
w
g
, h
g
, (u
g
, v
g
) are the width, height,
and centre of the ground-truth target window,
respectively.
)(tA
g
and )(tA
e
are normalized
terms, which sums up the importance of all pixels
within the ground-truth and within the estimated
target, respectively.
The performance of the proposed system (names
as AMF-PFI) was compared with that of two other
systems, namely a system without adaptive feature
confidence value, denoted MF-PFI, and a system
without an incremental LDA model, denoted as
AMF-PF. Note that each test sequence was tested 10
times for each framework (Maggio et al., 2007).
Table 3 summarizes the mean and standard deviation
of the error metric for each of the three frameworks
when applied to the three test sequences. The results
confirm that the proposed system achieves a better
tracking performance than either the MF-PFI or
AMF-PF systems. The performance improvement is
particularly apparent for test sequences H1 and H2,
in which the targets exhibit significant appearance
changes over the course of the tracking sequence.
Fig. 2 shows the tracking results obtained by the
proposed system for test sequences H1 and H2. The
sequence H1 is simple case that the colour feature of
target object is much different from background but
in H2 the target object is cluttered by background. In
both sequences, the target object has out-of-plane
rotation. The results confirm the robustness of the
proposed system toward out-of-plane rotations. Fig.
3 shows the object tracking results (first row) for the
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
378

Table 3: Performance evaluation results (average mean and standard deviation of error metric) for MF-PFI, AMF-PI and
AMF-PFI systems for test sequences H1 to H3.
Error H1 H2 H3
MF-PFI: colour feature only
0.43±0.15 0.38±0.08 0.31±0.03
MF-PFI: orientation feature only
0.38±0.10 0.45±0.09 0.25±0.04
MF-PFI: fixed λ=0.5 for both features
0.39±0.09 0.38±0.05 0.25±0.02
AMF-PF: without incremental LDA model
0.44±0.07 0.43±0.03 0.23±0.02
AMF-PFI (the proposed system) 0.31±0.06 0.28±0.05 0.23±0.03

Figure 2: Representative results obtained using proposed system. First row: H1 sequence (frames 3, 7, 38, 51, and 60).
Second row: H2 sequence (frames 9, 18, 34, 61, and 97).
sequence H3. The tracking result as target object
class accompanied with new data sets
c
t
S and
o
t
S
(second and third row in Fig. 3), selected in each
frame as background class, are used for updating
LDA models. The results show that the system can
still track the target object (female) even partial
occlusions and would not cheated by another similar
object (male) even the object has similar skin colour
feature to the target object. Overall, the evaluation
results presented confirm the ability of the proposed
system to successfully track the target face and
facial appearance conditions.
5 CONCLUSIONS
This study has presented a multi-cue integrated
algorithm based on a particle filter for object (face)
tracking purpose. The proposed system incorporates
an incrementally updated LDA model for each
feature in order to render the tracking performance
more robust toward variations in the object
appearance or background scene, respectively. In
addition, the co-training approach is applied to select
discriminant feature vectors for LDA model
updating. Moreover, the likelihood probabilities
calculated from each feature are fused in the particle
filter with the corresponding feature confidence
value. Note that the feature confidence value is
adaptively updated on a frame-by-frame basis
according to different background scenes. The
experimental results have shown that the proposed
algorithm can successfully track objects
characterized by various out-of-plane rotations,
partial occlusions, scales or viewpoints, and
background scenes. In a future study, the algorithm
will be extended to the tracking of multiple objects
of the same class.
26
148
163
178
Figure 3: The first row shows the estimated object state at
time
t, which is added into the new data set as the target
object class. The second and third rows show the
corresponding new data (
c
t
S and
o
t
S ) selected as the
background class for updating the colour and orientation
LDA models, respectively.
REFERENCES
Arulampalam, M. S., Maskell, S., Gordon, N., and Clapp,
T. (2002). A tutorial on particle filters for online
nonlinear/non-gaussian Bayesian tracking.
IEEE
Transactions on Signal Processing
, 50(2): 174-188.
Avidan, S. (2007). Ensemble tracking.
IEEE Transactions
on Pattern Analysis Machine Intelligence
, 29(2): 261-
271.
MULTIPLE-CUE FACE TRACKING USING PARTICLE FILTER EMBEDDED IN INCREMENTAL DISCRIMINANT
MODELS
379

Belhumeur, P. N., Hespanha, J.P., and Kriegman, D.J.
(1997). Eigenfaces vs. Fisherfaces: Recognition using
class specific linear projection.
IEEE Transactions on
Pattern Analysis Machine Intelligence
, 19(7): 711-720.
Birchfield, S. (1998). Elliptical head tracking using
intensity gradients and color histograms. In
IEEE
Conference on Computer Vision and Pattern
Recognition.
Black, M. J., and Jepson, A. (1996). Eigentracking:
Robust matching and tracking of articulated objects
using a view-based representation. In
European
Conference on Computer Vision
.
Freund, Y. (1995). Boosting a weak learning algorithm by
majority.
Information and Computing. 121(2): 256-
285.
Grabner, H., Grabner, M., and Bischof, H. (2006). Real-
time tracking via on-line boosting. In
British Machine
Vision Association
.
Isard, M., and Blake, A. (1998). Condensation-conditional
density propagation for visual tracking.
International
Journal of Computer Vision
, 29(1): 5-28.
Jepson, A., Fleet, D., and El-Maraghi, T. (2003). Robust
online appearance models for visual tracking.
IEEE
Transactions on Pattern Analysis Machine
Intelligence, 25(10): 1296-1311.
Levy, A., and Lindenbaum, M. (2000). Sequential
karhunen-loeve basis extraction and its application to
image.
IEEE Transactions on Image Processing, 8(9):
1371–1374.
Lin, R.S., Yang, M.H., and Levinson, S.E. (2004). Object
tracking using incremental Fisher discriminant
analysis. In
IEEE Conference on Computer Vision and
Pattern Recognition
.
Maggio, E., Smerladi, F., and Cavallaro, A. (2007).
Adaptive multifeature tracking in a particle filtering
framework.
IEEE Transactions on Circuits and
Systems for Video Technology
. 17(10): 1348-1359.
Moreno-Noguer, F., Sanfeliu, A., and Samaras, D. (2008).
Dependent multiple cue integration for robust tracking.
IEEE Transactions on Pattern Analysis Machine
Intelligence, 30(4): 670-685.
Tang, F., Brennan, S., Zhao, Q., and Tao, H. (2007). Co-
tracking using semi-supervised support vector
machines, In
International Conference on Computer
Vision
.
Viola, P., and Jones, M. (2004). Robust real-time face
detection.
International Journal of Computer Vision,
57(2): 137-154.
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
380