EXPLICIT SOLUTION FOR THE MINIMUM DISTANCE

BETWEEN TWO SOLID SEMI-INFINITE CIRCULAR CONES

Baruch E. Karlin

Rafael, Aerodynamics Department, POBox 2250, Haifa, Israel

Keywords: Minimum Distance, Semi-infinite Cone, Geometric Reasoning, Explicit Solution.

Abstract: Multi-body kinematics and object rendering often involve minimum distance calculations. Explicit solutions

exist for the distance between spheres, cylinders and other simple objects. Deriving the minimum distance

between cones requires numerical minimization or geometrical approximations combined with analytical

solutions for the simpler objects. This paper describes an explicit solution for the minimum distance

between two solid semi-infinite circular cones. The method combines geometrical reasoning with analytical

derivation. The solution also includes the location of the intersection points. Solution regions are identified

and discussed. A numerical method based on minimizing the distance between two cone generators was

used as part of the verification process. The exact solution was compared to results of approximation by

regular polytopes. The explicit solution is robust, independent of coordinate system and invariant under

rigid translation and rotation of the setup.

1 INTRODUCTION

Multi-body kinematics and object rendering often

involve minimum distance calculations. Explicit

solutions exist for simple objects, including points,

lines, flat patches, spheres and cylinders. The

minimum distance between two circular cones can

be derived by numerical minimization or by

polyhedral approximation, combined with explicit

solutions for the simpler objects (The GJK

Algorithm: Gilbert 1988, Jovanoski 2008, Manchem

2009. Polytopes: Chung 1996).

The geometrical approximations have inherent

geometric inaccuracies and require iterative

refinements. Numerical procedures based on exact

parametric modeling require a good initial guess and

some number crunching. Nearly tangent cones

generators, steep slopes and discontinuities may

cause convergence difficulties. The computational

time of an iterative procedure may vary significantly

depending on the parameters of the problem.

This paper describes an explicit solution for the

minimum distance between two solid semi-infinite

circular cones. The method is based on geometrical

reasoning and vector algebra derivation. The

solution also includes the location of the intersection

points. Rendering and examples were implemented

with Matlab®.

2 METHOD

2.1 Scope

The cones dealt with in this paper are solid, circular,

semi-infinite, with positive generator angles smaller

than π/2. Axes referred to in this paper are the axes

of the cones. Each cone extends from apex to

infinity in the positive direction of its axis.

2.2 Nomenclature

a,b - cones’ axes

a,b - distances to intersection points on a and b

d - minimum distance vector between the cones

d - minimum distance between the cones

f,g - apex shift along a and b

p - minimum distance vector between axes

p - distance between cones' axes

r - extended minimum distance vector

r - length of extended minimum distance vector

α,β - generator angles of the cones

γ - positioning angle (between cones' axes)

crit

- critical positioning angle

ω - rotational positioning angle of polytope

2.3 Statement of the Problem

Given the positioning of two known cones, the pro-

154

E. Karlin B. (2010).

EXPLICIT SOLUTION FOR THE MINIMUM DISTANCE BETWEEN TWO SOLID SEMI-INFINITE CIRCULAR CONES.

In Proceedings of the International Conference on Computer Graphics Theory and Applications, pages 154-159

 SciTePress

blem is to find the minimum distance between their

surfaces (see Figure 1). The parameters of the

problem are the generator angles, the directions of

the axes, the distance between the axes, location of

the apexes, and the positioning angle (i.e., the angle

between the axes).

Figure 1: General view of two cones.

2.4 Geometric Setup

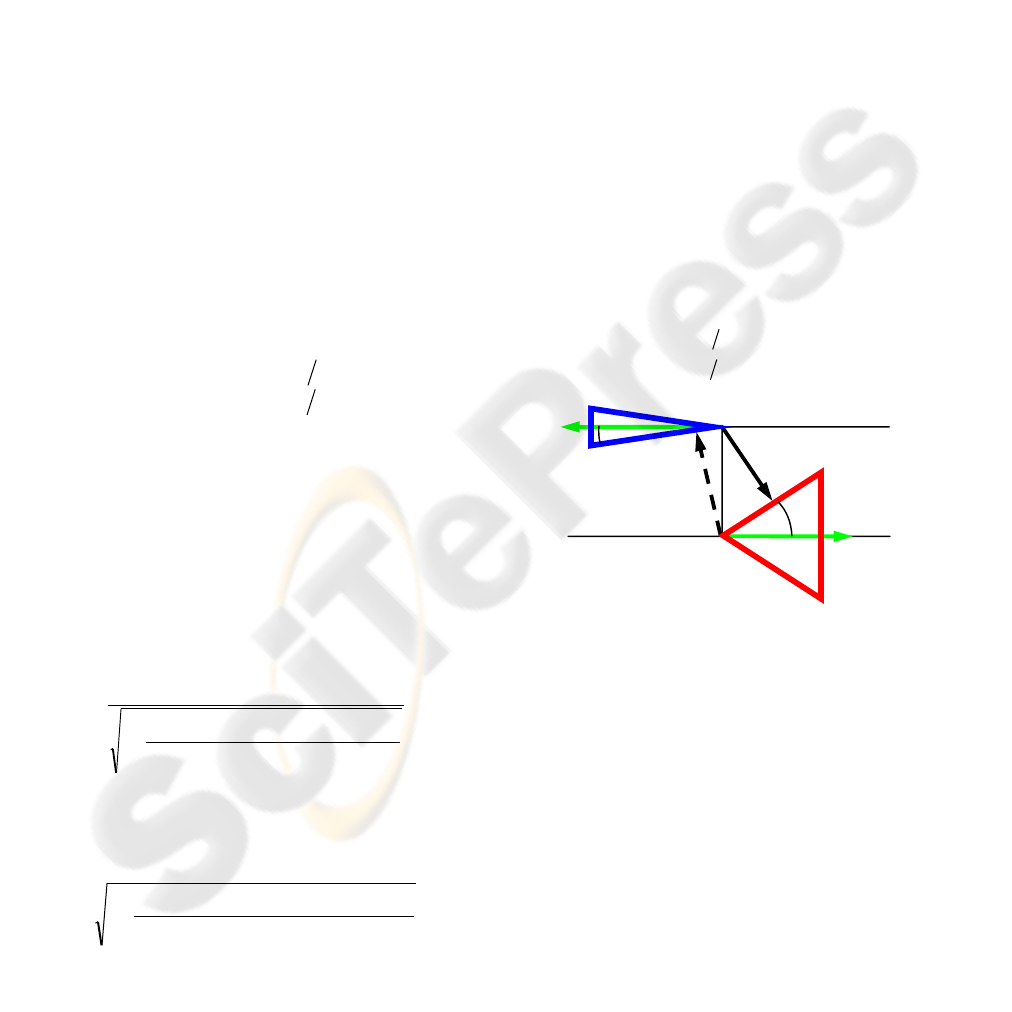
2.4.1 Non-Intersecting Axes

A-cone with axis a and generator angle α, and B-

cone with axis b and generator angle β are

positioned with angle γ and vector p between their

axes (see Figure 2). For symmetry reasons, the angle

between the axes is limited to [0, π].

Figure 2: Geometric setup – non-intersecting axes.

2.4.2 Intersecting Axes

For intersecting axes, the problem is planar. The

plane of reference contains the two axes. For each

cone, the geometric components of interest are the

axis, the apex, and the generator that lies in the

reference plane and is nearest to the other cone.

2.5 Geometric Reasoning

Geometric reasoning includes identifying the

different types of relative positioning, the geometric

characteristics of each type, and defining the

solution regions.

2.5.1 Geometric Types

There are three types of solutions: Surface-to-

Surface, Apex-to-Surface, and Apex-to-Apex. The

first two types have three regions: separation,

tangency and intersection. By definition, the third

type only has a separation region.

2.5.2 Surface to Surface

The minimum distance vector between the cones is

external and normal to both surfaces. The extended

vector intersects the A-axis at distance a from the

A-apex and the B-axis at distance b from the B-apex.

The normal to the cone is perpendicular to a specific

generator in the plane defined by the generator and

the axis (see Figure 2). The intersection point of the

extended vector with the axis is invariant in space

under translation of the cone along its axis.

2.5.3 Apex to Apex and Apex to Surface

For Apex-to-Surface, the minimum distance vector

between the cones originates at the apex of one cone

and is external and normal to the surface of the other

cone.

In the case of Apex-to-Apex, the minimum

distance vector between the cones is the vector

between the apexes.

2.5.4 Intersecting Axes

For a setup with intersecting axes, there are three

types of solutions: Apex-to-Generator, Apex-to-

Apex, and Parallel-Generators. There are also three

regions: separation, tangency and intersection.

Tangency includes coincident apexes, apex on

generator, and collinear generators.

2.6 Mathematical Formulation

2.6.1 Surface to Surface

The four vectors a, b, p, and r represented by their

unit counterparts satisfy the following relationship,

bpar

ˆˆˆ

bpar 

(1)

The dot product of the equation with each of the

Generator

Axis

Minimum

distance

Intersection

point

Axes

distance

Apex shift

Apex

EXPLICIT SOLUTION FOR THE MINIMUM DISTANCE BETWEEN TWO SOLID SEMI-INFINITE CIRCULAR

CONES

155

unit vectors gives a set of four equations,













rbrprarr

pbpppapr

bbbpbabr

abapaaar

ˆˆˆˆˆˆ

ˆˆˆ

ˆˆˆˆˆˆ

bpar

(2)

The distance vector r forms an angle of α-π/2

with the A-axis and of π/2-β with the B-axis. Vector

p is, by definition, perpendicular to the axes. So the

dot products of p, r, a and b are,















sin

ˆˆ

cos

ˆˆ

brar

babpap

(3)

By substituting these values into Equation 2 and

rearranging the terms, the intersection distances

satisfy the following set of linear equations,















sincos

rba

(4)

Solving the two equations gives the positions of

the intersection points on the axes as a function of

the angles and the distance between them,

 

















sinsincossin

sincossinsin

(5)

The distance between the intersection points

satisfies the quadratic equation,

 

 

sinsin

0sinsin

pbarr







:or

(6)

The intersection points on the axes are invariant

under apex shifts. Substituting a and b into the

equation gives the distance between the intersection

points,





sin

sincossinsin2sin







(7)

For zero apex shifts, the minimum distance d

(see Figure 2),







sin

sincossinsin2sin

sinsin







bard

(8)

For negative values of the discriminant in

Equation 8 the cones intersect (this is unconditional

intersection). The discriminant is zero for α+β=γ,

indicating tangency at infinity. For apex shifts of f

and g (see Figure 2), the minimum distance is,



sinsin

gfdd 

(9)

Substituting r from Equation 7 into Equation 5

gives the positioning of the extended minimum

distance vector.

2.6.2 Critical Positioning Angle

For semi-infinite cones, a and b are non-negative.

Then from Equation 5, since sin

γ and r are positive,

for zero apex shifts,









0sincossin



(10)

By geometric reasoning, for α<β the minimum

distance vector starts at the A-apex with a=0, and for

α>β the minimum distance vector ends at the B-apex

with b=0. By setting the two cases of Equation 10 to

zero, the critical value of the positioning angle for

either of the two cases is,

 

















for

crit

,sinsinarccos

(11)

Figure 3: Minimum for α>β and γ=π.

For values of the positioning angle between

critical value γ

crit

and π, the problem reduces to apex-

to-surface, and the minimum distance is constant

(see Figure 3),













forpbapd

forbpapd

tan,0,cos

0,tan,cos

(12)

For





(identical cones) and γ

crit

=π, the two

generators associated with the minima are parallel.

Any vector that is parallel to the minimum distance

vector between the two apexes (region marked in

yellow in Figure 4) is also a solution,



tan,cos pbapd 

(13)

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

156

Figure 4: Minimum for α=β and γ=π.

2.6.3 Apex Positioning

From Equation 9, any combination of shifts of the

cones along their axes that satisfies the equation

sinsin dgf 



brings the cones into

tangency. In particular, it happens with translation of

the A-cone by



sin

d

or translation of the

B-cone by



sin

d

along the appropriate axis.

Shifts beyond the point of tangency give a negative

minimum distance and cause intersection of the

cones. These are conditional tangency and

intersection (they depend on shift values).

For the special case α=β and γ=π (Equation 13),

the minimum reduces to a single line for a relative

apexes shift that is equal to p·tanα. For a larger shift,

the minimum distance is the distance between the

apexes. A relative shift of –p·cotα brings the cones

into tangency along segments of the two generators.

A larger shift in that direction causes intersection of

the cones.

2.6.4 Apex-to-Apex

In the Apex-to-Apex case, for each of the two cones,

define a cone with coinciding apex, axis in the

opposite direction, and generator angle of π/2-α or

π/2-β. These are the complementary cones. When

any of the cones is included entirely in the other

complementary cone, the minimum distance is the

distance between the apexes.

2.6.5 Identical Cones

When the two generator angles are equal,





, the

cones are identical. From Equation 8, the minimum

distance between the surfaces is then,

 

2sinsin1



d

(14)

This solution has three regions: (i) separation for

γ>2α; (ii) tangency of the surfaces at infinity for

γ=2α; (iii) intersection for γ<2α. Hence, regular

identical cones intersect when half the angle

between their axes is smaller than the generator

angle. Otherwise, there is a regular minimum

distance solution for cones with un-shifted apexes.

2.7 Intersecting Axes

2.7.1 Coincident Apexes

Coincident apexes are situated at the intersecting

point of the axes. In this case the distance between

the cones is zero.

2.7.2 Parallel Generators

Parallel generators occur when the angles satisfy

α+β=γ. The minimum distance is then the distance

between the two generators. Tangency occurs when

the distance is zero, and intersection occurs when it

is negative.

2.7.3 Apex-to-Generator

For the case of Apex-to-Generator, the minimum

distance is from the apex to the nearest point on the

inner generator of the other cone. The appropriate

combination (A-apex to B-cone or B-apex to A-cone)

is determined by the specific geometry.

Tangency occurs when an apex is situated on the

inner generator of the other cone. Intersection occurs

when an apex is situated between the two generators

of the other cone.

3 ANALYSIS AND EXAMPLES

3.1 Verification

Verification of solution and implementation was

carried out in part by comparing the explicit solution

with the results of numerical minimization based on

the distance between two cone generators: (a) Initial

guess: the generator nearest to the other cone in the

plane defined by the axis and the vector between the

axes; (b) Variables of the problem: the rotation angle

of the generator around the axis for each of the

cones; (c). The three types of regions have known

explicit solutions for the distance between two given

generators. They are are Ray-to-Ray, Point-to-Ray,

and Point-to-Point; (d). The cost function for the

minimization is the distance between the two

generators.

The algorithm was implemented in Matlab®

using a general minimization function without

EXPLICIT SOLUTION FOR THE MINIMUM DISTANCE BETWEEN TWO SOLID SEMI-INFINITE CIRCULAR

CONES

157

gradient. The process converged to the value of the

explicit solution within the required error bound (in

most of the region). It did, however, take longer by

four orders of magnitudes.

3.2 Comparison to Polytopes

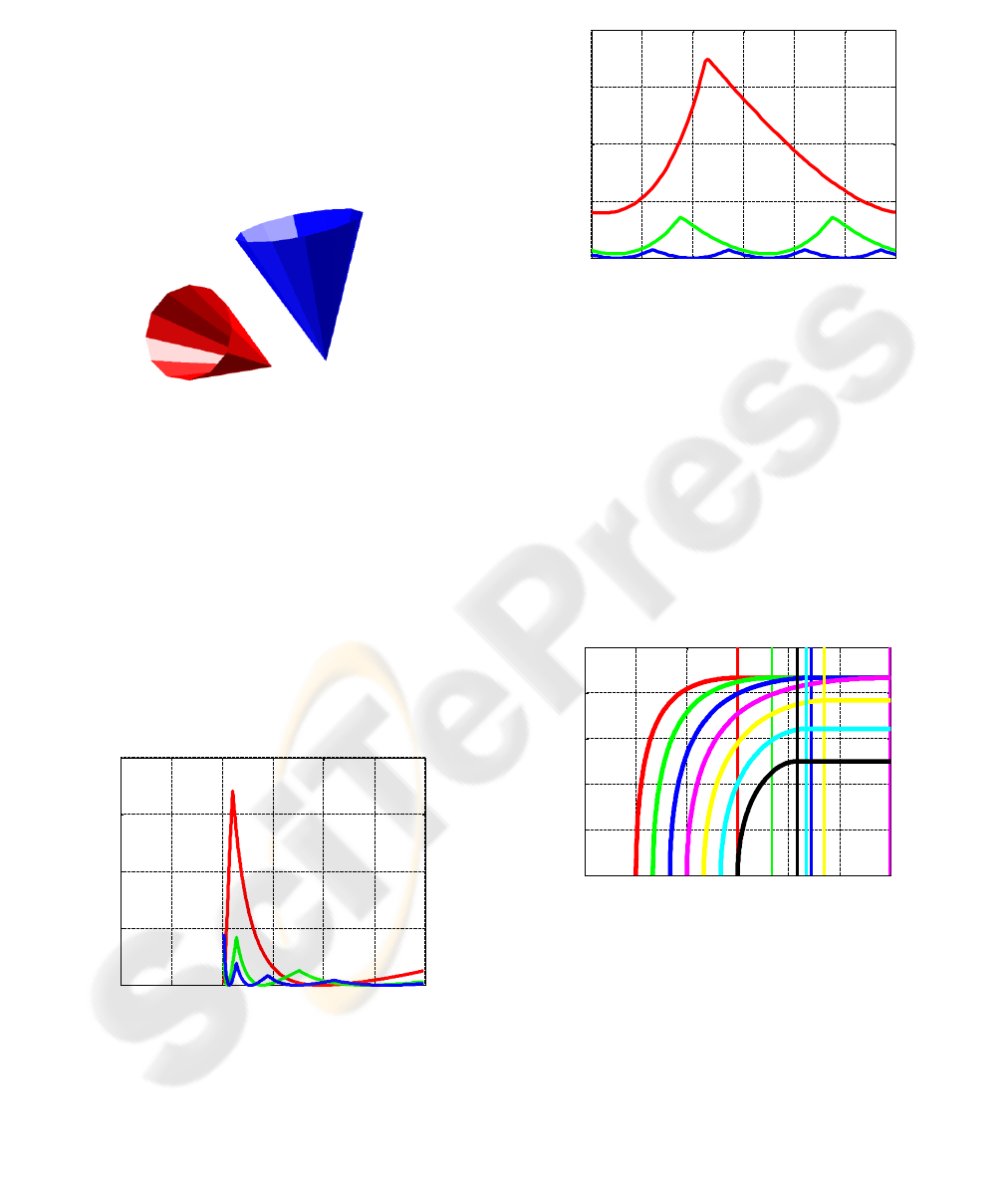
Cones can be approximated by circumscribed

regular polytopes (see Figure 5). For each polytope,

additional parameters of the problem are the number

of facets and the rotational positioning angle ω.

Figure 5: General view of two regular polytopes.

For non-intersecting axes, in the surface-to-

surface region the problem reduces to finding the

nearest pair of edges (one from each polytope). The

result is then compared to the explicit solution for

the cones. For simplification, the space metric was

scaled by the distance between the axes and the

apexes were set on the minimum vector between the

axes. The maximum possible distance for surface-to-

surface is then unity.

Figure 6 shows the approximation error versus

the axes positioning angle for various values of facet

numbers (color coded).

Figure 6: Approximation error vs axes angle.

Figure 7 shows the approximation error versus

the rotational positioning angle of the first polytope

for various values of facet numbers (color coded). In

both Figures 6 and 7, the rotation the second

polytope is ⅓ step where the step is 360° divided by

the number of facets.

Figure 7: Approximation error vs rotation angle.

3.3 Examples

The explicit expressions were used for several cases.

In all cases β was set to 30º. For simplification, the

space metric was scaled by the distance between the

axes and the apexes were set on the minimum vector

between the axes. The maximum possible distance

for surface-to-surface is then unity.

Figure 8 shows the minimum distance versus

positioning angle for various values of α (color-

coded).

Figure 8: Scaled minimum distance vs axes angle.

Figure 9 shows the distance along the A-axis

versus positioning angle for various values of α

(color-coded). In both Figures 8 and 9, the transition

to a constant value at the critical positioning angle

crit

is marked with vertical lines with matching

colors. For α=0, A-cone is a straight line.

0 30 60 90 120 150 180

0.05

0.1

0.15

0.2

Gama [deg]

errDmin [-]

Beta=30

Alpha=30

N-facet = 6

N-facet = 12

N-facet = 18

ombo=1/3 step: errDmin vs Omega

0 10 20 30 40 50 60

0.05

0.1

0.15

0.2

Omega [deg]

errDmin [-]

Beta=30

Alpha=30

N-facet = 6

N-facet = 12

N-facet = 24

ombo=1/3 step: errDmin vs Omega

0 30 60 90 120 150 180

0.2

0.4

0.6

0.8

Scaled Minimum Distance vs Gama

Gama [deg]

Min.Dist. [-]

Alpha=

Beta=30

GRAPP 2010 - International Conference on Computer Graphics Theory and Applications

158

Figure 9: Intersection A-distance vs axes angle.

Figure 10 shows the minimum distance error due

to a parametric error of 10 in α. From observing the

shape and starting point of the minimum distance

(see Figure 8), it is obvious there is a region with an

indefinite error in the minimum distance (the cones

intersect in this region). It should be noted that the

solution itself is exact, and it is the parametric error

that is propagated into the minimum distance.

Figure 10: Scaled minimum distance error vs axes angle.

4 CONCLUSIONS

Explicit expressions were derived for the minimum

distance between two solid semi-infinite circular

cones. The derivation is based on geometric

reasoning and vector algebra. Special regions and

cases were identified and discussed. A numerical

method based on minimizing the distance between

two generators was used as part of the verification

process. The exact solution was compared to results

of approximation by regular polytopes. The explicit

solution is robust, independent of coordinate system

and invariant under rigid translation and rotation of

the setup.

Future work will extend the scope of the problem

to include shells of finite cones. Shells require a

solution for a cone with generator angle larger than

π/2. Finite cones enlarge the set of solution types to

include the bases of the cones (contours and

surfaces).

REFERENCES

Gilbert, E. G., Johnson, D.W. and Keerthi, S.S., 1988, “A

Fast Procedure for Computing the Distance Between

Complex Objects in Three-Dimensional Space,” IEEE

Journal of Robotics and Automation, Vol. 4, No. 2, pp.

193-203, April 1988.

Jovanoski, D., 2008, “The Gilbert–Johnson–Keerthi

(GJK) Algorithm,” Department of Computer Science

University of Salzburg, February 2008.

Manchem, S. and Mukund, R., 2009, “The Gilbert-

Johnson-Keerthi Algorithm,” Indian Institute of

Technology Guwahati, October 31, 2009.

Chung, K. and Wang, W., 1996, “Quick Collision

Detection of Polytopes in Virtual Environments,”

ACM Symposium on Virtual Reality Software and

Technology 1996, 1-4, July, 96, University of Hong

Kong, Hong Kong.

0 30 60 90 120 150 180

0.5

1.5

A-Dist vs Gama

Gama [deg]

A-Dist [-]

Alpha=

Beta=30

0 30 60 90 120 150 180

0.1

0.2

0.3

0.4

0.5

0.6

0.7

Scaled Minimum Distance Error vs Gama

Gama [deg]

Min.Dist.Error [-]

Alpha=

Beta=30

Alpha Error=10

EXPLICIT SOLUTION FOR THE MINIMUM DISTANCE BETWEEN TWO SOLID SEMI-INFINITE CIRCULAR

CONES

159