
REAL-TIME CAMERA POSE ESTIMATION USING
CORRESPONDENCES WITH HIGH OUTLIER RATIOS
Solving the Perspective n-Point Problem using Prior Probability
Tobias N
¨
oll, Alain Pagani and Didier Stricker
Augmented Vision, DFKI, Trippstadterstr. 122, D-67663 Kaiserslautern, Germany
Keywords:
Real-time camera pose estimation, Low quality correspondences.
Abstract:
We present PPnP, an algorithm capable of estimating a robust camera pose in real-time, even if being provided
with large sets of correspondences containing high ratios of outliers. For these situations, standard pose
estimation algorithms using RANSAC are often unable to provide a solution or at least not in the required
time frame. PPnP is provided with a probability distribution function which describes all valid possible camera
pose estimates. By checking the correspondences for being compatible with the prior probability, it can be
decided effectively at a very early stage, which correspondences can be treated as outliers. This allows a
considerably more effective selection of hypothetical inliers than in RANSAC. Although PPnP is based on a
technique called BlindPnP which is not intended for real-time computing, a number of changes in PPnP allows
to estimate a camera pose with the same high quality as BlindPnP while being considerably faster.
1 INTRODUCTION
In this paper, we address the problem of camera pose
estimation from correspondences. Our goal is to find
a solution for the Perspective n-Point (PnP) problem
for correspondences with high ratios of outliers in
real-time.
Usually the camera pose for a given image is es-
timated solely using a set of n correspondences. A
large amount of different markerless pose estimation
algorithms already exists. Those algorithms presented
in (Dhome et al., 1989), (Fischler and Bolles, 1981),
(Gao et al., 2003), (Haralick et al., 1994), (Quan and
Lan, 1999) typically search for the roots of an eight-
degree polynomial with no odd terms. Their complex-
ity varies from O(n
2
) to even O(n
8
). In (Lepetit et al.,
2009) a method called EPnP (Efficient Perspective n-
Point Camera Pose Estimation) is proposed which al-
lows the computation of an accurate and unique solu-
tion in O(n) for n ≥ 4.
In practice, the estimation of the camera pose is
problematic if solely relying on the correspondences:
Often correspondences are established automatically
using feature detectors and a certain amount will be
misleadingly classified (outliers). In order to identify
and exclude the outliers, stochastic approaches such
as RANSAC (Fischler and Bolles, 1981) have been
developed. However RANSAC tends to fail or needs
an unacceptable large iteration count especially if the
outlier ratio grows.
In (Moreno-Noguer et al., 2008) a method to com-
pute the camera pose from correspondences called
BlindPnP is developed which integrates additional in-
formation beside the correspondences. BlindPnP as-
sumes that only two sets of 3D points and 2D points
are given without any correspondences. As additional
input, BlindPnP uses a probability distribution regard-
ing the final camera pose estimate (pose prior proba-
bility). This prior probability is then used to estab-
lish a camera pose and the corresponding correspon-
dences in parallel.
BlindPnP delivers good results even if no cor-
respondences are given at all. However due to its
slow runtime performance, BlindPnP is not applica-
ble in real-time reactive systems. The authors men-
tioned, that BlindPnP can be modified for using cor-
respondences without providing results of this modi-
fication. We called this modified version BlindPnPC
(BlindPnP with correspondences) and implemented
and evaluated it in order to check whether it is appli-
cable for real-time camera pose estimation. We will
show, that BlindPnPC delivers high quality solutions,
even if being provided with low quality correspon-
dences. However the experiments also showed, that
the runtime of BlindPnPC highly depends on n. As
n grows, BlindPnPC is not able to provide solutions
381
Nöll T., Pagani A. and Stricker D. (2010).
REAL-TIME CAMERA POSE ESTIMATION USING CORRESPONDENCES WITH HIGH OUTLIER RATIOS - Solving the Perspective n-Point Problem
using Prior Probability.
In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 381-386
DOI: 10.5220/0002850403810386
Copyright
c
SciTePress

in real-time. To also provide solutions in real-time
for large values of n, we developed a new algorithm
called PPnP (Prior probability Perspective n-Point
Camera Pose Estimation) based upon BlindPnPC. We
will show, that PPnP is capable of estimating a robust
camera pose even though being provided with sets of
noisy correspondences having high outlier ratios. We
will also show, that PPnP reaches both higher pre-
cision and speed than the comparable conventional
RANSAC+EPnP method as well as the prior proba-
bility based BlindPnPC method.
The remainder of this paper is organized as fol-
lows: Section 2 summarizes the underlying theory
used for BlindPnPC. Section 3 covers the concept
and implementation of PPnP. In section 4 we provide
quality and performance analyses of both algorithms
using synthetic and real data scenarios. We finally
conclude in section 5 with an outlook to future work.
2 PNP WITH PRIOR
INFORMATION
PPnP has similar concepts as BlindPnPC. This algo-
rithm is explained in detail in (Moreno-Noguer et al.,
2008). The underlying theory is summarized in this
section.
Let C be the set of correspondences, containing a
ratio of λ outliers. Our aim is to find the true cam-
era pose P =
R | t
as well as the set of inliers. Each
camera pose Q can also be parametrized as a 6 di-
mensional vector x
Q
. Let V be the pose prior prob-
ability which describes all valid parameterizations of
possible solutions Q. V is modeled using a Gaussian
mixture model with a number of g Gaussian compo-
nents. Each of the Gaussian components consists of
a mean value x
Q
∈ R
6
along with a covariance matrix
Σ
Q
∈ R
6×6
. Figure 1 gives an example of a possible
modeling. For simplicity, only the translation uncer-
tainty is visualized (green ellipsoids). The mean val-
ues x
Q
hereby specify the position, the covariances
Σ
Q
the shape of the ellipsoids. A real pose prior prob-
ability would normally consist of a 6D covariance.
Let M
Q
⊆ {P
i
←→ p
i
| i ∈ {1, . . . , n}} be the
set of pairs that match under the assumption that Q
is the correct pose. Let additionally F
Q
= C \ M
Q
be
the set of correspondences for which no match can be
established hypothesizing pose Q. The correct pose is
found by minimizing the error function E
E(x
Q
)
def
=
∑
P
i
←→p
i
∈M
Q
kp
i
− Pro j
x
Q
(P
i
)k + θ|F
Q
| (1)
with Pro j
x
Q
(P
i
) defined as the projection of P
i
on the
Figure 1: Modeling the camera pose prior probability by
mixtures of Gaussians.
image using pose x
Q
and θ ∈ R as a penalty term
that penalizes unmatched points. The minimization
is computed by utilizing the prior probability.
Roughly summarized, in each iteration Blind-
PnPC hypothesizes consecutively three 3D to 2D
point correspondences which are compatible with the
prior probability. Since the camera pose x
Q
has an
uncertain position indicated by the covariance Σ
Q
,
there exists also an uncertainty Σ
i
Q
regarding the po-
sition of the projected points which can be calcu-
lated by error propagation using the Jacobian J
i
Q
of
Pro j
x
Q
(P
i
). A correspondence is marked as compati-
ble with the prior probability if its projected 3D point
lies within that uncertainty Σ
i
Q
around p
i
. Hypothesiz-
ing of one correspondence is realized using a Kalman
filter. Hereby the 6 dimensional pose parameter is
interpreted as the system state and each correspon-
dence is interpreted as a measurement. During this
process, the camera pose x
Q
evolves and the assigned
covariance Σ
Q
(i.e. uncertainty) reduces. After three
correspondences are hypothesized, the remaining cor-
respondences can be checked for validity using this
camera pose by projecting the 3D points P
i
on the im-
age and checking the distance to their corresponding
2D point p
i
. This way the sets M
Q
and F
Q
can be con-
structed. The pose with the least error function value
E(x
Q
) is then chosen as result.
Discussion. We ran a number of experiments with
different ratios of outliers and compared BlindPnPC
to usual pose estimation approaches. As a represen-
tative common pose estimation approach we chose
RANSAC combined with EPnP (RANSAC+EPnP).
The experiments conducted showed, that by effec-
tive usage of the prior probability, BlindPnPC esti-
mates high quality results, mostly independent of the
outlier ratio. However for low outlier ratios, RAN-
SAC+EPnP outruns BlindPnPC in precision. Addi-
tionally, the runtime of BlindPnPC grows very fast
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
382

with the number n of correspondences used. This pro-
hibits an application in real-time reactive systems. We
present the results of these experiments in detail in
section 4.
3 NEW APPROACH
To overcome the problems of BlindPnPC, we de-
veloped an algorithm called PPnP which utilizes the
prior probability similar to BlindPnPC in order to ef-
fectively reduce the search space of the correspon-
dence problem.
3.1 Idea
Similar to BlindPnPC, in PPnP consecutively a num-
ber of correspondences which are valid with respect to
the prior probability are hypothesized using a Kalman
filter. Thereby the camera pose evolves from its initial
position.
BlindPnPC. Problematic in BlindPnPC is that each
consecutively selected correspondence has to be valid
in order to converge towards the real pose. If once
in BlindPnPC a wrong hypothesis is made, the pose
evolves in a bad way because future hypotheses cho-
sen will be outliers with a higher probability.
Hypothesizing an outlier will always badly affect
the current pose estimation Q. When projecting the
3D points P
i
and constructing the image projection
covariance Σ
i
Q
, many inliers previously correctly clas-
sified will now be marked as outliers and thereby not
be considered in the next selection process. Addition-
ally, by badly evolving the pose, outliers can now be-
come compatible with the current pose prior proba-
bility and are therefore treated as hypothetical inliers.
Combined, these effects lead to an increased outlier
ratio for the hypothesizing possibilities in the next
selection process. Thereby an outlier is also chosen
in the next selection process with a higher probabil-
ity, evolving Q even worse. BlindPnPC tries to solve
this issue by recursively hypothesizing all arguable
sequences of compatible correspondences containing
only three elements and selecting the one with the
least error function value. Thus a very large number
of consecutive hypotheses has to be made.
PPnP. PPnP tries to solve this issue by using a dif-
ferent approach: Consecutively a number of c corre-
spondences are hypothesized. Similar to BlindPnPC,
hypothesizing a correspondence P
i
←→ p
i
is realized
using a Kalman filter. Different than in BlindPnPC,
c is usually a number much higher than three. While
in BlindPnPC the whole sequence of hypotheses has
to be free of outliers, this is not a necessary condi-
tion for PPnP: At each step, all hypothesizing pos-
sibilities are stored for future use along with the un-
certainty information Σ
i
Q
and J
i
Q
. When it comes to
selecting a new hypothesizing candidate, it is ran-
domly selected from all available hypothesizing pos-
sibilities (containing also the ones not hypothesized in
the past). The key point is, that once an outlier is hy-
pothesized, the number m
i
of compatible candidates
when just considering the actual pose probability at
hypothesizing step i is relatively small compared to
the number of all hypothesizing possibilities from the
previous steps m
old
def
=
∑
i−1
j=0
m
j
. Since in the past a se-
quence of correct hypotheses was made, the majority
of all previous hypothesizing possibilities will contain
correctly identified inliers. Since the new hypothesis
is randomly chosen among all those m
new
def
= m
old
+m
i
possibilities with approximately m
old
correct hypoth-
esizing possibilities and only approximately m
i
out-
liers misleadingly classified as inliers, a correct cor-
respondence is selected with a relatively high prob-
ability. Hence, if an outlier is hypothesized at step
i, PPnP selects with a high probability an inlier for
the next candidate and thereby pushes the wrongly
evolved pose back to a valid state.
To gain a similar precision as RANSAC+EPnP,
the final camera pose estimate is only used in order
to classify M
Q
and F
Q
. M
Q
is then used in order to
calculate a high precision solution using EPnP.
Combined, this allows evolving the pose from a
relatively small fixed number of hypothesizing se-
quences containing c correspondences, instead of
considering each permutation combination of three
correspondences.
3.2 Optimization
Accelerating the Hypothesizing Process. Before
a correspondence from all available possibilities is
randomly selected for hypothesizing, all correspon-
dences are checked for validity with the current pose
prior probability. The information of each compat-
ible correspondence is then added to the set of se-
lectable options. If the number of correspondences
grows, the procedure of testing each correspondence
at each step for validity may lead to large overhead.
Fortunately this procedure can be optimized: A cor-
respondence being invalid with the pose prior proba-
bility at step i is unlikely to become valid in later steps
i + 1, i + 2, . . . because the overall reprojection uncer-
tainty reduces. This way, one can skip the successive
testing for validity of a certain correspondence, once
REAL-TIME CAMERA POSE ESTIMATION USING CORRESPONDENCES WITH HIGH OUTLIER RATIOS -
Solving the Perspective n-Point Problem using Prior Probability
383
it has been declared as invalid. Also it became appar-
ent that the correspondences chosen for hypothesiz-
ing at step i need not to be tested for validity again
at later steps. Thereby the computation can be eased
by keeping an exclusion list containing the correspon-
dences which will not be checked for validity with the
pose prior probability in later steps. The exclusion list
contains the correspondences already hypothesized or
once marked as invalid.
Optimizing the Hypothesis Picking Process. The
more information from steps far beyond the current
step is hypothesized, the slower the pose will con-
verge to its correct position. In order to select the
hypothesizing possibilities with the right balance be-
tween previous and current possibilities, all available
possibilities are kept in a list, linearly ordered accord-
ing to their degree of uncertainty (i.e. hypothesizing
possibilities appearing at later steps are pushed at the
end of the list). If a correspondence is randomly cho-
sen from that list, this is not realized uniformly but
with a probability linearly increasing towards the end
of the list.
4 EXPERIMENTS
4.1 Synthetic Test Setting
In order to compare the different approaches, the al-
gorithms are evaluated with respect to quality ε and
runtime performance µ. ε is measured in terms of
the mean reprojection error in pixel. µ is simply the
time in milliseconds it needs to find any solution. In
our scenario we assumed that the camera was located
somewhere inside a torus around the object in focus
and approximately directed towards it. The diame-
ter of the torus hereby defines the degree of uncer-
tainty with respect to the cameras’ position. This sce-
nario was modeled using a Gaussian mixture model
of g = 20 Gaussian components. We then constructed
a set C of n correspondences having an outlier ratio of
λ. We added normal distributed values up to 5 pixel
to the 2D points in order to simulate noise.
4.1.1 Results
Due to the large number of required hypothesizing
combinations, BlindPnPC suffers from a high run-
time, allowing a profitable use of the pose prior prob-
ability only for outlier ratios of 60% and above. If
an outlier ratio of 80% and above is reached, Blind-
PnPC and PPnP both are the only algorithms evalu-
ated which still are able to estimate a robust camera
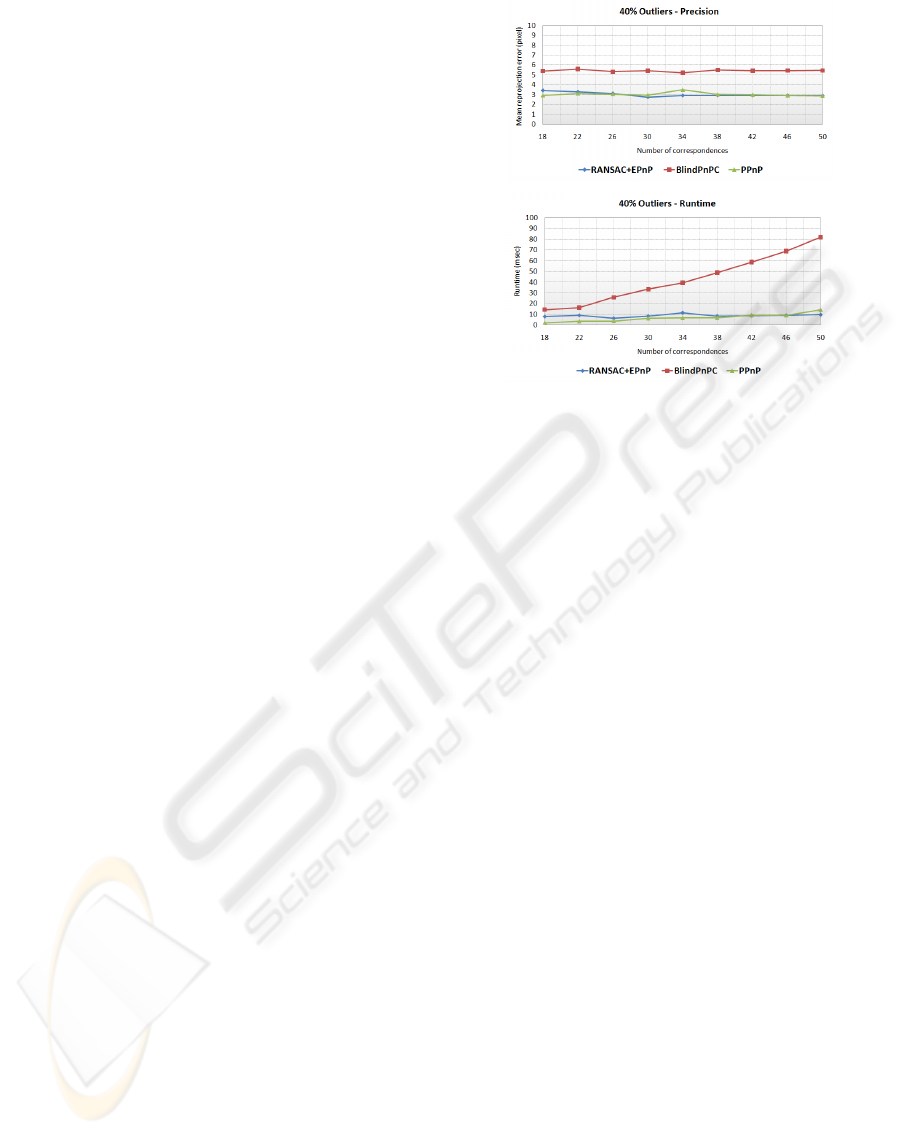
Figure 2: 40% outlier ratio measurement results.
pose. For these large outlier ratios the prior probabil-
ity seems to be crucial in order to estimate a reliable
camera pose.
For low outlier ratios, BlindPnPC consequentially
returns camera pose estimations with larger repro-
jection errors than the corresponding estimations of
RANSAC+EPnP. This is related to the fact, that only
three Kalman filter iterations are applied to evolve the
pose. However this unnecessary error is still tolerable
since it could be easily decreased by numerical opti-
mization techniques without significantially increas-
ing the runtime.
PPnP uses EPnP in order to gain results of sim-
ilar precision as RANSAC+EPnP for low outlier ra-
tios. Additionally, PPnP is implemented in an itera-
tive way, runs with a fixed number of iterations and
is thereby considerably faster than BlindPnPC. This
way the runtime can be lowered to a level which al-
lows an efficient usage of pose prior probability for
outlier ratios of 40% and above.
The measurements taken in the experiment are
displayed in Figures 2, 3 and 4.
4.2 Real Data Test Setting
A real data test setting was constructed with the inten-
tion to acknowledge the results gained in the synthetic
test setting:
Scenario. The scene filmed by the camera (640 ×
480, 30fps) was a desk. On the desk two images
with distinctive patterns were positioned whose coor-
dinates were known with respect to some coordinate
system.
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
384
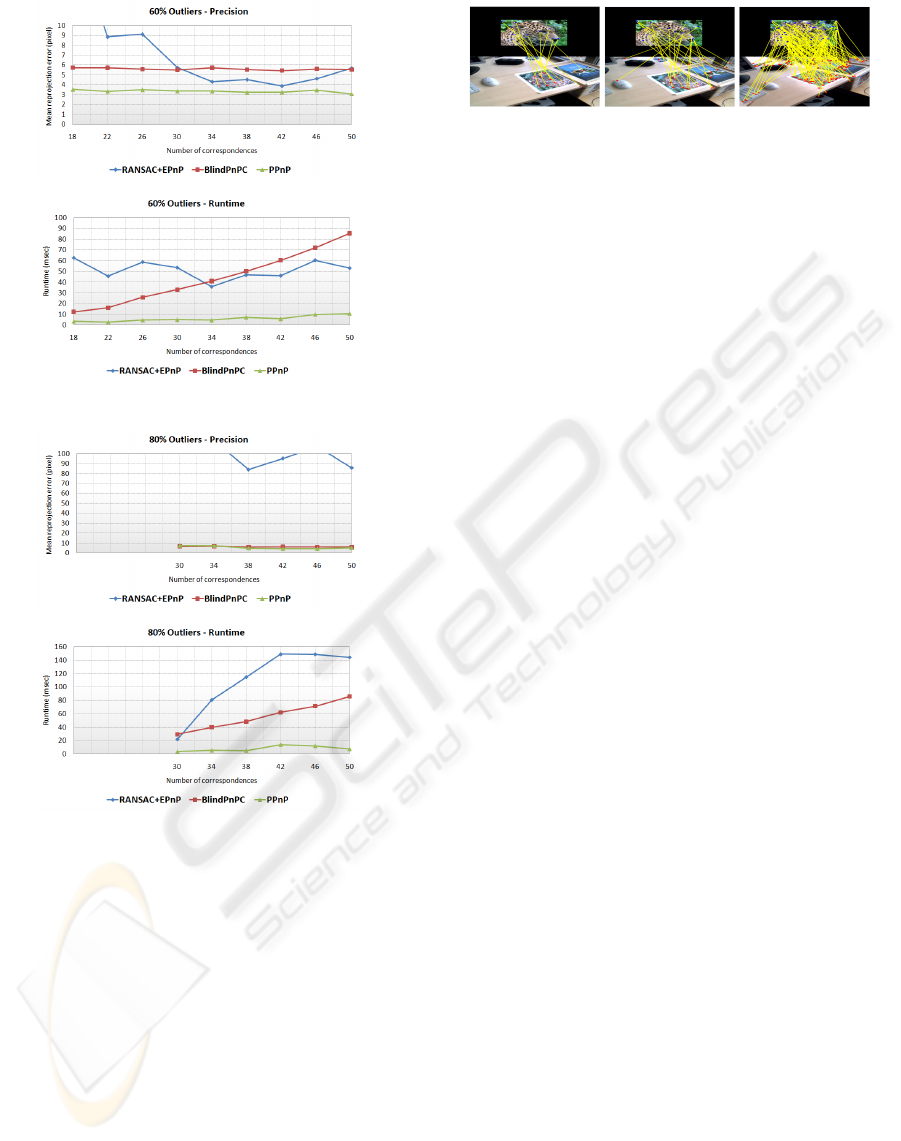
Figure 3: 60% outlier ratio measurement results.
Figure 4: 80% outlier ratio measurement results.
The prior probability V was established using a
Gaussian mixture model of g = 6 components as
sketched in Figure 1.
Correspondences. The correspondences were es-
tablished in real-time using randomized trees as clas-
sifiers. The technique is explained in detail in (Lepetit
et al., 2005). As seen in Figure 5 a threshold value τ
allows to control the certainty of the correspondences.
Because no ground truth camera pose is available
in a real data setting, we used the calculated set of
inliers I in order to check the quality. Using I as
provided by the respective algorithm, we used EPnP
for calculating a camera pose estimate Q. The border
rectangle of the object is then projected in yellow into
the scene using Q. This resulted in correctly framing
the object on the captured image if I was estimated
Figure 5: Threshold values τ from 0.1, over 0.05 to 0 control
the quality of the correspondences. This results in outlier
ratios ranging from λ ≈ 30% over λ ≈ 60% up to λ ≈ 80%.
correctly. Thus we were able to visually check the
integrity of I. As evidence of robustness, we counted
the frames where the inliers were correctly calculated.
We consider an algorithm as ‘robust’, if I was cor-
rectly calculated for more than 90% of the frames.
For values less than 50%, an algorithm is considered
as ‘not robust’. Values between are considered as ‘in-
termediate robust’. Based on I we also calculated the
average outlier ratio λ
≈
.
4.2.1 Results
Three experiments with different values for the cor-
respondence generator threshold τ were made. The
results are presented in Table 1.
Summarized, the experiments using a real data test
setting confirmed the results deduced from the syn-
thetic test settings. Standard methods such as RAN-
SAC+EPnP only deliver reliable results for small out-
lier ratios λ. As λ grows, standard methods tend to
fail or require an unacceptable large RANSAC itera-
tion count in order to deliver results at all.
BlindPnPC and PPnP use the available pose prior
probability and thereby are significantly less error
prone and faster than the standard methods. The esti-
mations computed by BlindPnPC and PPnP are both
robust and comparable. A difference however exists
with respect to runtime performance: Especially if n
is large, PPnP is able to provide results much faster.
Images series taken from the test setting using low
quality correspondences (τ = 0) with PPnP are shown
in Figure 6. Hereby the correspondences detected by
the feature detector are represented as red and green
dots. Red dots have been declared as outliers using
the respective algorithm, green dots as inliers.
5 CONCLUSIONS
In this paper we developed and evaluated a new al-
gorithm called PPnP, capable of estimating a robust
camera pose in real-time even though being provided
with large sets of noisy correspondences having high
outlier ratios. PPnP is based upon BlindPnPC which
we also implemented and evaluated. Both algorithms
REAL-TIME CAMERA POSE ESTIMATION USING CORRESPONDENCES WITH HIGH OUTLIER RATIOS -
Solving the Perspective n-Point Problem using Prior Probability
385
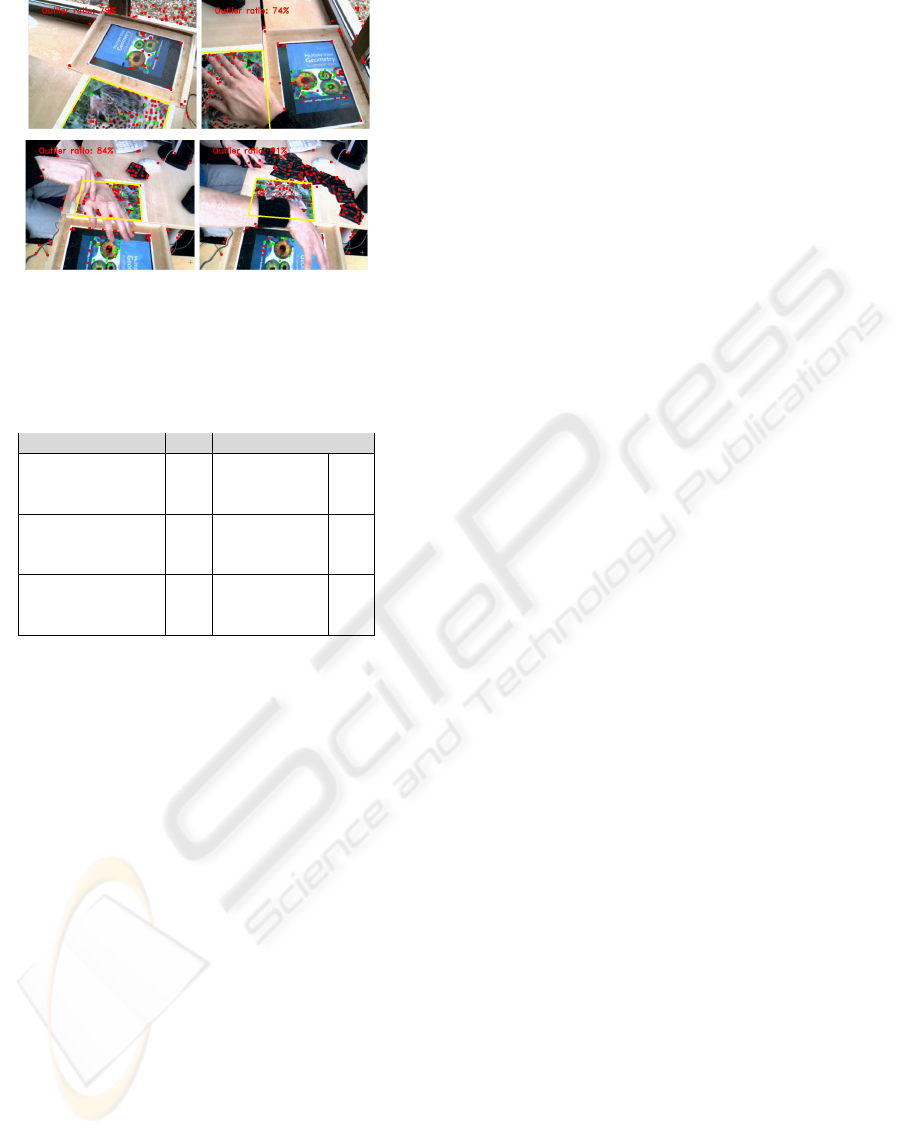
Figure 6: PPnP: High number of correspondences, high out-
lier ratio. A correct camera pose estimation is possible in
95% of the cases within at most 20 iterations. Even for
outlier ratios larger than 90% and in occurence of partial
occlusions, PPnP delivers reliable results. Speed: 25 fps.
Table 1: Real data test setting results.
Algorithm λ
≈
Robustness fps
0.3 Yes 30
RANSAC+EPnP 0.6 Intermediate 6
0.8 No 2
0.3 Yes 30
BlindPnPC 0.6 Yes 15
0.8 Yes 4
0.3 Yes 30
PPnP 0.6 Yes 30
0.8 Yes 25
use a probability distribution as additional informa-
tion beside the correspondences in order to handle
correspondences with high ratios of outliers.
In both synthetic and real data test settings we
have shown, that as the ratio of outliers grows, stan-
dard pose estimation approaches using RANSAC fail
in providing a robust camera pose estimate. In con-
trast to this, BlindPnPC and PPnP provide reliable re-
sults independent of the outlier ratio in the correspon-
dences. The pose prior probability allows BlindPnPC
and PPnP to ease the direct dependency of the esti-
mated camera poses’ quality on the ratio of outliers.
This direct dependency on the input data represents
the major weakness of standard methods.
In contrast to BlindPnPC – as the number of corre-
spondences used is raised – PPnP still is able to pro-
vide reliable results in real-time for these situations.
This is related to the optimization techniques intro-
duced in PPnP which allow to evolve the camera pose
requiring a much smaller number of consecutive hy-
pothesizing steps than in BlindPnPC.
5.1 Future Work
In our experiments both BlindPnPC and PPnP showed
good results. We would like to investigate, in how far
these algorithms can replace standard pose estimation
techniques in practice. Comparing to standard meth-
ods, BlindPnPC and PPnP depend on a large number
of variables which have to be assigned for each situ-
ation accordingly (e.g. pose prior probability, thresh-
old values, iteration count, . . .). Since these variables
are mutually dependent, the assignment is not intu-
itive and usually a certain effort has to be put into test-
ing different assignments before using the algorithms
appropriately. Hence additional techniques should be
developed, intending in improving the usability.
ACKNOWLEDGEMENTS
This work has been partially funded by the project
CAPTURE (01IW09001) and the German BMBF
project AVILUSplus (01M08002).
REFERENCES
Dhome, M., Richetin, M., Laprest
´
e, J.-T., and Rives, G.
(1989). Determination of the attitude of 3-d objects
from a single perspective view. In IEEE Transactions
on Pattern Analysis and Machine Intelligence, Vol. 11.
Fischler, M. A. and Bolles, R. C. (1981). Random sample
consensus: A paradigm for model fitting with applica-
tions to image analysis and automated cartography. In
Communications of the ACM, Vol. 24.
Gao, X.-S., Hou, X.-R., Tang, J., and Cheng, H.-F. (2003).
Complete solution classification for the perspective–
three–point problem. In IEEE Transactions on Pattern
Analysis and Machine Intelligence, Vol. 25.
Haralick, R. M., Lee, C.-N., Ottenberg, K., and N
¨
olle, M.
(1994). Review and analysis of solutions of the three
point perspective pose estimation problem. In Inter-
national Journal of Computer Vision, Vol. 13.
Lepetit, V., Lagger, P., and Fua, P. (2005). Randomized
trees for real–time keypoint recognition. In IEEE
Computer Society Conference on Computer Vision
and Pattern Recognition, Vol 2.
Lepetit, V., Moreno-Noguer, F., and Fua, P. (2009). EPnP:
An accurate O(n) solution to the PnP problem. In In-
ternational Journal of Computer Vision, Vol. 81.
Moreno-Noguer, F., Lepetit, V., and Fua, P. (2008). Pose
priors for simultaneously solving alignment and cor-
respondence. In ECCV ’08: Proceedings of the 10
th
European Conference on Computer Vision.
Quan, L. and Lan, Z. (1999). Linear n–point camera pose
determination. In IEEE Transactions on Pattern Anal-
ysis and Machine Intelligence, Vol. 21.
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
386
