
3D RECONSTRUCTION USING PHOTO CONSISTENCY FROM
UNCALIBRATED MULTIPLE VIEWS
Heewon Lee and Alper Yilmaz
Photommetry Computer Vision Lab, Ohio State University, Columbus, OH 43210, U.S.A.
Keywords:
Photo consistency, Homography, 3D Recovery.
Abstract:
This paper presents a new 3D object shape reconstruction approach, which exploits the homography transform
and photo consistency between multiple images. The proposed method eliminates the requirement of dense
feature correspondences, camera calibration, and pose estimation. Using planar homography, we generate
a set of planes slicing the object to a set of parallel cross-sections in the 3D object space. For each object
slice, we check photo consistency based on color observation. This approach in return provides us with the
capability for expressing convex and concave parts of the object. We show that the application of our approach
to a standard multiple view dataset achieves comparably better performance than competing silhouette based
method.
1 INTRODUCTION
Three-dimensional (3D) reconstruction of the object
shape from multiple images has an important role in
many applications including: tracking (Yilmaz et al,
2006), action recognition (Yilmaz and Shah, 2008)
and virtual reality applications (Bregler, Hertzmann,
and Biermann, 2000). The recent availability of im-
age collection on the Internet and publicly available
applications such as Google Earth and Microsoft Pho-
tosynth has increased the popularity of research on 3D
recovery.
Several approaches achieve 3D shape recovery by
finding 3D locations of matching points in differ-
ent view images using camera calibration and pose
(Isidoro and Sclaroff, 2003). These methods require
a triangulation step, which backprojects points from
the image space to the object space. However, these
methods explicitly require camera pose and calibra-
tion require establishing high number of point corre-
spondences between the images. Due to perspective
distortions, variations of color across different views,
and different camera gains generate a high number of
correspondences.
In contrast, using segmented objects in the images
and their direct back-projections, which generate a vi-
sual hull (Slabaugh and Schafer, 2001) is more flexi-
ble and eliminates the requirement to establish point
correspondences. However, back-projections from
the image space to the object space still require cam-
era pose and calibration for all the images. Another
limitation of back-projection of the silhouette is that
recovered 3D object will not contain details of objects
such as convexities and concavities despite having a
high number of images. To overcome the limitations
of visual hull based methods, researchers have pro-
posed voxel coloring technique, which measures the
color consistency of projected 3D points to images
(Seitz and Szeliski, 2006). These methods label each
grid on the object space as opaque or transparent by
projecting each voxel to input images. These projec-
tions after check the consistency of the projected col-
ors. Each consistent voxel is then checked for visibil-
ity. These methods, however, need precise calibration
and pose information and may result in wrong sur-
faces due to occlusion problems in the visibility test.
In this paper, we propose new technique that elim-
inates the requirements for known camera calibration
and pose. Proposed object approach analyzes implicit
scene and camera geometry through a minimal num-
ber of point correspondences across images, which
are used to form virtual images of a series of hypo-
thetical planes and their relations in the images space.
This paper is an extension to our former paper us-
ing silhouette-based methods(Lai and Yilmaz, 2008),
which improves the recovered 3D considerably by in-
troducing the photo consistency check. Particularly,
the photo consistency check introduced in this paper
provides detailed 3D recovery of convexities and con-
cavities in the object surface.
484
Lee H. and Yilmaz A. (2010).
3D RECONSTRUCTION USING PHOTO CONSISTENCY FROM UNCALIBRATED MULTIPLE VIEWS.
In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 484-487
DOI: 10.5220/0002850504840487
Copyright
c
SciTePress

The paper is organized as follows. Section 2 intro-
duces the main concepts of proposed method. Particu-
larly, in subsections 2.1 and 2.2, we discuss homogra-
phy transformations between the images with respect
to hypothetical planes slicing the object space. In sub-
section 2.3, we introduce our approach, which utilizes
the color information across images to generate the
3D object shape. Section 3 compares silhouette-based
methods with those of the proposed method. We con-
clude in Section 4 and present directions for further
research.
2 SHAPE RECONSTRUCTION
In this section we provide a discussion on the pro-
jective geometry for estimating the relation between
multiple views. Using these relations, we generate
image of object slice along the direction normal to
the reference plane. We should note that, in our ex-
periments we select one of the image planes as the
reference plane such that the recovered shape is cor-
rect up to a projective scale. Finally, we check color
consistency within the all position of 3D object and
generate 3D object having volumetric information.
2.1 Relations between Images
Mapping from the object space to the image space
is governed by the camera matrix. Let the points in
the image space, x, and the object space be respec-
tively represented in the homogeneous coordinates by
x = (x, y, 1)
T
, and X = (X, Y, Z, 1)
T
,(Hartley and Zis-
serman, 2000). The projection from X to x,is gov-
erned by the projective camera matrix P which intro-
duces a scale factor λ due to projective equivalency of
points in the homogenous coordinates:
λx = PX (1)
Considering that X lies on plane at Z=0, which we re-
fer to as the ground plane, its projection to x simplifies
P to homography transform, H. Homography trans-
form provides a direct mapping between 3D plane and
the image plane. Conversely, H also can be written to
linearly map points between images:
x = HX
′
(2)
Note that this mapping introduces another scale
factor, s, which is different from the scale in equation
(1). Let two image points x
1
, x
2
and 3D point
X
1
there are corresponding points. The relations
described as x
1
=H
1
X
1
and x
2
=H
2
X
2
give rise to a
mapping between x
1
, x
2
is as:
x
1
= H
1
(H
2
)
−1
x
2
= H
12
x
12
(3)
Figure 1: The relation between 3D planes in the object
space and their images. A series of planes i parallel to
the reference plane intersect the object volume and generate
slices of the object.
2.2 Image of Object Slices
A stack of object slices when stacked together results
in the object shape recovered up to a projective scale.
We illustrate an instance of the conjecture in Figure 1,
where the relations between image with respect to the
object slices generated by hypothetical planes are de-
noted by H and H
′
, planar homography matrix. These
planes and homography transform of each of them on
to the images generate coherency maps, which in turn
provides the 3D object shape. Let each hypothetical
plane has its normal direction aligned with the Z-axis,
X
i
be the set of 3D points X
1
, X
2
, X
3
, and X
4
and X
′
i
be the set of 3D points X
′
1
, X
′
2
, X
′
3
, and X
′
4
, where X
′
i
andX
i
are corresponding points in hypothetical planes.
The image of the intersection of the lines connecting
where X
′
i
andX
i
provides us with the vertical vanish-
ing point as shown in Figure 1. Using equations (1)
and (2), the relation between points in two images can
be de-fined based on the height of the hypothetical
plane and the vertical vanishing point as:
λ
i
x
′
i
=
P
11
P
21
P
41
P
12
P
22
P
42
P
13
P
23
P
43
X
Y
1
+
P
31
P
32
P
33
Z (4)
= s
i
x
i
+V
z
Z
In this equation, λ
i
and s
i
are the scale factors
which are computed as elaborated in (Lai and Yil-
maz, 2008). In these equation, parameters λ
i
, s
i
, V
z
,
and Z are known and provides direct relations be-
tween x
i
and x
′
i
.
3D RECONSTRUCTION USING PHOTO CONSISTENCY FROM UNCALIBRATED MULTIPLE VIEWS
485
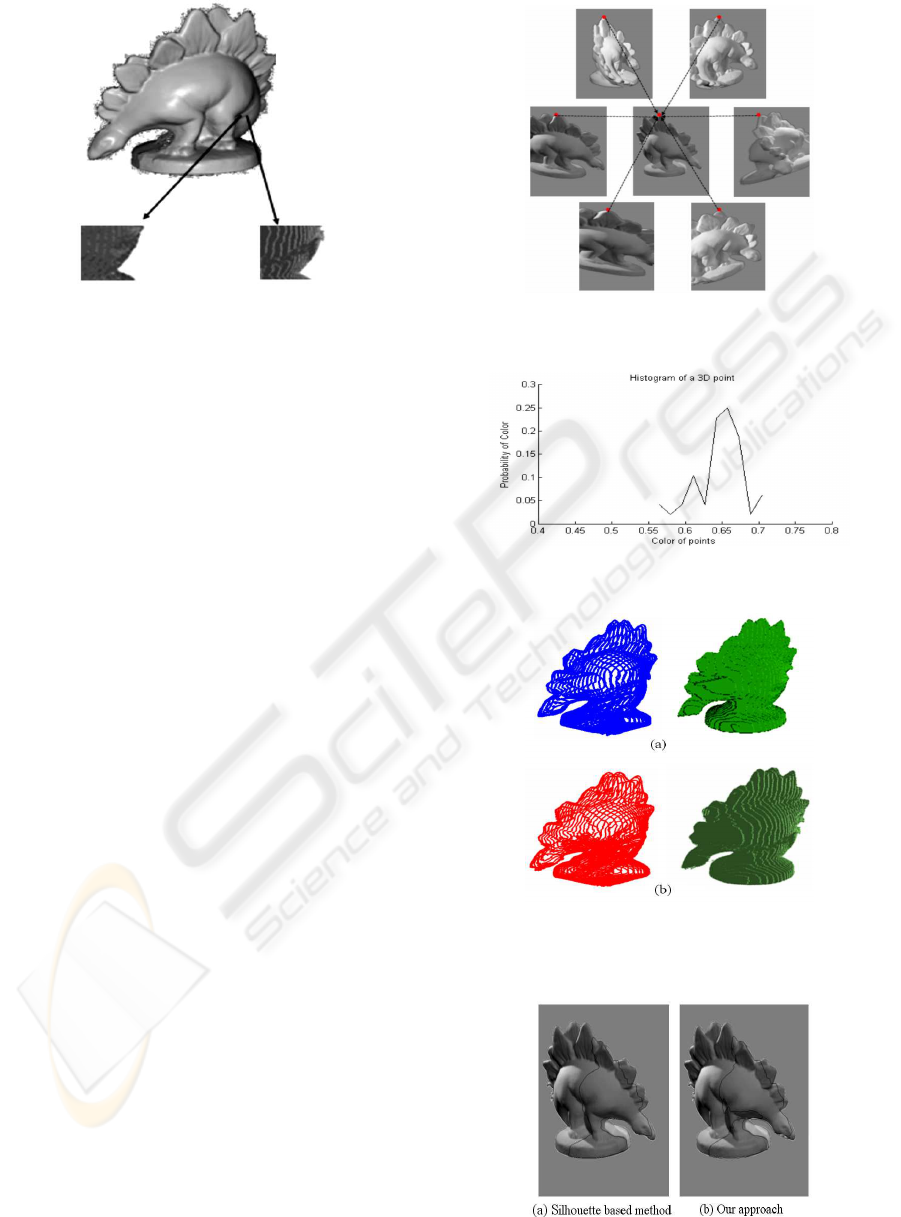
Figure 2: Concavities recovered using (left) silhouette
based and (right) proposed approaches on leg of dinosaur.
2.3 Reconstructing the Object Shape
In the recent silhouette based approach by Lai and
Yilmaz (2008), the indicator functions depicting the
objects have resulted in removal of the object shape
information implicitly encoded in the surface color.
Therefore, resulting 3D object shape excluded con-
vexities and concavities in the object surface. In
Figure 2, we present convexities on the leg part of
the dinosaur. A careful observation suggests that
the silhouette-based model (left) couldnt detect con-
cavities. In contrast, our approach (right) estimates
the concavities correctly.
In our approach, we utilize the distribution func-
tions of color observed in images in the form of kernel
density estimate. We assume that a 3D point project-
ing to images consistently has same color at corre-
sponding image pixels. By exploiting the relation in
equation (4), the kernel density estimate is generated
for corresponding image pixels using RGB bands as
shown Figure 3. In Figure 4, we show the kernel den-
sity estimate generated from 48 views of the dinosaur
object. According to the conclusion for color consis-
tency presented in (Slabaugh and Schafer, 2001), the
same point on object surface have similar color, hence
provides a peak in the density estimate. In contrast,
nonsurface points will have different colors and their
histograms will have many low valued local maxima.
3 EXPERIMENTAL RESULTS
We experimented with dinosaur and temple images
from the Middlebury multiview stereo dataset. Partic-
ularly, we compare our results with silhouette-based
method. Figure 5 shows the resulting 3D shape for
the dinosaur image set. In figure 5, (b) and (c) show
two different types shape recovery using plot and iso-
Figure 3: 3D point from multiple images warped to refer-
ence plane shown in the center.
Figure 4: KDE generated from corresponding image pixels
marked as dots in Figure 3 using 48 images.
Figure 5: Recovering the 3D shape of dinosaurs. The 3D
reconstructed object of silhouette-based method (a) and of
our approach (b).
Figure 6: Reference image with sliced results using differ-
ent methods of Z=-0.005.
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
486

Figure 7: 3D shape recovered using 33 images. (a) Example
image (b) two views of reconstructed shape.
surface function. In our results we used 0.005cm dis-
tance between the planes.
Comparing the silhouette based and proposed ap-
proaches, we observe that our approach can express
details convex and concave parts on the leg and body
part of the dinosaur effectively. This observation can
be seen in Figure 6, where we show one particular
slice superimposed on the dinosaur. As shown, the
silhouette based method fails to generate precise ob-
ject shape. Particularly, in part (a), the boundary from
the slice incorrectly involves the dinosaurs neck and
body parts. On the other hand, part (b), which is gen-
erated by our approach, estimates distinct concavity
parts from neck to body. To demonstrate 3D recovery
of a complex object, we conducted one last experi-
ment as shown in Figure 7. It shows that a object
having complex shapes are recovered with high per-
formance.
4 CONCLUSIONS
In this paper we propose to generate sliced images
based on photo consistency for 3D object shape
recovery from uncalibrated cameras. Differ from
silhouette-based methods, each image of object slices
utilizes the color observed in 2D images. The prob-
ability value of histogram shows 3D object surface
conditions such as concavity and convex. Without the
need for camera calibration and estimation and unnec-
essary visibility checks, we recover 3D using simple
linear mappings.
REFERENCES
Bregler, C., Hertzmann, A., and Biermann, H. (2000). Re-
covering non-rigid 3d shape from image streams. In
International Conference on Computer Vision. IEEE.
Hartley, R. and Zisserman, A. (2003). Multiple view geom-
etry in computer vision. Cambridge Univ Pr.
Isidoro, J. and Sclaroff, S. (2003). Stochastic refinement
of the visual hull to satisfy photometric and silhouette
consistency constraints. In IEEE International Con-
ference on Computer Vision. IEEE.
Khan, S. M., Yan, P., and Shah, M. (2007). A homographic
framework for the fusion of multi-view silhouettes. In
ICCV 07, 11th International Conference on Computer
Vision. IEEE.
Lai, P. and Yilmaz, A. (2008). Efficient object shape re-
covery via slicing planes. In CVPR 08, Conference on
Computer Vision and Pattern Recognition. IEEE.
Seitz, S., Curless, B., Diebel, J., Scharstein, D., and
Szeliski, R. (2006). A comparison and evaluation
of multi-view stereo reconstruction algorithms. In
CVPR06, Conference on Computer Vision and Pattern
Recognition. IEEE.
Slabaugh, G., Culbertson, B., Malzbender, T., and Schafer,
R. (2006). A survey of methods for volumetric scene
reconstruction from photographs. In n CVPR06, In-
ternational Workshop on Volume Graphics. IEEE.
Yilmaz, A., Javed, O., and Shah, M. (2006). Object track-
ing: A survey. ACM Journal of Computing Surveys.
Yilmaz, A. and Shah, M. (2008). A differential geomet-
ric approach to representing the human actions. Com-
puter Vision and Image Understanding Journal.
3D RECONSTRUCTION USING PHOTO CONSISTENCY FROM UNCALIBRATED MULTIPLE VIEWS
487
