
PROCESS MINING FOR JOB NETS
IN INTEGRATED COMPLEX COMPUTER SYSTEMS
Shinji Kikuchi, Yasuhide Matsumoto, Motomitsu Adachi
Fujitsu Laboratories Limited, Japan
Shingo Moritomo
Fujitsu Limited, Japan
Keywords: Process mining, Batch job, Job net, Integrated system, Behavior analysis.
Abstract: Batch jobs, such as shell scripts, programs and command lines, are used to process large amounts of data in
large scale enterprise systems, such as supply chain management (SCM) systems. These batch jobs are
connected and cascaded via certain signals or files so as to process various kinds of data in the proper order.
Such connected batch jobs are called “job nets”. In many cases, it is difficult to understand the execution
order of batch jobs in a job net because of the complexity of their relationships or because of lack of
information. However, without understanding the behavior of batch jobs, we cannot achieve reliable system
management. In this paper, we propose a method to derive a job net model representing the execution order
of the job net from its logs (execution results) by using a process mining technique. Improving on the
Heuristic Miner algorithm, we developed an analysis method which takes into account the concurrency of
batch job executions in large scale systems. We evaluated our analysis method by a conformance check
method using actual job net logs obtained from a large scale SCM system. The results show that our
approach can accurately and appropriately estimate the execution order of jobs in a job net.
1 INTRODUCTION
There are many cases where enterprise information
systems are constructed not by developing them
“from scratch”, but by connecting a large number of
smaller systems. For example, many supply chain
management (SCM) systems have been built by
interconnecting individual systems processing
different data such as production, sales & marketing,
and logistics. These individual systems have usually
been built at different times by different vendors
based on different policies. Therefore, integrating
and interconnecting different types of system can
result in a more complex system than one that has
been purpose built from the beginning. As a result, it
becomes very difficult to manage these integrated
systems such that their subsystems can not only
process their own data propery but also work
consistently with the other subsystems.
In this kind of integrated system, batch processes
called “jobs”, such as batch files, shell scripts and
commands, play important roles. These jobs are
executed in order to handle large amounts of data,
such as accounting or inventory checks, in contrast
with transaction processes which handle each
request from users as soon as it arrives. These jobs
can be scheduled and invoked by job net
management functions such as SystemWalker
Operation Manager (Fujitsu, 2008) which control
jobs and invoke them at a certain time such as
overnight or at the end of the month. After a job
finishes, it can invoke another job and hand over its
processing results via files or signals output from the
previous job. By invoking a job from another job
runnning on a different server or subsystem, we can
choreograph some subsystems to process their
common data in the proper order, as described in
Figure 1. Therefore, we can say that these batch jobs
play important roles in bridging the gap between
subsystems and connecting them so that the whole
system can process data properly. We call a set of
batch jobs concatenated and executed in a defined
order a “job net”.
5
Kikuchi S., Matsumoto Y., Adachi M. and Moritomo S. (2010).
PROCESS MINING FOR JOB NETS IN INTEGRATED COMPLEX COMPUTER SYSTEMS.
In Proceedings of the 12th International Conference on Enterprise Information Systems - Information Systems Analysis and Specification, pages 5-12
DOI: 10.5220/0002853500050012
Copyright
c
SciTePress
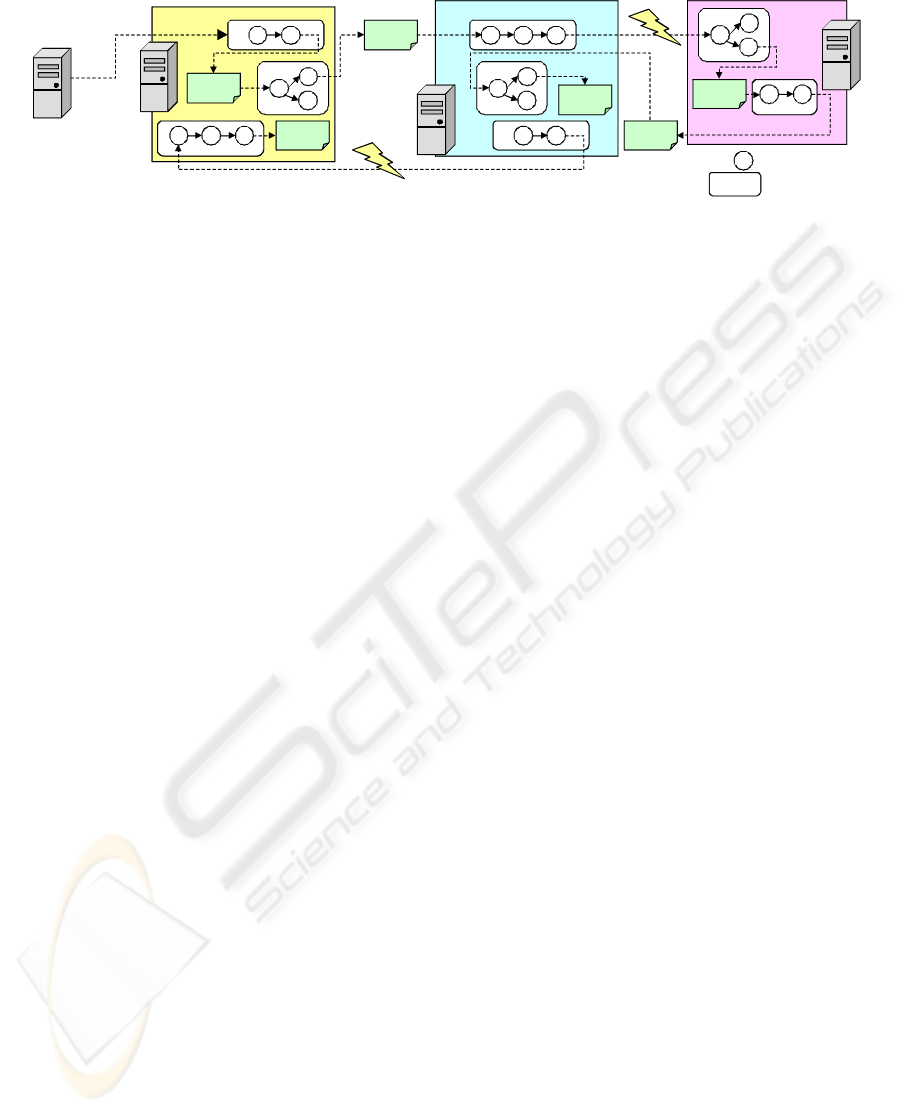
Marketing
File
File
File
… Batch job
File
File
File
Logistics Production
Job net
manager
Invoke
… Job net
Signal
Signal
Figure 1: Job nets connecting different systems via files and signals.
It is, however, extremely difficult to understand
the behavior and the execution orders of the jobs in
these kinds of “tangled” job nets, because the clues
to solving the problem are scattered everywhere. For
example, even if job scheduling information is
stored in several job net manager systems for the
invocation of jobs, they might be managed by the
administrator of a subsystem or by each individual
department. Because of this “silo” management,
access to this kind of information from outside the
department might be prohibited. In addition, in many
cases, the information regarding the triggers (files
and signals) invoking the jobs is embedded in the
job’s script or the program itself. Deriving the
information regarding the triggers from program
code analysis is practically impossible. For these
reasons, it is difficult to understand the behavior of
interrelated batch jobs. This problem can worsen in
the case of the integration of larger systems such as
M&A. However, without understanding the behavior
of job nets, we cannot achieve reliable service
management, such as predicting the finishing time of
jobs or determining which job was the root cause
when the execution of jobs are delayed. Therefore,
there is a strong need for a technique for
understanding the behavior of job nets.
Against this background, we developed an
analysis method to derive a model of job nets
representing their execution order from the job net
log recording their execution results by using a
process mining technique. In this method, we
improve the Heuristic Miner process mining
algorithm by taking into account the concurrent
execution of jobs. We then applied our method to
job net logs derived from an actual SCM system and
evaluated the accuracy of our approach by a
conformance check method.
The rest of this paper is organized as follows.
First, in Section 2, we survey related work. Next,
Section 3 explains our job net mining algorithm in
detail. We then show how it works through a case
study in Section 4 using an actual set of log data and
evaluate its performance. Following this, Section 5
concludes the paper and outlines future challenges.
2 RELATED WORK
One of the most important major techniques for
deriving the behavioral characteristics of systems is
the process mining approach (van der Aalst, 2007).
Process mining is a method of extracting the
information about a process from its execution
results (event logs) in order to construct a process
model that can represent the behavior of systems or
processes. The process model can be represented by
some state transition systems such as the Markov
model or Petri Net. Various algorithms for process
mining have been proposed so far, such as the alpha-
algorithm (van der Aalst, 2004) and genetic
algorithm (van der Aalst, 2005). These algorithms
are intended for application to the analysis of
business processes usually executed by human
beings and consisting of less than a dozen events.
The computational time for these algorithms
therefore tends to increase rapidly with the number
of events per process. While this does not matter
when the process consists of only a small number of
events, we can not apply these methods directly for
job net analysis since the job nets in large scale
systems can consist of hundreds of jobs.
Computational time for the Heuristics Miner
algorithm (Weijters, 2006) is relatively small
because of its simplicity and straightforwardness. It
is, however, possible that this simple algorithm
cannot achieve sufficient accuracy in job net
analysis for large systems where we have to take
into account the possibility that many jobs are
executed concurrently. There is therefore a strong
need for an algorithm that is specialized for job net
mining so as to achieve both short computational
time and sufficient accuracy.
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
6
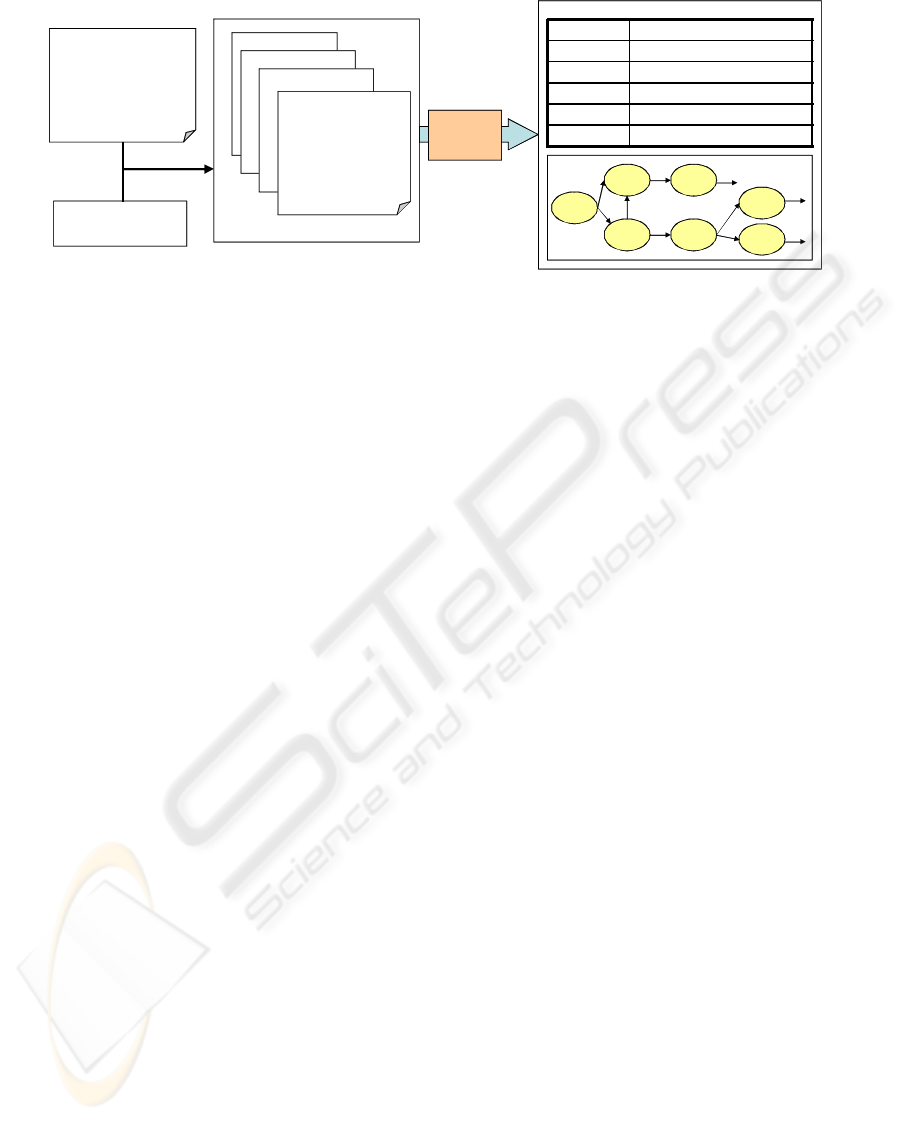
…..
3/1 00:00 Job1 Start
3/1 00:10 Job2 Start
3/1 00:15 Job2 End
…
3/31 23:40 Job53 End
3/31 23:50 Job89 End
Job net log (raw data)
(March 1st – 31st)
March 3rd
Target time window
Every night
( 0:00 - 6:00 am)
Instances
March 2nd
March 1st
3/1 00:00 Job1 Start
3/1 00:10 Job2 Start
3/1 00:15 Job2 End
…
3/1 05:58 Job35 End
Job net
Mining
Job net model ( output )
Event Likely following events
Job1(Start) Job1(End) xor Job2(Start)
Job2 (Start) Job2(End) xor Job1(End)
Job1 (End) Job3(Start)
Job2 (End) Job4(Start) and Job5 (Start)
…
Job1(S)
Job1(E)
Job2(S) Job2(E)
Job3(S)
Job4(S)
Job5(S)
XOR
XOR
AND
Figure 2: Input and output data for job net mining.
3 JOB NET MINING METHOD
In this section we explain our job net mining method
in detail. First, we define its data structure. Next, we
explain our mining algorithm based on the Heuristic
Miner algorithm with some improvements for taking
concurrency in batch job execution into account.
Then, we explain how the accuracy of our mining
method can be evaluated through a conformance
check approach.
3.1 Data Structure
Figure 2 summarizes the input and output data for
our approach. As explained in Section 1, in many
cases we cannot obtain or determine the location of
the information defining the schedules or
relationships of the batch jobs. Therefore, we
assume here that we can obtain only the job net
event logs which are output as the execution results
of these jobs. This kind of log is relatively easy to
obtain, since it is usually created so that the
administrators of job nets can diagnose their
behavior after a problem has occurred. We also
assume that the start time and end time of each job is
recorded in the job net logs. For simplicity, we
assume here that the granularity of the timestamp is
1 second and each job is executed no more than once
per day. In our analysis, we define the time window
(e.g. overnight, from 0:00 am to 6:00 am) on which
we focus attention. Then we extract the data within
the time window to be used for our analysis. We
refer to the sequence of log data for a job net
executed in the time window on a particular day as
an instance of the day.
The output from our method is a job net model
representing the common patterns of orders of
events emerging in many instances. Here we assume
that each event is either the beginning or the
finishing of a job recorded in the logs. The model
contains order relations between each preceding
event and a set of (likely) following events. It can be
represented by tables or directed graphs as shown in
the right hand part of Figure 2. If a preceding event
has more than two possible following events, we
should determine those branches as either an AND-
fork or an XOR-fork. The AND-fork means that all
of the following events will occur after the
preceding event, while the XOR-fork means that
only one of the following events will occur after the
preceding event.
3.2 Mining Algorithm
Since a large number of batch jobs may be executed
simultaneously in large scale systems consisting of
many servers, our analysis has to take the
concurrency in job net mining into account in order
that sufficient accuracy is achieved. We therefore
developed an algorithm consisting of the following
three steps. First, we determine the set of jobs which
are likely to start at the same time from timestamps
recorded in the log. Next, we derive the order of
events using the Heuristic Miner algorithm. Finally,
we modify the Heuristic Miner results using the
information regarding concurrent jobs derived in the
first step. The details of these steps are as follows.
Step 1: Concurrent Job Detection from
Timestamp
In the first step, we determine the set of jobs which
start at almost the same time for reasons such as the
preceding job triggering several following jobs, or
jobs happening to be scheduled to start at the same
time by different administrators. We use the
PROCESS MINING FOR JOB NETS IN INTEGRATED COMPLEX COMPUTER SYSTEMS
7
following evaluation functions to determine whether
jobs J
i
and J
k
are likely to start at the same time.
)(
)|)()((|
),(
i
pik
ki
JN
JSJSN
JJp
τ
<−
≡
(1)
)(
i
JN represents the number of instances
including execution of job J
i
.
)|)()((|
pki
JSJSN
τ
<−
represents the number of
instances in which the difference between the start
times of J
i
and J
k
is smaller than the threshold
p
τ
sec. We can say that J
i
and J
k
tend to start at the
same time if
),(
ki
JJp is close to 1.
Using equation (1), we define the set
)(
i
Jc of
jobs which are likely to start at the same time as job
J
i
.
}),(|{)(
ckiki
JJpJJc
τ
>≡
(2)
This means that if
),(
ki
JJp is larger than
c
τ
, J
k
is included in
)(
i
Jc .
Step 2: Event order Analysis by Heuristics Miner
Heuristics Miner (Weijters, 2006) is a process
mining algorithm which derives patterns in the order
of events from event logs independent of the events’
timestamps. This method determines the existence of
consecutive order relations between events using the
following function
kWi
ee ⇒
.
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+>+>
>−>
≡⇒
1||||
||||
iWkkWi
iWkkWi
kWi
eeee
eeee
ee
(3)
Function
||
kWi
ee >
represents a count of the
instances in which event e
i
’s next event was e
k
. Here,
we take into account only the order of events,
independent of timestamps. We consider that there is
an order relation between event e
i
and e
k
when the
function
kWi
ee ⇒ is over a given threshold. In our
analysis, we adopt an all-activities-connected-
heuristic that derives at least one preceding event for
each event. Here, we define two thresholds: (1)
Dependency threshold
D
τ
and (2) Relative to best
threshold
R
τ
. If
DkWi
ee
τ
>⇒ )( , we conclude that
there is an order relation between event e
i
and e
k
. If
event e
k
does not have any preceding event e
i
such
that
Dki
ee
τ
>⇒ )(
, we select an event e
x
such that
)()(
kWykWx
eeee ⇒≥⇒ for any other event e
y
.
We then consider that there is an order relation
between event e
i
and e
k
if
RkWxkWi
eeee
τ
−
⇒≥⇒ )()(
.
Next, we use the following function
kjWi
eee
∧
⇒
to determine whether the order
relations
kWi
ee ⇒
and
jWi
ee ⇒ from the same
event
i
e
represent an AND-branch or XOR-branch.
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+>+>
>+>
≡∧⇒
1||||
||||
kWijWi
jWkkWj
kjWi
eeee
eeee
eee
(4)
If the value of this function is larger than
threshold
A
τ
, we assume that the two relations are
AND-branches, meaning that both following events
will eventually occur after the preceding event
i
e
.
Otherwise, we conclude that they are XOR-branches,
i.e. that only one of the following events will occur
after the preceding event.
In our analysis, we assume each event to be
either the start event or end event of a job. In the
remainder of this paper, we denote the job J
i
’s start
event and end event by
S
i
e and
E
i
e respectively.
Step 3: Adjustment for Concurrency
After determining the sets of concurrent jobs in Step
1 and the jobs’ order relations in Step 2, we adjust
the results of the latter by those of the former’s in
Step 3.
i
e
S
k
e
1
Jobs start at
the same time
Result from Step 1 and 2
i
e
Jobs start at
the same time
AND-branch
Adjustment in Step 3
S
k
e
2
S
k
e
3
S
k
e
4
S
k
e
1
S
k
e
2
S
k
e
3
S
k
e
4
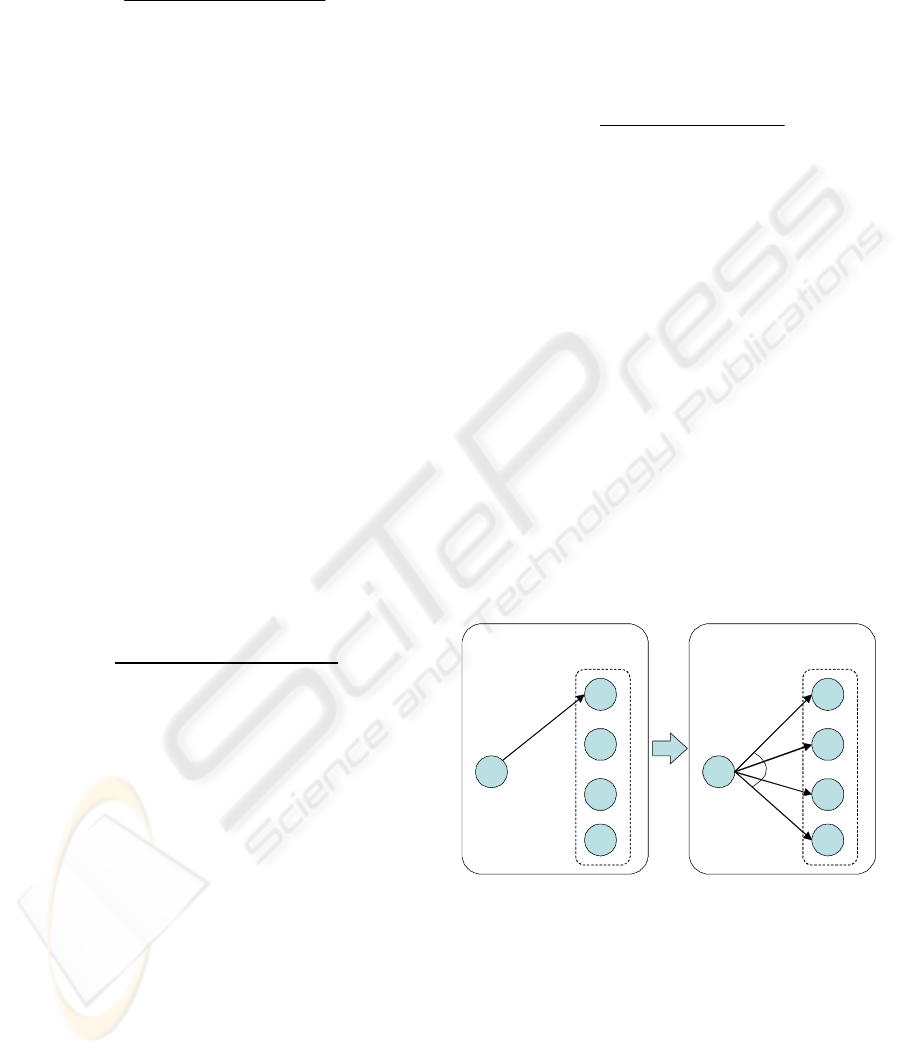
Figure 3: Adjustment in Step 3.
Figure 3 shows the general concept of the
adjustment. Here we suppose that Step 1 determined
that the set of jobs
1k
J
,
2k
J
,
3k
J
and
4k
J
start at
the same time. The corresponding start events of
these jobs are represented in the dotted rectangle by
S
k
e
1
,
S
k
e
2
,
S
k
e
3
,and
S
k
e
4
respectively. We also
suppose that the order relation from a preceding
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
8
event
i
e
to the start event of some of these jobs (e.g.
1k
J
) is determined by Step 2, as shown by the arrow
in the left hand part of Figure 3. In such cases,
while any jobs in the set of following jobs (
1k
J ,
2k
J ,
3k
J
and
4k
J
) can start after the preceding event
i
e
,
the relations between event
i
e
and the following
events other than
1j
e are not correctly detected by
the Heuristics Miner algorithm. It is difficult for
Heuristics Miner to correctly determine such
concurrencies because the occurrence of several
events at almost the same time can be recorded in
their logs in random order.
In order to solve this problem, we adjusted the
model derived in Step 2 using the results of Step 1 as
follows.
(1)
Select a relation
S
kWi
ee ⇒ and a set of
jobs
)(
k
Jc which start at the same time as
the start event
S
k
e of job
k
J .
(2)
Establish the order relations from the
preceding event
i
e to the start event of the
jobs in
)(
k
Jc .
(3)
Designate the relations thus established as
AND-branches
The result of this adjustment can be seen on the
right hand side of Figure 3. By performing this
adjustment in our model construction, we can take
into account the concurrent job information which
may be overlooked by the Heuristic Miner algorithm.
3.3 Conformance Check
In order to evaluate the accuracy of our mining
algorithm, described in Section 3.2, we use a
conformance check (Rozinat 2005, 2008) which
evaluates how well process models derived by a
process mining algorithm express the patterns
emerging in event logs by “replaying” the instances
of the logs on the obtained models and detecting
inconsistencies between the model and the logs.
The general concept of the conformance check is
shown in Figure 4. First, we prepare a process model
derived from a process mining algorithm. We also
prepare instances of logs for evaluation of their
conformance with the model. Next, we replay on the
model, one by one, the events recorded in the
instances. In this replay, we predict the candidates
for the next events following each preceding event
by referring the process model. For example, in the
Process model
No. Event Expected next events
1
2
3
4
…… …
1
e
2
e
3
e
4
e
5
e
6
e
7
e
AND
XOR
XOR
Instance A
00:00
00:05
00:08
00:10
…
1
e
2
e
4
e
6
e
1
e
2
e
4
e
6
e
2
e
3
e
3
e
4
e
7
e
3
e
3
e
8
e
8
e
Replay
Predict next events
Wrong !
Figure 4: Conformance Check.
case shown in Figure 4, after the first event
1
e
occurs in instance A, we predict that the next event
will be either
2
e
or
3
e
, because these events are the
following events for
1
e
in the process model.
Likewise, after the second event
2
e
occurs, we
predict one of the events
3
e
,
4
e
, or
7
e
will be the
third event. Here event
3
e
still remains as one of the
expected next events since the links
21
ee → and
31
ee →
are AND-branches meaning that both
2
e
and
3
e
can occur after the preceding event
1
e
.
Next, we check whether or not each prediction is
correct. We conclude that the model conforms to the
instance if the i-th event recorded in the instance is
included in the (i-1)-th expected next events
predicted by the model. In Figure 4, while the first
three events (
1
e ,
2
e and
4
e ) are predicted correctly,
the occurrence of the fourth event
6
e
is not
predicted by the model, because it is not included in
the third set of expected next events. If the number
of such events, those not expected by model, is small,
we can conclude that the model fits well with the
given instance. This fitness can be evaluated by the
following “fitness” function which is simplified
from the original functions (Rozinat 2005, 2008) so
that it suits the conditions in our job net analysis.
∑
∑
=
=
−=
k
i
i
k
i
i
n
m
f
1
1
1
(5)
In this fitness function, k represents the number
of instances used for the evaluation, n
i
is the number
of events recorded in the i-th instance and m
i
is the
number of events which are not predicted correctly
PROCESS MINING FOR JOB NETS IN INTEGRATED COMPLEX COMPUTER SYSTEMS
9
by the given process model. A value of the function
close to 1 indicates that the model fits well with the
given instances.
All the same, if we include all the events of the
instance in the set of expected next events, we can
always achieve a high value for the fitness function.
This, however, would be meaningless because it
does not narrow down the set of possible next events.
Therefore, the smaller number of expected next
events derived from a model, the closer that model
appropriately represents the structure of the process,
and the more valuable it is. To evaluate this
characteristic, we use the following
“appropriateness” function, which has also been
tailored to our purpose.
∑
∑
=
=
⋅−
−
=
k
i
i
k
i
ii
nM
xMn
a
1
1
)1(
)(
(6)
M is the number of events emerging in the model
and x
i
represents the average number of expected
next events in the replay of the i-th instance. If the
model can always narrow down the expected next
events to just one event, the value of the
appropriateness function is 1.
When checking the conformance of the model
with the instances, we evaluate both the fitness and
appropriateness functions.
4 EXPERIMENT
4.1 Setup
We evaluated our approach using the following
setup. First, we collected job net log data from an
actual SCM system. This system was created by
interconnecting 18 servers fulfilling different roles
such as marketing, production management, and
logistics. Of these 18 servers, we picked out the data
recorded in the five main servers, on which many of
the job nets are executed. For evaluation, we
prepared the two sets of data specified in Table 1:
Log A is data obtained overnight on weekdays in
June and Log B is data obtained for the same days
Table 1: Log data used for experiments.
Duration
Number of
days
Time window
Number of
jobs (avg.)
Log A
2009 June 1st - 30th
(W eekday only)
21 00:0 0 am - 0 6 :00am 1018
Log B
2009 July 1st - 31st
(W eekday only)
23 00:0 0 am - 0 6 :00am 1027
and times in July. Each job’s start/end timestamp is
recorded in the data. In order to evaluate whether
our approach is able to predict the order of job
executions correctly, we constructed the job net
model from Log A and separately checked its
conformance with Log A and with Log B. In
addition, in order to evaluate the effectiveness of our
mining algorithm, we compared the results of our
approach (using all of the steps 1, 2 and 3 in Section
3.2) with the Heuristic Miner Algorithm (using Step
2 only). For the thresholds, we used
1=
p
τ
(sec),
5.0
=
c
τ
, 8.0
=
D
τ
, 1.0
=
R
τ
, and 1.0=
A
τ
.
4.2 Results
We implemented our algorithm in Java and executed
the experiments described in the previous subsection
by using a PC with Windows XP Professional
Edition, 4.3GHz CPU, and 1GB memory. The job
net mining task in each experiment finished within
10 minutes. Since 3,356 individual jobs were
recorded in Log A, the number of events (job start
and end events) in the job net models constructed in
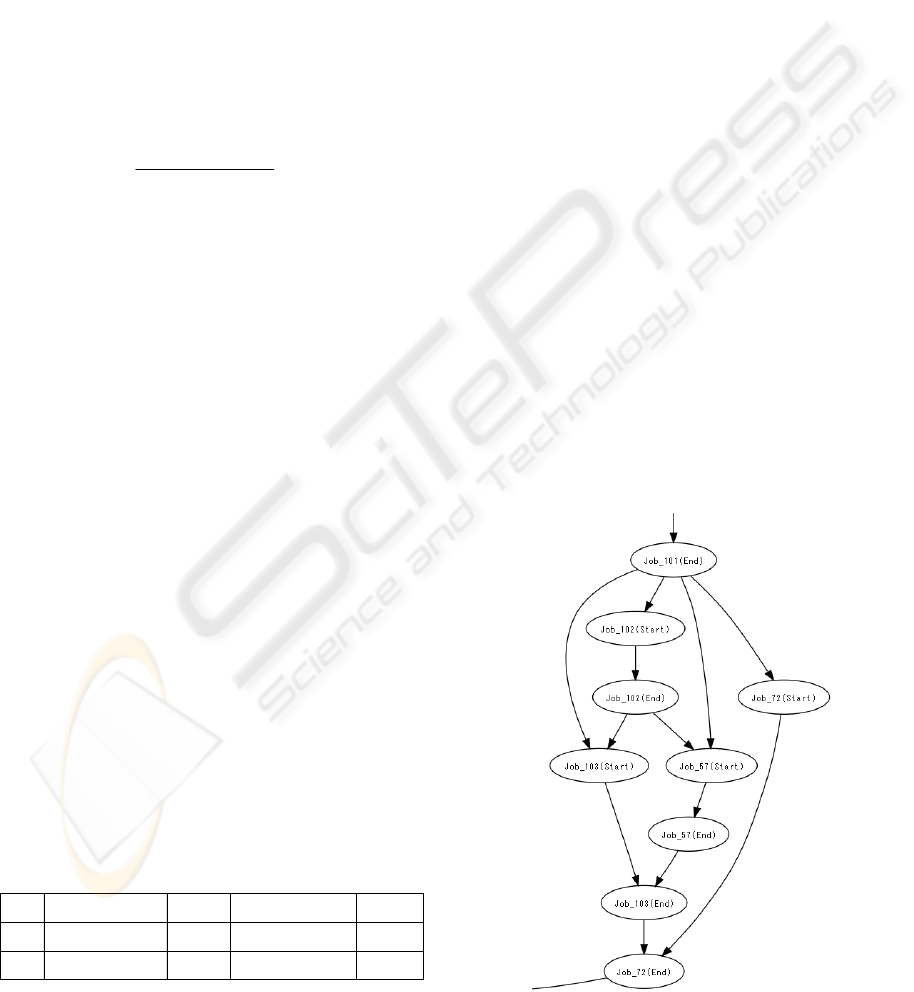
each experiment was 6712. Figure 5 shows a part of
the derived model drawn by Graphviz (Gansner,
2000) with the arrow attributes (AND or XOR)
omitted for simplicity.
Table 2 summarizes the results of the experiments.
Comparing the numbers of unexpected events in
Heuristic Miner (Case 1 and 2) with the numbers in
our approach (Case 3 and 4), it can be seen that the
Figure 5: Job net model (part).
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
10
Table 2: Experimental results.
Case Algorith m
Data
fo r m o d e l
Data for
check
N um ber of
events (avg.)
N um ber of
unexpected
events (avg.)
N um ber of
expected next
events (avg.)
Fitness
A ppropriat
eness
1
H euristic M iner Log A (June) Log A (June)
2035.2 246.4 64.3 0.879 0.991
2
H euristic M iner Log A (June) Log B (July)
2054.7 273.5 64.8 0.867 0.991
3
P roposed algorithm Log A (June) Log A (June)
2035.2 93.7 75.2 0.954 0.989
4
P roposed algorithm Log A (June) Log B (July)
2054.7 122.1 76.4 0.941 0.989
latter are much smaller than the former. This results
in a higher value of fitness parameter for our
approach than for Heuristic Miner. Furthermore, the
numbers of expected next events and the
appropriateness values in both algorithms are almost
the same. Therefore, we can conclude that a more
precise model can be constructed through our
approach than through the Heuristic Miner algorithm
alone, without having much impact on the
appropriateness parameters.
In addition, the difference between the results
produced by the same algorithm (Case 3 and 4) is
quite small. Therefore, we can conclude that our
algorithm is able to predict the behavior of the job
nets in July using the model constructed from the
logs recorded in June with the same precision as in
the case where the log data used for model
construction and for conformance checking are the
same.
5 CONCLUSIONS
We proposed a job net mining method to derive the
execution order of job nets from their logs. In this
method, we identify the set of jobs executed at the
same time. Using this information, we then modify
the job net model derived by the Heuristic Miner
algorithm. Through conformance checking using the
log data of job nets executed in an actual SCM
system, we confirmed that our method enables
construction of a job net model that represents the
order relations between jobs more accurately and
appropriately than that obtained through Heuristics
Miner alone.
We are now considering the following work for
the future. First, we plan to develop methods for the
concise visualization of the structure and
characteristics of job nets. Since it is difficult for
system administrators (humans) to understand the
relationships between over 1000 events in a single
directed graph, we need a method of extracting the
important part of the model or abstracting its
structure in order to make it understandable.
Next, using the proposed approach, we plan to
develop a method of predicting the finishing times
of job nets. Since one of the biggest concerns many
administrators of job nets have is whether or not the
job nets will finish within the deadline, this function
will be able to help them manage their job nets more
efficiently.
Finally, we plan to develop a method for
analyzing the model derived by our approach. For
example, when failures or delays occur in job net
execution, the job representing the root cause can be
detected by backtracking through the order relations
in the derived model. In addition, by measuring the
execution durations of jobs, the critical path, taking
a large amount of time to finish, can be detected.
This information is useful for reorganizing job nets
so as to reduce their execution times. By these
analysis techniques, we will be able to improve
reliability in the management of large scale
integrated complex computer systems.
ACKNOWLEDGEMENTS
We would like to thank Masaru Ito for his help in
collecting job net data and for giving us much useful
advice.
REFERENCES
Fujitsu, 2008, SystemWalker Operation Manager v13.3,
http://www.fujitsu.com/global/services/software/
systemwalker/products/operationmgr/
Van der Aalst, W. M. P., Reijers, H. A., Weijters, A. J. M.
M., van Dongen, B. F., Alves de Medeiros, A. K.,
Song, M., and H. M. W. Verbeek, 2007, Business
Process Mining: An Industrial Application,
Information Systems, 32(5):713-732.
Van der Aalst, W. M. P., Weijters, A. J. M. M., and
Maruster, L., 2004, Workflow Mining: Discovering
Process Models from Event Logs, IEEE Transactions
on Knowledge and Data Engineering, Vol.16, No.9.
Van der Aalst, W. M. P., Alves de Medeiros, A. K.,
Weijters, A. J. M. M., 2005, Genetic process mining,
Proceedings of the 26th international conference on
PROCESS MINING FOR JOB NETS IN INTEGRATED COMPLEX COMPUTER SYSTEMS
11

applications and theory of Petri nets. Lecture notes in
computer science, Vol. 3536. Springer.
Wen L., van der Aalst, W. M. P., Wang, J. and Sun, J.,
2007, Mining process models with non-free-choice
constructs, Data Mining and Knowledge Discovery,
15(2):145-180.
Weijters, A. J. M. M., van der Aalst, W. M. P., and Alves
de Medeiros, A. K., 2006, Process Mining with the
Heuristics Miner-algorithm, BETA Working Paper
Series, WP 166, Eindhoven University of Technology.
Rozinat, A., and van der Aalst, W. M. P., 2008,
Conformance Checking of Processes Based on
Monitoring Real Behavior, Information Systems,
Vol.33, No.1, pp.64-95.
Rozinat, A., and van der Aalst, W. M. P., 2005,
Conformance Testing: Measuring the Fit and
Appropriateness of Event Logs and Process Models,
Proceedings of First International Workshop on
Business Process Intelligence (BPI'05), pp.1-12.
Gansner, E., North, S., 2000, An open graph visualization
system and its applications to software engineering,
Software – Practice & Experience, Vol.30, No.11,
pp.1203-1233.
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
12
