BIO-INSPIRED DATA PLACEMENT IN PEER-TO-PEER
NETWORKS
Benefits of using Multi-agents Systems
Hugo Pommier, Beno
ˆ
ıt Romito and Franc¸ois Bourdon
GREYC - UMR 6072, University of Caen, Bd. du Mar
´
echal Juin, 14032 Caen CEDEX, France
Keywords:
Multi-agents systems, Peer-to-peer, Information placement, Availability, Reliability.
Abstract:
In this paper we present the benefits of using a multi-agents system to manage the data placement in a de-
centralized storage application. In our model, after a fragmentation step, each piece of data is associated to a
mobile agent making its own decisions. To manage agents placement, we apply flocking rules in a peer-to-peer
network called SCAMP. Each agent follows simple rules and the emerging behavior is a flock of fragments.
To provide an efficient load-balancing, agents drop pheromones among network peers. We made some exper-
iments to measure the cohesion degree of our flock and to measure the network coverage of a flock. We also
discuss about availability and reliability of our approach.
1 INTRODUCTION
The data storage in a peer-to-peer network needs an
efficient information scheme. First of all, informa-
tion must be robust and persistent. These properties
might be achieve by using erasure codes. In a such
system, the original data is split into m blocks. Af-
ter an encoding step, m + n fragments are generated.
In this case, the system tolerates n fragment losses.
When using erasure coding, a data can be recon-
structed from any m of the m + n fragments. One of
the most used erasure codes is Reed-Solomon (Plank,
1996). To achieve fault-tolerance and high reliability,
replication might be another solution. However era-
sure codes provides the same level of availability as
replication using less storage cost (Weatherspoon and
Kubiatowicz, 2002).
Reconstruction cost when using erasure codes can
become too heavy in a lot of cases. Hierarchical codes
(Duminuco and Biersack, 2008), a family of erasure
codes, propose a flexible trade-off between classi-
cal erasure codes and replication in terms of perfor-
mances to be used in peer-to-peer storage systems
1
.
The second part of an efficient information
scheme is the fragments placement. The m + n frag-
ments generated by an erasure coding procedure must
1
The fragmentation choice goes beyond the scope of this
study. We only focus on the placement of the information’s
fragments.
be disseminated among peers. The reliability and per-
sistence of information relies on this placement. In
this paper we focus on a new scheme of information
placement based on a MAS (multi-agents system).
Each generated fragment is associated to a mobile
agent making its own decisions. In our approach, the
global information is then seen as a fragments flock
moving into the network.
We also provide load-balancing by using ants stig-
mergy capability. Generated fragments are able to
drop pheromones in the network to establish an in-
direct communication between agents.
After presenting the related work, we present our
architecture composed of two layers. In Section 3.1
we introduce the topology used to scatter our frag-
ments. In Section 3.2 we describe our agents and
their bio-inspired behavior. In Section 4 we present
first results of our approach. Finally we discuss about
security and dependability issues in a system using a
such placement of information.
2 RELATED WORK
Data placement and information availability are hot
topics in the field of peer-to-peer networks. Many
studies (Giroire et al., 2009; Douceur and Watten-
hofer, 2001; Lian et al., 2005) evaluate the cost of
data placement following various criteria (bandwidth,
319
Pommier H., Romito B. and Bourdon F.
BIO-INSPIRED DATA PLACEMENT IN PEER-TO-PEER NETWORKS - Benefits of using Multi-agents Systems.
DOI: 10.5220/0002854703190324
In Proceedings of the 6th International Conference on Web Information Systems and Technology (WEBIST 2010), page
ISBN: 978-989-674-025-2
Copyright
c
 2010 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Mean Time To Data Loss. . . ). We can observe two
main approaches to spread fragments of data in a net-
work. The first one scatters randomly the pieces of in-
formation. The random distribution allows to dissem-
inate fragments on distinct peers with a high proba-
bility in a high scale network. This property limits
the reconstruction cost in terms of bandwidth capac-
ity and the bottleneck effect on one peer. (Kubiatow-
icz et al., 2000) and (Ghemawat et al., 2003) use this
method of dissemination. In (Ghemawat et al., 2003)
a ”master” entity is responsible for data placement
and knows the state of the network but it is not reliable
due to a centralization of the offered service. Another
approach consists to place fragments following the
network topology. An information could be scattered
on all neighbors of a given peer. This method is used
in PAST (Druschel and Rowstron, 2001) and Glacier
(Haeberlen et al., 2005). In this strategy, peers and
data share the same name-space. A peer p is chosen
to be responsible for a given information (generally
the closest id to the data id) and fragments are stored
on neighbors of p. If p fails, the neighboring peers
can participate in data reparation. On the opposite of
a random placement, a fewer distinct peers number
can participate during a reconstruction step. This af-
fects the availability and reliability of data. However
this approach, generally based on top of an overlay us-
ing a Distributed Hash Table (DHT), provides a low
cost scheme of information management in terms of
routing and information placement.
These two methods don’t care about information
environment and its evolution during time. Our model
tries to get advantage of both methods by using a logi-
cal network as a medium for communication between
information fragments. Then we associate to each
data fragment, a mobile agent interacting with its en-
vironment. We manage agent’s movement with flock-
ing rules to keep a local cohesion between them. So
our flock of agents moves randomly in the network,
but the agents keep a high degree of locality.
3 A LAYERED ARCHITECTURE
Our model is built on two layers. The first one is in
charge of the overlay construction. The second one
provides behaviors for our mobile agents.
3.1 Peer-to-peer Network Management
Protocol
The network layer is based on the Scalable Mem-
bership Protocol (SCAMP) (Ganesh et al., 2001;
Ganesh et al., 2003), a fully decentralized peer to peer
lightweight membership protocol. Initially designed
to support reliable gossip-based multicast protocols,
we use it as our network layer for its good properties
in terms of scalability and fault-tolerance to achieve
the required reliability at network level.
In the Erd
˝
os and R
´
enyi (Erd
˝
os and R
´
enyi, 1960;
Erd
˝
os and R
´
enyi, 1959) model, an undirected graph
Γ
n,N
k
is a random graph of n nodes and an average
of N
k
edges if it exists an edge between each pair of
nodes with probability p =
N
k

n
2

. Let P
0
(n,N
k
) denote
the probability of Γ
n,N
k
being completely connected.
Erd
˝
os and R
´
enyi shows that if:
N
k
=
1
2
n log(n) +
1
2
k n (1)
then
lim
n→+∞
P
0
(n,N
k
) = exp
−exp
−k
(2)
which means that if each node of Γ
n,N
k
has a degree of
size log(n)+k then the graph is connected with prob-
ability exp
−exp
−k
. This property is called a connectiv-
ity threshold. If we introduce edges redundancy over
this threshold we achieve fault-tolerance. Results in
(Kermarrec et al., 2003) shows that same threshold
exists for directed random graphs. SCAMP is based
on these results.
SCAMP constructs a random directed graph hav-
ing a mean degree converging to (c + 1)log(n) with c
a design parameter. It permits the graph to stay con-
nected if the link failure probability is smaller than
c
c + 1
(Ganesh et al., 2001). On top of that, the de-
gree size grows slowly with system size so the net-
work scales well in terms of neighborhood size.
3.2 Mobile Agent Layer
In order to propose a new placement of information
scheme in a decentralized storage application, we use
a multi-agents system in which each fragment of in-
formation is kept in an associated cognitive mobile
agent making its own decisions. This cognition al-
lows our agents to autonomously move from peers to
peers following flocking rules.
3.2.1 Flocking Rules
We use flocking rules similar to those proposed by
Craig Reynolds (Reynolds, 1987), inspired by the
movements of birds. His motivation was to find sim-
ple rules, easily applicable to each agent, to reproduce
a flock of birds as an emergent behavior. Reynolds
identified three simple rules for each agent to follow:
WEBIST 2010 - 6th International Conference on Web Information Systems and Technologies
320

• Cohesion: Steer to move toward the average po-
sition of local flockmates.
• Separation: Steer to avoid crowding local flock-
mates.
• Alignment: Steer towards the average heading of
local flockmates.
In this model, flocking is not a quality of any in-
dividual bird but an emergent behavior from interac-
tions between all agents. Our goal is to apply these
rules in a peer-to-peer network. In our case, agents
hold an information fragment, and the resulting emer-
gent behavior is a flock of fragments. Our objective
is to propose a data placement strategy using flocking
rules, in order to combine advantages of global and
local policies. In addition, our approach allows an ef-
ficient load-balancing among peers.
3.2.2 Flocking Algorithm
By combining Reynolds rules with a maximal dis-
tance d between two elements in a network estimated
by the Round Trip Time (RTT), we can reproduce
flocking behavior between fragments. We have de-
fined rules to adapt the flocking model:
1. A given peer can only store one fragment per doc-
ument (separation rule).
2. Agents move in order to get closer to the most
distant agents (cohesion rule associated to a RTT
distance).
3. λ is the maximal distance between two fragments.
Fragments’ positions are given by peer identifiers
storing fragments.
Algorithm 1 allows an agent to move following
flocking rules. This algorithm consists in choosing a
peer from the neighborhood which does not violates
flocking rules.
The first step for a moving fragment is to find
neighboring peers hosting fragments from the same
file. Then, the fragment objective is to get closer to
the most distant peer found. To achieve that, it moves
on a free peer near the distant peer. By applying flock-
ing rules, we can deduce a storage location for a frag-
ment which do not violate the maximal distance be-
tween two fragments.
3.2.3 Load-balancing
In order to propose an efficient load-balancing
scheme, we introduce a pheromone deposit. Our
agents have the capability to interact with the environ-
ment by dropping pheromones. In our case, stigmergy
allows an agent to put a pheromone deposit in the net-
work. So, other agents can detect this trace and then
adapt their storage location. A fragment marks its de-
parture from a peer to another one by a pheromone
deposit on a peer. It also marks its arrival by another
pheromone deposit. So, a given peer in the network
possess a pheromone level for each neighbor. A such
measure is only valid accompanied with an appropri-
ate evaporation rate.
Algorithm 1: Flocking algorithm : moving
from a peer x to a peer p.
Input: A peer x, f ile a file, f
f ile
a fragment
∈ f ile, V
α
peer α’s neighborhood, φ
α
the pheromones level of peer α
Output: A peer p where to store f
f ile
Busy ← peers ∈ V
x
storing fragments ∈ f ile;
foreach y ∈ Busy do
if d(x, y) < λ then
Remove y ∈ Busy
(violation of cohesion rule);
Free ← peers ∈ V
x
storing fragments /∈ f ile;
foreach y ∈ Busy and z ∈ Free and y ∈ V
z
do
if d(y,z) > λ then
Remove z ∈ Free
(application of cohesion rule);
Choose a peer p ∈ F ree such that φ
p
is
minimal;
move f
f ile
to p and increment φ
p
;
4 EXPERIMENTAL RESULTS
We have deployed mobile agents, implemented with
the JavAct
2
framework, in a network built with
SCAMP to measure the size of the flock generated.
We have set the c SCAMP parameter to 3, each agent
drops two units of pheromones for each move, and
the evaporation rate have been set to 0.1% per sec-
ond. We have disseminated flocks of 5, 10, and 20
agents. Figure 1 depicts results with a network build
with 50 computers and figure 2 shows results with a
network of 100 computers. In figure 1 and 2, curves
depict the number of non-isolated agents of a flock
during time. A non-isolated agent is an agent having
at least one fragment in its neighborhood. These re-
sults allows us to validate the behavior of our agents.
In figure 1 flocks of 10 and 20 agents stay grouped
during time. These experiments show that the cohe-
2
http://www.javact.org/
BIO-INSPIRED DATA PLACEMENT IN PEER-TO-PEER NETWORKS - Benefits of using Multi-agents Systems
321

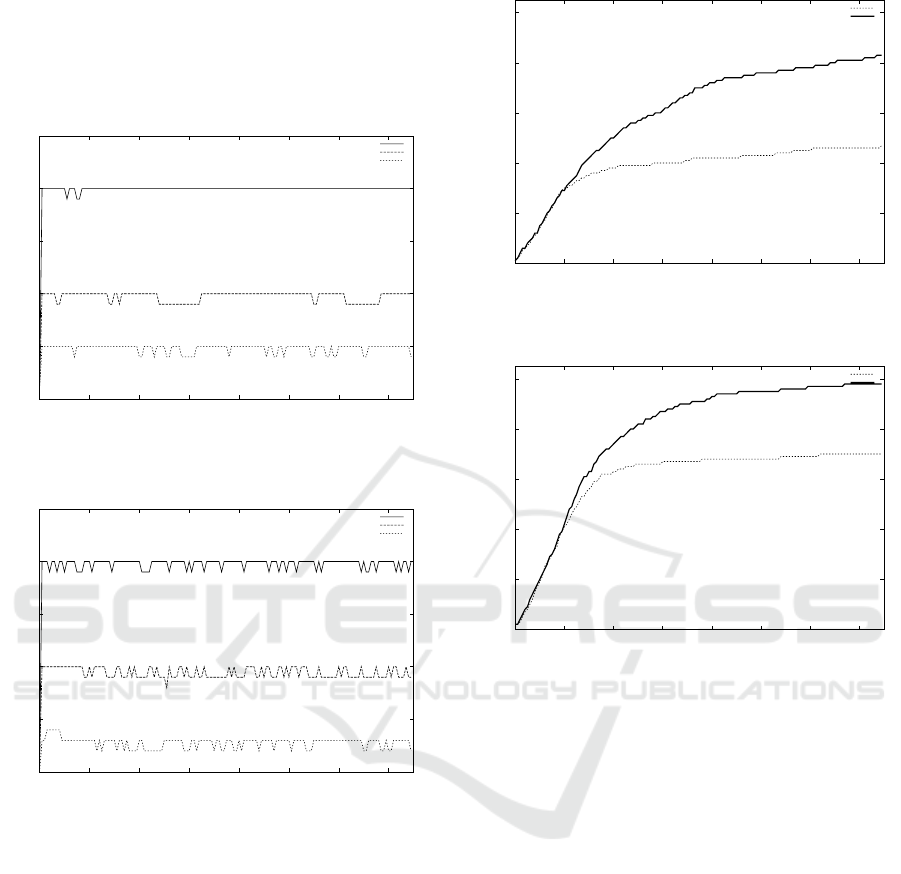
sion of a flock is dependent of the number of agents.
This group behavior is also dependent of the network
configuration. In a small network, small flocks stay
also grouped. So it is necessary to adapt the flock size
to the network size.
0
5
10
15
20
25
0 20 40 60 80 100 120 140
Number of agents
Time (s)
20 agents with pheromones
10 agents with pheromones
5 agents with pheromones
Figure 1: Cohesion of flocks of 5, 10, 15 and 20 agents in a
50 computers network.
0
5
10
15
20
25
0 20 40 60 80 100 120 140
Number of agents
Time (s)
20 agents with pheromones
10 agents with pheromones
5 agents with pheromones
Figure 2: Cohesion of flocks of 5, 10, 15 and 20 agents in a
100 computers network.
We have experimented the network coverage. Fig-
ure 3 and figure 4 show results for 10 and 20 frag-
ments flocks on the same 100 hosts SCAMP net-
work. These curves show the number of visited hosts
during time where each fragment moves every sec-
onds. The dotted curve describes the network cover-
age when pheromones are disabled and the plain one
when they’re not. We clearly see the benefits of using
pheromones during the flocks motions which permits
to cover the quasi totality of this network instance. In
both cases, pheromones usage is helpful to discover
more peers in the network, and thus provides a better
efficiency for the mobility of a flock.
0
20
40
60
80
100
0 20 40 60 80 100 120 140
Network’s average coverage (%)
Time (s)
10 agents without pheromones
10 agents with pheromones
Figure 3: Network’s average coverage by 10 fragments
flocks in a 100 computers network.
0
20
40
60
80
100
0 20 40 60 80 100 120 140
Network’s average coverage (%)
Time (s)
20 agents without pheromones
20 agents with pheromones
Figure 4: Network’s average coverage by 20 fragments
flocks in a 100 computers network.
5 DEPENDABILITY ISSUES OF
THE MULTI-AGENTS
APPROACH
One of the main long-term goals of our approach
is to guaranty the availability of the data stored in
a faulty environment where faults can be correlated.
We define a correlated fault as a fault that is caused
by one another. In a peer-to-peer network, correla-
tions cause multiple nodes to become unavailable at
the same time. This is really problematic if these
nodes stores crucial data. The presence of correlations
comes from shared attributes between the nodes like
their : geographical location, physical network, vul-
nerable services and OS, system administrators, con-
figurations, etc. Those kind of faults are not negligi-
ble (Bakkaloglu et al., 2002) and should be consid-
ered. However, some studies (Weatherspoon and Ku-
biatowicz, 2002; Lin et al., 2004) uses the indepen-
dence hypothesis in their analysis due to the hardness
of taking the correlations into account.
WEBIST 2010 - 6th International Conference on Web Information Systems and Technologies
322

A first idea to solve this problem is developed in
Glacier (Haeberlen et al., 2005), a decentralized stor-
age system. Glacier makes heavy use of erasure cod-
ing techniques coupled with a repair mechanism in
case of failure to ensure the required availability level
even if the system is severely damaged. However, the
fragments placement made by Glacier is key-based
and static into a DHT. As a consequence, an attacker
knowing the fragments’ keys could target their host-
ing nodes to make the data unrecoverable.
A second idea proposed in the literature is to cre-
ate a correlated faults model (Weatherspoon et al.,
2002; Bakkaloglu et al., 2002) from various obser-
vations of the overlay. The model is then used to cre-
ate clusters of correlated nodes. The idea is to adopt a
proactive approach in distributing a maximum of frag-
ments on different clusters to prevent the loss of mul-
tiple fragments after a fault.
From these observations, we propose a flexible ap-
proach to avoid the static key-based placement with-
out losing the ability to self-repair during the flock
lifetime. Our goal is to combine the massive fragmen-
tation approaches with proactive mobile-based ap-
proaches to solve the problem of the availability of
data in presence of correlated failures. More precisely
we think that:
1. In our architecture, each flock knows its compo-
sition (the number and the location of fragments)
and the environment it explores (the peers it dis-
covers), making it able to plan a repair when its
size has reached a given critical threshold. In
case of hierarchical codes (Duminuco and Bier-
sack, 2008) for example, the system can com-
pute P( f ailure|a), the probability of complete
data loss if other a fragments loses occur.
2. The second interest of a mobile-agents based ap-
proach is the faculty for the flock to change it’s
location when the environment evolves. If we
suppose a correlated faults model of the network,
the flock can search an optimal placement during
its motion which minimizes the inter-correlation
between its hosting nodes using techniques like
simulated-annealing. Since we are in a dynamic
environment, the flock searches a new optimal po-
sition every time the equilibrium is disturbed (typ-
ically after a fault or a node join into the neighbor-
hood of the flock).
3. In opposition with Glacier where an attacker
knowing the fragments’ keys could provoke an
unrecoverable failure, the flock’s location is not
accessible to attackers and its motion is quite un-
predictable making the setup of these kind of at-
tacks very difficult.
6 CONCLUSIONS
We presented in this paper the bases of a new ap-
proach to handle the problems of data placement and
its dependability in decentralized data storage sys-
tems. The described approach claims to be flexi-
ble and adaptable by using mobile agents moving in
flocks in a peer-to-peer network. Our experimenta-
tions show that cohesion of the flock is preserved dur-
ing its motion. However, this cohesion is dependent
of the network size and consequently of the number
of neighbors per peer. This is clearly a SCAMP re-
lated constraint where the neighborhood grows with
the network size. The pheromones deposit guaranties
that almost all network nodes are visited after sev-
eral flock motions. Those experimentations validate
to some extent our approach basis.
The next step of our work aims to make good use
of the flock’s knowledge and its environment to pro-
pose a proactive and optimal data placement guaran-
tying the required dependability level in presence of
correlated faults. Finally, we will measure the costs
of our approach in comparison to existing locals and
random data placements.
REFERENCES
Bakkaloglu, M., Wylie, J. J., Wang, C., and Ganger, G. R.
(2002). On correlated failures in survivable stor-
age systems. Technical Report CMU-CS-02-129,
Carnegie Mellon University.
Douceur, J. and Wattenhofer, R. (2001). Competitive hill-
climbing strategies for replica placement in a dis-
tributed file system. In Proceedings of the 15th Inter-
national Conference on Distributed Computing, pages
48–62, London, UK. Springer-Verlag.
Druschel, P. and Rowstron, A. (2001). PAST: A large-scale,
persistent peer-to-peer storage utility. Workshop on
Hot Topics in Operating Systems, pages 75–80.
Duminuco, A. and Biersack, E. (2008). Hierarchical codes:
How to make erasure codes attractive for peer-to-peer
storage systems. IEEE International Conference on
Peer-to-Peer Computing, pages 89–98.
Erd
˝
os, P. and R
´
enyi, A. (1959). On random graphs. I.
In Publicationes Mathematicae Debrecen, pages 290–
297.
Erd
˝
os, P. and R
´
enyi, A. (1960). On the evolution of random
graphs. In Publications of the Mathematical Institute
of the Hungarian Academy of Sciences, pages 17–61.
Ganesh, A. J., Kermarrec, A.-M., and Massouli
´
e, L. (2001).
Scamp: Peer-to-peer lightweight membership service
for large-scale group communication. In Proceedings
of the 3rd International Workshop Networked Group
Communication, pages 44–55, London, UK.
BIO-INSPIRED DATA PLACEMENT IN PEER-TO-PEER NETWORKS - Benefits of using Multi-agents Systems
323

Ganesh, A. J., Kermarrec, A.-M., and Massouli
´
e, L. (2003).
Peer-to-peer membership management for gossip-
based protocols. IEEE Transactions on Computers,
52(2):139–149.
Ghemawat, S., Gobioffd, H., and Leung, S.-T. (2003). The
google file system. In Proceedings of the 19th ACM
Symposium on Operating Systems Principles, pages
29–43, New York, NY, USA.
Giroire, F., Monteiro, J., and P
´
erennes, S. (2009). P2P stor-
age systems: How much locality can they tolerate? In
Proceedings of the 34th IEEE Conference on Local
Computer Networks (LCN), pages 320–323.
Haeberlen, A., Mislove, A., and Druschel, P. (2005).
Glacier: highly durable, decentralized storage despite
massive correlated failures. In Proceedings of the
2nd conference on Symposium on Networked Systems
Design & Implementation, pages 143–158, Berkeley,
CA, USA. USENIX Association.
Kermarrec, A.-M., Massouli
´
e, L., and Ganesh, A. J. (2003).
Probabilistic reliable dissemination in large-scale sys-
tems. IEEE Transactions on Parallel and Distributed
Systems, 14(3):248–258.
Kubiatowicz, J., Bindel, D., Chen, Y., Czerwinski, S.,
Eaton, P., Geels, D., Gummadi, R., Rhea, S., Weath-
erspoon, H., Weimer, W., Wells, C., and Zhao, B.
(2000). Oceanstore: an architecture for global-
scale persistent storage. ACM SIGPLAN Notices,
35(11):190–201.
Lian, Q., Chen, W., and Zhang, Z. (2005). On the impact
of replica placement to the reliability of distributed
brick storage systems. In Proceedings of the 25th
IEEE International Conference on Distributed Com-
puting Systems, pages 187–196, Washington, DC,
USA. IEEE Computer Society.
Lin, W. K., Chiu, D. M., and Lee, Y. B. (2004). Erasure
code replication revisited. In Proceedings of the 4th
International Conference on Peer-to-Peer Computing,
pages 90–97, Washington, DC, USA. IEEE Computer
Society.
Plank, J. S. (1996). A tutorial on reed-solomon coding for
fault-tolerance in raid-like systems. Technical Report
CS-96-332, University of Tennessee.
Reynolds, C. W. (1987). Flocks, herds and schools: A dis-
tributed behavioral model. In Proceedings of the 14th
annual conference on Computer graphics and inter-
active techniques, pages 25–34. ACM.
Weatherspoon, H. and Kubiatowicz, J. (2002). Erasure cod-
ing vs. replication: A quantitative comparison. In Pro-
ceedings of the 1st International Workshop on Peer-to-
Peer Systems, pages 328–338, London, UK. Springer-
Verlag.
Weatherspoon, H., Moscovitz, T., and Kubiatowicz, J.
(2002). Introspective failure analysis: Avoiding corre-
lated failures in peer-to-peer systems. In Proceedings
of the 21st Symposium on Reliable Distributed Sys-
tems, pages 362–367, Los Alamitos, CA, USA. IEEE
Computer Society.
WEBIST 2010 - 6th International Conference on Web Information Systems and Technologies
324