IMPLEMENTING DYNAMIC-EPISTEMIC QUESTIONING
Engineering and Teaching Information Seeking via Dynamic Inquiry
S¸tefan Minic
˘
a
Institute for Logic, Language and Computation, University of Amsterdam, Science Park 904, Amsterdam, Netherlands
Keywords:
Logic Education, Computer Supported Learning, Information Dynamics, Question, Inquiry, Epistemic Games.
Abstract:
Asking questions in multi-agent environments is an interesting and complex phenomenon with potential ap-
plications for both education and information technologies. We approach the problem of building an adequate
model for questioning phenomena using dynamic-epistemic formalism and we present an implementation
of multi-agent dynamic-epistemic questioning using Haskell. We start by introducing a dynamic-epistemic
logic for questions which extends previous results from (van Benthem and Minic
˘
a, 2009). Next, an imple-
mentation for model-checking in epistemic-issue models is proposed based on a similar implementation for
epistemic logic from (van Eijck, 2004). We conclude the paper by probing potential applications of this results
in education and beyond by presenting an ongoing project of building an accessible and intuitive web-based
graphical interface to be used in an electronic teaching environment for visualizing, designing and managing
strategies for asking questions during abstract scientific inquiry and in cooperative or competitive scenarios of
multi-agent goal-driven investigations and interrogative interactions.
1 INTRODUCTION
Questions are important for various reasons. Under-
standing their abstract structure is considered to be a
significant problem in various fields of research. In
information theory and AI, a formal model of ques-
tions is important for achieving the goal of imple-
menting question-asking machines (Knuth, 2005). In
logic, semantics and pragmatics of natural language
the aim is to understand questioning by human users
(Wi
´
sniewski, 1996; Groenendijk, 2008; Ciardelli and
Roelofsen, 2009). In epistemology and philosophy of
science questions are studied because of their role in
belief revision mechanisms (Baltag and Smets, 2008;
Enqvist, 2009) and in interrogative processes of sci-
entific inquiry (Hintikka et al., 2002; Genot, 2009). A
dynamic epistemic approach to questions makes the
interaction between questioning actions and knowl-
edge explicit and shows how information changing
events are relevant for a large variety of rational activ-
ities ranging from multi-agent interaction to scientific
inquiry (Baltag, 2001; Unger and Giorgolo, 2008; van
Benthem and Minic
˘
a, 2009; Icard, 2009; Peli
ˇ
s, 2009).
2 QUESTIONING THEORY
This section presents problems and methods regard-
ing modeling of questioning phenomena from a theo-
retical perspective. It will introduce a Dynamic Epis-
temic Logic of Questions (henceforth, DELQ) which
adds some innovative features to contributions from
(van Benthem and Minic
˘
a, 2009).
The formal language used to describe questioning
actions is given by the following BNF:
ϕ ::= ⊥ | p | i | ¬ϕ | (ϕ ∧ ψ) | 
G
ϕ | [
~
ϕ?]
H
ψ | [!]
H
ϕ
where p is a propositional symbol, i is a nominal sym-
bol,  ∈ {K,R, Q,C}, an agent group G is a set of
agent labels, singletons if  6= C,
~
ϕ = hϕ
0
,. .. , ϕ
n
i is
a vector of formulae, and H = h
~
G
0
,. .. ,
~
G
n
i is a vector
of vectors containing groups of agents.
DELQ formulae are interpreted in Epistemic Issue
Models (henceforth, EIM). EIMs are standard rela-
tional structures defined as tuples M = hW,
a
∼,
a
≈,V, Ni
where W
M
is a set of epistemic alternatives,
a
∼
M
is a
family of equivalence relations on W
M
representing
epistemic indistinguishability,
a
≈
M
is a family of bi-
nary relations, one for each agent a ∈ A, represent-
ing issue-equivalence, V
M
: P → ℘(W
M
) is a standard
367
Minic
ˇ
a ¸S. (2010).
IMPLEMENTING DYNAMIC-EPISTEMIC QUESTIONING - Engineering and Teaching Information Seeking via Dynamic Inquiry.
In Proceedings of the 2nd International Conference on Computer Supported Education, pages 367-372
DOI: 10.5220/0002857703670372
Copyright
c
 SciTePress

propositional valuation function, and N
M
: N → W is
a naming function, for any given mutually disjoint
countable sets P, N, A of propositional atoms, name
symbols, and agent labels, respectively.
The interpretation of DELQ formulae is given re-
cursively at a world w in an EIM by this clauses:
M |=
w
⊥ iff w ∈ ∅
M |=
w
p iff w ∈ V (p)
M |=
w
i iff w ∈ N(i)
M |=
w
¬ϕ iff not M |=
w
ϕ
M |=
w
ϕ ∧ ψ iff M |=
w
ϕ and M |=
w
ψ
M |=
w

G
ϕ iff ∀v : w ↔ v ⇒ M |=
v
ϕ
M |=
w
[α]
H
ϕ iff M ⊗ E |=
Z
M⊗E
(w)
ϕ
where: ↔=









(
a
∼)
a∈G
if  = K,
(
a
≈)
a∈G
if  = Q,
(
a
∼ ∩
a
≈)
a∈G
if  = R,
(
S
a∈G
a
∼)
∗
otherwise
and M ⊗ E = hW
M⊗E
,
a
∼
M⊗E
,
a
≈
M⊗E
,X
M⊗E
,Z
M⊗E
i is
the EIM obtained via the product update mechanism
given below for any Epistemic Questioning Action
Model (henceforth, EQAM) E = hS,
a
∼,
a
≈,X, Zi such
that, for any questioning action [α]
H
and EIM M:
S =

S
ϕ
i
∈
~
ϕ
{ϕ
i
,ϕ
i
,{ϕ
i
,ϕ
i
}} if α =
~
ϕ?,
{e | e = N
M
(w),w ∈ W
M
} otherwise
a
∼=

{(e,e
0
) | ∃s,s
0
: e ∈ s ∧ e
0
∈ s
0
} if α =
~
ϕ?,
{(e,e
0
) | N
−1
M
(e)
a
≈ N
−1
M
(e
0
)} otherwise
a
≈=

{(ϕ
i
,ϕ
i
) | ϕ
i
∈
~
ϕ,a 6∈
~
G
i
(2)} if α =
~
ϕ?,
{(e,e
0
) | e ∈ S,e
0
∈ S} otherwise
X(e) =

prq(e) if α =
~
ϕ?,
exe(e) otherwise
Z(e) =

str(e) if α =
~
ϕ?,
e
a
! otherwise
with prq : S →℘(W
M
), exe : S →℘(W
M
) given by:
prq(e) =

JeK
M
if e ∈ {ϕ,
ϕ} for some ϕ ∈
~
ϕ,
Jh(e)K
M
if e = {ϕ,ϕ} for some ϕ ∈
~
ϕ
where, for every ϕ
i
∈
~
ϕ and
~
G
i
∈ H, h({ϕ
i
,
ϕ
i
}) =
^
a∈G
i
(0)
(¬(K
a
ϕ
i
∨ K
a
¬ϕ
i
) ∧
b
K
a
_
b∈G
i
(1)
(K
b
ϕ ∨ K
b
¬ϕ))
exe(e) = {w | N
−1
M⊗E
(N
M
(w)
a
!)
A
∼ x, x ∈ W
∗
M⊗E
}
where W
∗
M⊗E
⊆ W
M⊗E
, and
A
∼ = (
a
∼)
a∈A
.
1
Given an EIM M = (hW,
a
∼,
a
≈,V i,W
∗
) together
with a designated set of worlds W
∗
⊆ W, an EQAM
1
Conditions for executing both questioning and resolu-
tion actions can be different in a variety of specific contexts.
E = hS,
a
∼,
a
≈,X, Zi, the product update model M ⊗E
is defined as M
⊗
= (hW
⊗
,
a
∼
⊗
,
a
≈
⊗
,V
⊗
,N
⊗
i,W
∗
⊗
) with:
W
⊗
= {(w, e) | w ∈ W,e ∈ S},
N
⊗
= {n
a
e | (N
−1
(n),Z(e)) ∈ W
⊗
},
V
⊗
(p) = {(w,e) | w ∈ V (p),e ∈ S},
N
⊗
(m) = {(V (n), Z
−1
(e)) | n
a
e = m},
a
∼
⊗
= {((w, e), (w
0
,e
0
)) | w ∈ X(e,e
0
) ⇔ w
0
∈ X(e,e
0
),
w ∈ X(e) ⇔ w
0
∈ X(e
0
),w
a
∼ w
0
,e
a
∼ e
0
},
a
≈
⊗
= {((w, e), (w
0
,e
0
)) | w
a
≈ w
0
,e
a
≈ e
0
},
W
∗
⊗
= {(w, e) | w ∈ W
∗
,e ∈ E}.
Figure 1 gives an intuitive illustration of the way
this mechanism works for a concrete example.
pq
∗
pq pq
a b
pq
∗
6|= K
a
(p ∧ q) ∨ K
a
(p ∧ q)
pq
∗
|=
b
K
a
(K
b
(p ∧ q) ∨ K
b
p ∧ q)
pq |=
b
K
a
(K
b
(p ∧ q) ∨ K
b
p ∧ q)
pq 6|=
b
K
a
(K
b
(p ∧ q) ∨ K
b
p ∧ q)
⊗
[p ∧ q]?
[a,b,∅]
p ∧ q
p ∧ q

p ∧ q
p ∧ q

ab
pre(p ∧ q) = {pq
∗
}
pre(p ∧ q) = {pq, pq}
pre({p ∧ q, p ∧ q}) = {pq, pq
∗
}
⇓
pq
a
{p ∧ q, p ∧ q}
pq
a
p ∧ q pq
a
p ∧ q
pq
a
p ∧ q
pq
a
{p ∧ q, p ∧ q}
pq
a
p ∧ q
pq
a
∗
p ∧ q pq
a
∗
p ∧ q
pq
a
∗
{p ∧ q, p ∧ q}
ab
ab
a a
a
Figure 1: Product update for multi-agent questions.
CSEDU 2010 - 2nd International Conference on Computer Supported Education
368

3 IMPLEMENTATION
This section presents an implementation for DELQ
using Haskell. It will describe an Haskell program
implementing model-checking for DELQ based on
an already existing Haskell implementation for multi-
agent Dynamic Epistemic Logic (henceforth, DEL)
called Dynamic Epistemic MOdeling (henceforth,
DEMO) developed in (van Eijck, 2004).
The Haskell implementation for the theory intro-
duced in the previous section proceeds along the ex-
pected lines. Even though some design choices and
a number of coding details are noteworthy the imple-
mentation is, essentially, a translation from the previ-
ous notation into Haskell functions and datatype defi-
nitions. We refrain from listing all the code lines and
will focus on presenting a selection of main features.
We start by implementing a data structure for the
formulae in the static fragment of our language:
data Formq = Top | Prop Prop | Neg Formq
| Conj [Formq] | Disj [Formq]|K Agent Formq
| X Agent Formq | O Agent Formq
| CK [Agent] Formq |W Formq deriving (Eq,Ord)
EIMs are represented by the following data structure:
data QEM state = Qm [state] [Agent]
[(Agent,state,state)] [(Agent,state,state)]
[(state,[Prop])] [(state,String)]
[state] deriving (Eq,Show)
The function isTrueAt gives the interpretation of the
language in a relational structure. It is defined as:
trueAt :: ( Ord state ) =>
QEM state -> state -> Formq -> Bool
trueAt m w Top = True
trueAt m@(Qm _ _ _ _ vl _ _) w (Prop p)=
elem p (concat [props|(w’,props)<-vl,w’== w])
trueAt m w (Neg f) = not (isTrueAt m w f)
trueAt m w (Conj fs) = and (map (trueAt m w) fs)
trueAt m w (Disj fs) = or (map (trueAt m w) fs)
trueAt m@(Qm _ _ acc _ _ _ _) w (K agt f) =
and(map(flip (trueAt m) f)(rightS (rlk agt m) w))
trueAt m@(Qm _ _ acc eqq _ _ _) w (X agt f) =
and(map(flip (trueAt m) f)(rightS (rlx agt m) w))
trueAt m@(Qm _ _ _ eqq _ _ _) w (O agt f) =
and(map(flip (trueAt m) f)(rightS (rlq agt m) w))
trueAt m@(Qm dom ags acc _ _ _ _) w (CK agts f)=
and(map(flip (trueAt m) f)(comAlts ac agts dm w))
trueAt m w (W f) = True
We use a similar data structure to represent EQAMs:
data QAM act = Qa [act] [Agent]
[(Agent,act,act)] [(Agent,act,act)]
[(act,[Int])] [(String,act)] deriving(Eq,Show)
To make some computations easier we store both
epistemic events and their names in EQAM states:
type State = (Formq, String)
type Quac = ([Formq], Hrup)
type Hrup = [[[Agent]]]
Questioning actions are then pairs of lists of formulae
and lists of agents that are relevant for the action. The
following definition provides the construction of a re-
lational structure that represents a questioning action:
quac :: (Show state, Eq state) =>
QEM state -> Quac -> QAM State
quac m@(Qm dom ags acc eqq val nam act) qk =
(Qa dom’ ags’ acc’ eqq’ pex nam’)
where
dom’ = fdom m qk
ags’ = ags
acc’ = fsim m qk
eqq’ = fapr m qk
pex = fxpr m qk
nam’ = fnam m qk
EQAM components are constructed by auxiliary
functions using as input EIMs and a questioning acts:
fdom :: (Show state) =>
QEM state -> Quac -> [State]
fdom m@(Qm dom _ _ _ _ _ _) qk
| fst qk == [W Top] = zip (map (\x->Top)
[1..(length dom)]) (map show dom)
| otherwise = (zip (fst qk) (map show
(fst qk))) ++ (zip (map Neg (fst qk))
(map show (map Neg (fst qk)))) ++
(zip (map W (fst qk)) (map show
(map W (fst qk))))
We only give here for illustration the code of the func-
tions computing two of the components of an EQAM:
fsim :: (Show state, Eq state) =>
QEM state->Quac->[(Agent, State, State)]
fsim m@(Qm _ ags acc eqq _ _ _) qk
| fst qk == [W Top] = [(x,y,z) |
x<-ags, y<-(fdom m qk), z<-(fdom m qk),
(x,(who m (snd y)),(who m (snd z)))‘elem‘eqq]
| otherwise = [(x,y,z) | x <- ags,
y<-(fdom m qk),z<-(fdom m qk),(not(’?’ ‘elem‘
(show(fst y)))),(not(’?’‘elem‘(show(fst z))))]
ab
ab
ab
ab
ab
ab
ab
ab
ab
3:[p,q]
2:[p]
a
1:[q]
b
0:[]
b
a
3:[p,q;p]
2:[p;p]
a
1:[q;~ p]
b
0:[;~p]
b
a
3:[p,q;q]
2:[p;~ q]
a
1:[q;q]
b
0:[;~q]
b
a
3:[p,q;pq]
2:[p;p~ q]
a
1:[q;~ pq]
b
0:[;~p~ q]
b
a
Figure 2: Example of EIMs before and after an updated with
one or two questions in Graphviz generated format.
IMPLEMENTING DYNAMIC-EPISTEMIC QUESTIONING - Engineering and Teaching Information Seeking via
Dynamic Inquiry
369

We supplement these abstract definitions by an in-
tuitive illustration in Graphviz output before a resolu-
tion action is performed, see Figure 2.
The remaining functions implement the product
update rule in a way that goes along the implemen-
tation for the standard product update rule for infor-
mative actions from DEMO (van Eijck, 2004). Most
of the details are standard in DEL and we will skip
them here, there are also some specific details that dif-
fer when questioning actions are considered. Some of
the aspects that emerge when interrogative events are
introduced are studied in (Baltag, 2001). Some other
aspects are even more problematic both conceptually
and technically when multiple questions are consid-
ered, in particular, there is no composition principle
for questions and for complex questioning actions se-
quential or parallel execution lead to different out-
comes. We do not pursue this direction here, a more
detailed discussion of these and other related aspects
can be found in (van Benthem and Minic
˘
a, 2009).
4 APPLICATIONS
This section explores possible applications of results
in previous section. We describe first applications in
teaching and computer supported education and we
also mention some further theoretical developments
towards the end of the section.
A first possible application concerns the role of
question-management actions in interactive educa-
tion. We present ongoing work towards building a
web application with a user-friendly graphical inter-
face linked with Haskell and Graphviz server based
programs in order to produce interactive and intu-
itive visual representations (SVG output) for compu-
tations using questioning actions that are changing
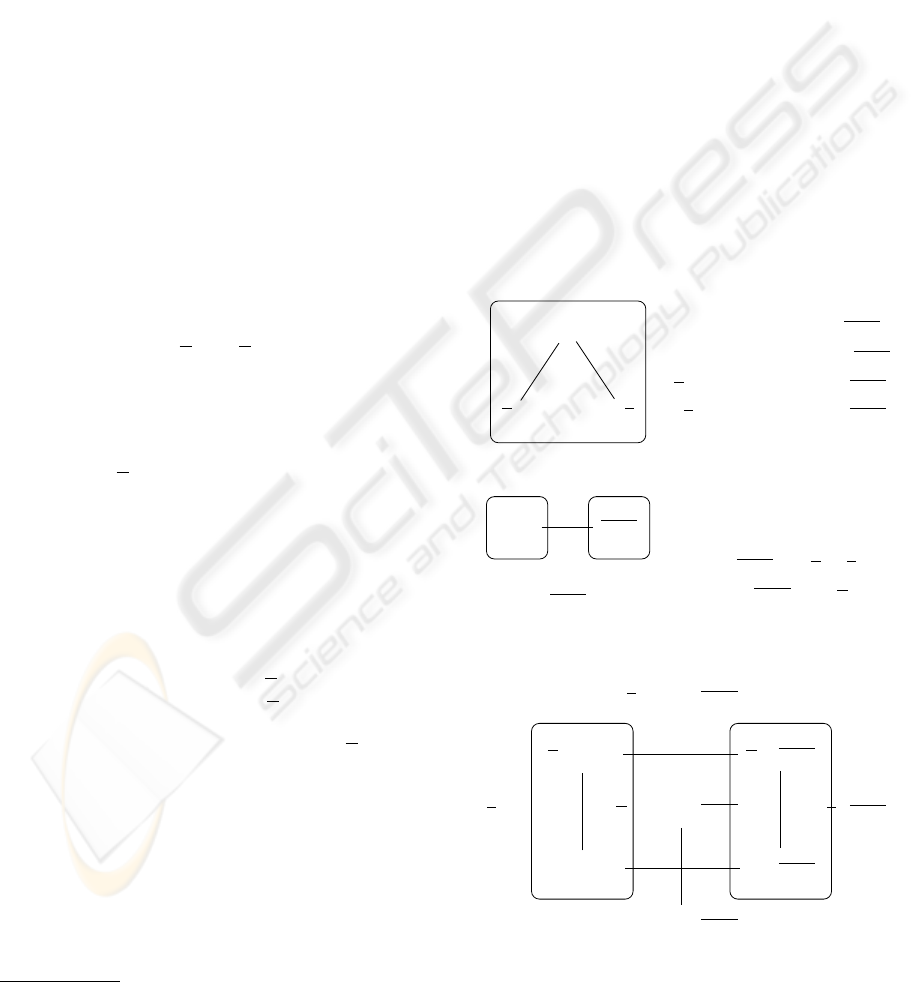
epistemic-issue structures. The workflow diagram for
this application is given in Figure 3. In what follows
we will describe empirical data about the application
as it is at this stage of development. Another possible
application, interdependent on the first, is design and
management of questioning strategies.
The first direction in which we intent to con-
tinue and develop results form previous sections is an
immediate application inside an teaching-supporting
electronic environment. We are aware of previous re-
search in this direction that make the case for the ad-
vantages of having such teaching tools for a variety
of domains and subjects. There is no reason to be-
lieve that the specific domain of logic for interactive
interrogative actions is an exception from this point of
view. Moreover, a suitable teaching environment for
both interactive questioning and abstract issue man-
agement has the potential of producing useful appli-
cations in many other scientific domains. As long as
recurrent interrogative structures are engaged in a spe-
cific field of study, there is good evidence to believe
that a dynamic approach to questioning might be use-
ful for identifying and understanding such patterns.
Some specific aspects of DELQ could make this
task maybe more challenging. For instance, by the
very fact that reasoning about epistemic and interrog-
ative realities is done inside relational structures, an
effective educational environment would have to pro-
vide feedback in both text messages and formulae de-
scribing computations and a more demanding graphi-
cal format. This is still an emerging practice but basic
teaching experience seems to indicate that any type
of feedback that would be relevant and efficient for
teaching purposes should at least contain basic visu-
alizations and processing of graph structures.
Besides allowing to perform model checking in
epistemic structures, DEMO is also designed for pro-
ducing output describing epistemic content of rela-
tional structures in a format that can be graphically
displayed and used to enhance intuitively thrusted
computations about interesting phenomena involving
knowledge and interactive information flow. Given
their very similar relational structure, it is reasonable
to expect that EIM’s are also suitable candidates for
a similar approach. There are also software solutions
that support web-based viewers for Graphviz output.
WebDot is such an example of a scripted service that
could be used for visualizing graphs in HTML docu-
ments to be used as teaching tools.
More concretely, one specific feature of DEMO
is the fact that it can output epistemic models in
Graphviz format. Nodes of the graph represent possi-
ble worlds, edges between nodes represent indistin-
guishability relations, information about the agents
and the valuation is represented by labels on edges
and worlds. For our present purpose, because the
issue relation, used to represend questions, is also
an equivalence relation as is the epistemic indistin-
guishability relation, a representation of both as links
between nodes becomes problematic. In order to re-
flect the conceptual difference between them we de-
cided to use clustering of nodes for questions and
edges for knowledge.
In order to obtain output in the previously spec-
ified graphical format we use the fdp layout pro-
gram. Equivalence classes formed by issue relations
are grouped in one cluster and labels are used to repre-
sent the agents. Figure 2 representa an EIM in which
two agents a and b are ignorant about two proposi-
tions p and q. The initial frame, including all the al-
ternatives, represents a universal issue relation. Ask-
CSEDU 2010 - 2nd International Conference on Computer Supported Education
370

ing a question (in this example p? or q?) splits the
domain in two partition cell, represented here as clus-
ters. Asking two questions in parallel splits the do-
main in four clusters at once.
At the moment all these are still under develop-
ment and there are many aspects that can be im-
proved. We mention some directions for future de-
velopment in comparison to other existing established
approches in the next section. Interliked with these
we mention here some more theoretical aspects that
could be attached once such a software architecture is
in place. Its functionality could easily be expanded
in other relevant directions in close interaction and by
incorporating input from other related topics that are
studied in DEL. Questioning actions are even more
relevant in strategic interactions and over structured
sequences or long-term processes of inquiry. Results
and techniques used in studies of multi-agent strategic
interaction in an epistemic framework such as pub-
lic announcement games from (
˚
Agotnes and van Dit-
marsch, 2009) could be extended to include question-
ing actions and further enrich the present approach.
It is also often the case that the real practice of in-
quiry and scientific investigation also shows that there
are various aspects that lead to various restrictions
with regard to which kind of questioning actions are
available in a certain context. Experimental designs
come with complex patterns of dependence between
what, how, and when is available for investigation.
(van Benthem et al., 2009) introduces protocols to
study information flow during structured sequences
of epistemic actions. Such techniques are also rel-
evant for questioning actions and could be used to
study long-term design and management of question-
ing strategies in scientific inquiry.
Client Server
User Input (text)
Haskell (demo)
EIMs update
Text + Dot
Graphviz (fdp)
SV G format
Figure 3: Workflow diagram for DELQ update.
5 COMPARISONS
There already exist previous software architectures
that have both a web-based accessible and intuitive
user interface and interactive feedback provided by a
Haskell program running on a remote server to the
student performing derivations in order to solve a spe-
cific exercise. (Gerdes et al., 2008) gives an expo-
sition of such such a successful project. It uses a
web-based user-friendly interface that communicates,
using an Ajax-based solution, with Haskell functions
computing next steps in derivations and giving feed-
back about strategic applications of rules in further
steps in the form of text messages. Strategic feedback
is also provided about which next steps are better in
a specific exercise. Our approach does not include
strategic feedback but such a feature is a desideratum
for future development.
We are also aware of other possibilities for a suit-
able framework providing users access to computing
operations on relational structures in a visual graphi-
cal format. One such example of an existing software
solution that is easily available and might be also rel-
evant in our context is SAGE. It is an open source
software used for visualizing algebraic and geomet-
ric structures, its main features are described in (Stein
and Joyner, 2005).
While previously mentioned approaches focus on
algebraic structure of graphs in our approach rela-
tional structures are used as support for intensional
reasoning using modal logic. There exist also previ-
ous approaches implementing reasoning with modal
logic. LoTREC is such an example of a generic
tableau-based theorem prover for intensional reason-
ing (Farias del Cerro et al., 2001). Compared with this
our approach fosuses more on model checking tasks.
But there exists an underlying calculs of issues and
knowledge that could serve as a basis for adding va-
lidity testing and other syntactic functionality to our
approach. On the other hand, the graphical represen-
tation of relational structures could be easily used as
teaching aid for other related logical task.
6 CONCLUSIONS
We have presented a theoretical approach to question-
ing that builds on previous results in the field and in-
troduces some innovative features in DELQ.
We have shown how these new features can be im-
plemented in a Haskell program by extending previ-
ous implementations of similar aspects in DEMO.
We have presented ongoing work on a project
of developing an educational electronic environment
IMPLEMENTING DYNAMIC-EPISTEMIC QUESTIONING - Engineering and Teaching Information Seeking via
Dynamic Inquiry
371

that makes use of these results. Various possible solu-
tions available for similar problems have been consid-
ered and their relevance for questioning actions have
been assessed. Some of the difficulties and challenges
for fulfilling such a project have also been considered.
Based on all these aspects we have argued for the
potential benefits of a software architecture used for
modeling questioning actions and visualizing epis-
temic issue structures in an electronic environment.
We have found good reasons to believe that such a so-
lution is very relevant and useful for educational pur-
poses and could be used for teaching and enhancing
important questioning skills.
We have also made a case for potential further
extensions towards using our framework in under-
standing theoretical aspects, building practical skills
and enhancing cognitive abilities, involved in strate-
gic design and long-term management of questioning
in multi-agent interaction or scientific investigation.
REFERENCES
˚
Agotnes, T. and van Ditmarsch, H. (2009). What will they
say? - public announcement games. In Proc. of Logic,
Game Theory and Social Choice 6. Tsukuba, Japan.
Baltag, A. (2001). Logics for insecure communication. In
Proc. of TARK’01. Morgan Kaufmann.
Baltag, A. and Smets, S. (2008). A qualitative theory of
dynamic interactive belief revision. Texts in logic and
games, 3:9–58.
Ciardelli, I. and Roelofsen, F. (2009). Generalized inquisi-
tive logic. In Proc. of TARK-11, pages 71–80. ACM.
Enqvist, S. (2009). Interrogative Belief Revision in Modal
Logic. Journal of Phil. Logic, 38(5):527–548.
Farias del Cerro, L., Fauthoux, D., Gasquet, O., Herzig,
A., Longin, D., and Massacci, F. (2001). Lotrec: the
generic tableau prover for modal and description log-
ics. In International Joint Conference on Automated
Reasoning, LNCS, page 6. Springer Verlag.
Genot, E. (2009). The game of inquiry: the interrogative ap-
proach to inquiry and belief revision theory. Synthese,
171(2):271–289.
Gerdes, A., Heeren, B., Jeuring, J., and Stuurman, S.
(2008). Feedback services for exercise assistants. In
Proc. of the 7th European Conference on e-Learning.
Agia Napa, Cyprus.
Groenendijk, J. (2008). Inquisitive semantics: Two possi-
bilities for disjunction. In 7th Tbilisi Symposium on
Language, Logic, and Computation. Springer.
Hintikka, J., Halonen, I., and Mutanen, A. (2002). Interrog-
ative logic as a general theory of reasoning. Handbook
of the Logic of Argument and Inference: The Turn To-
wards the Practical, page 295.
Icard, T. (2009). Inquisitive Announcement Logic.
manuscript.
Knuth, K. (2005). Toward question-asking machines: the
logic of questions and the inquiry calculus. In 10th
International Workshop on Artificial Intelligence and
Statistics, Barbados. Citeseer.
Peli
ˇ
s, M. (2009). Epistemic Logic and Questions.
Stein, W. and Joyner, D. (2005). Sage: System for alge-
bra and geometry experimentation. In ACM SIGSAM
Bulletin, vol. 39. ACM.
Unger, C. and Giorgolo, G. (2008). Interrogation in Dy-
namic Epistemic Logic. 13th ESSLLI Student Session.
van Benthem, J., Gerbrandy, J., Hoshi, T., and Pacuit, E.
(2009). Merging frameworks of interaction. In Jour-
nal of Philosophical Logic. Springer.
van Benthem, J. and Minic
˘
a, S¸. (2009). Toward a dynamic
epistemic logic of questions. In Proc. of LORI’09,
Second International Workshop on Logic, Rationality
and Interaction, LNCS/FoLLI-LNAI 5834. Springer.
van Eijck, J. (2004). Dynamic epistemic modelling.
In CWI Report SEN-E0424. Available online from:
http://www.cwi.nl/ jve/papers/04/demo/DEMO.pdf.
Wi
´
sniewski, A. (1996). The logic of questions as a theory
of erotetic arguments. Synthese, 109(1):1–25.
CSEDU 2010 - 2nd International Conference on Computer Supported Education
372