ALGORITHM APPLIED IN THE PRIORITISATION
OF THE STAKEHOLDERS
Anna María Gil Lafuente and Luciano Barcellos de Paula
Faculty of Economics and Business, University of Barcelona, Av. Diagonal 690, 08034, Barcelona, Spain
Keywords: Stakeholder Theory, Prioritisation of stakeholders, Corporate sustainability, Fuzzy Logic, P-Latin
Composition.
Abstract: According to scientific studies, relationships with all stakeholders and addressing all issues related to
sustainability in business is neither possible nor desirable. The company should seek to establish an order of
priorities for the stakeholders and issues to ensure good management of time, resources and expectations.
Based on Stakeholder Theory we discuss the importance of management with stakeholders in the pursuit of
sustainability in enterprises. In this paper we will focus our research on the prioritisation of the stakeholders
through an analysis of an empirical study by a consulting firm in Brazil. In this case, the company needs to
establish priorities for its stakeholders. To achieve this objective, the consultant hired has used fuzzy logic
algorithm, applying the P-Latin Composition. To complete the study, we present the contributions, the
empirical results and conclusions of our investigation.
1 INTRODUCTION
The stakeholder of a company is by definition any
group or individual who can affect or is affected by
the achievement of the objectives of the organisation
(Freeman, 1984). There is a generic list of
stakeholders from business, even for a single
company, because they change over time (Mitchell,
Agle and Wood, 1997). The groups and individuals
affected and affecting businesses rely on the
industry, business, geographic location and subject
matter. The new business strategies and contextual
changes often determine a new set of stakeholders.
Through the constructive engagement of
stakeholders, companies can increase external
confidence in its intentions and activities, helping to
improve corporate reputation and catalyze the
diffusion of more sustainable practices in the
enterprise system in general (Elkington, 1998). The
stakeholders of a firm are individuals and groups
who contribute voluntarily or involuntarily, to its
capacity and wealth creation activities and therefore,
are potential beneficiaries and / or risk bearers (Post,
Preston and Sachs, 2002). Interest groups cover a
wide variety of stakeholders, including shareholders,
employees, customers, local communities,
government, NGOs, suppliers. The Stakeholder
Theory predicts that sustainability should have a
positive impact on financial results because
companies benefit from address and balance the
claims of the many key stakeholders (Freeman and
Evan, 1990). Moreover, the continuing failure to
address the concerns and expectations of the groups,
ultimately, reduces the confidence of investors in
company shares, which affect their cost of funds
(weighted average cost of capital) and therefore,
opportunities for profit (SAM and PWC, 2009).
To do sustainable business, companies must have
good knowledge of all actors with influence in its
sphere of activity. This identification of stakeholders
is the first step. Once organizations have become
aware of the various publics that interact with them,
it is important to categorize in terms of expectations,
problems, geographical areas, its impact on business
activity and vice versa. The result of the
identification and segmentation is called mapping
stakeholders. To do a map involves identifying
stakeholder expectations and influence of each. This
helps establish priorities that meet, while allowing
an overall view of other possible interactions
between groups. Subsequently, companies must
establish a hierarchy among them, in order to
determine the relevance of their modes of
interaction. According to scientific studies, engaging
with all stakeholders or on all issues is neither
181
María Gil Lafuente A. and Barcellos de Paula L. (2010).
ALGORITHM APPLIED IN THE PRIORITISATION OF THE STAKEHOLDERS.
In Proceedings of the 12th International Conference on Enterprise Information Systems - Artificial Intelligence and Decision Support Systems, pages
181-186
DOI: 10.5220/0002862201810186
Copyright
c
 SciTePress

possible nor desirable. This would go beyond any
available resources, and at the same time make it
very difficult to adequately respond to stakeholders,
leading to frustration. Therefore, the enterprise
should try and prioritise its stakeholders and issues
to ensure that time, resources and expectations are
well managed (Accountability, UNEP and
Stakeholder Research Associates Canada, 2005).
Another item relevant to the topic relates to
compliance with the GRI Guidelines for
Sustainability Reporting and the requirements of
European Standard SGE 21:2008. According to the
GRI in subsection 4.15, the organization must
submit the procedure for defining its stakeholder
groups and for the determination of the groups
involved and those not. In subsection 6.1.7, SGE
21:2008 states that organisations must develop a
documented relationship with its stakeholders. This
model includes criteria for identifying and
classifying stakeholders, a methodology to detect
their expectations and the establishment and
prioritization of action plans and communication.
In this paper we will focus our research on the
prioritisation of the stakeholders through an analysis
of an empirical study by a consulting firm in Brazil.
In this case, the contracting company has gone
through the stages of identification and segmentation
of stakeholders and needs to establish a priority
order for stakeholders.
Because of the importance and complexity that is
the prioritisation of the stakeholders for companies
is essential to address the analysis with an approach
based on complex systems and models that help
entrepreneurs in making decisions. For these
reasons, it is justified to analyze the prioritisation of
the stakeholders using fuzzy logic algorithms, in this
specific case; the consultancy contract has applied
the P-Latin composition.
We believe that our contribution will serve to
support future research on the application of
algorithms to business sustainability, a field that has
been only scarcely investigated.
2 METHODOLOGY
The Fuzzy Sets Theory (Zadeh, 1965) is a
mathematical theory in the field of multivalent
logics. Its origin is in the work done by Professor
Lotfi A. Zadeh and is the starting point for a
mathematical theory currently expanding in all
scientific disciplines and built with the entire rigor
that enables the treatment of subjectivity and / or
uncertainty (Gil Lafuente, 2001).
At first, the Fuzzy Sets Theory has been applied
in the field of formal science, but in the last 45
years, researchers around the world have published
many papers and studies with applications in various
fields. It should be noted, the pioneering and
important contribution to science of the teachers
Kaufmann and Gil Aluja who published the first
book in the world dedicated exclusively to the
processing of financial and management problems
with the mathematics of uncertainty (Kaufmann and
Gil Aluja, 1986). It included very diverse studies
(investments, renewal of equipment, inventory
management and product distribution).
Currently, the use of fuzzy logic takes place in
practically every field of science studies. It is in the
business management, engineering, biology,
medicine, geology, sociology, phonetics, and even in
music, among others. Every problem is located in
the area of uncertainty is likely to be treated by the
theory of fuzzy subsets and that as time passes it is
becoming increasingly feasible to introduce in
formal schemes, mechanisms of thinking, such as
sensations and numeric views. To highlight the large
potential of new operational techniques of
management in relation to decision theory,
Kaufmann and Gil Aluja (1991) proposed the
method of the P–Latin composition.
The path is tackled that has as its starting out
point the so-called Latin matrix. To follow this path,
at least initially, we must resort to the matrix form.
The use of adequate operators, mainly the maxmin
convolution, leads to the method of the P-Latin
composition. The requirement of a specific property
(that of the elemental path) allows for the
establishment of the enumeration of the elemental
paths of a graph, which are, in themselves, an
immediate source of order. The algorithm emanating
from this does the rest (Gil Aluja, 1999).
According to (Gil Aluja, 1999), what is known as
“the latin sequence of property P” or simply “P-
Latin” is a finite sequence of vertices (a
1
, a
2,
…, a
n
)
which forms a path that possess a property P in the
graph ,
Γ
. Let us assume two paths, one of
longitude p and the other of longitude q, which
possess property P and are represented respectively
by the P-latin sequences:
s
1
= (a
1
,a
2
,…, a
p
, b)
(1)
s
2
= (c, d
1
,d
2
,…, d
q
)
(2)
We then consider a binary operation * such we
that we arrive at:
s
1
*s
2
= (a
1
, a
2
,...,a
p
, b, d
1
, d
2
, ...,d
q
)
(3)
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
182

if: b = c
and if: the sequence is P-latin.
=Ø,
if it is not.
With the object of enumerating the paths, we
start out from the notion of latin matrix [L]
1
, the
elements of which are formed by the description of
the latin letters corresponding to the row and column
that define each element. By construction, this latin
matrix [L]
1
enumerates the paths, obviously
elemental in this case, of a longitude of 1. Likewise
matrix [L´]
1
is defined as the previous matrix which
has been deprived, to element of each box, of its
respective initial letter. The composition [L]
1
o [L´]
1
provides [L]
2
, which enumerates the elemental paths
of a longitude of 2 when the property required, is
that of an elemental path. By carrying out successive
compositions we arrive at:
[L]
2
o [L´]
1
= [L]
3
[L]
3
o [L´]
1
= [L]
4
......................
[L]
r-1
o [L´]
1
= [L]
r
(4)
This allows us to enumerate the elemental paths
of a longitude of 1, 2,..., r, without omission or
repetition. For this it is necessary that the
fundamental relation is complied with.
s
1
* s
2
= s
1
. s´
2
, if s
1
. s´
2
(5)
is an elemental path
=Ø, if the contrary is true.
We now move on to present the corresponding
algorithm.
1) The latin matrix [L]
1
is constructed from the
binary relations matrix, or associated arrow
form graph.
2) Based on the latin matrix [L]
1
we arrive at the
latin matrix amputated of its initials [L´]
1
.
3) By means of the latin convolution of matrix
[L]
1
and of the amputated matrix [L´]
1
the
latin matrix [L]
2
is arrived at where property P
is the “elemental path”. The elemental paths
arrived at are of a longitude of 2.
4) By means of the latin convolution of the latin
matrix [L]
2
and [L´]
1
we arrive at matrix [L]
3
which gives us the elemental paths of a
longitude of 3.
5) We continue in this way until arriving at [L]
r-1
,
r being the cardinal of the reference set E, as
long as the latin matrix is not empty, in which
case the process is halted.
6) We now find [L]
r
in order to verify the non-
existence of circuits.
The P-Latin composition can be applied in
management processes and provides a useful model
in making decisions, for example, the prioritisation
of the stakeholders into consideration criteria of
sustainability in business.
3 THE PRIORITISATION OF
THE STAKEHOLDERS
There are a range of frameworks, standards and
codes, which organisations can draw on to provide
guidance for the process of stakeholder engagement
and which aim to improve the sustainability
performance of the organisation (Accountability,
UNEP and Stakeholder Research Associates
Canada, 2005). These include the GRI
Sustainability Reporting Guidelines (on reporting),
SA8000 (on labour standards compliance), the
AA1000 Series (on systematic accountability,
including engagement), and the EFQM Excellence
Model (on quality management). At the national
level various bodies have issued guidance and
standards on social responsibility, for example the
SD21000 in France, SIGMA in the UK, AS8003 in
Australia and Standard SI 10000 in Israel. At an
international level, these will be complemented by
the current ISO process to develop international
guidance on social responsibility, in which
stakeholder engagement will feature prominently.
There are also a number of useful resources from
organisations including The World Business Council
for Sustainable Development, Business for Social
Responsibility, CSR Europe, The Future 500
Initiative, the UK Environment Council, the South
African Calabash Project, the Brazilian Institute
Ethos, the Indian Development Alternatives Group
and the International Association for Public
Participation.
To establish priorities among the stakeholders is
important to define the criteria for this process
(Accountability, UNEP and Stakeholder Research
Associates Canada, 2005). The level of influence,
dependency or willingness to participate is good
starting points, but you may need to use other
criteria. According to the concept of impact and
relevance to the company (Olcese, Rodríguez Ángel
and Alfaro, 2008) could be established priorities in
different types of stakeholders:
- Critics are those who, for example, have a key
impact economic, strengthen the reputation or
influence, or grant licenses or limited access or
create the future of the sector.
ALGORITHM APPLIED IN THE PRIORITISATION OF THE STAKEHOLDERS
183

- Basic: those with an average impact on
business results, which may partially affect the
reputation, but somehow affecting key processes
in the company.
- Complementary: are those that have minimal
economic impact, had little impact on the
reputation and can provide complementary
services or products.
4 FUZZY LOGIC APPLIED TO
SUSTAINABILITY
In relation to the fuzzy logic applied to
sustainability, the review of the literature, we find
authors who have used it in many ways, as in models
for analysing purchase decision in consumers of
ecologic products (Gil Lafuente and Salgado
Beltrán, 2005) and (Gil Lafuente, Salgado Beltrán,
Subirá Lobera and Beltrán, 2006), in environmental
principles applicable to green supplier evaluation by
using multi-objective decision analysis (Lu, Wu and
Kuo, 2007), in selection process elements that
contribute to sustainable growth of the company
(Barcellos Paula and Gil Lafuente, 2009a) and in
applied algorithms in the sustainable management of
human resources (Barcellos Paula and Gil Lafuente,
2009b). However, the application of fuzzy logic to
sustainability in business, mainly addressing the
prioritisation of stakeholders, yet has been little
investigated.
In this context, the consultant hired has chosen to
prioritize the stakeholders at the discretion of impact
and relevance to the company. The aim is to
establish a priority order for stakeholders by
applying fuzzy logic through the P-Latin
composition.
The methodology has the following advantages:
it helps in making decisions in a changing
environment, conflict and uncertainty, allows
interaction between different stakeholders in finding
a consensus among themselves on a specific topic,
the analysis helps complex systems such as the
prioritisation of stakeholders, provides flexibility to
model various scenarios ongoing business, among
others. The limitation of the methodology is given
when we confirm the existence of a circuit that
passes through all vertices. In this case, the evidence
leads to the impossibility of establishing order.
5 THE EMPIRICAL STUDY
The empirical study was conducted in August 2009
by the Ideas and Solutions Consulting in Brazil. At
the request of the contractor, the study data were
treated with strict confidentiality. The company
belongs to food industry and the objective is to
establish a priority order for the following
stakeholders: (a) governance, (b) NGOs, (c) local
communities, (d) employees, and (e) suppliers. This
will include a prioritisation of stakeholders to
discuss the issue of CO
2
emissions reduction.
Consulting convened a workshop that was attended
by five heads of departments who know the
stakeholders and subject matter. Once submitted to
the directors of the company the subject and the list
of stakeholder groups, we ask you to indicate your
view with the scale [0,1], considering the impact and
relevance criteria for the company, according to
which , as the closer estimate 1, the greater the
importance of one group over others on the topic
under analysis.
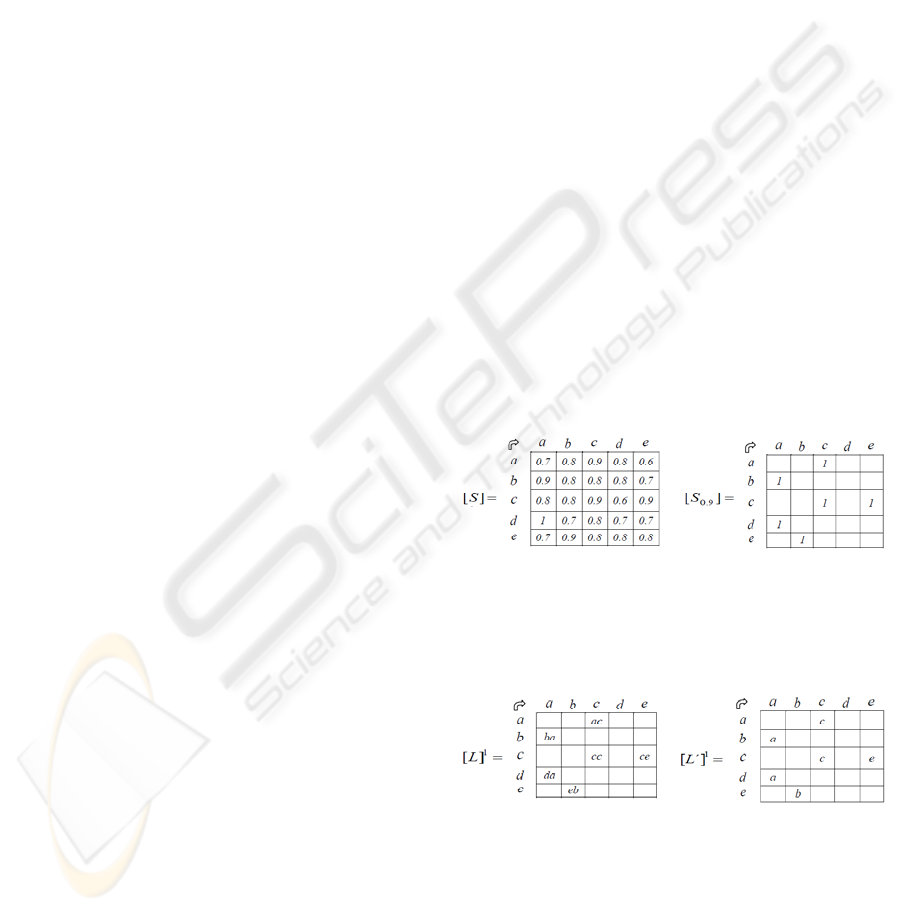
The result (Kaufmann, 1987) is the matrix
representing this rating. As with all fuzzy
relationship, it's possible to treat their α-cuts. The
company decided to perform the analysis level (α ≥
0.9) which is considered a high level. As a result, we
find the Boolean matrix [S
0.9
] (figure 1).
Figure 1: Boolean matrix.
Starting out from matrix [S
0.9
] we construct the
latin matrix [L]
1
. From the matrix [L]
1
we find the
amputated matrix to the left [L´]
1
(figure 2).
Figure 2: Amputated matrix.
We do the latin convolution [L]
1
o [L´]
1
and
arrive at [L]
2
. This matrix shows all combinations of
factors that affect others in two phases and with a
level of 0.9 (figure 3).
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
184

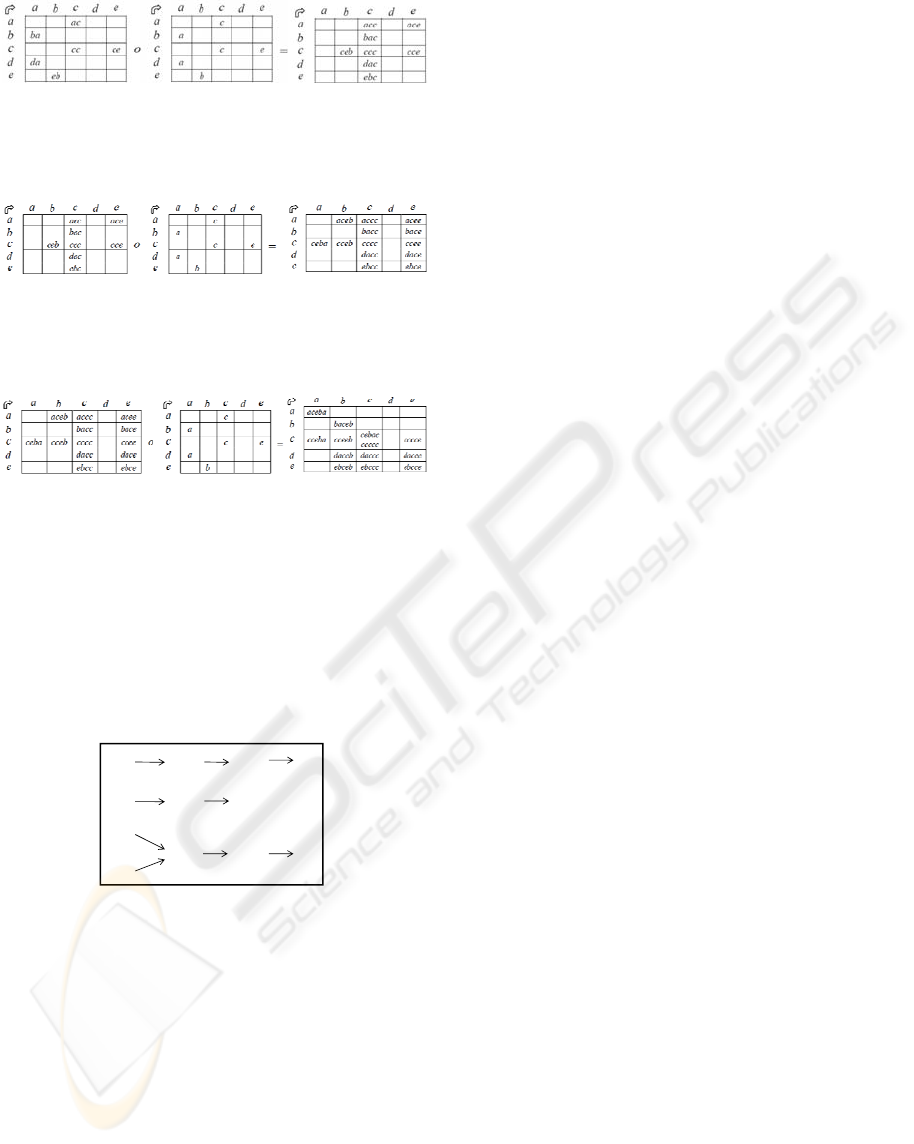
Figure 3: Latin convolution 2.
We now find the latin convolution [L]
2
о [L´]
1
=
[L]
3
(figure 4).
Figure 4: Latin convolution 3.
We then obtain the latin convolution [L]
3
о [L´]
1
= [L]
4
(figure 5).
Figure 5: Latin convolution 4.
6 RESULTS
We note that the result found in the matrix [L]
4
exposes the presence of circuits. In this case, we stop
the process in order to study the last latin matrix that
is not empty, in our case [L]
3
. In it we can see that
there are four paths (figure 6):
Figure 6: Four paths.
Which leads us to conclude that this is “partial
order”: (a) governance, (c) local communities, and
(e) suppliers. The methodology allows for flexibility
in the implementation of algorithms, since under the
circumstances, valuations and criteria, valuations
can change and consequently the result too.
7 CONCLUSIONS
The study about the stakeholder show that compared
with the changes we are living is essential to find
models that will help employers in making
decisions, especially in an uncertain environment.
Because of the importance and complexity that is the
prioritization of the stakeholders for companies in
our research we try to analyze these complex
systems using fuzzy logic. In applying the model
through empirical study has been possible to provide
a tool based on the use of categorization algorithm
that can facilitate decision making by obtaining
qualitative data from a dialogue with managers or
specialists on a particular topic. This is an
innovation and a useful tool to be used in the process
of prioritization of stakeholders. The result showed
four possible solutions, being that it has
demonstrated a strong prioritization (organisation)
for the following groups: (a) governance, (c) local
communities and (e) suppliers, respectively.
The article's main contribution is the application
of algorithms in the prioritization of stakeholders
considering sustainability criteria in enterprises, and
providing a useful model in making decisions. We
believe that our contribution will serve to support
future research in the field of application of
algorithms to business sustainability in general and
particular aspects of it such as environmental
management, economic and social, among many
other approaches.
ACKNOWLEDGEMENTS
Luciano Barcellos de Paula is as a scholar of
MAEC-AECI.
REFERENCES
Accountability, United Nations Environment Programme,
Stakeholder Research Associates Canada Inc., 2005.
The Stakeholder engagement Manual. From words to
action. The practitioner's handbook on stakeholder
engagement. Vol. 2, p.39.
Barcellos Paula, L. and Gil Lafuente, A. M., 2009a.
Proceso de selección de elementos que contribuyen al
crecimiento sostenible de la empresa. Proceeding of
International Conference and Doctoral Consortium
for ISEOR and Academy of Management, held at
Lyon, France, (1), 773-788.
Barcellos Paula, L.; Gil Lafuente, A. M., 2009b.
Algoritmos aplicados en la gestión sostenible de los
recursos humanos. Economic and Financial Crisis:
New challenges and Perspectives. Proceeding of XV
Congress of International Association for Fuzzy-Set
Management and Economy (SIGEF), Lugo, Spain,
104-115.
abce
c
e
b
ec
b
a
d
ALGORITHM APPLIED IN THE PRIORITISATION OF THE STAKEHOLDERS
185

Elkington, J., 1998. Cannibals with forks: the triple
bottom line of 21st Century Business. Oxford, U.K.
Capstone Publishing Limited.
Freeman, R. E., 1984. Strategic Management: A
Stakeholder Approach. Pitman Series in Business and
Public Policy.
Freeman, R. E.; Evan, W., 1990. Corporate Governance:
A Stakeholder Interpretation. Journal of Behavioral
Economics. 19 (4), 337 – 359.
Gil Lafuente, A. M., 2001. Nuevas estrategias para el
análisis financiero en la empresa. Editorial Ariel.
Barcelona.
Gil Lafuente, A. M.; Salgado Beltrán, L., 2005. Models
for analysing purchase decision in consumers of
ecologic products. Fuzzy Economic Review, X, 47-62.
Gil Lafuente, A. M.; Salgado Beltrán, L.; Subirá Lobera,
E.; Beltrán, L. F., 2006. Teoría de efectos olvidados en
el consumo sustentable de productos ecológicos. In
Desarrollo sustentable: ¿Mito o realidad? Ed. Centro
de investigaciones biológicas del noroeste, S.C.
Mexico, 223-240.
Gil Aluja, J., 1999. Elements for a Theory of decision in
uncertainty. Kluwer Academic Publishers.
Global Reporting Initiative, 2006. Sustainability Reporting
Guidelines, version 3.0.
Kaufmann, A., 1987. Les expertones. Ed. Hermés. París.
Kaufmann, A.; Gil Aluja, J., 1986. Introducción de la
teoría de los subconjuntos borrosos a la gestión de las
empresas. Editorial Milladoiro. Santiago de
Compostela, Spain.
Kaufmann, A.; Gil Aluja, J., 1991. Nuevas técnicas para
la dirección estratégica. Ed. Universidad de
Barcelona. Barcelona.
Lu, L.; Wu, C.; Kuo, T., 2007. Environmental principles
applicable to green supplier evaluation by using multi-
objective decision analysis. International Journal of
Production Research. 45(18-19), 4317-4331.
Mitchell, R. K., Agle, B. R.; Wood, D. J., 1997. Toward a
Theory of Stakeholder Identification and Salience:
Defining the Principle of who and what really Counts.
The Academy of Management Review. 22(4), 853-886.
Olcese, A.; Rodríguez Ángel, M.; Alfaro, J., 2008. Manual
de la empresa Responsable y Sostenible. Madrid:
McGraw-Hill.
Post, J. E., Preston, L. E.; Sachs, S., 2002. Managing the
Extended Enterprise: The New Stakeholder View.
California Management Review. 45(1), 5-28.
SAM (Sustainability Asset Management); PWC
(PricewaterhouseCoopers), 2009. The Sustainability
Yearbook. Zurich, p. 13.
SGE 21, 2008. Sistema de Gestión Ética y Socialmente
Responsable. Ed. FORÉTICA. Foro para la
Evaluación de la Gestión Ética, Madrid.
Zadeh, L. A., 1965. Fuzzy sets. Information and Control,
8 (3), (1965) 338-353.
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
186