
MULTI-PROCESS OPTIMIZATION
VIA HORIZONTAL MESSAGE QUEUE PARTITIONING
Matthias Boehm, Dirk Habich and Wolfgang Lehner
Database Technology Group, Dresden University of Technology, Dresden, Germany
Keywords:
Integration processes, Multi-process optimization, Message queues, Throughput improvement.
Abstract:
Message-oriented integration platforms execute integration processes—in the sense of workflow-based pro-
cess specifications of integration tasks—in order to exchange data between heterogeneous systems and ap-
plications. The overall optimization objective is throughput maximization, i.e., maximizing the number of
processed messages per time period. Here, moderate latency time of single messages is acceptable. The ef-
ficiency of the central integration platform is crucial for enterprise data management because both the data
consistency between operational systems and the up-to-dateness of analytical query results depend on it. With
the aim of integration process throughput maximization, we propose the concept of multi-process optimiza-
tion (MPO). In this approach, messages are collected during a waiting period and executed in batches to
optimize sequences of process instances of a single process plan. We introduce a horizontal—and thus, value-
based—partitioning approach for message batch creation and show how to compute the optimal waiting time
with regard to throughput maximization. This approach significantly reduces the total processing time of a
message sequence and hence, it maximizes the throughput while accepting moderate latency time.
1 INTRODUCTION
The scope of data management is continuously chang-
ing from the management of locally stored data to-
wards the management of distributed information
across multiple heterogeneous applications and sys-
tems. In this context, typically, integration processes
are used in order to specify and execute complex in-
tegration tasks. These integration processes are exe-
cuted by message-oriented integration platforms such
as EAI servers (Enterprise Application Integration) or
MOM systems (Message-Oriented Middleware). For
two reasons, many independent instances of integra-
tion processes are executed over time. First, there
is the requirement of immediate data synchronization
between operational source systems in order to ensure
data consistency. Second, data changes of the opera-
tional source systems are directly propagated into the
data warehouse infrastructure in order to achieve high
up-to-dateness of analytical query results (real-time
ETL). Due to this high load of process instances, the
performance of the central integration platform is cru-
cial. Thus, optimization is required.
In the context of integration platforms, the ma-
jor optimization objective is throughput maximization
(Lee et al., 2007) rather than the execution time min-
imization of single process instances. Thus, the goal
is to maximize the number of messages processed per
time period. Here, moderate latency times of single
messages are acceptable (Cecchet et al., 2008).
When optimizing integration processes, the fol-
lowing problems have to be considered:
Problem 1. Expensive External System Access. The
time-expensive access of external systems is caused
by network traffic and message transformations from
external formats into internal structures. The fact that
external systems are accessed with similar queries
over time offers potential for optimization.
Problem 2. Cache Coherency Problem. One solution
to Problem 1 might be the caching of results of ex-
ternal queries. However, this fails, because when in-
tegrating highly distributed systems and applications,
the central integration platform cannot ensure that the
cached data is consistent with the data in the source
systems (Lee et al., 2007).
Problem 3. Serialized External Behavior. In depen-
dence on the external systems (e.g., caused by ref-
erential integrity constraints), we need to ensure the
serial order of messages. However, internal out-of-
order processing is possible.
Given these problems, throughput maximization
5
Boehm M., Habich D. and Lehner W. (2010).
MULTI-PROCESS OPTIMIZATION VIA HORIZONTAL MESSAGE QUEUE PARTITIONING.
In Proceedings of the 12th International Conference on Enterprise Information Systems - Databases and Information Systems Integration, pages 5-14
DOI: 10.5220/0002862600050014
Copyright
c
SciTePress

of integration processes has so far only been ad-
dressed by a higher degree of parallelism (Li and
Zhan, 2005; Srivastava et al., 2006) or pipelining
(Biornstad et al., 2006; Boehm et al., 2009). Although
this can significantly increase the resource utilization
and thus, optimize the throughput, it does not reduce
the work to be executed by the integration platform.
In this paper, we introduce the concept of Multi-
Process Optimization (MPO) in order to maximize the
message throughput. Therefore, we periodically col-
lect incoming messages and execute the whole mes-
sage batch with one single process instance. The
novel idea is to use horizontal (value-based) message
queue partitioning as a batch creation strategy and to
compute the optimal waiting time. When using this
approach, all messages of one batch (partition) exhibit
the same attribute value with regard to a chosen parti-
tion attribute. Hence, the complexity of several opera-
tors is reduced. This yields throughput improvements
because the relative processing costs per message de-
crease with increasing batch size. In detail, we make
the following contributions:
• Section 2 presents a typical architecture and exe-
cution characteristics of an integration platform.
• In Section 3, we give a solution overview of MPO
that leads to the horizontal partitioning approach.
• Then, in Section 4, we define the MPO problem.
Here, we also explain the cost estimation and the
computation of the optimal waiting time.
• In Section 5, we introduce the concept of a parti-
tion tree. We discuss the derivation of partitioning
attributes and the rewriting of process plans.
• Afterwards, we illustrate the results of our exhaus-
tive experimental evaluation in Section 6.
Finally, we analyze related work in Section 7 and con-
clude the paper in Section 8.
2 SYSTEM ARCHITECTURE
A typical integration platform system architecture
consists of a set of inbound adapters, multiple mes-
sage queues, an internal scheduler, a central process
execution engine, and a set of outbound adapters. The
inbound adapters passively listen for incoming mes-
sages, transform them into a common format (e.g.,
XML) and append the messages to message queues or
directly forward them to the process engine. Within
the process engine, compiled process plans of de-
ployed integration processes are executed. While ex-
ecuting those processes, the outbound adapters are
used as services/gateways in order to actively invoke
Receive (o1)
[service: s1, out: msg1]
Assign (o2)
[in: msg1 out: msg2]
Join (o4)
[in: msg1, msg3; out: msg4]
Invoke (o3)
[service: s2, in: msg2, out: msg3]
Invoke (o5)
[service s3, in: msg4]
Q
i
:
SELECT *
FROM s2.Credit
WHERE Customer=?
with
? = m
i
/Customer/Cname
Q
i
External
System
s1
Inbound
Adapter
Outbound
Adapter
Outbound
Adapter
External
System
s2
External
System
s3
Figure 1: Running Example Process Plan P.
external systems. Therefore, they transform the inter-
nal format back into the proprietary message repre-
sentations. This architecture is similar to the architec-
ture of major products such as SAP Process Integra-
tion, IBM Message Broker or MS Biztalk Server.
The following example explains the instance-
based (step-by-step) process execution, where mes-
sage queues are used at the inbound server side only.
Example 1. Orders Processing: Assume a process
plan P that consists of an operator sequence o with
o
i
∈ (o
1
,...,o
5
) (Figure 1). In the instance-based
case, a new process instance p
i
is created for each
message (Figure 2). The Receive operator (o
1
) gets
an orders message from the queue and writes it to a lo-
cal variable. Then, the Assign operator (o
2
) is used
in order to prepare a query with the customer name of
the received message as a parameter. Subsequently,
the Invoke operator (o
3
) queries an external system
s
2
in order to load additional customer data. Here,
one SQL query Q
i
per process instance (per message)
is used. The Join operator (o
4
) merges the result
message with the received message. A final Invoke
operator (o
5
) sends the join result to system s
3
. We
see that multiple orders from one customer (CustA:
m
1
→ p
1
, m
3
→ p
3
) cause us to pose the same query
(o
3
) multiple times to external system s
2
.
At this point, multi-process optimization comes
into play, where we optimize the whole sequence of
asynchronous process instances.
Q
1
: SELECT *
FROM s2.Customer
WHERE CName=“CustA“
m1 [“CustA“]
m2 [“CustB“]
m3 [“CustA“]
m4 [“CustC“]
m5 [“CustB“]
m6 [“CustC“]
Standard Message Queue
enqueue
dequeue
m1
o1 o3 o5o2 o4
p1:
dequeue
m2
Q
2
: SELECT *
FROM s2.Customer
WHERE CName=“CustB“
o1 o3 o5o2 o4
p2:
o1 o3 o5o2 o4
p3:
dequeue
m3
Q
3
: SELECT *
FROM s2.Customer
WHERE CName=“CustA“
Figure 2: Instance-Based Process Plan Execution of P.
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
6

3 MULTI-PROCESS
OPTIMIZATION
The na
¨
ıve (time-based) batching approach, as already
proposed for distributed queries (Lee et al., 2007),
is to collect messages during a waiting time T
W
and
merge those messages to message batches b
i
. Then,
we execute a process instance p
0
i
of the modified pro-
cess plan P
0
for the message batch b
i
. Due to the sim-
ple (time-based) model of collecting messages, there
might be multiple distinct messages in the batch ac-
cording to the attributes used by the operators of P
0
.
It follows that we need to rewrite the queries to exter-
nal systems. We cannot precisely estimate this influ-
ence due to a lack of knowledge about data properties
of external systems (Ives et al., 2004). In conclusion,
the na
¨
ıve approach can also hurt performance.
To tackle this problem, we propose a novel
concept—the horizontal message queue partitioning
approach—that we use in the rest of the paper.
The basic idea is to horizontally partition the in-
bound message queues according to partitioning at-
tributes ba
i
. With such value-based partitioning, all
messages of a batch exhibit the same attribute value
according to the partitioning attribute. Thus, certain
operators of the process plan only need to access this
attribute once for the whole partition rather than for
each individual message. The core steps are (1) to de-
rive the partitioning attribute from the process speci-
fication, (2) to periodically collect messages during a
waiting time T
W
, (3) to read the first partition from the
queue, and (4) to execute the messages of this parti-
tion as a batch with an instance p
0
i
of a modified pro-
cess plan P
0
. Additionally, (5) we might need to en-
sure the serial order of messages at the outbound side.
Example 2. Partitioned Batch-Orders Processing:
Figure 3 reconsiders the running example for parti-
tioned multi-process execution. The incoming mes-
sages m
i
are partitioned according to the partition-
ing attribute customer name that was extracted with
ba = m
i
/Customer/Cname at the inbound side. A
process instance of the rewritten process plan P
0
reads
the first partition from the queue and executes the sin-
gle operators for this partition. Due to the equal val-
ues of the partitioning attribute, we do not need to
rewrite the query to the external system s
2
. Every
batch contains exactly one distinct attribute value ac-
cording to ba. In total, we achieve performance bene-
fits for the Assign as well as the Invoke operators.
Thus, the throughput is improved and does not depend
on the number of distinct messages. Note that the in-
coming order of messages was changed and needs to
be serialized at the outbound side.
The horizontal partitioning has another nice prop-
CustC
CustB
CustA
m1 [“CustA“]
m3 [“CustA“]
m2 [“CustB“]
m5 [“CustB“]
m4 [“CustC“]
m6 [“CustC“]
Partitioned Message Queue
enqueue
Wait
T
W
Q’
1
: SELECT *
FROM s2.Customer
WHERE CName=“CustA“
dequeue
b1
o1 o3 o5o2 o4
p’1:
dequeue
b2
o1 o3 o5o2 o4
p’2:
Q’
2
: SELECT *
FROM s2.Customer
WHERE CName=“CustB“
Figure 3: Partitioned Message Batch Execution P
0
.
erty: Several operators (e.g., Assign, Invoke, and
Switch) benefit from partitioned message batch exe-
cution. There, partitioning attributes are derived from
the process plan specification (e.g., query predicates
and switch expressions). The benefit is caused by
executing operations on partitions rather than on in-
dividual messages, and therefore, is similar to pre-
aggregation (Ives et al., 2004) or early-group-by
(Chaudhuri and Shim, 1994) in DBMS.
Clearly, MQO (Multi-Query Optimization) and
OOP (Out-of-Order Processing) (Li et al., 2008) have
already been investigated in the context of DBMS and
DSMS. However, in contrast to existing work, we
present a novel MPO approach that maximizes the
throughput by computing the optimal waiting time.
Furthermore, this approach is dedicated to the con-
text of integration processes, where such an execution
model has been considered for the very first time.
MPO is also related to caching and the recycling
of intermediate results (Ivanova et al., 2009). While
caching might lead to using outdated data, the par-
titioned execution might cause us to use data that is
more current than it was when the message arrived.
However, we cannot ensure strong consistency by us-
ing an asynchronous integration technique (message
queues). Further, we guarantee that (1) the tempo-
ral gap is at most equal to a given latency constraint
and that (2) no outdated data is read. In conclusion,
caching is advantageous if data of external sources
is static, while MPO is beneficial if data of external
sources changes dynamically.
Finally, the question arises of how likely it is that
we can benefit from MPO. With regard to the exper-
imental evaluation, there are three facts why we ben-
efit from MPO. First, even for 1-message partitions,
there is only a moderate runtime overhead. Second,
throughput optimization is required if and only if high
message load (peaks) exists. In such cases, it is very
likely that messages with equal attribute values are in
the queue. Third, only a small number of messages
is required within one partition to yield a significant
speedup for different types of operators.
The major research challenges of MPO via hor-
izontal partitioning are (1) to compute the optimal
waiting time and (2) to enable partitioned process ex-
MULTI-PROCESS OPTIMIZATION VIA HORIZONTAL MESSAGE QUEUE PARTITIONING
7

ecution. Both are addressed in the following sections.
4 WAITING TIME
COMPUTATION
Based on a formal problem description, we describe
how to automatically compute the optimal waiting
time w.r.t. maximizing the throughput.
Let M with m
i
∈ (m
1
,m
2
,...) be an infinite and
ordered stream of messages. We model each message
m
i
as a (t
i
,d
i
)-tuple, where t
i
∈ N denotes the incom-
ing timestamp of the message and d
i
denotes a semi-
structured tree of name-value data elements. Each
message m
i
is processed by an instance p
i
of a pro-
cess plan P, and t
out
(m
i
) ∈ N denotes the timestamp
when the message has been successfully processed.
The latency of a single message T
L
(m
i
) is given by
T
L
(m
i
) = t
out
(m
i
) − t
i
. This includes waiting time as
well as processing time. Then, the total latency time
of a finite message subsequence M
0
with M
0
⊆ M is
determined by T
L
(M
0
) = t
out
(m
|M
0
|
) −t
1
.
Definition 1. Multi-Process Optimization Problem
(MPO-P): Maximize the message throughput with re-
gard to a finite message subsequence M
0
. The opti-
mization objective φ is to minimize the total latency
time:
φ = max
|M
0
|
∆t
= min T
L
(M
0
). (1)
There, two additional restrictions must hold:
1. Let lc denote a soft latency constraint that must
not be exceeded significantly. Then, the condition
∀m
i
∈ M
0
: T
L
(m
i
) ≤ lc must hold.
2. The external behavior must be serialized accord-
ing to the incoming message order, where ∀m
i
∈
M
0
: t
out
(m
i
) ≤ t
out
(m
i+1
) must hold.
In order to solve the MPO-P, we horizontally par-
tition the message queue and periodically compute the
optimal waiting time T
W
with regard to the current ex-
ecution statistics. Then, an instance p
0
i
of a partitioned
process plan P
0
is issued with a period of T
W
in order
to execute the message partition b
i
. In order to avoid
temporally overlapping process plan executions and
inconsistency between the latency constraint lc and
the processing time T
P
, we define the validity condi-
tion: For a given latency constraint lc, there must ex-
ist a waiting time T
W
such that (0 ≤ T
P
≤ T
W
) ∧ (0 ≤
ˆ
T
L
≤ lc); otherwise, the constraint is invalid.
Minimizing the total latency requires the cost esti-
mation of a partitioned process plan for specific batch
sizes k
0
with k
0
= |b
i
|. First, we monitor the incom-
ing message rate R and the value selectivity sel ∈ R
with 0 < sel ≤ 1 according to the partitioning at-
tributes. Assuming a uniform distribution function D
of R, the first partition will contain k
0
= R · sel · T
W
Relative Processing Time
T
P
(P’,k’) / k’
500400300200100
100
200
300
400
500
Waiting
Time T
W
instance-based
partitioned
lower bound
(a) T
W
→ T
P
Influence
Total Latency Time T
L
Waiting
Time T
W
500400300200100
450
200
300
400
850
instance-
based
partitioned (v2)
latency
constraint
lc
min T
L
^
partitioned (v1)
^
(b) T
W
→ T
L
Influence
Figure 4: Waiting Time Search Space.
messages. For the i-th partition with i ≥
1
sel
, k
0
is
computed by k
0
= R · T
W
, independently of the selec-
tivity sel. Second, for reading Invoke, Assign and
Switch operators, the costs are independent of k
0
with
C(o
0
i
,k
0
) = C(o
0
i
,1), while for all other operators, costs
increase linearly with C(o
0
i
,k
0
) = C(o
0
i
,1)·k
0
. For each
operator, a specific cost function is defined based on
monitored cardinalities. Then, the costs of a process
plan are defined as C(P
0
,k
0
) =
∑
m
0
i=1
C(o
0
i
,k
0
).
The intuition of our method for computing the op-
timal waiting time T
W
is that the waiting time—and
hence, the batch size k
0
—strongly influences the pro-
cessing time of single process instances. Then, the
latency time mainly depends on that processing time.
Figure 4 conceptually illustrates the resulting two in-
verse influences that our computation algorithm ex-
ploits: First, an increasing waiting time T
W
causes
a decreasing relative processing time T
P
/k
0
for par-
titioned process execution (Figure 4(a)). Second, an
increasing waiting time T
W
linearly increases the la-
tency time
ˆ
T
L
because the waiting time is directly in-
cluded in
ˆ
T
L
(Figure 4(b)). The result of these two
influences is a non-linear total latency time function
that might have a minimum (v1) or not (v2). Given
the latency constraint, we can compute the optimal
waiting time with regard to latency time minimization
and hence, throughput maximization.
In detail, we can compute the waiting time where
ˆ
T
L
is minimal or where it is equal to lc by
T
W
=
(
T
W
with min
ˆ
T
L
(T
W
) 0 ≤
ˆ
T
L
≤ lc
T
W
with
ˆ
T
L
(T
W
) = lc otherwise.
(2)
The estimated total latency time
ˆ
T
L
is computed by
ˆ
T
L
=
|M
0
|
k
0
· T
W
+ T
P
(P
0
,k
0
) with
T
P
(P
0
,k
0
) = T
P
(P) ·
C(P
0
,k
0
)
C(P)
=
m
∑
i=1
T
P
(o
i
) ·
C(o
0
i
,k
0
)
C(o
i
)
,
(3)
where
d
|M
0
|/k
0
e
denotes the total number of executed
partitions. Furthermore, we can substitute k
0
with R ·
T
W
within T
P
and get
T
P
(P
0
,k
0
) = T
P
(P
0
,R · T
W
) =
m
∑
i=1
T
P
(o
i
) ·
C(o
0
i
,R · T
W
)
C(o
i
)
. (4)
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
8

Then, in order to solve the MPO-P, we compute T
W
where
ˆ
T
0
L
(T
W
) = 0 and
ˆ
T
00
L
(T
W
) > 0. Finally, we check
the validity condition and modify the waiting time T
W
if required. It can be shown for arbitrary distribution
functions D that the latency time constraint holds.
5 PARTITIONED EXECUTION
In order to enable partitioned process execution, in
this section, we introduce the partition tree and the re-
lated algorithms. The partition tree is a multi-dimen-
sional B
*
-Tree (MDB-Tree) (Scheuermann and Ouk-
sel, 1982), where the messages are horizontally par-
titioned according to multiple partitioning attributes.
Similar to a traditional MDB-Tree, each tree level rep-
resents a different partition attribute.
Definition 2. Partition Tree: The partition tree is an
index of h levels, where each level represents a par-
tition attribute ba
i
with ba
i
∈ (ba
1
,ba
2
,...,ba
h
). For
each attribute ba
i
, a set of batches (partitions) b are
maintained. Those partitions are ordered according
to their timestamps of creation t
c
(b
i
) with t
c
(b
i−1
) ≤
t
c
(b
i
) ≤ t
c
(b
i+1
). Only the last index level ba
h
con-
tains the single messages. A partition attribute has a
type(ba
i
) ∈ {value, value-list, range}.
Partitioned Queue Q
1
ENQUEUE DEQUEUE
ba
1
(Customer)
ba
2
(Totalprice )
t
c
(b
6
)
Inbound
Adapters
Process
Engine
partition b
6
[“CustB“] partition b
1
[“CustA“]partition b
2
[“CustC“]
partition b
6.2
[“<10“]
partition b
6.1
[“[10,200)“]
msg12 [„CustB“] msg5 [„CustB“]
msg9 [„CustB“]
partition b
1.1
[“<10“]
partition b
1.2
[“>200“]
partition b
1.3
[“[10,200)“]
msg1 [„CustA“]
msg2 [„CustA“]
msg6 [„CustA“]
msg11 [„CustA“]
msg4 [„CustA“]
msg8 [„CustA“]
msg10 [„CustA“]
msg3 [„CustA“]
msg7 [„CustA“]
t
c
(b
2
)t
c
(b
1
)
t
c
(b
6.2
)t
c
(b
6.1
) t
c
(b
1.3
)t
c
(b
1.2
)t
c
(b
1.1
)
>>
>>>
Figure 5: Example Queue Partition Tree (h = 2).
Example 3. Partition Tree with h = 2: Assume two
partitioning attributes ba
1
(customer, value) and
ba
2
(total price, range) from a process plan P. Then,
the partitioned tree exhibits a height of h = 2 (see Fig-
ure 5). On the first index level, the messages are parti-
tioned according to customer names, and on the sec-
ond level, each partition is divided according to the
range of order total prices.
There are two essential maintenance procedures
of the partition tree: enqueue ENQ() and dequeue
DEQ(). ENQ() is invoked by the inbound adapters for
each incoming message, while DEQ() is invoked by
the process engine periodically, according to the com-
puted optimal waiting time T
W
. The ENQ() function
scans over the partitions and determines whether or
not a partition with ba(b
i
) = ba(m
i
) already exists.
If so, the message is inserted recursively; otherwise,
a new partition is created and added at the last po-
sition. The DEQ() function returns the first partition
(min
|b|
i=1
t
c
(b
i
)) of the partition tree.
The partitioning attributes are automatically de-
rived from the single operators o
i
∈ P that benefit
from partitioning. The final partitioning scheme is
then created by minimizing the expected number of
partitions in the index. Therefore, we order the index
attributes according to their selectivities with
min
h
∑
i=1
|b
j
∈ ba
i
| with sel(ba
1
) ≥ sel(ba
i
) ≥ sel(ba
h
). (5)
Thus, we minimized the overhead of queue main-
tenance and maximized k
0
of the top-level partitions.
The result is the optimal partitioning scheme.
Subsequently, we rewrite P to P
0
in order to enable
partitioned process execution according to this parti-
tioning scheme. Therefore, we use a split and merge
approach: A process plan receives the top-level par-
tition and executes all operators that benefit from the
top-level attribute. Right before an operator that ben-
efits from the next-level partition attribute, we insert a
Split operator that splits the top-level partition into
the
1
sel(ba
2
)
subpartitions (worst case) as well as an
Iteration operator (foreach). The iteration body is
the sequence of operators that benefit from this granu-
larity. Right after this iteration, we insert a Merge op-
erator to re-group the resulting partitions if required.
Example 4. Rewriting a Process Plan: Assume the
process plan P shown in Figure 6(a). We receive
a message from system s
1
, create a parameterized
query, and request system s
2
. Afterwards, we use an
alternative switch path, and finally, we send the re-
sult to system s
3
. According to Example 3, we have
derived the two partitioning attributes ba
1
(customer,
value) and ba
2
(total price, range). If we use the
partitioning scheme (ba
1
, ba
2
), the split and merge
approach is applied as shown in Figure 6(b).
According to the requirement of serialized exter-
nal behavior, we might need to serialize messages at
the outbound side. Therefore, we extended the mes-
sage structure by a counter c. If a message m
i
out-
Receive (o1)
[s1, out:msg1]
Switch (o4)
[in:msg2]
Translation (o5)
[in: msg2, out: msg4]
Translation (o6)
[in: msg2, out: msg4]
Assign (o8)
[in: msg3,msg4 out: msg5]
Invoke (o9)
[s3, in: msg5]
Assign (o2)
[in:msg1 out:msg2]
Invoke (o3)
[s2, in:msg2, out:msg3]
Translation (o7)
[in: msg2, out: msg4]
ba1:
ba2:
(a) Original Process Plan P
Receive (o1)
[s1, out:msg1]
Assign (o8)
[in: msg3,msg4 out: msg5]
Invoke (o9)
[s3, in: msg5]
Assign (o2)
[in:msg1 out:msg2]
Invoke (o3)
[s2, in:msg2, out:msg3]
ba1:
Split (o-1)
[in:msg2 out:x1]
Merge (o-3)
[in:y1 out:msg4]
Iteration (o-2)
[foreach m in x1]
Switch (o4)
[in:x1]
Translation (o5)
[in: x1, out: y1]
Translation (o6)
[in: x1, out: y1]
Translation (o7)
[in: x1, out: y1]
ba2:
(b) Process Plan P
0
Figure 6: Example Rewriting of Process Plans.
MULTI-PROCESS OPTIMIZATION VIA HORIZONTAL MESSAGE QUEUE PARTITIONING
9

runs another message during ENQ() partitioning, its
counter c(m
i
) is increased by one. Serialization is
realized by timestamp comparison, and for each re-
ordered message, the counter is decreased by one.
Thus, at the outbound side, we are not allowed to send
message m
i
until c(m
i
) = 0. It can be shown that the
soft maximum latency constraint is still guaranteed.
6 EXPERIMENTAL EVALUATION
We provide selected results of our exhaustive exper-
imental evaluation. In general, the evaluation shows
that (1) significant throughput optimization is reach-
able and that (2) the maximum latency guarantees
hold under experimental investigation.
We implemented the approach of MPO via hor-
izontal partitioning within our java-based workflow
process engine (WFPE). This includes the partition
tree, slightly changed operators (partition-awareness)
and the algorithms for deriving partitioning attributes
(DPA), the rewriting of process plans (RPP), and the
automatic waiting time computation (WTC) as well
as the overall system integration in the sense of an en-
vironment for periodical re-optimization.
Subsequently, we ran our experiments on a blade
(OS Suse Linux, 32bit) with two processors (each of
them a Dual Core AMD Opteron Processor 270 at
1,994 MHz) and 8.9 GB RAM. With regard to re-
peatability, we used synthetically generated datasets.
As base integration process, we used our running
example (m = 5). To scale the number of opera-
tors m, we copied those operators and changed the
operator configurations slightly. The other scaling
factors were set to the following standard parame-
ters: number of messages |M
0
| = 100, message rate
R = 0.005
msg
ms
, selectivity according to the partition-
ing attribute sel = 0.1, batch size k
0
= 5, message rate
distribution function D = uni f orm, latency constraint
lc = 10s, maximum queue size qmax = 1, 000, and in-
put data size d = 1 (6kb messages). Finally, all exper-
iments were repeated 20 times.
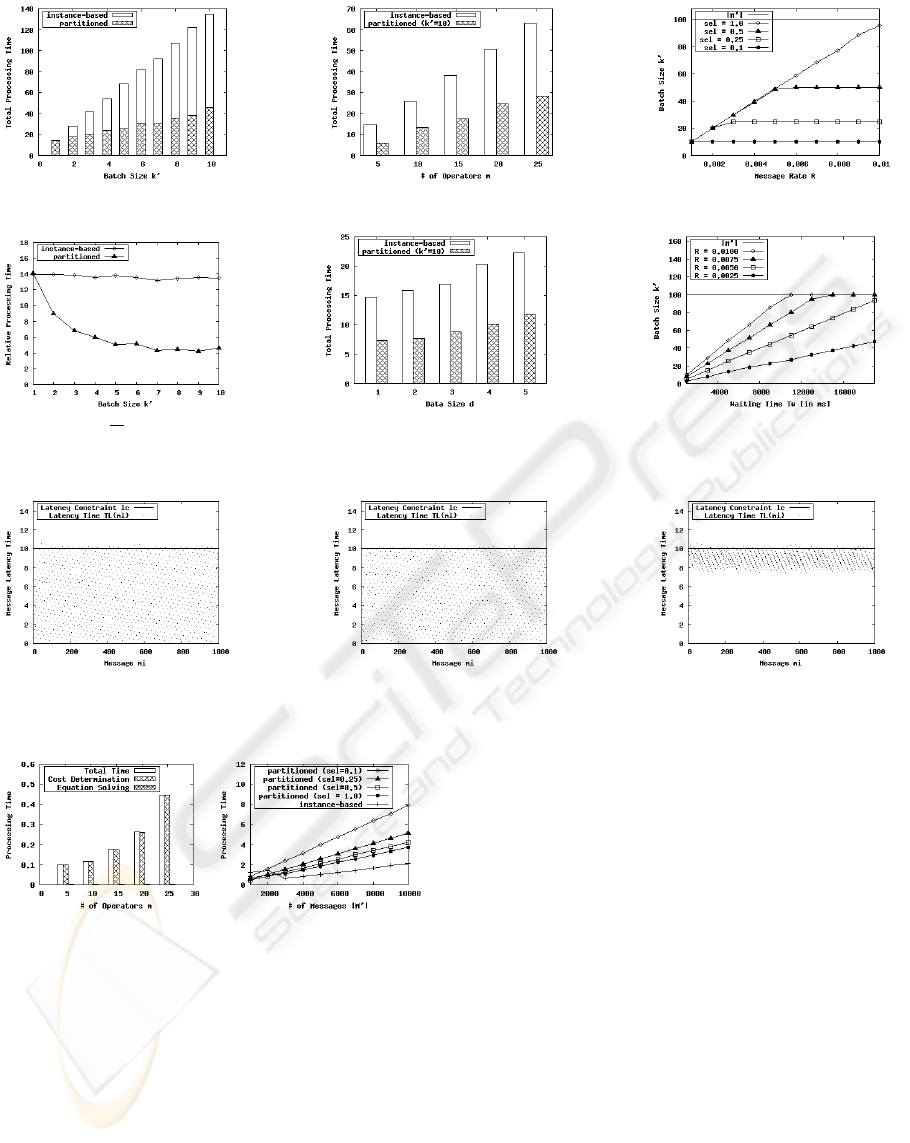
First, we investigated the processing time T
P
of
partitioned execution. Figure 7(a) shows the abso-
lute processing time of k
0
messages according to the
batch size k
0
. Instance-based execution means that
we executed one process instance for each message
of the batch as a baseline. Thus, the total processing
time linearly increases with increasing batch size. In
contrast, we only executed one process instance for
the complete batch when using MPO. Here, we can
observe that the total processing time increases log-
arithmically with increasing batch size. Then, Fig-
ure 7(d) shows the relative processing time of both ex-
ecution modes. For partitioned execution, we observe
that the relative processing time tends to the lower
bound (fraction of costs that linearly depends on the
batch size). The total message throughput directly de-
pends on this relative processing time (Little’s Law
(Little, 1961)). For the used process plan, we ob-
serve that partitioned execution improves the maxi-
mum throughput by a factor of three. Furthermore,
we fixed k
0
= 10 and varied the number of operators
m as well as the data size d. Figures 7(b) and 7(e)
illustrate the results of these scalability experiments,
where the relative improvement stays almost constant
when scaling both parameters.
Second, we evaluated the batch size k
0
according
to different message rates R (in
msg
ms
), selectivities sel,
and waiting times T
W
. We executed |M
0
| = 100 mes-
sages and fixed a waiting time of T
W
= 10s. Fig-
ure 7(c) shows the influence of the message rate R
on the maximum number of messages in the batch.
We can observe (1) that the higher the message rate,
the higher the number of messages in the batch, and
(2) that the selectivity determines the reachable upper
bound. However, the influence of the message rate
is independent of the selectivity (see Section 4). Fig-
ure 7(f) illustrates the influence of T
W
on k
0
, where we
fixed sel = 1.0. Note that both an increasing waiting
time as well as an increasing message rate increases
the batch size.
Third, we evaluated the latency influence of parti-
tioned process execution with regard to the maximum
latency guarantee. We executed |M
0
| = 1, 000 mes-
sages with a maximum latency constraint of lc = 10s
and measured the latency time T
L
(m
i
) of single mes-
sages m
i
. For both D = uni f orm (see Figure 8(a))
and D = poisson (see Figure 8(b))—this is typi-
cal for arrival processes of workflow instances (Xiao
et al., 2006)—the constraint is not significantly ex-
ceeded. However, in the latter case, peaks over the
latency constraint lc are possible. The constraint also
holds for serialized external behavior (SEB), where
all messages show more similar latency times (see
Figure 8(c), where D = uni f orm). This is due to seri-
alization at the outbound side. Thus, there is a lower
variance of single message latencies. Note that the la-
tency constraint is explicitly a soft constraint, where
we guarantee that it is not exceeded significantly. The
reason for this is that we compute the waiting time
based on our cost estimation. If the real execution
costs vary slightly around this estimate, there exist
cases where the constraint is slightly exceeded. Thus,
a hard latency constraint is impossible.
Fourth, we evaluated the algorithm overhead re-
quired for horizontally partitioned message execu-
tion. The runtime overhead—that includes the wait-
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
10
(a) Absolute T
P
(k
0
) [in ms] (b) Absolute T
P
(m) [in ms] (c) Batch Size k
0
(R)
(d) Relative
T
P
k
0
(k
0
) [in ms] (e) Absolute T
P
(d) [in ms] (f) Batch Size k
0
(T
W
)
Figure 7: Performance Benefit.
(a) Latency T
L
(uni f orm) (b) Latency T
L
(poisson) (c) Latency T
L
with SEB
Figure 8: Latency of Single Messages [in s].
(a) Computing T
W
(b) Enqueue M
0
Figure 9: Algorithm Runtime Overhead [in ms].
ing time computation (WTC, Figure 9(a)) and parti-
tioned queue maintenance (Figure 9(b))—is moder-
ate. Although WTC has a super-linear time com-
plexity, it took less than a millisecond for processes
with up to 25 operators. Furthermore, the partitioned
enqueue operation clearly depends on the selectiv-
ity. The lower the selectivity, the higher the over-
head. Anyway, the overhead to enqueue 10,000 mes-
sages (even for a selectivity of sel = 0.1) was only
six milliseconds compared to the standard message
queue. The deploy time overhead of partitioning in-
cludes the derivation of partitioning attributes (DPA)
and the rewriting of process plans (RPP). This over-
head is dominated by process plan parsing and un-
parsing. However, those efforts are required any-
way when analyzing and optimizing process plans
and they are required only once during deploy time.
Finally, we can state that MPO achieves signifi-
cant throughout improvement. How much we ben-
efit from MPO depends on the concrete workload.
The benefit is caused by two facts. First, even for
1-message partitions, there is only a moderate run-
time overhead (Figures 9(a) and 9(b)). Second, only
a small number of messages is required within one
partition to yield a significant speedup (Figure 7(d)).
7 RELATED WORK
Multi-Query Optimization. The basic concepts of
Multi-Query Optimization (MQO) (Roy et al., 2000)
are pipelined query execution and data sharing across
queries. Here, a huge body of work exists for lo-
MULTI-PROCESS OPTIMIZATION VIA HORIZONTAL MESSAGE QUEUE PARTITIONING
11

cal environments (Candea et al., 2009; Harizopou-
los et al., 2005; Johnson et al., 2007) as well as for
distributed query processing (Ives et al., 2004; Ke-
mentsietsidis et al., 2008; Lee et al., 2007; Unterbrun-
ner et al., 2009). For example, Lee et al. employed the
waiting opportunities within a blocking query execu-
tion plan (Lee et al., 2007). Further, Qiao et al. in-
vestigated a batch-sharing partitioning scheme (Qiao
et al., 2008) in order to allow similar queries to share
cache contents. The main difference between MPO
and MQO is that MQO benefits from the reuse of re-
sults across queries, while for MPO, this is impossi-
ble due to disjoint incoming messages. Further, MPO
handles dynamic data propagations and benefits from
redundant work and acceptable latency time. In addi-
tion, MPO computes the optimal waiting time.
Data Partitioning. Horizontal data (value-based)
partitioning (Ceri et al., 1982) is strongly applied in
DBMS. Typically, this is an issue of physical design
(Agrawal et al., 2004). However, there are more re-
cent approaches such as the table partitioning along
foreign-key constraints (Eadon et al., 2008). Further-
more, there are interesting approaches where data par-
titioning is used for distributed tables, such as Yahoo!
PNUTS (Silberstein et al., 2008) or Google BigTable
(Chang et al., 2006). In the area of data streams, data
partitioning was used in the sense of plan partitioning
across server nodes (Johnson et al., 2008) or single fil-
ter evaluation on tuple granularity (Avnur and Heller-
stein, 2000). Finally, there are similarities between
our horizontal partitioning approach and partitioning
in the area of parallel DBMS. The major difference is
that MPO handles infinite streams of messages.
Workflow Optimization. Though there is not much
work on optimizing integration processes, there is
a data-centric but rule-based approach to optimize
BPEL processes (Vrhovnik et al., 2007). In contrast,
we already proposed a cost-based optimization ap-
proach (Boehm et al., 2008). Anyway, it focuses on
execution time minimization rather than on through-
put maximization. Furthermore, there are existing
approaches (Biornstad et al., 2006; Boehm et al.,
2009; Li and Zhan, 2005; Srivastava et al., 2006) that
also address the throughput optimization. However,
those approaches try to increase the degree of par-
allelism, while our approach reduces executed work
across multiple instances of a process plan.
8 CONCLUSIONS
To summarize, we proposed a novel approach for
throughput maximization of integration processes that
reduces work by employing horizontal data partition-
ing. Our exhaustive evaluation showed that signifi-
cant performance improvements are possible and that
theoretical guarantees of optimality and latency also
hold under experimental investigation. In conclusion,
the MPO approach can seamlessly be applied in a
variety of different integration platforms that execute
asynchronous integration processes.
Further, the general MPO approach opens many
opportunities for further optimizations. Future work
might consider (1) the execution of partitions inde-
pendent of their temporal order, (2) process plan par-
titioning in the sense of compiling different plans for
different partitions, (3) global MPO for multiple pro-
cess plans, and (4) the cost-based process plan rewrit-
ing problem. Finally, it may be interesting (5) to com-
bine MPO with pipelining and load balancing because
both address throughput maximization as well.
REFERENCES
Agrawal, S., Narasayya, V. R., and Yang, B. (2004). Inte-
grating vertical and horizontal partitioning into auto-
mated physical database design. In SIGMOD.
Avnur, R. and Hellerstein, J. M. (2000). Eddies: Continu-
ously adaptive query processing. In SIGMOD.
Biornstad, B., Pautasso, C., and Alonso, G. (2006). Control
the flow: How to safely compose streaming services
into business processes. In SCC.
Boehm, M., Habich, D., Preissler, S., Lehner, W., and
Wloka, U. (2009). Cost-based vectorization of
instance-based integration processes. In ADBIS.
Boehm, M., Wloka, U., Habich, D., and Lehner, W.
(2008). Workload-based optimization of integration
processes. In CIKM.
Candea, G., Polyzotis, N., and Vingralek, R. (2009). A scal-
able, predictable join operator for highly concurrent
data warehouses. PVLDB, 2(1).
Cecchet, E., Candea, G., and Ailamaki, A. (2008).
Middleware-based database replication: the gaps be-
tween theory and practice. In SIGMOD.
Ceri, S., Negri, M., and Pelagatti, G. (1982). Horizontal
data partitioning in database design. In SIGMOD.
Chang, F., Dean, J., Ghemawat, S., Hsieh, W. C., Wallach,
D. A., Burrows, M., Chandra, T., Fikes, A., and Gru-
ber, R. (2006). Bigtable: A distributed storage system
for structured data. In OSDI.
Chaudhuri, S. and Shim, K. (1994). Including group-by in
query optimization. In VLDB.
Eadon, G., Chong, E. I., Shankar, S., Raghavan, A., Srini-
vasan, J., and Das, S. (2008). Supporting table parti-
tioning by reference in oracle. In SIGMOD.
Harizopoulos, S., Shkapenyuk, V., and Ailamaki, A. (2005).
Qpipe: A simultaneously pipelined relational query
engine. In SIGMOD.
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
12

Ivanova, M., Kersten, M. L., Nes, N. J., and Goncalves, R.
(2009). An architecture for recycling intermediates in
a column-store. In SIGMOD.
Ives, Z. G., Halevy, A. Y., and Weld, D. S. (2004). Adapt-
ing to source properties in processing data integration
queries. In SIGMOD.
Johnson, R., Hardavellas, N., Pandis, I., Mancheril, N.,
Harizopoulos, S., Sabirli, K., Ailamaki, A., and Fal-
safi, B. (2007). To share or not to share? In VLDB.
Johnson, T., Muthukrishnan, S. M., Shkapenyuk, V., and
Spatscheck, O. (2008). Query-aware partitioning for
monitoring massive network data streams. In SIG-
MOD.
Kementsietsidis, A., Neven, F., de Craen, D. V., and Van-
summeren, S. (2008). Scalable multi-query optimiza-
tion for exploratory queries over federated scientific
databases. In VLDB.
Lee, R., Zhou, M., and Liao, H. (2007). Request win-
dow: an approach to improve throughput of rdbms-
based data integration system by utilizing data sharing
across concurrent distributed queries. In VLDB.
Li, H. and Zhan, D. (2005). Workflow timed critical path
optimization. Nature and Science, 3(2).
Li, J., Tufte, K., Shkapenyuk, V., Papadimos, V., Johnson,
T., and Maier, D. (2008). Out-of-order processing:
a new architecture for high-performance stream sys-
tems. PVLDB, 1(1).
Little, J. D. C. (1961). A proof for the queueing formula:
l = λw. Operations Research, 9.
Qiao, L., Raman, V., Reiss, F., Haas, P. J., and Lohman,
G. M. (2008). Main-memory scan sharing for multi-
core cpus. PVLDB, 1(1).
Roy, P., Seshadri, S., Sudarshan, S., and Bhobe, S. (2000).
Efficient and extensible algorithms for multi query op-
timization. In SIGMOD.
Scheuermann, P. and Ouksel, A. M. (1982). Multidimen-
sional b-trees for associative searching in database
systems. Inf. Syst., 7(2).
Silberstein, A., Cooper, B. F., Srivastava, U., Vee, E., Yer-
neni, R., and Ramakrishnan, R. (2008). Efficient bulk
insertion into a distributed ordered table. In SIGMOD.
Srivastava, U., Munagala, K., Widom, J., and Motwani, R.
(2006). Query optimization over web services. In
VLDB.
Unterbrunner, P., Giannikis, G., Alonso, G., Fauser, D., and
Kossmann, D. (2009). Predictable performance for
unpredictable workloads. PVLDB, 2(1).
Vrhovnik, M., Schwarz, H., Suhre, O., Mitschang, B.,
Markl, V., Maier, A., and Kraft, T. (2007). An ap-
proach to optimize data processing in business pro-
cesses. In VLDB.
Xiao, Z., Chang, H., and Yi, Y. (2006). Optimal alloca-
tion of workflow resources with cost constraint. In
CSCWD.
APPENDIX
A FORMAL ANALYSIS
We additionally provide formal analysis results with
regard to the waiting time computation.
A.1 Optimality
First of all, we give an optimality guarantee for
T
P
(P
0
,k
0
) based on the computed waiting time.
Theorem 1. Optimality of Partitioned Execution:
The horizontal message queue partitioning solves
the MPO-P with optimality guarantees of T
P
(P
0
,k
0
) ·
|M
0
|
k
0
≤ T
P
(P
0
,k
0
−1) ·
|M
0
|
k
0
−1
≤ T
P
(P, 1) · k
0
, where k
0
> 1.
Proof. The processing time T
P
(P
0
,k
0
) is computed by
T
P
(P
0
,k
0
) = T
P
(P) ·
C(P
0
,k
0
)
C(P)
.
Further, the costs of a process plan C(P
0
,k
0
) are com-
posed of the costs C
+
(P
0
,k
0
) that linearly depend on
k
0
and costs C
−
(P
0
,k
0
) that sub-linearly depend on k
0
,
with C(P
0
,k
0
) = C
+
(P
0
,k
0
) + C
−
(P
0
,k
0
). In conclu-
sion, in the worst case, the processing time T
P
(P
0
,k
0
)
increases linearly when increasing k
0
. Thus, the rela-
tive processing time
T
P
(P
0
,k
0
)
k
0
is a monotonically non-
increasing function with
k
0
,k
00
∈ [1,|M
0
|] : k
0
< k
00
⇒
T
P
(P
0
,k
0
)
k
0
≥
T
P
(P
0
,k
00
)
k
00
.
If we now fix a certain |M
0
|, it follows directly that
T
P
(P
0
,k
0
) ·
|M
0
|
k
0
≤ T
P
(P
0
,k
0
− 1) ·
|M
0
|
k
0
− 1
≤ T
P
(P,1) · k
0
.
Hence, Theorem 1 holds.
A.2 Latency Constraint
Furthermore, we guarantee to preserve the given max-
imum latency constraint for individual messages.
Theorem 2. Soft Guarantee of Maximum Latency:
The waiting time computation ensures that—for a
given message rate R, with D = uni f orm—the latency
time of a single message T
L
(m
i
) with m
i
∈ M
0
will not
significantly exceed the maximum latency constraint
lc with T
L
(m
i
) ≤ lc.
Proof. In the worst case,
1
sel
distinct messages m
i
ar-
rive simultaneously in the system. Hence, the high-
est possible latency time T
L
(m
i
) is given by
1
sel
· T
W
+
T
P
(P
0
,k
0
). Due to our validity condition of
ˆ
T
L
≤ lc,
we need to show that T
L
(m
i
) ≤
ˆ
T
L
even for this worst
case. Further, our validity condition ensures that T
W
≥
T
P
(P
0
,k
0
). Thus, we can write T
L
(m
i
) ≤
ˆ
T
L
(T
W
,R) as
MULTI-PROCESS OPTIMIZATION VIA HORIZONTAL MESSAGE QUEUE PARTITIONING
13

1
sel
· T
W
+ T
P
(P
0
,k
0
) ≤
|M
0
|
k
0
· T
W
+ T
P
(P
0
,k
0
)
1
sel
· T
W
≤
|M
0
|
k
0
· T
W
.
We substitute T
W
with
k
0
R
and subsequently substitute
|M
0
| by
k
0
sel
(the cardinality |M
0
| is equal to the number
of partitions
1
sel
times the cardinality of a partition k
0
),
and we get
k
0
R · sel
≤
|M
0
|
R
=
k
0
R · sel
.
Thus, for the worst case, T
L
(m
i
) = lc (more specific,
T
L
(m
|M
0
|
) = lc), while for all other cases, T
L
(m
i
) ≤ lc
is true. Hence, Theorem 2 holds.
Note that by hypothesis testing, it can be shown
that this guarantee of maximum latency also holds for
arbitrary probability distributions of the message rate.
A.3 Lower Bound of Relative Costs
In analogy to Amdahl’s law, where the fraction of a
task (processing time) that cannot be executed in par-
allel determines the upper bound for the reachable
speedup, we compute the lower bound of the rela-
tive processing costs. The existence of this lower
bound was empirically shown in Section 6. There-
fore, let T
P
(P
0
,k
0
) denote the absolute processing time
using batches of k
0
messages. Let C(P) denote the
costs for k
0
= 1; C
+
(P) denotes the costs that linearly
depend on k
0
, and C
−
(P) denotes the costs that de-
pend sub-linearly on k
0
. Here, the condition C(P) =
C
+
(P) + C
−
(P) holds. Finally,
T
P
(P
0
,k
0
)
k
0
denotes the
relative processing time at k
0
. This relative processing
time asymptotically tends to a lower bound.
Theorem 3. The lower bound of relative processing
costs
T
P
(P
0
,k
0
)
k
0
is given by T
P
(P) ·
C
+
(P)
C(P)
as the fraction
of costs that linearly depend on k
0
and of the instance-
based costs.
Proof. Recall that—according to Equation 3—the ab-
solute processing time T
P
(P
0
,k
0
) is computed by
T
P
(P
0
,k
0
) = T
P
(P)·
C(P
0
,k
0
)
C(P)
= T
P
(P)·
C
+
(P
0
,k
0
) +C
−
(P
0
,k
0
)
C(P)
.
Due to the linear dependency of C
+
(P
0
,k
0
) on k
0
, we
can now write C
+
(P
0
,k
0
) = C
+
(P
0
,1)· k
0
= C
+
(P)·k
0
.
Further, C
−
(P
0
,k
0
) has a sub-linear dependency on k
0
by definition. If we now let k
0
tend to ∞ with
T
P
(P
0
,k
0
)
k
0
= T
P
(P) ·
C
+
(P) · k
0
C(P) · k
0
+
C
−
(P
0
,k
0
)
C(P) · k
0
lim
k
0
→∞
T
P
(P
0
,k
0
)
k
0
= T
P
(P) ·
C
+
(P)
C(P)
,
we see that
T
P
(P
0
,k
0
)
k
0
asymptotically tends to T
P
(P) ·
C
+
(P)
C(P)
. Hence, Theorem 3 holds.
A.4 Serialized External Behavior
According to the requirement of serialized external
behavior, we might need to serialize messages at the
outbound side. Therefore, we extended the message
structure by a counter c with c ∈ N to a (t
i
,c
i
,d
i
)-
tuple. If a message m
i
outruns another message dur-
ing ENQ() partitioning, its counter c(m
i
) is increased
by one. The serialization is realized by timestamp
comparison, and for each reordered message, the
counter is decreased by one. Thus, at the outbound
side, we are not allowed to send message m
i
until its
counter is c(m
i
) = 0.
Theorem 4. Serialized Behavior: The Soft Guarantee
of Maximum Latency theorem also holds in the case
that we have to preserve the serial order of external
behavior.
Proof. Basically, we need to prove that the condition
T
L
(m
i
) ≤
ˆ
T
L
≤ lc is true even if we have to serialize
the external behavior. Therefore, recall the worst case
(Theorem 2), where the latency time is given by
T
L
(m
i
) =
1
sel
· T
W
+ T
P
(P
0
,k
0
).
Here, the message m
i
has not outrun any other mes-
sages. Thus, there is no serialization time required.
For all other messages that exhibit a general latency
time of
T
L
(m
i
) =
1
sel
− x
· T
W
+ T
∗
P
(P
0
,k
0
),
where x denotes the number of partitions after the par-
tition of m
i
, this message has outrun at most x·k
0
mes-
sages and its partition is executed in T
∗
P
(P
0
,k
0
). Thus,
additional serialization time of x · T
W
+ T
P
(P
0
,k
0
) is
needed. In conclusion, we get
T
L
(m
i
) =
1
sel
− x
· T
W
+ T
∗
P
(P
0
,k
0
) //normal latency
+ x · T
W
+ T
P
(P
0
,k
0
) //serialization
=
1
sel
· T
W
+ T
P
(P
0
,k
0
).
Thus, T
L
(m
i
) ≤
ˆ
T
L
≤ lc is true for the serialized case
as well because T
∗
P
(P
0
,k
0
) is subsumed by x · T
W
be-
cause the waiting time is longer than the processing
time due to the validity condition of T
W
≥ T
P
. Hence,
Theorem 4 holds.
Counting messages that have been outrun also
works for CN:CM multiplicities between input and
output messages
1
. In fact, the proof works only for
sequences of operators.
1
Messages with counters not equal to zero are ousted
by subsequent messages with higher timestamps, and the
outbound queues are periodically flushed.
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
14
