
IMPROVEMENT OF DIFFERENTIAL CRISP CLUSTERING USING
ANN CLASSIFIER FOR UNSUPERVISED PIXEL
CLASSIFICATION OF SATELLITE IMAGE
Indrajit Saha, Dariusz Plewczynski
ICM, University of Warsaw, 02-089 Warsaw, Poland
Ujjwal Maulik
Department of Computer Science and Engineering, Jadavpur University, Kolkata-700032, West Bengal, India
Sanghamitra Bandyopadhyay
Machine Intelligence Unit, Indian Statistical Institute, Kolkata-700108, West Bengal, India
Keywords:
ANN classifier, Crisp clustering, Differential evolution, Statistical significance test, IRS satellite image.
Abstract:
An important approach to unsupervised pixel classification in remote sensing satellite imagery is to use clus-
tering in the spectral domain. In particular, satellite images contain landcover types some of which cover
significantly large areas, while some (e.g., bridges and roads) occupy relatively much smaller regions. De-
tecting regions or clusters of such widely varying sizes presents a challenging task. This fact motivated us to
present a novel approach that integrates a differential evaluation based crisp clustering scheme with artificial
neural networks (ANN) based probabilistic classifier to yield better performance. Real-coded encoding of the
cluster centres is used for the differential evaluation based crisp clustering. The clustered solution is then used
to find some points based on their proximity to the respective centres. The ANN classifier is thereafter trained
by these points. Finally, the remaining points are classified using the trained classifier. Results demonstrating
the effectiveness of the proposed technique are provided for several synthetic and real life data sets. Also sta-
tistical significance test has been performed to establish the superiority of the proposed technique. Moreover,
one remotely sensed image of Bombay city has been classified using the proposed technique to establish its
utility.
1 INTRODUCTION
For remote sensing applications, classification is an
important task which partitions the pixels in the im-
ages into homogeneous regions, each of which corre-
sponds to some particular landcover type. The prob-
lem of pixel classification is often posed as clustering
in the intensity space. In a satellite image, each pixel
represents a landcover area, which may not necessar-
ily belong to a single landcover type. Thus in remote
sensing images, large number of pixels may have sig-
nificant belongingness to multiple classes. There-
fore a large amount of uncertainty is associated with
the pixels in a remotely sensed image. In the unsu-
pervised pixel classification framework, various clus-
tering algorithms like K-means (Everitt, 1993; Jain
et al., 1999), split-and-merge (Laprade, 1988) and
scale space techniques (Wong and Posner, 1993) have
been used for the purpose of satellite image segmen-
tation.
Clustering (Jain and Dubes, 1988) is a useful unsu-
pervised data mining technique which partitions the
input space into K regions depending on some simi-
larity/dissimilarity metric where the value of K may
or may not be known a priori. K-means (Jain et al.,
1999) is a traditional partitional clustering algorithm
which starts with K random cluster centroids and the
centroids are updated in successive iterations by com-
puting the numerical averages of the feature vectors in
each cluster. The objective of the K-means algorithm
is to maximize the global compactness of the clusters.
The main disadvantages of the K-means clustering al-
21
Saha I., Plewczynski D., Maulik U. and Bandyopadhyay S. (2010).
IMPROVEMENT OF DIFFERENTIAL CRISP CLUSTERING USING ANN CLASSIFIER FOR UNSUPERVISED PIXEL CLASSIFICATION OF
SATELLITE IMAGE.
In Proceedings of the 12th International Conference on Enterprise Information Systems - Artificial Intelligence and Decision Support Systems, pages
21-29
DOI: 10.5220/0002872800210029
Copyright
c
SciTePress

gorithm are (1) it depends much on the initial choice
of the modes and (2) it often gets trapped into some
local optimum. However, these facts are motivated us
to provide a new crisp clustering technique and it’s
improvement using supervised classifier.
In 1995 a new floating point encoded evolutionary
algorithm for global optimization called Differential
Evolution (DE) was proposed in (Storn and Price,
1997) that uses a special kind of differential opera-
tor. Recently, DE has been found a wide spread ap-
plication in different fields of engineering and sci-
ence. Also by carrying this fact, we are propos-
ing a integrated approach with differential evaluation
based crisp clustering (DECC) and ANN classifier
(Bishop, 1996; MacKay, 1992). The differential eval-
uation based crisp clustering technique is used to find
the proper partitions and after that, the ANN clas-
sifier is trained by fraction of data points, selected
based on their proximity to the respective centres. Fi-
nally, remaining points are classified by trained clas-
sifier. The efficiency of the proposed technique is
compared with genetic algorithm based crisp cluster-
ing (GACC), simulated annealing based crisp clus-
tering (SAFC) and well-known K-mean (Jain et al.,
1999) algorithm. However, it’s integrated version like
GACC-ANN, SACC-ANN and K-means-ANN has
also been tested. Effectiveness of this proposed tech-
nique has been established by quantitatively, visually
and statistically. Moreover, Different landcover re-
gions in remote sensing imagery have also been clas-
sified using the proposed technique.
2 CRISP CLUSTERING
ALGORITHMS
2.1 K-means
The K-means algorithm (Jain et al., 1999), one of the
most widely used ones, attempts to solve the cluster-
ing problem by optimizing a given metric. The objec-
tive to minimize the within cluster variance ζ.
ζ =
K
∑
i=1
∑
x∈C
i
D(x, m
i
) (1)
Here m
i
is the mean of clusterC
i
and D(x, m
i
) denotes
the distance between the point x and m
i
. K denotes
the number of clusters. The resulting clustering of the
data set X is usually only a local minimum of ζ. The
idea in K-means is to select K representativepoints as
a centre, in X and assign the rest of the data points to
the cluster identified by the nearest. Initial set of K
centres are selected randomly. Subsequently, all the
points in X are assigned to the nearest centre. In each
iteration, a new mean is determined for each cluster.
After that, all the points in X are reassigned to their
clusters in accordance with the new set of centre or
mean. The algorithm iterates until ζ does not change
any more.
2.2 Genetic Algorithm based Crisp
Clustering
In Genetic Algorithm (Goldberg, 1989) based Crisp
Clustering (GACC), the chromosomes are made up of
real numbers which represent the coordinates of the
centres of the partitions. If chromosome i encodes the
centres of K clusters in d dimensional space then its
length l is d × K. For initializing a chromosome, the
K centres are randomly selected points from the data
set while ensuring that they are distinct. The fitness
of a chromosome indicates the degree of goodness of
the solution it represents. In this article, ζ is used for
this purpose. The objective is therefore to minimize
ζ for achieving proper clustering. Given a chromo-
some, the centres encoded in it are first extracted. Let
the chromosome encode K centres, and let these be
denoted as z
1
, z
2
, . . . , z
K
. The centres encoded in a
chromosome are updated new set of centres or mean.
Conventional proportional selection implemented by
the roulette wheel strategy is applied on the popula-
tion of strings. The standard single point crossover is
applied stochastically with probability µ
c
. The clus-
ter centres are considered to be indivisible, i.e., the
crossover points can only lie in between two clusters
centres. In each gene position of a chromosome is
subjected to mutation with a fixed probability µ
m
, re-
sulting in the overall perturbation of the chromosome.
A number ± in the range [0, 1] is generated with uni-
form distribution. If the value at a gene position is v,
after mutation it becomes (1±2×δ)×v, when v 6= 0,
and ±2×δ, when v = 0. The ’+’ or ’-’ sign occurs
with equal probability. Note that, because of muta-
tion more than one cluster centre may be perturbed in
a chromosome. The algorithm is termination after it
has executed a fixed number of generations. The eli-
tist model of GAs has been used, where the best string
seen so far is stored in a location within the popula-
tion. The best string of the last generation provides
the solution to the clustering problem. Fig. 1 demon-
strate the GACC algorithm.
2.3 Simulated Annealing based Crisp
Clustering
Simulated annealing (SA) (Kirkpatrik et al., 1983;
van Laarhoven and Aarts, 1987) is an optimization
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
22
Initial Population.
(Here each chromosome encodes real value of corre-
sponding to K centres)
Fitness computation using ζ. (see Eqn. (1))
Repeat
Roulette Wheel Selection.
Crossover.
Mutation.
Fitness Computation.
Until (termination criteria are met)
Figure 1: GACC Algorithm.
tool which has successful applications in a wide range
of combinatorial as well as functional optimization
problems. The fact motivated researchers to use a SA
to optimize the clustering problem where it provides
near optimal solutions of an objective or fitness func-
tion in complex, large and multimodal landscapes. In
Simulated Annealing based Crisp Clustering (SACC)
a string or configuration encodes d × K cluster cen-
tres. Subsequently the string is updated using the new
centres, computed as a mean. Thereafter the energy
function, ζ, is computed as per Eqn. (1). The cur-
rent string is perturbed using the mutation operation
as discussed for GACC. This way, perturbation of a
string yields a new string. It’s energy is also computed
in a similar fashion. If the energy of the new string
(E(s)) is less than that of the current string (E(p)), the
new string is accepted. Otherwise the newstring is ac-
cepted based on a probability
exp(−(E(s)−E(p)))
T
where
T is the current temperature of the SA process. Fig. 2
describes the SACC algorithm in detail.
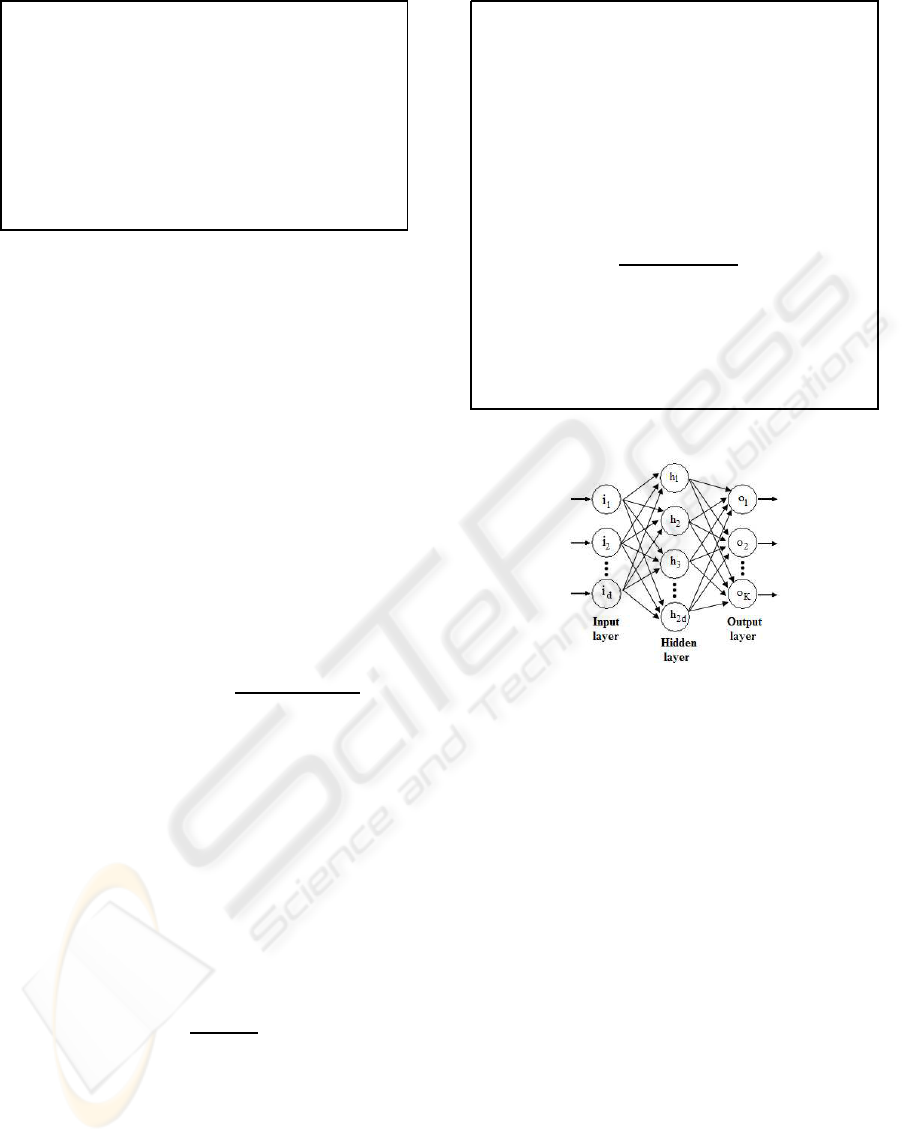
3 ANN BASED CLASSIFIER
The ANN classifier (Fig. 3) algorithm used in this
article implements a three layer feed-forward neu-
ral network with a hyperbolic tangent function for
the hidden layer and the softmax function (Andersen
et al., 1997) for the out put layer. Using softmax, out-
put of ith output neuron is given by:
P
i
=
e
q
i
∑
K
j=1
e
q
j
(2)
where q
i
the net input to the ith output neuron, and K
is the number of output neurons. The use of softmax
makes it possible to interpret the outputs as probabil-
ities. The number of neurons in the input layer is d,
where d is the number of features of the input data
set. The number of neurons in the output layer is
K, where K is the number of classes. The ith out-
put neuron provides the class membership degree of
p = Random initial configuration.
(Here each chromosome encodes real value of corre-
sponding to K centres)
T = T
max
.
E(p) = Energy of p is computed using Eqn. (1).
while( T ≥ T
min
)
for i = 1 to k
s = Perturb ( p ).
E(s) = Energy of s is computed using Eqn. (1).
if (E(s) - E(p) < 0 )
Set p = s and E(p) = E(s)
else
if (rand(0,1) <
exp(−(E(s)−E(p)))
T
)
Set p = s and E(p) = E(s)
end if
end if
end for
T= T×r. /* 0 < r < 1 */
end while
Figure 2: SACC Algorithm.
Figure 3: Three layer feed-forward ANN classifier model.
the input pattern to the ith class. The number of hid-
den layer neurons is taken as 2× d. The weights are
optimized with a maximum a posteriori (MAP) ap-
proach; cross-entropy error function augmented with
a Gaussian prior over the weights. The regularization
is determined by MacKay’s ML-II scheme (MacKay,
1992). Outlier probability of training examples is also
estimated (Sigurdsson et al., 2002). Fig. 3 shows the
feed-forward ANN classifier model.
4 PROPOSED TECHNIQUE
4.1 Differential Evolution based Crisp
Clustering
Differential Evolution (Storn and Price, 1995; Storn
and Price, 1997) is a relatively recent heuristic de-
signed to optimize problems over continuous do-
mains. In DECC, Each vector is a sequence of real
numbers representing the K cluster centres. For an d-
dimensional space, the length of a vector is l = d × K,
IMPROVEMENT OF DIFFERENTIAL CRISP CLUSTERING USING ANN CLASSIFIER FOR UNSUPERVISED
PIXEL CLASSIFICATION OF SATELLITE IMAGE
23

where the first d positions represent the first cluster
centre, the next d positions represent those of the sec-
ond cluster centre, and so on. The K cluster centres
encoded in each vector are initialized to K randomly
chosen points from the data set. This process is re-
peated for each of the P vectors in the population,
where P is the size of the population. The kth individ-
ual vector of the population at time-step (generation)
t has l components (d × K), i.e.,
G
k
(t) = [G
k,1
(t), G
k,2
(t), . . . , G
k,l
(t)] (3)
For each target vector G
k
(t) that belongs to the cur-
rent population, three randomly selected vectors from
the current population is used. In other words the lth
component of each trial offspring is generated as fol-
lows.
ϑ
k
(t + 1) = G
i
(t) + F (G
n
(t) − G
m
(t)) (4)
Here F is a mutation factor. In order to increase
the diversity of the perturbed parameter vectors,
crossover is introduced. To this end, the trial vector:
Q
k
(t + 1) = [Q
k,1
(t + 1), Q
k,2
(t + 1), . . . , Q
k,l
(t + 1)]
(5)
is formed, where
Q
jk
(t+1) =
ϑ
jk
(t + 1)
if rand
j
(0, 1) ≤ CR or j = rand(k)
G
k
(t)
if rand
j
(0, 1) > CR and j 6= rand(k)
(6)
In Eqn. (6), rand
j
(0, 1) is the jth evaluation of a uni-
form random number generator with outcome ∈ [0,
1]. CR is the crossover rate ∈ [0, 1] which has to be
determined by the user. rand(k) is a randomly chosen
index ∈ {1, 2,. . .,d} which ensures that Q
k
(t + 1) gets
at least one parameter from ϑ
k
(t + 1). The following
condition decide whether or not it should become a
member of next generation (t + 1),
G
k
(t + 1) =
Q
k
(t + 1)
if f(Q
k
(t + 1)) > f(G
k
)
G
k
(t)
if f(Q
k
(t + 1)) ≤ f(G
k
)
(7)
where f(.) is the objective function to be minimized
in this article. The processes of mutation, crossover
and selection are executed for a fixed number of iter-
ations. The best vector seen up to the last generation
provides the solution to the clustering problem.
4.2 Integration with ANN Classifier
Step1: After execution of DECC or GACC or SACC
or K-means to obtain a best solution vector
consisting of cluster centres.
Step2: Select 50% of data points from each clus-
ter which are nearest to the respective cluster
centres. The class labels of the points are set
to the respective cluster number.
Step3: Train a ANN classifier with the points se-
lected in step 2.
Step4: Generate the class labels for the remaining
points using the trained ANN classifier.
5 EXPERIMENTAL RESULTS
5.1 Artificial Data Sets
Data1: This is an overlapping two dimensional data
set where the number of clusters is five. It has 250
points. The value of K is chosen to be 5. The data set
is shown in Fig. 4.a.
Data2: This is also a two dimensional data set con-
sisting of 900 points. The data set has 9 classes. The
data set is shown in Fig. 4.b.
4 6 8 10 12 14 16
4
6
8
10
12
14
16
−4 −3 −2 −1 0 1 2 3 4
−4
−3
−2
−1
0
1
2
3
4
(a) (b)
Figure 4: Two Artificial Data Set (a) and (b).
5.2 Real-life Data Sets
Iris: This data consists of 150 patterns divided into
three classes of Iris flowers namely, Setosa, Virginia
and Versicolor. The data is in four dimensional space
(sepal length, sepal width, petal length and petal
width).
Cancer: It has 683 patterns in nine features (clump
thickness, cell size uniformity, cell shape uniformity,
marginal adhesion, single epithelial cell size, bare nu-
clei, bland chromatin, normal nucleoli and mitoses),
and two classes malignant and benign. The two
classes are known to be linearly inseparable.
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
24

5.3 Performance Metrics
5.3.1 Minkowski Score
The performances of the clustering algorithms are
evaluated in terms of the Minkowski Score (MS) (Jar-
dine and Sibson, 1971). This is a measure of the qual-
ity of a solution given the true clustering. Let T be
the “true” solution and S the solution we wish to mea-
sure. Denote by n
11
the number of pairs of elements
that are in the same cluster in both S and T. Denote
by n
01
the number of pairs that are in the same cluster
only in S, and by n
10
the number of pairs that are in
the same cluster in T. Minkowski Score (MS) is then
defined as:
MS =
r
n
01
+ n
10
n
11
+ n
10
(8)
For MS, the optimum score is 0, with lower scores
being “better”.
5.4 Input Parameters
The population size and number of generation used
for DECC and GACC are 50 and 100 respectively.
The crossoverprobability and mutation factors (F) for
DECC are set to be 0.8 and 0.7, respectively. The
crossover and mutation probabilities for GACC are
taken to be 0.8 and 0.3, respectively. The parame-
ters of the SA based fuzzy clustering algorithm are as
follows: T
max
=100, T
min
=0.01, r=0.9 and k=100. The
K-means algorithm is executed till it converges to the
final solution. For all the fuzzy clustering algorithms
m, the fuzzy exponent, is set to 2.0. Results reported
in the tables are the average values obtained over 50
runs of the algorithms. Note that the input parame-
ters used here are fixed either following the literature
or experimentally. For example the value of fuzzy
exponent (m), the scheduling of simulated annealing
follows the literature whereas the crossover, mutation
probability, population size, number of generation is
fixed experimentally.
5.5 Performance
Tables 1 to 2 report the average values of ζ and
MS indices provided by DECC-ANN, GACC-ANN,
SACC-ANN, K-means-ANN, DECC, GACC, SACC
and K-means clustering over 50 runs of the algo-
rithms for the two synthetic and two real life data
sets considered here. The values reported in the
tables show that for all the data sets, DECC-ANN
provides the best ζ and MS indices score. For ex-
ample, Cancer data set, the average value of MS
produces by DECC-ANN algorithm is 0.3511. The
MS value produce by GACC-ANN, SACC-ANN, K-
means-ANN, DECC, GACC, SACC and K-means are
0.3702, 0.3873, 0.4502, 0.3733, 0.3839, 3945 and
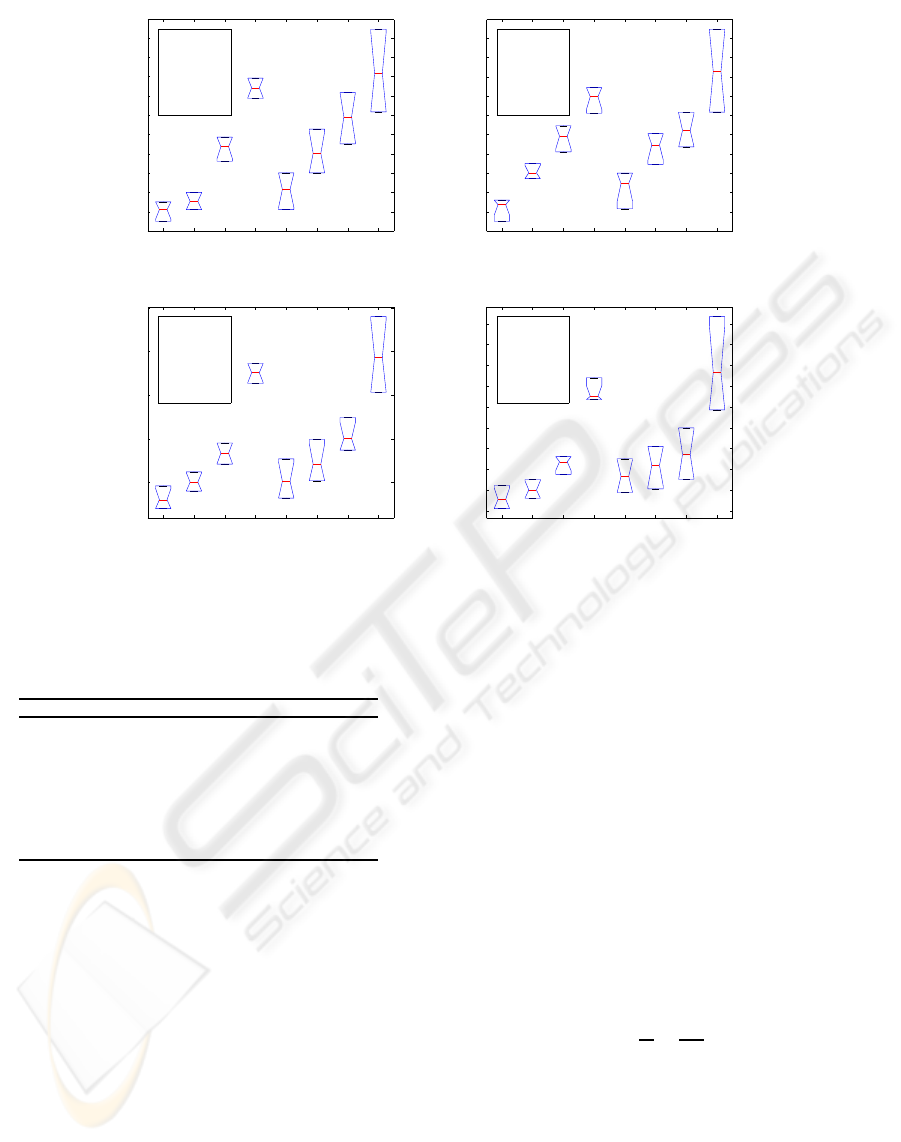
0.4733, respectively. Fig. 5 demonstrates the box-
plot as well as the convergence plot of different al-
gorithms. As can be seen from the figures the perfor-
mance of the proposed DECC-ANN is the best for all
the data sets.
Table 1: Average ζ and MS values over 50 runs of different
algorithms for the two Artificial data sets.
Algorithms Data1 Data1
ζ MS ζ MS
DECC-ANN 486.17 0.3022 467.33 0.4074
GACC-ANN 488.34 0.3108 470.62 0.4404
SACC-ANN 490.71 0.3673 475.53 0.4784
K-means-ANN 496.72 0.4283 481.64 0.5194
DECC 488.02 0.3231 469.05 0.4293
GACC 489.16 0.3604 472.5 0.4694
SACC 494.65 0.3982 477.47 0.4844
K-means 498.36 0.4433 484.88 0.5454
Table 2: Average ζ and MS values over 50 runs of different
algorithms for the two Real-life data sets.
Algorithms Iris Cancer
ζ MS ζ MS
DECC-ANN 75.05 0.3803 19324.13 0.3511
GACC-ANN 77.62 0.4004 19327.04 0.3702
SACC-ANN 80.72 0.4336 193330.62 0.3873
K-means-ANN 83.07 0.5257 19336.82 0.4502
DECC 78.93 0.4013 19327.54 0.3733
GACC 79.83 0.4210 19329.02 0.3839
SACC 82.62 0.4502 19332.42 0.3945
K-means 85.42 0.5434 19339.82 0.4733
5.6 Statistical Significance Test
A non-parametric statistical significance test called
Wilcoxons rank sum test (Hollander and Wolfe, 1999)
for independent samples has been conducted at the
5% significance level. Eight groups, corresponding
to the eight algorithms (1. DECC-ANN, 2. GACC-
ANN, 3. SACC-ANN, 4. K-means-ANN, 5. DECC,
6. GACC, 7. SACC, 8. K-means), have been created
for each data set. Each group consists of the MS for
the data sets produced by 50 consecutive runs of the
corresponding algorithm. The median values of each
group for all the data sets are shown in Table 3.
It is evident from Table 3 that the median values
for DECC-ANN are better than that for other algo-
rithms. To establish that this goodness is statisti-
cally significant, Table 4 reports the p-values pro-
duced by Wilcoxons rank sum test for comparison
of two groups (one group corresponding to DECC-
ANN and another group corresponding to some other
algorithm) at a time. As a null hypothesis, it is as-
sumed that there is no significant difference between
the median values of two groups. Whereas, according
to the alternative hypothesis there is significant differ-
IMPROVEMENT OF DIFFERENTIAL CRISP CLUSTERING USING ANN CLASSIFIER FOR UNSUPERVISED
PIXEL CLASSIFICATION OF SATELLITE IMAGE
25
1 2 3 4 5 6 7 8
0.3
0.32
0.34
0.36
0.38
0.4
0.42
0.44
0.46
0.48
Minkowski Score
Different Algorithms
1−>DECC−ANN
2−>GACC−ANN
3−>SACC−ANN
4−>K−means−ANN
5−>DECC
6−>GACC
7−>SACC
8−>K−means
1 2 3 4 5 6 7 8
0.4
0.42
0.44
0.46
0.48
0.5
0.52
0.54
0.56
0.58
Minkowski Score
Different Algorithms
1−>DECC−ANN
2−>GACC−ANN
3−>SACC−ANN
4−>K−means−ANN
5−>DECC
6−>GACC
7−>SACC
8−>K−means
(a) (b)
1 2 3 4 5 6 7 8
0.4
0.45
0.5
0.55
0.6
Minkowski Score
Different Algorithms
1−>DECC−ANN
2−>GACC−ANN
3−>SACC−ANN
4−>K−means−ANN
5−>DECC
6−>GACC
7−>SACC
8−>K−means
1 2 3 4 5 6 7 8
0.34
0.36
0.38
0.4
0.42
0.44
0.46
0.48
0.5
0.52
Minkowski Score
Different Algorithms
1−>DECC−ANN
2−>GACC−ANN
3−>SACC−ANN
4−>K−means−ANN
5−>DECC
6−>GACC
7−>SACC
8−>K−means
(c) (d)
Figure 5: Boxplot of MS for different clustering algorithms for (a) Data1, (b) Data2, (c) Iris and (d) Cancer data sets.
Table 3: Median values of the Minkowski Scores for the
Data sets over 50 consecutive runs of different algorithms.
Algorithm Data1 Data2 Iris Cancer
DECC-ANN 0.2946 0.4122 0.3982 0.3483
GACC-ANN 0.3203 0.4582 0.4144 0.3872
SACC-ANN 0.3503 0.4673 0.4283 0.3953
K-means-ANN 0.4377 0.5244 0.5382 0.4483
DECC 0.3352 0.4261 0.4102 0.3672
GACC 0.3572 0.4577 0.4601 0.3903
SACC 0.3862 0.4902 04682 0.4035
K-means 0.4521 0.5563 0.5482 0.4837
ence in the median values of the two groups. All the
p-values reported in the table are less than 0.05 (5%
significance level). For example, the rank sum test
between the algorithms DECC-ANN and GACC for
Iris provides a p-value of 1.3253e-004, which is very
small. This is strong evidence against the null hypoth-
esis, indicating that the better median values of the
performance metrics produced by DECC-ANN is sta-
tistically significant and has not occurred by chance.
Similar results are obtained for all other data sets and
for all other algorithms compared to DECC-ANN, es-
tablishing the significant superiority of the proposed
technique.
6 APPLICATION TO SATELLITE
IMAGE SEGMENTATION
In this section, an IRS remote sensing satellite im-
age of a part of the city of Bombay has been used for
demonstrating unsupervised pixel classification. The
results obtained by application of DECC-ANN clus-
tering have been reported and compared with other
stated clustering algorithms. The results are shown
both graphically and numerically. To show the effec-
tiveness of the DECC-ANN technique, a cluster va-
lidity index I (Maulik and Bandyopadhyay,2002) has
been examined. The index I , proposed recently as a
measure of indicating the goodness/validity of cluster
solution, is defined as follows:
I (K) = (
1
K
×
E
1
E
K
× D
K
)
p
, (9)
where K is the number of clusters. Here,
E
K
=
K
∑
k=1
n
∑
i=1
u
k,i
k z
k
− x
i
k, (10)
and
D
K
= max
k6= j
k z
k
− z
j
k, (11)
In this article, we have taken p = 2. Here u
k,i
is the
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
26

Table 4: P− values produced by Wilcoxon’s Rank Sum test comparing with DECC-ANN with other algorithms.
DataSet P-value
GACC-ANN SACC-ANN K-means-ANN DECC GACC SACC K-means
Data1 0.0302 2.0361e-003 1.4077e-004 0.0125 1.6327e-004 3.8224e-004 5.3075e-005
Data2 0.0313 2.8531e-003 .2934e-004 0.0173 1.3253e-004 4.0504e-004 4.9177e-005
Iris 0.03150 3.6603e-003 2086e-004 0.0162 1.3253e-004 3.9204e-004 4.8177e-005
Cancer 0.031 2.0462e-003 1.2086e-004 0.0147 1.3586e-004 4.3858e-004 4.9177e-005
City
Area
Islands
The
Dockyard
Island
The
Arabian
Sea
Figure 6: IRS image of Bombay in the NIR band with his-
togram equalization.
membership of pattern x
i
to the kth cluster. For crisp
clustering u
k,i
will be 0 or 1. Larger value of I index
implies better solution.
Note that for computing the Minkowski score, knowl-
edge about the true partitioning of the data is neces-
sary. This knowledge is not available for the pixel
classification problem considered here. Therefore, the
Minkowski Score can not be used for evaluating clus-
tering performance in this case. Hence the internal
clustering criterion I index is used for performance
comparison. Larger value of I index implies a better
solution.
6.1 IRS Image of Bombay
The data used here was acquired from the Indian
Remote Sensing Satellite (IRS-1A) (irs, 1986) us-
ing the LISS-II sensor that has a resolution of
36.25m×36.25m. The image is contained in four
spectral bands namely, blue band of wavelength 0.45-
0.52 µm, green band of wavelength 0.52-0.59 µm, red
band of wavelength 0.62-0.68 µm, and near infra red
band of wavelength 0.77-0.86 µm. Each band is of
size 512 × 512, i.e., the size of the data set to be clus-
tered in all the bands is 262144.
Fig. 6 shows the IRS image of a part of Bombay in
the near infrared band. As can be seen, the city area is
enclosed on three sides by the Arabian sea. Towards
Figure 7: Clustered IRS image of Bombay using DECC-
ANN technique.
the bottom right of the image, there are many islands,
including the famous Elephanta island. The dockyard
is situated on the south eastern part of Bombay, which
can be seen as a set of three finger like structure. As
per our ground knowledge, these clusters correspond
to 7 landcoverregions namely concrete (Concr.), open
spaces (OS1 and OS2), vegetation (Veg), habitation
(Hab), and turbid water (TW1 and TW2).
The result of the application of the proposed
DECC-ANN technique on the Bombay image is
shown in Fig. 7. The southern part of the city, which
is heavily industrialized, has been classified as pri-
marily belonging to habitation and concrete. Here,
the class habitation represents the regions having
concrete structures and buildings, but with relatively
lower density than the class Concrete. Hence these
two classes share common properties. From the re-
sult, it appears that the large water body of Arabian
sea is grouped into two classes (TW1 and TW2). It is
evident from the figure that the sea water has two dis-
tinct regions with different spectral properties. Hence
the clustering result providing two partitions for this
region is quite expected. Most of the islands, dock-
yard, several road structures have been correctly iden-
tified in the image. As expected, there is a high pro-
portion of open space and vegetation within the is-
lands.
Fig. 8 demonstrates the Bombay image clustered
using the GACC-ANN clustering algorithm. It can be
IMPROVEMENT OF DIFFERENTIAL CRISP CLUSTERING USING ANN CLASSIFIER FOR UNSUPERVISED
PIXEL CLASSIFICATION OF SATELLITE IMAGE
27

Figure 8: Clustered IRS image of Bombay using GACC-
ANN technique.
noted from the figure that the water of the Arabian sea
has been wrongly clustered into three regions, rather
than two as obtained earlier. It appears that the other
regions in the image have been classified more or less
correctly for this data. In Fig. 9, the Bombay image
clustered using K-means clustering has been shown.
It appears from the figure that the sea area is wrongly
classified into four different regions. Also there are
overlapping between the classes turbid water and con-
crete, as well as between open space and vegetation.
Table 5: Average ζ and MS values over 50 runs of different
algorithms for the two Real-life data sets.
Algorithms ζ I
DECC-ANN 3891147.3809 356.5182
GACC-ANN 3891234.7731 322.0861
SACC-ANN 3891361.5029 278.9641
K-means-ANN 3891607.8262 224.6372
DECC 3891206.4133 328.8802
GACC 3891295.8029 306.6037
SACC 3891422.8442 257.0382
K-means 3891791.0749 203.3929
The superiority of the DECC-ANN technique
can also be verified from the I index values that
are reported in Table 5. The ζ and I index val-
ues for DECC-ANN are tabulated along with other
algorithms. From the table, it is found for I
index that these values are 356.5182, 322.0861,
278.9641, 224.6372, 328.8802, 306.6037, 257.0382
and 203.3929, respectively. As a higher value of I
index indicates better clustering result, it follows that
DECC-ANN outperforms over the other algorithms.
Figure 9: Clustered IRS image of Bombay using K-means
algorithm.
7 CONCLUSIONS
This article proposes a newly developed integrated
clustering technique. The developed technique in-
tegrates differential evolution based crisp clustering
with ANN classifier. The differential evolution based
crisp clustering technique minimize the intra cluster
compactness ζ for finding the proper partitions. Af-
ter that, the ANN classifier is used to train by the
fraction of data points, selected based on their prox-
imity to the respective centres. Finally, remaining
points are thereafter classified by the trained classi-
fier. For demonstrating the superiority of the tech-
nique, its performance has been compared with those
of genetic algorithm based crisp clustering, simulated
annealing based crisp clustering and K-means for two
synthetic and two real life data sets. It’s integrated
version has also been tested. Statistical significance
test based on Wilcoxon’s rank sum test has been con-
ducted to judge the statistical significance of the clus-
tering solutions produced by different algorithms. In
this context, IRS satellite image of Mumbai has been
classified using the proposed technique and compared
with other clustering algorithms. The results indicate
that the newly developed DECC-ANN technique can
be efficiently used for clustering different data sets.
As a scope of further research, performance of other
popular classifiers can be tested. The work can also
be extended to solve clustering problems where the
number of clusters is not known a priori. Finally, ap-
plication of DECC-ANN to several real life domains
e.g., VLSI system design, data mining and web min-
ing, needs to be demonstrated. The authors are cur-
rently working in this direction.
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
28

ACKNOWLEDGEMENTS
This work was also supported by the Polish Ministry
of Education and Science (grants N301 159735, N518
409238, and others).
REFERENCES
(1986). IRS data users handbook. NRSA, Hyderabad, In-
dia.
Andersen, L. N., Larsen, J., Hansen, L. K., and HintzMad-
sen, M. (1997). Adaptive regularization of neural clas-
sifiers. In. Proc. of the IEEE workshop on neural net-
works for signal processing VII, NewYork, USA, pages
24–33.
Bishop, C. (1996). Neural Networks for Pattern Recogni-
tion. Oxford University Press.
Everitt, B. S. (1993). Cluster Analysis. Halsted Press, Third
edition.
Goldberg, D. E. (1989). Genetic Algorithms in Search, Op-
timization and Machine Learning. Addison-Wesley,
New York.
Hollander, M. and Wolfe, D. A. (1999). Nonparametric
Statistical Methods. 2nd ed.
Jain, A. K. and Dubes, R. C. (1988). Algorithms for Clus-
tering Data. Prentice-Hall, Englewood Cliffs, NJ.
Jain, A. K., Murty, M. N., and Flynn, P. J. (1999). Data
clustering: A review, volume 31.
Jardine, N. and Sibson, R. (1971). Mathematical Taxonomy.
John Wiley and Sons.
Kirkpatrik, S., Gelatt, C. D., and Vecchi, M. P. (1983). Op-
timization by simulated annealing. Science, 220:671–
680.
Laprade, R. H. (1988). Split-and-merge segmentation of
aerial photographs. Computer Vision Graphics and
Image Processing, 48:77–86.
MacKay, D. J. C. (1992). The evidence framework ap-
plied to classification networks. Neural Computation,
4:720–736.
Maulik, U. and Bandyopadhyay, S. (2002). Performance
evaluation of some clustering algorithms and validity
indices. IEEE Transactions on Pattern Analysis and
Machine Intelligence, 24(12):1650–1654.
Sigurdsson, S., Larsen, J., and Hansen, L. (2002). Out-
lier estimation and detection: application to skin le-
sion classification. In Proc. Int. conf. on acoustics,
speech and signal processing.
Storn, R. and Price, K. (1995). Differential evolution - A
simple and efficient adaptive scheme for global op-
timization over continuous spaces. Technical Report
TR-95-012, International Computer Science Institute,
Berkley (1995).
Storn, R. and Price, K. (1997). Differential evolution - A
simple and efficient heuristic strategy for global opti-
mization over continuous spaces. Journal of Global
Optimization, 11:341–359.
van Laarhoven, P. J. M. and Aarts, E. H. L. (1987). Sim-
ulated Annealing: Theory and Applications. Kluwer
Academic Publisher.
Wong, Y. F. and Posner, E. C. (1993). A new clustering
algorithm applicable to polarimetric and sar images.
IEEE Transactions on Geoscience and Remote Sens-
ing, 31(3):634–644.
IMPROVEMENT OF DIFFERENTIAL CRISP CLUSTERING USING ANN CLASSIFIER FOR UNSUPERVISED
PIXEL CLASSIFICATION OF SATELLITE IMAGE
29
